关于第一类曲面积分的计算方法和技巧

王 静,李应岐,方晓峰

(第二炮兵工程大学理学院,西安 710025)

关于第一类曲面积分的计算方法和技巧

王 静,李应岐,方晓峰

(第二炮兵工程大学理学院,西安 710025)

针对第一类曲面积分的计算这一难点,结合例题,讨论了将其转化为二重积分时需要注意的问题,并给出了通过选取不同微元转化为其他类型积分的一些方法以及常用的技巧.

第一类曲面积分;微元;计算方法

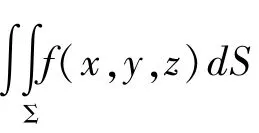
1 计算时需要注意的问题

对于第一类曲面积分,基本的计算方法是转化为投影区域上的二重积分,可概括为:“一投、二代、三换”[1].在这个过程中,学生容易出错的地方是“投影”.事实上,积分域向哪个坐标面投影,主要取决于积分曲面的方程.要保证向某坐标面投影时,曲面的方程可以写成显式、单值函数.换句话说,曲面上的点与投影区域上的点要保持一一对应.

有人说,Σ在xoy面上的投影是圆周,面积为零,所以I=0.

此说法是错误的,按第一类曲面积分一般计算方法,若要投影到xoy平面上,曲面方程必须可以写成z=z(x,y)的表达式,而本题中圆柱面的方程不能表达成z=z(x,y)的形式,因此把Σ在xoy面上投影来计算是得不到结果的.

正确的做法是:选取圆柱面Σ向yoz面或xoz面上投影,如果投影到yoz面上,那么得到投影区域为: Dyz:-a≤y≤a,0≤z≤h,圆柱面方程可表示成,从而

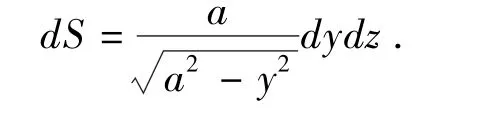
又因对称性,只要在Σ上x≥0的那部分曲面Σ1上积分值乘以2倍即可:

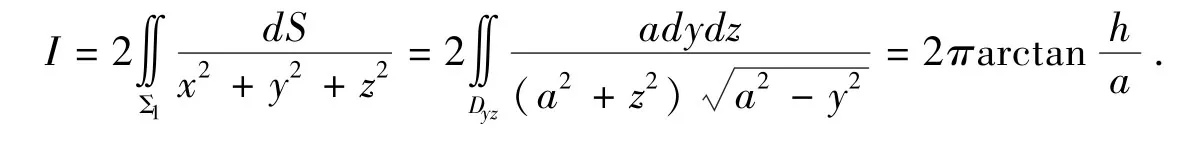
所以向坐标面投影时,一定要注意:

(1)曲面在坐标面上的投影区域的面积不能为0;

(2)z=z(x,y)必须为单值函数,若曲面Σ可表示为单值函数x=x(y,z)或y=y(x,z)也可得相应的曲面积分化为二重积分的公式.否则,就要对积分区域分片[2].

同时,从例1看到,有些时候用基本计算方法来计算该类积分是很繁琐的.事实上,除了把第一类曲面积分转化为二重积分以外,还可以通过取不同的微元,转化为其他类型的积分.

2 选择适当的微元计算第一类曲面积分

(1)转化为定积分.如果被积函数为一元函数,比如f(z),则可以考虑将曲面元化为积分元dS= h(z)dz,假设积分曲面夹在两平面z=a和z=b之间,那么

(2)转化为曲线积分[3].如果被积函数是二元函数,比如f(x,y),而积分曲面向xoy面的投影是一条平面曲线时,可以考虑将曲面元化为弧微元dS=h(x,y)ds,那么

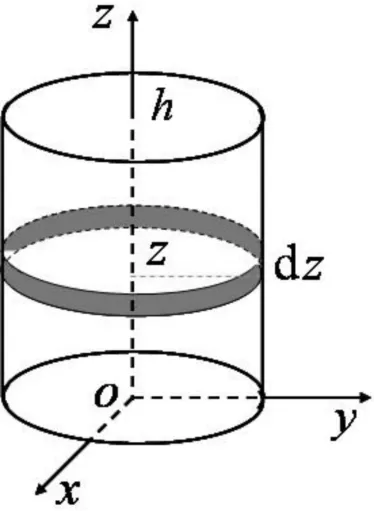
图1

(3)利用球面坐标系计算.如果积分曲面是球面x2+y2+z2=R2或球面的一部分,则可转化到球面坐标系下计算,此时曲面微元为dS= R2sinφdθdφ.

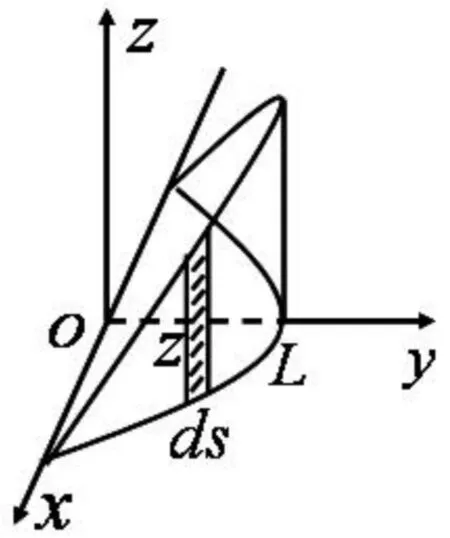
图2

由此可见,第一类曲面积分的计算方法也是灵活多变的,读者要善于思考,选择简便易算的方法来做.

3 常用的计算技巧

(1)利用积分曲面的方程简化被积函数.因为被积函数是定义在积分曲面上的,所以可以先利用曲面方程简化被积函数后再计算.

[1]同济大学应用数学系.高等数学(下)[M].第6版.北京:高等教育出版社,2007.

[2]高等学校工科数学课程教学指导委员会.高等数学释疑解难[M].北京:高等教育出版社,1992.305-306.

[3]吕锋.第一类曲面积分的一种解法[J].高等数学研究,2011,14(2):47-48.

[4]张参燕,王耀革,姚红.一类曲面积分的简单计算与推广[J].高等数学研究,2010,13(2):29-31.

[5]马菊侠,吴云天.高等数学题型归纳·方法点拨·考研辅导[M].北京:国防工业出版社,2010.336-339.

【责任编辑 牛怀岗】

Calculation Methods and Techniques on the First Curved Surface Integral

WANG Jing,LIYing-qi,FANG Xiao-feng
(College of Science,Second Artillery Engineering University,Xi'an 710025,China)

For calculation of the first surface integrals,combined with the example,the paper discusses the need to pay attention to its conversion to double integral problem,and gives somemethod of convert to other types of integral by choose differentmicroelement and the commonly used skills.

first curved surface integral;microelement;calculationmethod

O172.2

A

1009-5128(2014)03-0019-03

2013-10-31

王静(1981—),女,甘肃武威人,第二炮兵工程大学理学院讲师,主要从事代数学研究.