关于四类函数的几个结论

杨明顺

(渭南师范学院数学与信息科学学院,陕西渭南 714099)

关于四类函数的几个结论

杨明顺

(渭南师范学院数学与信息科学学院,陕西渭南 714099)

利用初等及组合方法对连续函数、单调函数、有界变差函数、绝对连续函数的关系进行了探讨,得出了绝对连续函数一定是有界变差函数,单调函数是有界变差函数,绝对连续函数一定是连续函数的结论.

连续函数;单调函数;有界变差函数;绝对连续函数

连续函数、单调函数、有界变差函数、绝对连续函数是函数论中广泛使用的四类函数,搞清楚它们之间的关系对于掌握这些函数很有必要.目前有关研究它们之间关系的完整结果很少看到,本文就此问题进行了探究.

定义1[1]设f(x)是定义在点集E⊂R上的函数,x0∈E,若对∀ε＞0,∃δ＞0,当x∈E∩U(x0, δ)时,有f(x)-f(x0)＜ε,则称f(x)在x0上连续,如果f(x)在E上每点都连续,就称f(x)在E上连续.

定义2[1]设f(x)是定义在实直线R中点集E上的有限函数,如果对任意x1,x2∈E,当x1＜x2时,不等式f(x1)≤f(x2)恒成立,就称f(x)是E上的单调增加函数,如果不等式f(x1)＜f(x2)恒成立,就称f(x)是E上的严格单调增加函数;如果当x1＜x2时,不等式f(x1)≥f(x2)恒成立,就称f(x)是E上的单调减少函数,如果不等式f(x1)＞f(x2)恒成立,就称f(x)是E上的严格单调减少函数.

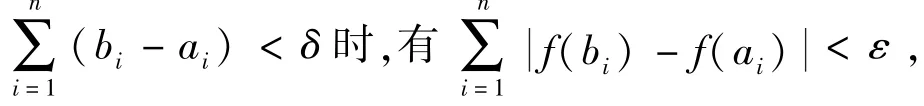
1.绝对连续函数一定是有界变差函数

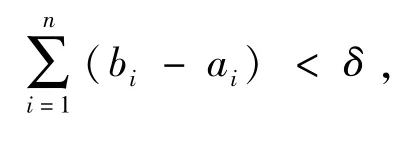
2.单调函数是有界变差函数

3.绝对连续函数一定是连续函数

4.连续函数不一定是有界变差函数

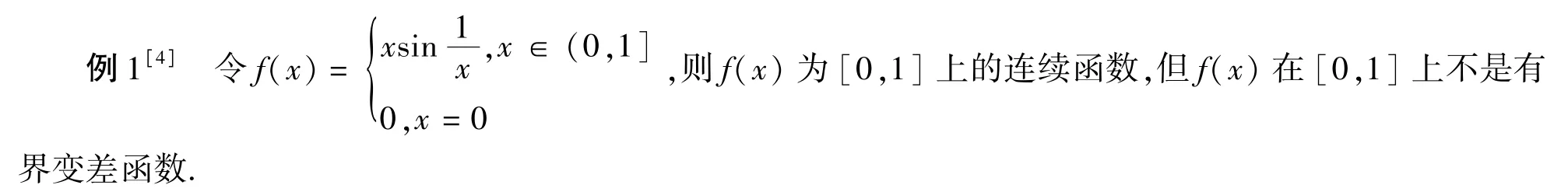
5.有界变差函数不一定是连续函数

6.有界变差函数不一定是绝对连续函数

7.有界变差函数不一定是单调函数

例4 设f(x)=x,g(x)=x2,在[0,1]上都单调增加,令:H(x)=f(x)-g(x),x∈[0,1],则H(x)在[0,1]上有界变差函数,但H(x)在[0,1]上不是单调函数.

8.绝对连续函数不一定是单调函数

绝对连续函数一定是有界变差函数,而有界变差函数不一定是单调函数,从而可知:绝对连续函数不一定是单调函数.

9.单调函数不一定是绝对连续函数

10.单调函数不一定是连续函数

11.连续函数不一定是单调函数

例7 设f(x)=x2,则f(x)在定义域(-∞,+∞)内是连续的,但不是单调函数.

12.连续函数不一定是绝对连续函数

[1]赵静辉,徐吉华.实变函数简明教程(函数论部分)[M].武汉:华中科技大学出版社,1996.86-96.

[2]胡适耕.实变函数(微分论部分)[M].北京:高等教育出版社,1997.153-160.

[3]张晓岚.实变函数与泛函分析简明教程[M].北京:高等教育出版社,2000.65-75.

[4]张喜堂.实变函数论的典型问题与方法[M].武汉:华中师范大学出版社,2000.307-320.

[5]胡长松.实变函数(有界变差函数)[M].北京:科学出版社,2002.133-134.

【责任编辑 牛怀岗】

On Several Conclusions about Four Kinds of Functions

YANG Ming-shun
(School of Mathematics and Information Science,Weinan Normal University,Weinan 714099,China)

The paper,based on the elementary function and the combinatorialmethod,discussed the relation between the continuous function,themonotonic function,the bounded variation function and the definitely continuous function.It proved that the absolute continuous functionmust be the bounded variation function,monotone function is a function of bounded variation,and absolutely continuous function is a continuous function.

continuous function;monotonic function;bounded variation function;definitely continuous function

O156.4

A

1009-5128(2014)03-0016-03

2013-09-30

陕西省教育厅科学研究计划(自然科学专项)项目:关于F.Smarandache数论问题的计算机辅助研究(2013JK1165);渭南师范学院教改项目:大学数学教学改革的探索与实践(JG201345)

杨明顺(1964—),男,陕西渭南人,渭南师范学院数学与信息科学学院教授,主要从事数论研究.