横风环境中弓网动力学性能分析
李瑞平,周 宁,吕青松,张卫华,梅桂明
(西南交通大学牵引动力国家重点实验室,成都 610031)
横风环境中弓网动力学性能分析
李瑞平,周 宁,吕青松,张卫华,梅桂明
(西南交通大学牵引动力国家重点实验室,成都 610031)
为研究横风对弓网动力学性能的影响,基于AR模型的线性滤波法和Davenport风速谱,构建了受电弓-接触网系统的随机风场,获得了作用于受电弓和接触网的风速时程;建立受电弓/高速列车空气动力学仿真模型,采用计算流体力学方法求解了列车运行速度为300 km·h-1,不同横风速度下的受电弓气动抬升力,从而得到横风平均速度为20 m·s-1时,受电弓气动抬升力时程;采用三维弓网耦合动力学模型,系统分析了横风对弓网动力学的影响规律。研究表明,横风使得受电弓的气动抬升力变大,并与横风速度的平方成正比;受电弓气动抬升力的增加和波动,使得接触压力平均值以及标准差变大;接触网产生的风致振动改变了弓网之间的接触状态,导致接触压力波动范围变大,因此,列车在横风环境中运行时,不仅增大了弓网接触压力从而加剧了受电弓滑板和接触线的磨耗,而且使得接触压力最小值减小以及标准差增大,导致弓网受流质量显著降低。
受电弓;接触网;耦合动力学;横风;接触压力
高速列车通常采用电力牵引,列车运行过程中所需电能通过受电弓-接触网系统提供。受电弓安装于列车顶部属于移动设备,接触网架设在铁路沿线属于固定设备,受电弓与接触网在相对滑动接触过程中实现电能的传输,弓网之间必须具备可靠的接触才能保证电能传输的不间断。然而,列车高速运行时,弓网相互作用形成了耦合的振动系统,弓网系统的动力学性能成为决定受流质量的关键因素,因此,诸多学者[1-2]对弓网系统动力学仿真以及试验方法[3-4]开展了广泛而深入的研究,为弓网系统的稳定受流提供了重要的技术支撑作用。
受电弓的空气动力学性能是限制列车运行速度提高的关键因素之一,研究表明高速气流作用于受电弓形成的气动力对弓网动力学和受流质量具有重要影响[5-6]。这是由于受电弓的静态抬升力通常为70 N左右,气动力使得受电弓抬升力产生了较大变化,从而改变弓网之间的动态接触压力,因此,高速列车所用受电弓通常会安装导流板,利用导流板产生的气动升力调节受电弓的抬升力,从而确保高速列车以不同速度和方向运行时,受电弓都具备合理的抬升力。欧洲铁路联盟认为不仅要考虑列车运行时产生的高速气流对弓网受流的影响,同时也要关注横风的影响[7]。Pombo等[8]研究指出横向自然风作用于接触网引起的弓网动力学性能的变化可以忽略,只需考虑横风环境中受电弓抬升力变化引起的弓网受流质量的改变,然而,研究过程中受电弓气动抬升力是通过风洞试验获得,并未考虑横向自然风的时空相关性以及列车对受电弓所在流场的影响。国内进行了横向自然风作用下接触网的风振响应以及对弓网受流的影响分析,指出接触网在横向自然风作用下表现出横向和垂向的耦合振动[9],实验结果证实接触网风振对弓网动态性能具有很大影响[10],但是,列车在横风环境中运行时,受电弓与接触网同时受到横风的影响,不考虑横风引起的受电弓气动力变化,则难以准确分析和评估横风对弓网受流质量的影响。
本文基于Davenport风速谱和线性滤波法,建立了受电弓-接触网系统的随机风场,得到了作用于接触网和受电弓不同时刻的横风风速。采用计算流体力学方法获得了接触网的风荷载以及受电弓的气动抬升力,并且拟合了不同横风风速条件下受电弓气动抬升力计算公式,从而获得列车在横风环境中运行时,受电弓气动抬升力时程曲线。采用三维弓网耦合动力学仿真模型,系统分析了横向自然风作用于受电弓-接触网系统时,弓网动力学性能的变化规律,从而为高速列车在横风环境中运行的安全性评估和大风预警系统的建立,提供了准确的理论方法和重要的基础数据。
1 受电弓-接触网系统随机风场
1.1 脉动风模拟
自然风包含周期较长的平均风和周期较短的脉动风,平均风周期一般大于结构的自振周期,通常认为平均风荷载对结构产生静力作用;而脉动风周期一般在几秒至几十秒,脉动风荷载的作用性质可视为动载荷。接触网属于柔性结构,其自重较轻,自振频率较低,属风敏感结构,在风荷载作用下易产生较大的变形和振动,且表现出很强的非线性特征[9];此外,受电弓在自然风作用下产生的非定常气动力,会导致受电弓抬升力变化以及产生风致振动,从而使得弓网接触压力发生显著改变。因此,需要建立受电弓-接触网系统的随机风场,从而考虑自然风的脉动成分,才能准确获得列车在横风环境中运行时,弓网相互作用的动态行为。任一点处的自然风风速可表示为
式中:x,y,z为该点的空间坐标,t为时间;W(x,y,z,t)为该点的自然风风速,W(z)为该点高度z时的平均风速,w(x,y,z,t)为该点的脉动风速。
平均风速沿高度变化的规律可用指数律来表示,因此,平均风速W与10 m高度处的平均风速的指数律关系为

大气风脉动可近似认为是各态历经、零均值、平稳高斯过程,其模拟方法主要有谐波合成法、线性滤波法和小波变换法,其中,线性滤波法可模拟具有随机性、时间和空间相关性的脉动风场,并且具备高效、高精度的特点[11]。此外,考虑到高速铁路所用接触网,接触线离轨面高度通常为5 300mm左右,而接触网结构高度为1 500mm左右,可忽略弓网系统各模拟点处因高度变化引起的风速差异,因此,本文采用湍流尺度沿高度不变的Davenport谱和基于AR模型的线性滤波法建立受电弓-接触网系统的随机风场。
Davenport风速谱可表示为[12]


1.2 随机风场建立
本文针对武广高速铁路接触网和高速列车建立随机风场,接触网跨距为50 m,以长度500 m的接触网为研究对象。沿接触网布置方向,将接触网和高速列车所在区域分割成间距为25 m的等分区,在等分区两侧分别取风速模拟点,从而建立受电弓-接触网系统的随机风场,如图1所示。等分区内的风速与左侧模拟点的风速一致,接触线和承力索上的风速与等分区内的风速相同,作用于受电弓的风速则根据其所在位置而确定,若受电弓位于一个等分区则取该等分区的风速,若同时位于两个等分区则风速取两者的平均值。

图1 受电弓-接触网系统随机风场Fig.1 Stochastic wind field of pantograph-catenary system
采用四阶AR模型的线性滤波法,地面粗糙度系数取0.16,模拟点高度取5 300mm,时间步长取0.1 s,编制了MATLAB计算程序。图2(a)给出了平均风速为20 m·s-1时,点10处的脉动风速时程,为验证模拟得到的脉动风速时程的准确性,将脉动风速时程变换到频域中,在双对数坐标系中与目标谱进行比较,发现模拟谱和目标谱比较一致,见图2(b),由此便可建立受电弓-接触网系统的随机风场,研究高速列车在横风环境中运行时的弓网动力学特性。

图2点10模拟脉动风速时程及功率谱比较(W10=20 m·s-1)Fig.2Wind speed time series and power spectrum comparison of point10(W10=20 m·s-1)
2 受电弓-接触网系统气动载荷
2.1 受电弓气动载荷
列车在横风环境中高速运行时,一方面受到与列车运行方向相反,速度为-V的高速气流作用;另一方面受到速度为W的横风作用,高速气流与横风的合成风速度为U,列车运行速度与合成风速度之间的夹角β称为侧偏角,如图3所示。受电弓在高速气流作用下,使其抬升力产生显著变化进而影响弓网之间的接触压力和受流质量,而横风会使受电弓产生横向气动载荷,同时受电弓处于列车空气绕流场之中,横风也会改变受电弓周围的流场分布进而影响受电弓抬升力。文献[14]指出受电弓在横风作用下产生的横向位移较小,可不予考虑,因此,受电弓在高速气流和横风共同作用时,只需考虑受电弓在两者作用下引起的抬升力变化对弓网动力学性能的影响。

图3 合成风速度Fig.3 Combined wind velocity
受电弓气动抬升力可通过线路试验、风洞试验以及数值仿真获得,线路试验的精确度高,但受气候条件的限制,要获得不同横风条件下的受电弓气动抬力数据十分困难。风洞试验能够完成全尺寸的单个受电弓空气动力学试验,但是横风环境中受电弓周围流场受到列车车体的影响,气流速度的大小和方向均会发生变化,所以必需采用包含受电弓的高速列车缩比模型进行风洞试验,缩比模型的风洞试验难以保证与列车实际流场中的雷诺数一致,从而导致受电弓气动力测量产生较大误差[14]。高性能计算机和计算流体力学的发展,使得列车空气动力学数值仿真成为了分析列车周围流场和优化列车空气动力学性能的关键手段之一[15]。因此,本文采用数值仿真进行横风条件下受电弓气动力的计算,建立受电弓/高速列车三维空气动力学仿真模型,如图4所示,受电弓主要由弓头、框架和底座三部分构成,并且受电弓周围存在较多高压电器元件。采用计算流体商用软件FLUENT,计算了列车在横风环境中运行时受电弓所受气动力,边界条件设置、计算区域和网格,如图5所示,列车和受电弓表面设置为无滑移壁面边界;地面设置为以列车速度滑移的壁面边界;计算区域顶部设置为对称边界。

图4 受电弓/高速列车空气动力学模型Fig.4 Aerodynamic model of pantograph/high speed train

图5 计算区域和网格Fig.5 Computational domain and grid
高速列车周围流场采用定常不可压缩流描述,湍流模型采用标准的κ-ε模型,计算了列车运行速度为300 km·h-1,不同横风风速(0~40 m·s-1)时,受电弓各部件的气动力。根据受电弓气动抬升力计算方法[16],获得了不同横风风速条件下,受电弓产生的气动抬升力,如图6所示,由图可知,列车运行过程中产生的高速气流使得受电弓产生了较大的气动抬升力,当横风速度为0时,气动抬升力大小为65 N左右;随着横风速度的增加,气动抬升力产生了显著的增加,且与横风速度的平方成正比,图6中曲线根据多项式拟合获得,拟合关系式为
Fal=0.045 96W2+0.328 44 W+65.930 61(5)式中:Fal为受电弓气动抬升力;W为横向自然风风速。

图6 不同横风速度下气动抬升力Fig.6 Aerodynamic up lift force with different crosswind speeds
对于横风作用下列车气动力的计算,传统准定常法只考虑瞬态湍流产生的脉动特性,忽略了湍流的非定常记忆影响,即气动力的波动与气流的波动相一致,不存在任何滞后和衰减。但是,准定常理论容易产生较大误差,而通过列车空气动力学导纳函数和权重函数,则可建立列车气动力波动和随机风速波动的关系[17]。然而,受电弓与接触网在气流作用下形成的湍流长度尺度与高速列车相比存在较大差别,因此,可认为作用于受电弓和接触网的气动力波动与随机风的波动相一致[14]。根据受电弓-接触网的随机风场,可获得列车不同运行时刻作用于受电弓的自然风风速,然后,根据式(5)便可计算受电弓在随机风作用下的气动抬升力。当列车运行速度为300 km·h-1,横向自然风平均速度为20 m·s-1时,受电弓气动抬升力时程,如图7所示,由图可知,横向自然风作用于受电弓时,受电弓的气动抬升力产生显著增加并且随时间变化存在较大的波动性。

图7 气动抬升力时程Fig.7 Aerodynamic uplift force time series
2.2 接触网气动载荷
根据模拟点风速时程以及接触线和承力索截面尺寸,计算作用于接触线和承力索上的风荷载,其中,基本风压和线索的风荷载体型系数采用《铁路电力牵引供电设计规范》(TB10009-2005)规定值,则有
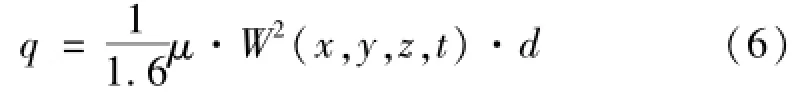
式中:q为线索单位长度风荷载(N·m-1);μ为线索体型系数;W(x,y,z,t)为风速(m·s-1);d为线索截面高度(m)。
3 弓网耦合动力学模型
受电弓与接触网相互作用过程中,弓网之间的垂向耦合振动对受流质量具有重要影响,因此,传统的弓网耦合动力学仿真模型通常只考虑垂向的接触行为。然而,接触网受横向自然风作用时,接触线表现为垂向和横向的耦合振动,垂向振动位移可认为是风载荷引起的接触线导高不平顺,这种不平顺不仅会影响弓网的垂向振动行为,而且会使得受电弓滑板和接触线产生纵向的冲击。接触线横向振动会改变弓网之间的横向作用力,从而引起弓网系统产生横向的异常振动,这对接触网支持装置以及受电弓结构的强度产生不利影响,因此,本文进行横风条件下的弓网耦合动力学仿真时,采用了考虑弓网接触形貌的三维耦合动力学模型。接触网模型如图8所示,其拉出值为300 mm,主要包含接触线、承力索、辅助承力索和吊弦,其中,承力索、辅助线和接触线采用梁单元进行模拟,吊弦采用弹簧质量单元模拟;高速铁路接触网通常采用全补偿链型悬挂,接触线和承力索两端均设有补偿装置,可认为两者的张力是恒定值,因此,进行接触线和承力索边界条件处理时,在其垂向和横向施加位移约束而纵向施加张力,接触网材料参数如表1所示。列车在横风环境中运行时,考虑到接触线和受电弓滑板存在较大的相对运动,为准确描述弓网之间的接触行为,将弓头滑板考虑为柔性体;此外,弓网相互作用过程中,上框架会产生弹性变形且对弓网的接触状态产生较大影响,因此,将上框架同样考虑为柔性体,弓头与上框架之间通过弹簧单元相连;受电弓下臂杆刚度较大,而拉杆仅承受拉力,为此,将下臂杆和拉杆均考虑为刚性体[18],受电弓模型如图9所示。

图8 三维接触网模型Fig.8 Three dimensional catenarymodel

图9 刚柔混合受电弓模型Fig.9 Rigid-flexible hybrid pantograph model

表1 接触网材料参数Tab.1 Material parameters of the catenary
4 横风对弓网系统影响
为研究横风对弓网动力学性能的影响,需系统分析横风引起的接触网振动以及受电弓气动力变化对弓网接触压力的影响,因此,本文建立四种工况详细讨论了弓网系统在横风作用下,接触压力的变化规律。工况1:不考虑横风对受电弓和接触网的影响;工况2:考虑横风对受电弓的影响,不考虑横风对接触网的影响;工况3:考虑横风对接触网的影响,不考虑横风对受电弓的影响;工况4:考虑横风对受电弓-接触网系统的影响。
列车运行速度为300 km/h,横向自然风的平均风速为20 m·s-1时,四种工况下计算得到的弓网接触压力,如图10(a)~图10(c)所示,接触压力统计值,如表2所示。考虑到边界条件对计算结果的影响,文中选取了50m~450m处的计算结果进行统计和分析。

表2 接触压力统计参数Tab.2 Contact force statistical parameters

图10 弓网接触压力Fig.10 Contact forces between pantograph and catenary
由图10(a)可知,当列车在无横风环境中运行时,弓网接触压力的变化在每个跨距内具有一定的规律性,这是由于接触网弹性随跨距周期性变化而产生的。当仅考虑横风作用于受电弓时,接触压力变化的规律性没有明显改变,但是相比不考虑横风作用时,接触压力的平均值、最大值和标准差表现出明显的增加,由表2中的接触压力统计结果可知,平均值、最大值和标准差分别增加了12.37%、10.42%和21.58%。因此,横风引起的受电弓气动抬升力的增加以及波动性,导致了接触压力的平均值、最大值以及标准差相应增加,接触压力的增加会使接触网定位器处的抬升量加大,若抬升量超出接触网的设计值则会产生撞弓事故,同时也会加剧受电弓滑板和接触线的磨耗从而增加运营成本。
由图10(b)可知,当仅考虑横风作用于接触网时,接触压力的波动范围显著增加,虽然,接触压力的平均值未表现出明显变化,但是相比无横风作用时,接触压力的最大值和标准差分别增加了3.83%和36.53%;同时接触压力的最小值减小至0从而产生弓网离线,接触压力最大值和标准差的增加表明弓网间的振动加剧,而离线会使得弓网间产生电弧,从而烧蚀接触线和受电弓滑板并且增加受电弓与接触网的电气磨损,由此可知,横风引起的接触网振动改变了弓网之间的接触状态,导致弓网受流质量显著降低。
由图10(c)可知,当横风作用于整个弓网系统时,与其他三种工况相比,不仅接触压力的平均值达到了最大值155.39 N,而且接触压力标准差同样达到了最大值61.67 N,最小值则降低到了0 N。由此可知,虽然,受电弓气动抬升力的增加会提高接触压力的平均值,但是,未能改善接触网风振引起的弓网受流质量恶化的状况。因此,列车在横风环境中运行时,一方面导致弓网接触压力平均值的增加,从而增加了接触线的抬升位移并且加剧了受电弓滑板和接触线的磨耗;另一方面导致接触压力的波动范围变大,由接触压力的最小值和标准差可知,弓网系统在横风作用下受流质量显著降低。
5 结 论
(1)横风作用于受电弓时,受电弓气动抬升力产生了显著增加,并与横风速度的平方成正比,相比不考虑横风作用时,接触压力变化的规律性没有明显改变,但是,接触压力的平均值、最大值和标准差分别增加了12.37%、10.42%和21.58%。
(2)横风作用于接触网时,接触线产生垂向和横向的耦合振动,改变了弓网之间的接触状态,使得接触压力的波动范围增加,相比不考虑横风作用时,接触压力的平均值未表现出明显变化,但是,最大值和标准差分别增加了3.83%和36.53%,并且接触压力最小值降低至0 N,使得弓网间产生了离线。
(3)列车在横风环境中运行时,一方面导致弓网接触压力平均值的增加,从而增加了接触线的抬升位移并且加剧了受电弓滑板和接触线的磨耗;另一方面导致接触压力的波动范围变大,由接触压力的最小值和标准差可知,弓网系统在横风作用下受流质量显著降低。
[1]Wu TX,Brennan MJ.Basic analytical study of pantographcatenary system dynamics[J].Vehicle System Dynamics,1998,30(6):443-456.
[2]Collina A,Bruni S.Numerical simulation of pantographoverhead equipment interaction[J].Vehicle System Dynamics,2002,38(4):261-291.
[3]ZhangWH,MeiG M,Wu X J,et al.Hybrid simulation of dynamics for the pantograph-catenary system[J].Vehicle System Dynamics,2002,38(6):393-414.
[4]Kerstin S,Wolfgang E,Michael K,et al.An approach to continuous on-site monitoring of contact forces in current collectors by a fiber optic sensing system[J].Optics and Lasers in Engineering,2013(51):172-179.
[5]Bocciolone M,Resta F,Rocchi D,et al.Pantograph aerodynamic effects on the pantograph-catenary interaction[J].Vehicle System Dynamics,2006,44(suppl):560-570.
[6]李瑞平,周宁,张卫华,等.高速列车过隧道对弓网动力学影响分析[J].振动与冲击,2013,32(6):33-37.
LIRui-ping,ZHOU Ning,ZHANGWei-hua,et al.Influence of high-speed trains passing through tunnel on pantographcatenary dynamic behaviors[J].Journal of Vibration and Shock,2013,32(6):33-37.
[7]Poetsch G,Evans J,Meisinger R,et al.Pantograph/catenary dynamics and control[J].Vehicle System Dynamics,1997,28(2-3):393-414.
[8]Pombo J,Ambrósio J,Pereira M,et al.Influence of the aerodynamic forces on the pantograph-catenary system for high speed trains[J].Vehicle System Dynamics,2009,47(11):1327-1347.
[9]李瑞平,周宁,张卫华,等.基于AR模型的接触网脉动风场与风振响应[J].交通运输工程学报,2013,13(4):56-62.
LI Rui-ping,ZHOU Ning,ZHANG Wei-hua,et al.Fluctuating wind field and wind-induced vibration response of catenary based on AR model[J].Journal of Traffic and Transportation Engineering,2013,13(4):56-62.
[10]赵飞,刘志刚,韩志伟.随机风场对弓网系统动态性能影响研究[J].铁道学报,2012,34(10):36-42.
ZHAO Fei,LIU Zhi-gang,HAN Zhi-wei.Simulation study on influence of stochastic wind field to dynamic behavior of pantograph-catenary system[J].Journal of the China Railway Society,2012,34(10):36-42.
[11]张希黔,葛勇,严春风,等.脉动风场模拟技术的研究与进展[J].地震工程与工程振动,2008,28(6):206-212.
ZHANG Xi-qian,GE Yong,YAN Chun-feng,et al.Advances in research of simulation technology of fluctuation wind loading[J].Journal of Earthquake Engineering and Engineering Vibration,2008,28(6):206-212.
[12]王之宏.风荷载的模拟研究[J].建筑结构学报,1994,15(1):44-52.WANG Zhi-hong.Simulation of wind loading[J].Journal of Building Structures,1994,15(1):44-52.
[13]舒新玲,周岱.风速时程AR模型及其快速实现[J].空间结构,2003,9(4):27-32.
SHU Xin-Ling,ZHOU Dai.AR model of wind speed time series and its rapid implementation[J].Spatial Structures,2003,9(4):27-32.
[14]Bouferrouk A,Baker C,Sterling M,etal.Calculation of the cross wind displacement of pantographs[C].6th International Colloquium on Bluff Bodies Aerodynamics and Applications,Milano,Italy,2008.
[15]田红旗.中国列车空气动力学研究进展[J].交通运输工程学报,2006,6(1):1-9.
TIAN Hong-qi.Study evolvement of train aerodynamics in China[J].Journal of Traffic and Transportation Engineering,2006,6(1):1-9.
[16]李瑞平,周宁,张卫华,等.受电弓气动抬升力计算方法与分析[J].铁道学报,2012,34(8):26-32.
LI Rui-ping,ZHOU Ning,ZHANG Wei-hua,et al.Calculation and analysis of pantograph aerodynamic uplift force[J].Journal of The China Railway Society,2012,34(8):26-32.
[17]Baker C J.The simulation of unsteady aerodynamic cross wind forces on trains[J].Journal of Wind Engineering and Industrial Aerodynamics,2010,98(2):88-99.
[18]李丰良,李敏,唐建湘.受电弓的建模与参数测试[J].中南大学学报(自然科学版),2006,37(1):194-199.
LIFeng-liang,LIMin,TANG Jian-xiang.Establishment of the pantographsmechanicalmodels and measurement of their parameters[J].Journal of Central South University(Science and Technology),2006,37(1):194-199.
Pantograph-catenary dynamic behavior under crosswind
LIRui-ping,ZHOU Ning,LÜQing-song,ZHANGWei-hua,MEIGui-ming
(State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China)
In order to study the influence of cross wind on pantograph-catenary dynamic behavior,the stochastic wind field of a pantograph-catenary system was established to obtain thewind speed time histories acting on the pantograph and catenary based on the linear filtering method of AR model and Davenport wind speed spectrum.The aerodynamic model of pantograph/high-speed train was built and the computational fluid dynamicsmethod was used to calculate the aerodynamic uplift forces of the pantograph at different crosswind speedswhile the train running ata speed of300 km/h,then the time history of the aerodynamic uplift force of the pantograph was obtained under the average wind speed of 20 m/s.A three-dimensional pantograph-catenary coupled dynamicmodelwas used to analyze the influence rule of the cross wind on the pantograph-catenary dynamic behavior systematically.The results showed that the aerodynamic uplift force of the pantograph increases due to cross wind and it is proportional to the square of the cross wind speed;moreover,the increase and fluctuation of the pantograph aerodynamic uplift force make the mean and standard deviation of the contact force increase;the contactstatus between the collector strip and the contactwire is changed by thewind-induced vibration of the catenary,it leads to the fluctuation range of the contact force expands;therefore,while the train running in the cross wind environment,not only the contact force increases and the abrasion of the collector strip and the contact wire rises,but also the current collection quality drops because the minimum value of the contact force decreases and its standard deviation increases.
pantograph;catenary;coupled dynamics;crosswind;contact force
U264
A
10.13465/j.cnki.jvs.2014.24.007
国家973计划项目(2011CB711105)
2014-05-15 修改稿收到日期:2014-07-16
李瑞平男,博士生,1983年生
张卫华男,博士,教授,博士生导师,1961年生

