多维二参数Logistic项目反应模型的Gibbs抽样法

付志慧，李 斌

（沈阳师范大学 数学与系统科学学院，沈阳 110034）

0 引 言

项目反应理论在心理与教育测量领域中具有广阔的应用前景［1－2］。它以潜在特质理论为基础，核心内容是研究潜在心理特质和反应行为之间的关系，在此基础上，可以分析出被试潜在心理特质（即能力）与项目特性（难度、区分度等）之间的相互影响。项目反应模型按照能力维度可分为单维和多维。单维项目反应模型假定测验的所有题目只考查同一种潜在特质。但是实际心理过程是非常复杂的，且考试（教育测验）通常考查多个能力。本文主要研究多维二参数Logistic（2PLM）的Gibbs抽样方法。

项目反应理论参数估计方法有4种［4］，条件极大似然估计（CMLE：condition maximum likelihood estimation），边际极大似然估计与EM 算法［4－5］（MMLE／EM：marginal maximum likelihood estimation and an EM algorithm），联合极大似然估计（JMLE：joint maximum likelihood estimation），Bayes估计。CMLE以一种参数已知为条件，即项目参数已知求能力值或能力参数已知求项目值。能力的条件估计适用于抽取题库项目来估计被试能力，若在题库未建立前，项目参数和能力参数皆是未知，CMLE不再适用。Birnbaum提出了联合极大似然估计。JMLE可在一定假设下，转化为项目参数的估计和能力参数的估计。两种估计是一个不断互相校正的过程，反复迭代求取稳定值，可以看成是两步估计的过程。但联合极大似然估计有其固有的缺陷：给定长度测试中（即项目个数是固定的），随着被试人数的增加，能力参数的个数也相应增加，称之伴随参数；不随被试人数增加而增加的项目参数，称之为结构参数；当同时估计能力参数和项目参数时，伴随参数可能不存在充分统计量，因此得出估计不一定满足相合性。消除JLME固有的缺陷只有消除伴随参数的影响。MMLE／EM算法将能力参数边际化，给定能力的先验分布，对能力参数进行积分，从而来消除能力参数，在一般条件下该算法可以收敛，计算比较简单，但它对能力需要进行数值积分近似计算，在能力维数较高时，会给计算带来很大困难［6］。为了提高估计的质量，除了当前样本数据，还可以利用客观信息和经验积累的信息，先验信息的加入，参数估计更加稳定，也更合理和符合实际。Albert（1992）给出了二参数正态卵形的一种Gibbs抽样方法［7］。Sahu（2002）将其推广到三参数正态卵形模型［8］。Van der Linden（2007）针对结合反应时间和反应速度的测验，用对数正态模型来拟合被试的反应时间，用三参数正态卵形IRT模型拟合反应得分，将二者结合后给出了Gibbs抽样方法［9］。本文考虑更为一般的多维2PLM，给出了一种基于增加数据的Gibbs抽样方法，易于求出每个参数的后验分布，从而直接给出参数的Bayes后验估计。

1 模型介绍和先验假设

假定有N个被试，n个项目，yij表示第j个被试对第i个项目的反应，答对取值为1，答错取值为0。令pij表示第j个被试对第i个项目正确反应的概率，我们采用多变量Logistic反应函数，形式为：

其中，i＝1，2，…，n，j＝1，2，…，N，θj＝（θj1，…，θjk，…，θjm）为被试j的能力，各维度能力取值范围均为－∞＜θjk＜∞，j＝1，2，…，N，k＝1，2，…，m；ai＝（ai1，…，aik，…，aim），aik＞0，i＝1，2，…，n，k＝1，2，…，m是由项目i在各维度能力上的载荷aik生成的向量，称为区分度参数；bi＝（bi1，…，bik，…，bim）.－∞＜bik＜∞，i＝1，2，…，n，k＝1，2，…，m，为项目i的难度参数向量；特别地，当m＝1时，模型（1）退化为单维2PLM。

令ζ＝（θ，a，b，σ），其中a＝（aik）n×m，b＝（bik）n×m，且（·）n×m表示n×m矩阵。多维2PLM 下，参数ζ的后验分布为：其中D为比例常数。

2 潜在变量的引入及Gibbs抽样过程

对应于反应数据yij，引入2个相互独立的随机变量uij。其中uij服从均匀分布，uij～Uniform（0，1）。由模型（1）易知，潜变量μij要受到yij取值的约束，令

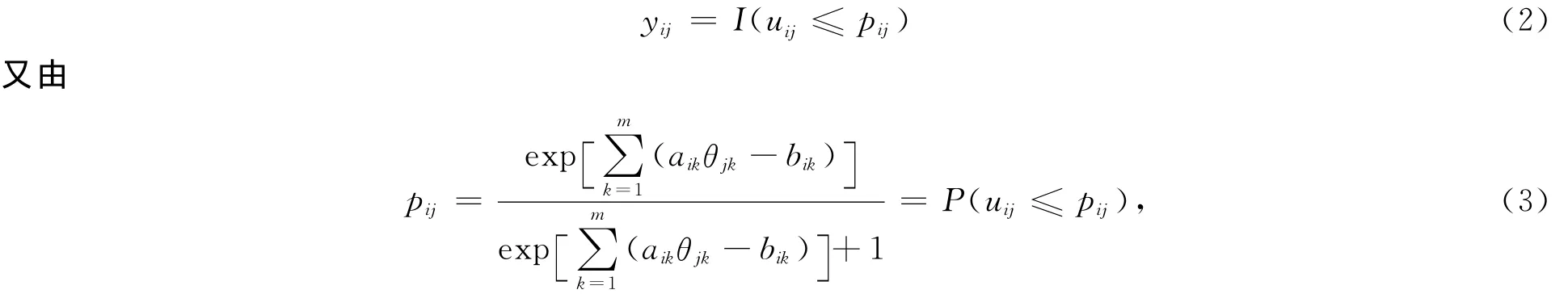
令u＝（uij）n×N，y＝（yij）n×N，随着潜变量u的引入，（ζ，u）的联合后验密度为：

进而，由式（3），有

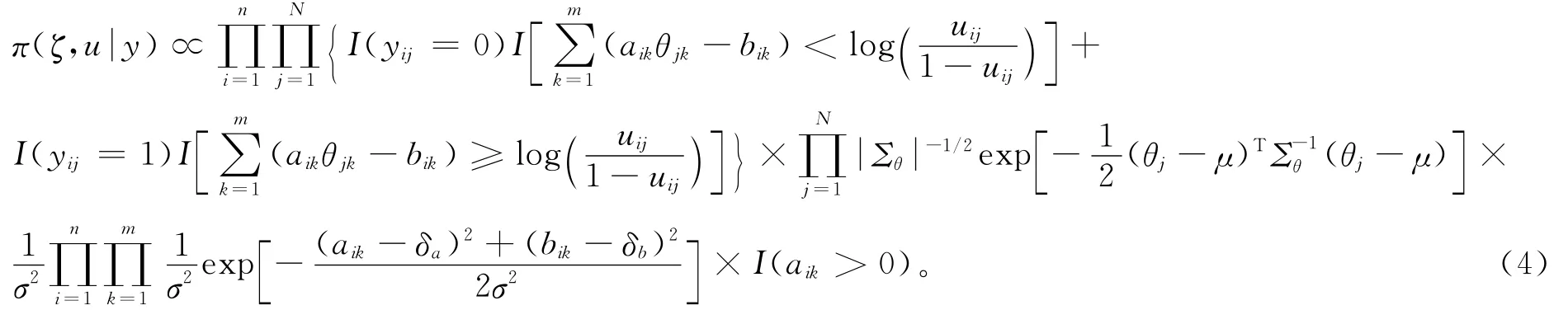
首先，在给定反应数据和其他参数的情形下，抽取uij。在算法的每一步都要满足式（2）。1）uij的满条件分布为

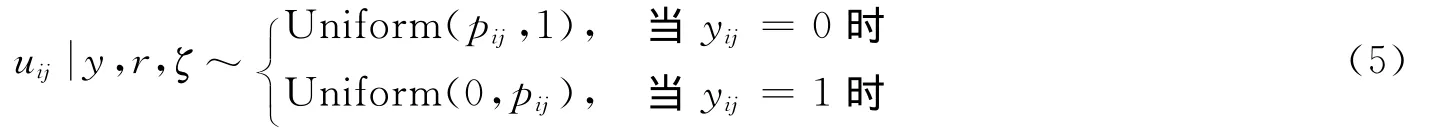
2）给定a，b，σ2的满条件分布为

由式（3），对于任意i，k，令

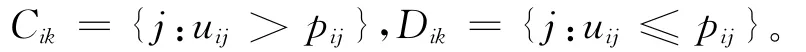
3）则给定其他所有参数和u，r，y，，i＝1，2，…，n，k＝1，2，…，m的满条件分布为

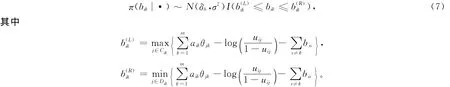
4）同理，θjk，j＝1，2，…，N，k＝1，2，…，.m的满条件分布为

其中，θj（k）是向量θj将第k个元素θjk删除后得到的余向量，即

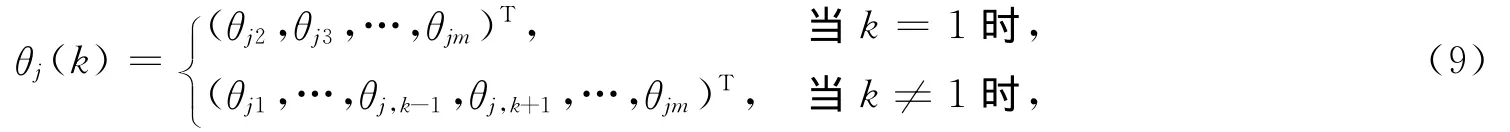
N（vk，）是θjk在给定θj（k）下的条件分布，条件均值和条件方差分别为

（关于vk和的详细计算过程见附录），且

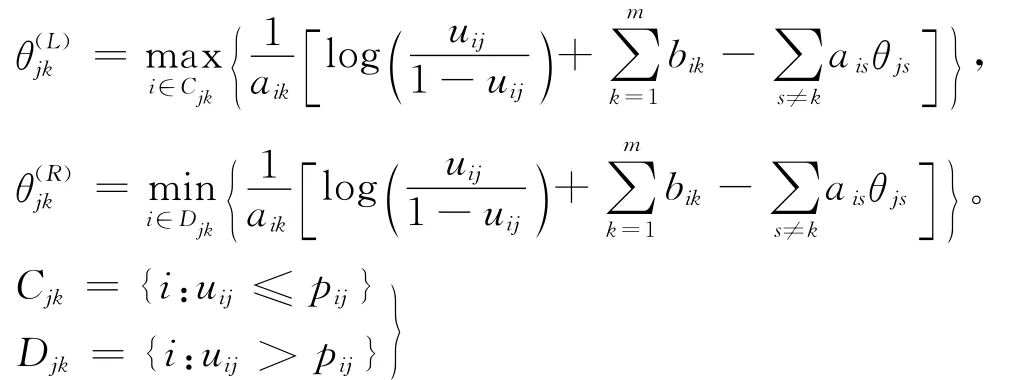
5）给定其他所有参数和u，r，y，aik，i＝1，2，…，n，k＝1，2，…，m的满条件分布为

其中

以下给出了具体的Gibbs抽样步骤（具体程序由Matlab软件编写）。

第1步 从式（5）中抽取u；

第2步 从式（6）中抽取σ2；

第3步 从式（7）中抽取b；

第4步 从式（8）中抽取θ；

第5步 从式（11）中抽取a。

3 结 论

以上讨论了多维二参数LOGISTIC模型的Gibbs抽样问题，采用本文讨论的方法，可简单解决该模型的参数估计问题，这一结果对IRT的发展，对多维项目在测验中的应用是很有意义的，在此基础上，还可以进一步讨论多维项目反应模型的其他问题，如纵向测验［10－11］、多层IRT测验［12］、参数估计优化问题［13－15］等。

附录

条件均值及方差的详细计算过程

若要计算θjk的条件均值vk和条件方差（公式（10）），首先对θj进行置换。令

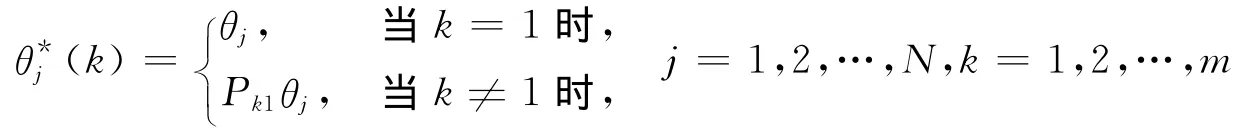
Pk1＝（pst）m×m为置换阵，第（s，t）个元素为

由θj～Nm（μ，Σθ）有（k）～Nm（μ＊（k），（k）），其中

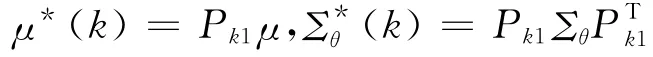
为了求θjk的条件分布，将向量（k）分成两块，因此得：

（μj（k）为θj（k）的数学期望，即μj（k）＝E（θj（k））。且

因此在给定时的条件分布为：

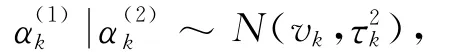
［1］BEAUJEAN A A，STEVEN J O.Using item response theory to assess the flynn effect in the national Longitudinal study of youth 79children and young［J］.Adults Ddata Intell，2008，36（3）：455－463.

［2］CHANG C H，REEVE B B.Item response theory and its applications to patient－reported outcomes measurement［J］.Eval Health Prof，2005，28（3）：264－282.

［3］BAKER F B，KIM S H.Item response theory：parameter Estimation Techniques［M］.2nd Ed.New York：Marcel Dekker，2004.

［4］BOCK R D，AITKIN M.Marginal maximum likelihood estimation of item parameters：An application of an EM－algorithm［J］.Psychometrika，1981，46（3）：443－459.

［5］DAVIER M V，SINHARAY S.An importance sampling EM algorithm for latent regression models［J］.J Educ Behav Stat，2007，32（3）：233－251.

［6］FIEUWS S.High dimensional multivariate mixed models for binary questionnaire data［J］.Appl Stat，2006，55（4）：449－460.

［7］ALBERT J H.Bayesian estimation of normal ogive item response curves using Gibbs Sampling［J］.J Educ Stat，1992，17（3）：251－269.

［8］SAHU S K.Bayesian estimation and model choice in item response models［J］.J Stat Comput and Simul，2002，72（3）：217－232.

［9］LINDEN V D.A hierarchical framework for modeling speed and accuracy on test items［J］.Psychometrika，2007，72（3）：287－308.

［10］JANNEKE M.Application of multidimensional item response theory models to longitudinal data［J］.Educ Psycho Meas，2006，66（1）：5－34.

［11］FU Zhihui，TAO Jian，SHI Ningzhong.Analyzing longitudinal item response data via the pairwise fitting method［J］.Multivariate Behav Res，2011，46（4）：669－690.

［12］FOX J P，GLAS C A W.Bayesian estimation of a multilevel IRT model using Gibbs sampling［J］.Psychometrika，2001，66（2）：271－288.

［13］甘源媛，余嘉元.改进3PL模型参数估计的 MCMC算法［J］.心理科学，2010，33（5）：1212－1215.

［14］涂冬波，漆书青，蔡艳，等.IRT参数模型估计的新方法——MCMC算法［J］.心理科学，2008，31（1）：177－180.

［15］PATZ R J，JUNKER B W.Applications and extensions of MCMC in IRT：multiple item types，missing data，and rated responses［J］.J Educ Behav Stat，1999，24（2）：146－178.