不确定时滞状态饱和系统的稳定性分析与综合
杨 瑾,景 丽
(沈阳师范大学 数学与系统科学学院,沈阳 110034)
饱和系统是在实际工程控制问题中普遍存在的一类非线性控制系统。在大多数的实际控制系统中,无论是执行器或系统状态等工作参数都受到上下界的限制,如机器零件可承受的工作参数,锅炉的炉温,水位的高度等都要受到上下界限的限制,这就是非线性饱和控制系统所研究的问题。对饱和系统的研究包括状态饱和[1-6],执行器饱和[7-11]等。目前,对状态饱和系统的研究都集中在对其稳定性的研究上。
针对不确定系统的稳定性研究引起了众多学者的关注,并取得了一定的研究成果[4-8,12-16]。目前,对于系统的不确定项有两种形式的限定,其一是不确定项为已知系统矩阵的线性组合[4,12],其二是不确定项满足范数有界不确定结构[13-16]。控制系统普遍存在滞后现象,若忽略对滞后现象的考虑,那么系统的稳定性和动态性能将大大改变。滞后现象是影响系统动态性改变的根本原因,可见,对时滞系统进行研究也有其实际的应用价值[7-9,13-16]。因此,针对不确定时滞系统进行研究是十分必要的。
本文采用处理状态饱和函数的凸组合方法及控制系统的Lyapunov稳定性理论,研究不确定时滞状态饱和系统的稳定性问题,给出了系统大范围渐近稳定的充分条件。通过变量变换和矩阵理论,系统稳定的充分条件化为线性矩阵不等式形式,同时给出了系统的状态反馈控制器的设计方法。最后,使用Matlab软件进行仿真,验证了结论的有效性和可行性。
1 问题描述
考虑不确定时滞连续状态饱和系统:
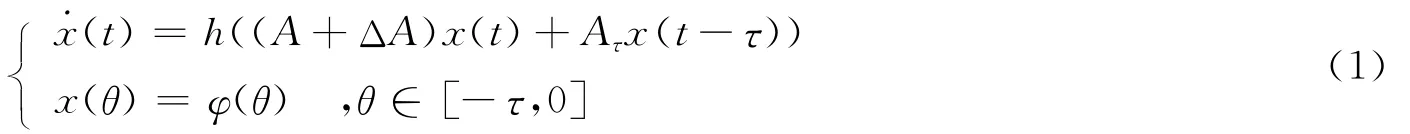
其中:x∈Dn={x|x=(x1,x2,…,xn)∈Rn:-1≤xi≤1,i=1,2,…,n}⊆Rn是状态向量;A=(aij)∈Rn×n是已知的实矩阵;ΔA=HF(t)E=(Δaij(t))∈Rn×n具有范数有界不确定结构,这里,H、E是已知的适维实矩阵,F(t)是Lebesgue可测不确定矩阵,且满足不等式FT(t)F(t)≤I;h(·)为状态饱和函数,具有式(2)的形式:

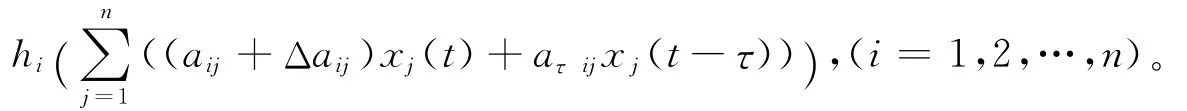
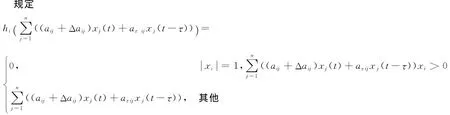
在系统(1)中,状态变量被定义在单位矩形域Dn中,当且仅当状态变量=1,并且满足+Δaij)xj(t)+aτijxj(t-τ))xi>0时,状态饱和限制才发生作用。
引理1 考虑如下的非线性系统

其中,f(0)=0,假设系统(3)的状态轨线都在ℑ内,如果存在函数V(x):ℑ→R,使得φ1(‖x‖)<V(x)<φ2(‖x‖),∀x∈ℑ,并且≤-φ3(‖x‖),∀x∈ℑ,其中φ1,φ2,φ3都是K-函数,则系统(3)在原点大范围渐近稳定。(系统在原点大范围渐近稳定是指系统的吸引域为ℑ)

令Dn是有对角元素是1或0的对角矩阵组合的集合,则Dn包含2n个元素,令Di∈Dn,并定义=I-Di。
引理3[5]设G=(gij)∈Rn×n是对角占优矩阵,且对角元素为负,即gii<0,(i=1,2,…,n),则
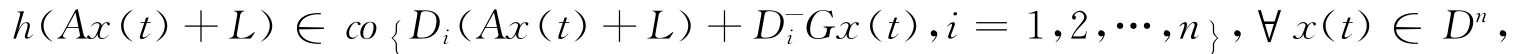
其中L∈Rn。
2 主要结论
定理1 如果存在正定对称矩阵X∈Rn×n、Z∈Rn×n和矩阵Y∈Rn×n以及正实数ε,使得

证明 选取Lyapunov函数
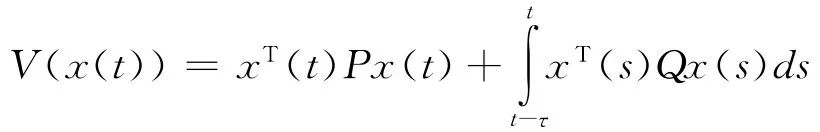
其中P、Q∈Rn×n为正定对称矩阵,于是沿着系统(1)有

设G=(gij)∈Rn×n是对角元素为负的对角占优矩阵,由引理3,可知

其中Di、(i=1,2,…,2n)如引理2所定义的。
令=Di(A+ΔA)+,则

根据引理1可知,若
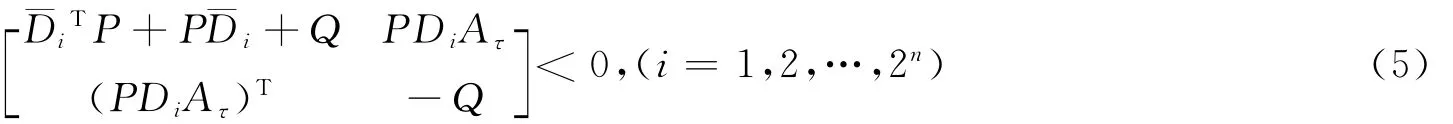
则˙V(x(t))<0,那么系统(1)在原点大范围渐近稳定。
由Schur引理,式(5)等价于
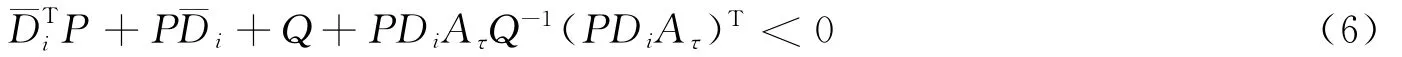
由于,矩阵ΔA具有范数有界不确定结构,式(6)成立等价于

将式(7)左、右分别乘以P-1,即得由Schur引理,式(8)成立等价于


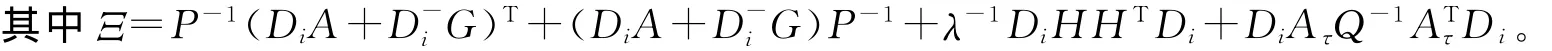
令P-1=X,GP-1=GX=Y,Q-1=Z,λ-1=ε,且G=YX-1是行对角元素为负的对角占优矩阵,式(9)化为式(4),不等式(4)为线性矩阵不等式,即可使用Matlab软件进行求解。
3 系统状态反馈控制器的设计
考虑下面的状态饱和系统的控制器设计问题:

其中:矩阵B=(bij)∈Rn×m;K=(kij)∈Rm×n;其他参数同系统(1)。
定理2 考虑系统(10)在线性状态反馈控制器为u(t)=Kx(t)=WX-1x(t)作用下,如果存在正定对称矩阵X∈Rn×n、Z∈Rn×n和矩阵Y∈Rn×n,W∈Rm×n以及正实数ε,使得

证明 将u(t)=Kx(t)代入到式(10)中,系统(10)改写为
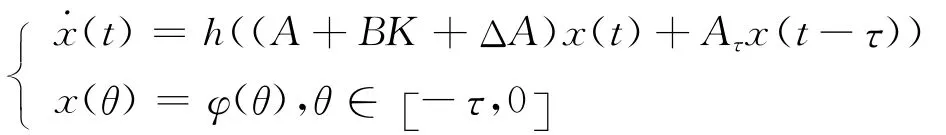
在定理1的证明中将式(9)改写为


将式(13)化为式(11),不等式(11)为线性矩阵不等式,即可通过 Matlab软件进行求解,并且系统(10)渐近稳定的线性状态反馈控制器为u(t)=Kx(t)=WX-1x(t)。
4 仿真算例
设系统(10)中的矩阵参数为
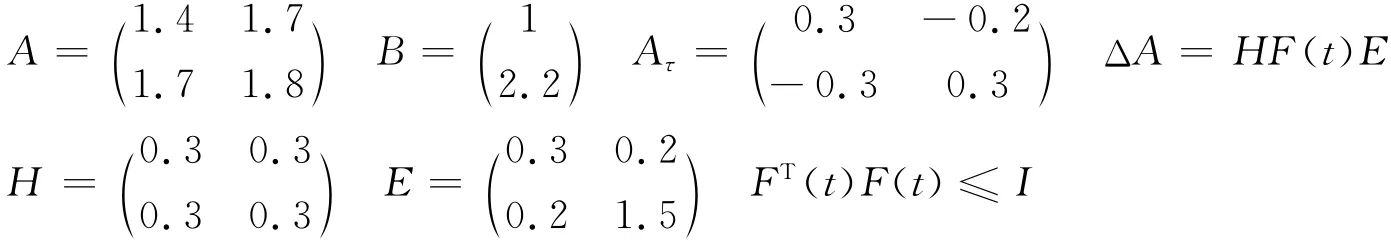
利用MATLAB工具箱中的feasp函数求解不等式(11),得到
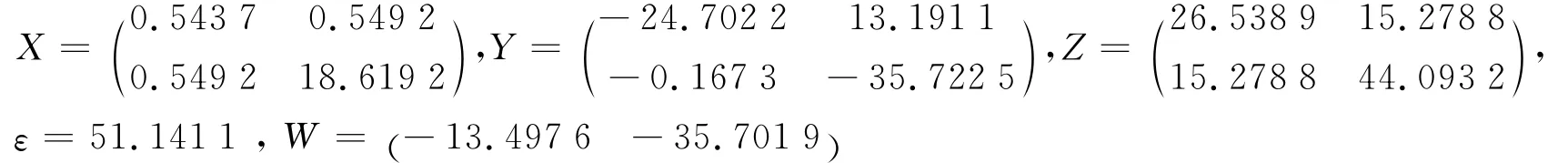
同时得到

由矩阵G是对角元素为负的对角占优矩阵,状态反馈

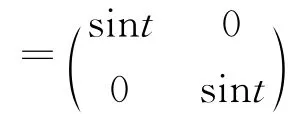
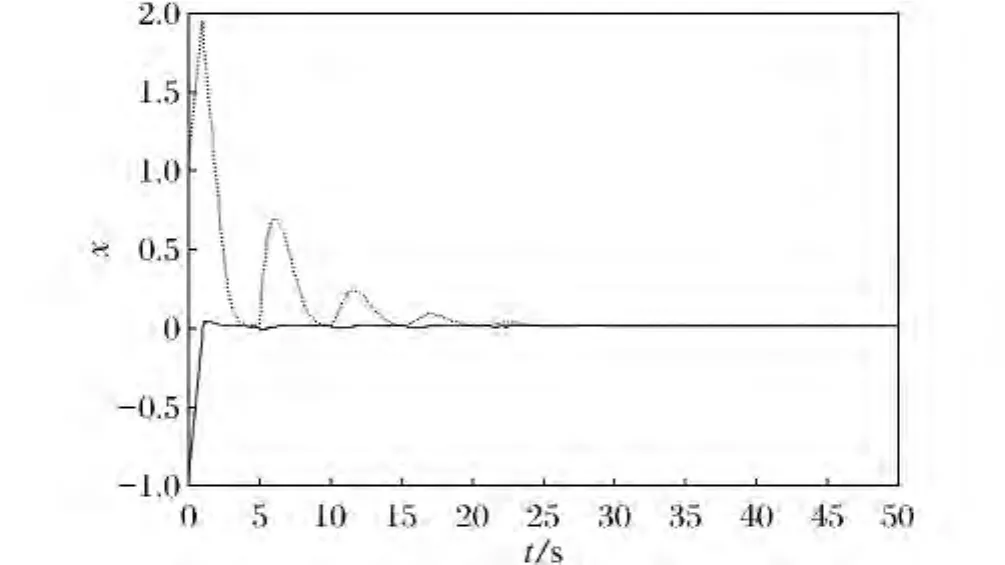
图1 系统(10)状态反馈控制后的状态轨迹
5 结 语
本文研究带有不确定项的时滞状态饱和系统,选择适当的Lyapunov函数,并将非线性状态饱和函数表示成凸组合的形式,给出系统在原点大范围渐近稳定的充分条件,将其表示成线性矩阵不等式(LMI)的形式,同时给出了系统状态反馈控制器的设计方法,通过Matlab软件进行仿真,验证结果的有效性和可行性。
[1]李慧,景丽.离散线性状态饱和控制系统的稳定性[J].沈阳师范大学学报:自然科学版,2012,30(3):331-334.
[2]SINGH V.New approach to stability of 2-D discrete systems with state saturation[J].Signal Proc,2012,92(1):240-247.
[3]SINGH V.Novel criterion for stability of discrete-time systems in a state-space realization utilizing saturation nonlinearities[J].Appl Math Comput,2011,218(8):4305-431.
[4]陈东彦,李兴伟,石宇静.不确定状态饱和线性系统的鲁棒稳定性分析[J].哈尔滨理工大学学报,2013,18(3):77-82.
[5]张象林,陈东彦.连续线性状态饱和系统鲁棒稳定性分析[J].哈尔滨理工大学学报,2012,17(2):31-35.
[6]KANDANVLI V K R, KAR H.Robust stability of discrete-time state-delayed systems with saturation nonlinearities:linear matrix inequality approach[J].Signal Proc,2009,89(2):161-173.
[7]MA Yongmei,YANG Guanghong,GUAN Wei.Robust stabilization of switched discrete-time systems with actuator saturation[J].J Control Theory Appl,2009,7(4):454-458.
[8]ZHANG Minsong.Robust Stabilization for Uncertain Stochastic Multiple Time-Delay Systems with Actuator Saturation:An LMI Approach[J].Procedia Eng,2012,29:935-939.
[9]WANG Mao,GU Yue,LI Xianwei.Further control synthesis for time-delay systems with actuator saturation[J].J Control Theory Appl,2013,11(1):128-131.
[10]CHEN Yonggang,FEI Shumin,ZHANG Kanjian,et al.Control synthesis of discrete-time switched linear systems with input saturation based on minimum dwell time approach[J].Circuits,Syst,Signal Proc,2012,31(2):779-795.
[11]LIU Leipo,SONG Xiaona,FU Zhumu,et al.Local stabilization for unstable bilinear systems with input saturation[J].Nonlinear Dyn,2012,70(1):249-254.
[12]DING Baocang.Robust model predictive control for multiple time delay systems with polytopic uncertainty description[J].Int J Control,2010,83(9):1844-1857.
[13]肖乐,伞冶,朱弈.不确定线性时滞系统时滞相关状态反馈鲁棒镇定[J].系统工程与电子技术,2013,35(4):802-806.
[14]WENG Falu,MAO Weijie.Robust stability and stabilization of uncertain discrete singular time-delay systems based on PNP Lyapunov functional[J].IMA J Math Control Inf,2013,30(3):301-314.
[15]YAN Dongmei,WANG Youwei,WEI Jiuhong,et al.Delay-Dependent Observers for Uncertain Nonlinear Time-Delay Systems[J].TELKOMNIKA Indonesian J Electrical Eng,2013,11(5):2394-2401.
[16]KANDANVLI V K R,KAR H.Delay-dependent Stability Criterion for Discrete-time Uncertain State-delayed Systems Employing Saturation Nonlinearities[J].Arabian J Sci Eng,2013,38(10):2911-2920.

