空旷平坦地面非平稳强风湍流特性研究
张少锋,楼文娟,吕中宾,段志勇,黄铭枫
(1.河南省电力试验研究院,郑州 450002;2.浙江大学土木工程学系,杭州 310058)
空旷平坦地面非平稳强风湍流特性研究
张少锋1,楼文娟2,吕中宾1,段志勇2,黄铭枫2
(1.河南省电力试验研究院,郑州 450002;2.浙江大学土木工程学系,杭州 310058)
根据1128h的实测强风风速样本,对某空旷平坦地貌下10 m高度处的非平稳强风风场湍流特性进行了研究。基于平均风速在基本时距内的平稳性,建立了非平稳强风风场的平稳风速模型和非平稳风速模型,分别计算这两类模型下的各风场湍流特征参数并加以对比。结果表明:55%的实测风速样本具有较强的非平稳性,采用非平稳风速模型更能反映实际风场风速;研究湍流特征参数随平均风速的变化规律,其中湍流强度随风速变化不明显,主要集中在0.16~0.20,大于我国现行荷载规范规定的B类场地10 m高度湍流度值0.14;阵风因子随平均风速减小,湍流积分尺度则随之增大;相对于其他风速谱,Davenport谱更能准确描述强风风场的能量分布。
风速实测;经验模态分解;风速模型;非平稳性;湍流特性
风荷载是结构设计中必须考虑的动力荷载,其动力特性主要是由风场的湍流特征决定的。风场的湍流特性主要包括湍流强度、阵风因子、湍流积分尺度和脉动风速谱等。基于现场实测技术得到风速记录并加以分析,是目前最直接最有效的研究风场湍流特性的手段。近年来,国内已有不少文献[1-5]对建筑结构一定高度处(一般在顶部)风速的湍流特性进行了实测研究,为认识脉动风速湍流特性提供了宝贵资料;然而,我国规范以空旷平坦地貌下10 m高度处的风场为参考标准,而已有的文献对该地貌同高度下的风场湍流特性的研究鲜有涉及。因此,开展10 m高度空旷平坦地貌(标准地貌)的风场湍流特性研究具有重要的现实意义。
在以往的风特性研究中,通常假定风荷载为平稳高斯随机过程;而大量现场实测风速记录[6-8]表明,在复杂场地条件或强风等高湍流风场下,风荷载常常表现为非平稳性,基于风速平稳性假定的计算结果不能如实反映风场的湍流特性。针对这一问题,徐幼麟等[9]引入信号分析理论中的经验模态法(Empirical Mode Decomposition,简称EMD法),提出将非平稳风速分解为时变平均风速和零均值平稳脉动风速,有效地解决了实测风速的非平稳性问题。
本文根据某空旷平坦地貌下10m高度实测得到的1 128 h强风风速样本,采用EMD法建立非平稳风速模型,基于该模型计算各风速下湍流特征参数,包括湍流强度、阵风因子、湍流积分尺度和风速谱等,并与平稳风速模型的对应值进行对比,以研究风场湍流特性的合理表达。
1 非平稳风场风速模型
1.1 平稳风速模型
通常采用矢量分解法对实测风速样本进行分解,得到沿风速主向的纵向风速时程和垂直风速主向的横向风速时程,具体求解过程参见文献[10]。
现有的风场特性分析假定实测风速记录为平稳过程,即基本时距内平均风速为恒定不变值,故实测风速可表示为:

上述过程得到的风速模型称为平稳风速模型。计算该模型的脉动风速自相关函数,并通过快速傅里叶变换(FFT),可以估计风场的功率谱密度。然而,基于平稳过程假定导致平稳风速模型的脉动风速时程具有较强的非平稳性,且矢量分解法将偏离主方向的风速强行分解到该风向的垂向和平行向,加剧了该模型的脉动风速非平稳性。由于FFT只对平稳信号具有较好的处理能力,直接对该模型的脉动风速进行计算,将产生较大的误差。
1.2 非平稳风速模型
大量强风实测记录表明,复杂地形等高湍流风场的风速平均值并非恒定的,而是随时间在不断变化,通过EMD法可以提取该平均风速变化历程。
EMD法是由美国NASA的黄锷[11]提出的一种信号处理方法,它在处理非平稳和非线性数据上具有优于其它方法的明显优势。EMD法假定,任何信号都是由固有振动模式构成,且信号是一簇固有模式函数(Intrinsic Mode Function,即IMF)的和。最先分解得到的IMF为信号中频率最高的成分,随着IMF阶数的增加,其频率逐渐降低,最后得到频率成分最低的信号,称为趋势项。对于风速信号而言,各阶IMF对应不同频率的脉动风速,趋势项则对应频率最低风速分量,即平均风。EMD法通过一个筛选(shifting process)的分解过程得到各阶IMF和趋势项。具体筛选过程参见文献[12]。
一般认为实测风速记录中风速周期远大于结构固有周期的成分可视为平均风分量,EMD法则将单调的趋势项作为平均风成分处理,采用这种筛选标准需要循环多次,比较耗机时。事实上,对各阶IMF的功率谱分析表明,低频段的IMF频率已经足够低,可将这部分IMF视为平均风成分。因此,一般将原信号筛选几次后,即可获得风速的平均风成分[13]。
由EMD法筛选得到的趋势项是随时间不断变化的,即平均风分量是时间的函数。因此,实测风速可表示为:

上述风速模型即为非平稳风速模型。由于平均风速随时间变化,故称之为时变平均风速;脉动风速可认为是统计参量随时间不变的零均值平稳过程。
2 风速模型平稳性检验
为研究我国规范规定的标准地貌(空旷平坦地貌)在标准参考高度(离地面10 m)处的风场特性,设立了测风塔并采用三维风速仪进行连续观测。
实测风场位于河南省开封市,场地周边平坦,四周为农田,按照《建筑结构荷载规范》有关地表粗糙度的分类标准,该场地为典型的B类风场。对2013年2月1日~3月19日期间,总计观测时间为1 128 h的风速进行了连续记录。将实测风速样本分割为1 128个子样本,每个子样本的记录时长约为1 h;对记录过程中数据缺失时段不予插值处理。图1(a)为某实测子样本的风速时程。
采用矢量分解法计算每个子样本的纵、横风向风速时程,并应用轮次检验法对各风速时程进行处理,以检验信号的平稳性。处理前对数据缺失较多或风速失真严重的子样本予以剔除,得到970个有效序列。平稳性检验结果显示,当显著性水平为0.05时,仅436个子样本的顺风向风速时程具有平稳性,占总数的45%;而横风向风速时程样本中满足平稳性假定的子样本数为924个,占总数的95%左右。这说明,与台风等强风气候类似,本文研究的大部分实测风速子样本的顺风向时程具有非平稳性,风速平稳性假设与实际情形不符;而横风向风速时程则较好地符合了平稳性假定,可视其为一平稳的随机过程。下文主要研究实测风速的顺风向湍流特征参数。
从实测风速记录中选出平均风速较大的52组风速子样本,选取原则为:1 h风速记录较完整且平均风速大于6 m/s。建立每个子样本的平稳风速模型和非平稳风速模型,分别得到两类模型的平均风速和脉动风速,如图1(b)~(d)所示。从图中可以看出,相比于平稳风速模型,非平稳风速模型的时变平均风速更好地反映了风速的变化趋势;该模型的脉动风速明显更具有平稳性,基本为零均值平稳过程。
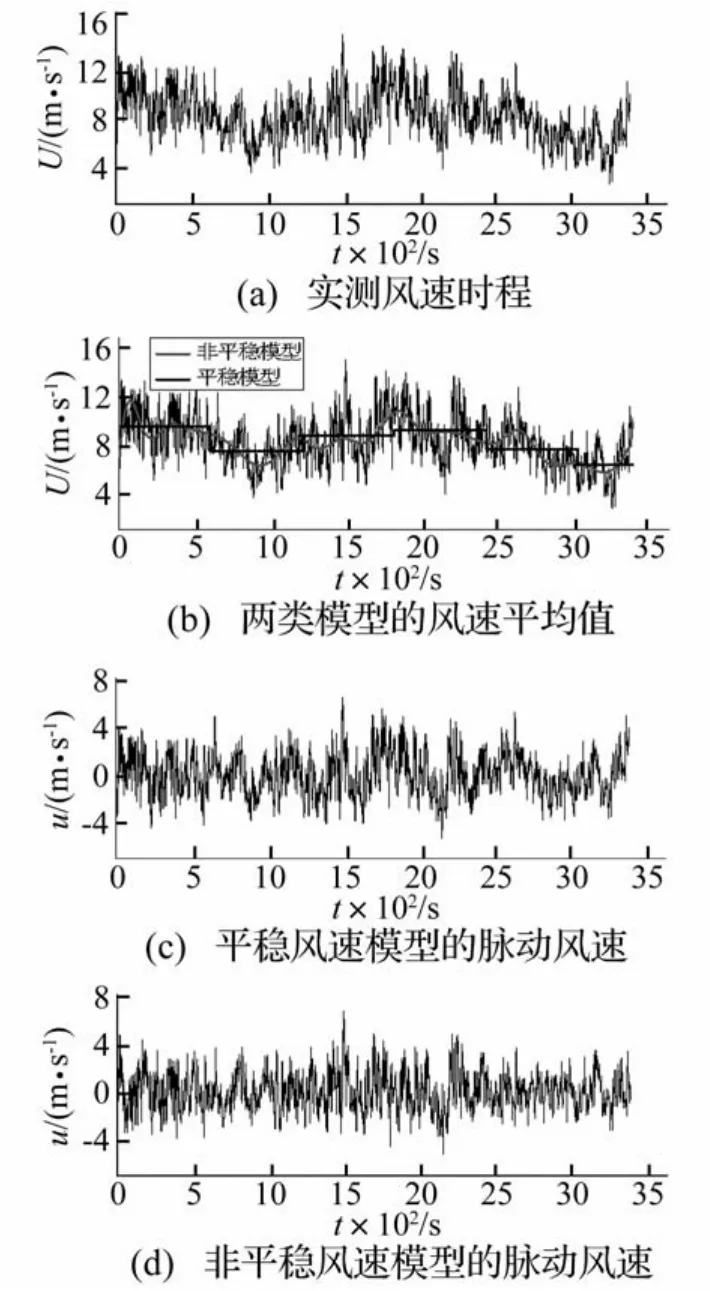
图1 某实测1h风速时程Fig.1 Time history of wind velocity in an hour
3 风场湍流特性分析
3.1 概率密度函数
研究风速的概率密度分布可以检验信号是否具有高斯性,并为设计风荷载的确定提供依据。通常认为,脉动风的概率分布呈0均值的标准正态分布,其概率密度函数表达式为:

式中,σu为风速的标准差,f(u)为风速概率密度。计算实测风速的偏度系数和峰度系数可以检验风速数据的高斯分布特性。若风速分布符合高斯假定,则偏度系数为0,峰度系数为3。
针对52组有效样本的脉动风速时程,计算两类风速模型的概率密度分布,并与标准正态函数进行对比。某样本的计算结果如图2所示。从图中可以看出,平稳风速模型的概率密度曲线宽而缓和,与实测风速分布偏离较大;非平稳风速模型的概率密度曲线窄而陡峭,且与实测结果吻合得很好。平稳风速模型的52组样本的平均偏度系数和平均峰度系数分别为0.28和6.23;非平稳风速模型的两个系数对应为0.21和2.96。这说明,采用非平稳风速模型描述的风场风速更符合高斯假定。

图2 某子样本概率密度函数比较Fig.2 Comparison of probability density function
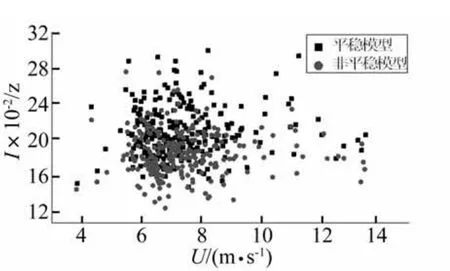
图3 湍流强度对比Fig.3 the comparison of turbulence intensity
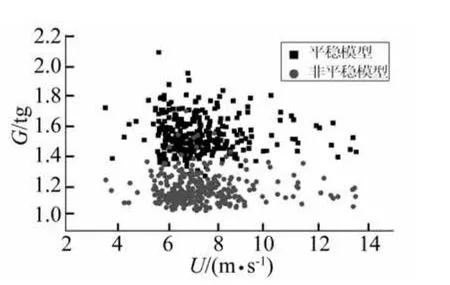
图4 阵风因子与平均风速的关系Fig.4 Relation between gust factors and wind speed
3.2 湍流强度
湍流强度用于描述风场的脉动强度,是计算结构脉动风荷载不可缺少的参数,通常将其定义为基本时距内的脉动风速标准差与平均风速的比值[14],即

式中,I(z)为高度z处的湍流强度;σ(z)、U(z)分别为同一高度处的风速均方根和平均值;基本时距取为T=10 min。
对前述52组风速子样本,计算两类模型下的湍流强度,计算结果如图3所示。从图中可以看出,非平稳风速模型的湍流强度比平稳风速模型的计算值略小,前者主要分布在0.16~0.20之间,后者大部分在0.18~0.22间;湍流强度在各平均风速段的变化不明显。
3.3 阵风因子
阵风因子也可用来表征风场的脉动强度。结构风工程中定义阵风因子为阵风持续期tg内风速平均值与基本时距的风速平均值之比,即[13]:

在计算阵风因子时,通常取tg=3 s。对前述52组风速子样本,计算两类模型下的阵风因子,计算结果如图4所示。
从图中可以看出,非平稳风速模型计算得到的阵风因子明显比平稳风速模型的计算结果小;由非平稳风速模型计算得到的阵风因子为1.17,而由平稳风速模型计算得到的结果为1.54,两者差异显著。对图4各平均风速段的平均阵风因子计算表明,阵风因子随平均风速增大而略有减小。
3.4 纵向湍流积分尺度
湍流积分尺度是气流中湍流涡旋平均尺度的量度[14]。积分尺度的大小决定了脉动风的影响范围。当湍流积分尺度大于空间两点的间距时,涡旋将影响这两个点所在的整个区域,使两点间的脉动风速产生相干性。计算湍流积分尺度的方法很多,研究发现,自相关函数直接积分法是计算大气边界层湍流积分尺度较为准确稳定的方法;而当实测风速谱与Von Karman谱符合得较好时,采用Karman谱反推得到的湍流积分尺度也是较合理的[15]。因此,本文在纵向计算湍流积分尺度时,采用上述两种方法同时计算,以确保结果准确可靠。自相关函数直接积分法计算纵向湍流积分尺度的表达式为:

符合Karman谱的风场其湍流积分尺度可根据自功率谱密度函数直接计算得到[11]:

式中,Su(0)为f=0处的顺风向风速自功率谱密度,σu为脉动风速标准差。
针对前述52组风速子样本,分别采用自相关函数直接积分法和Karman谱反推法计算两类模型下的湍流积分尺度,计算结果如图5所示。

图5 风场纵向湍流积分尺度Fig.5 Along wind turbulence integral scale
从图5可以看出,由自相关函数直接积分法计算得到的湍流积分尺度大部分集中在50 m~200 m,而由Karman谱反推法计算得到的湍流积分尺度较小,其结果大部分集中在0~100 m;这可能是因为自相关函数直接积分法在计算中引入了Taylor假设,使两者结果有差异。
采用自相关函数直接积分法计算时,平稳风速模型和非平稳风速模型计算得到的湍流积分尺度统计值分别为172 m、139 m,采用Karman反推法的计算值分别为117 m、90 m。两种方法计算的湍流积分尺度值均表明,非平稳风速模型的结果比平稳风速模型小,且分布更加集中。
图5还表明,风场的纵向湍流积分尺度随平均风速而增大,由自相关函数直接积分法得到的湍流积分尺度随平均风速变化较缓慢;而由Karman谱反推法计算的结果则随平均风速增大而显著变大。说明当风场移动速度增大时,风场漩涡对行径范围的影响将扩大。为考察纵向湍流积分尺度随高度的变化关系,对国内学者的研究成果进行归纳,结果列于表1。从表1可以看出,随着竖向高度的增加,纵向湍流尺度逐渐增大;当竖向高度大于梯度风高度后,该值减小。

表1 纵向湍流尺度随高度的变化关系Tab.1 Variation of along wind integral scale for height
3.5 风速功率谱密度
脉动风速功率谱反映风场能量在频域的分布情况,是描述风场脉动特性的重要指标。按照风速风向关系,有纵向、横向和竖向风速功率谱密度。常用的纵向风速功率谱有Davenport谱、Von Karman谱和Kaimal谱等,形式如式(8)。

式中,Su(f)为纵向风速功率谱密度,x=1 200f/v10,y=/v10,f为频率,v10为10 m高风速,Lu为湍流积分尺度,取上文由Karman谱反推法计算得到的结果。k为地面粗糙度系数,根据实测数据按k=计算得到。
研究表明,结构主要对处于低频段的风荷载作用较敏感,一般认为这一范围为0.001~0.4 Hz;本次风场实测中,风速的采集频率为1 Hz,根据采样定理可知,实测数据能够较精确地反映0.5 Hz以下的实际风场能量。另外,由于风暴持续时间一般为1 h左右,因此本文在计算风速谱时,时距选为T=1 h。
对实测的970个有效风速子样本,分别计算两类模型的风速自功率谱密度,并与Davenport谱、Kaimal谱和Von Karman谱三条经验谱曲线进行对比。以莫宁坐标(fz/u)为横坐标,归一化自谱(fSu/σ2u)为纵坐标,取双对数坐标,绘制自功率谱密度曲线,如图6所示。

图6 纵向风速自功率谱Fig.6 the longitudinal fluctuation wind speed spectra
从图6可以看出,对于两类风速模型,在峰值频率右端,Davenport谱和Von Karman谱均能较好地描述风场能量随频率的分布关系,Kaimal谱则有所高估;而在峰值频率左端,Von Karman谱和Kaimal谱的功率谱估计均偏大,Davenport谱与实测曲线最接近。因此,Davenport谱能最准确地描述风场的能量分布。
为定量评估两类模型下,各平均风速段的自谱与经验谱的偏差,采用式(9)的计算指标进行衡量[16]:

由式(9)计算得到的两类模型下各风速段的实测纵向风速功率谱与Davenport经验谱的偏差列于表2。从表中可以看出,高风速下Davenport谱与实测谱偏差较小,Davenport谱能够较精确地描述强风的风场能量分布。

表2 实测谱与Davenport谱偏差与平均风速关系Fig 2 Variation of deviation between measured and Davenport spectra for wind speed
4 结 论
本文根据某空旷平坦地貌下10 m高度处实测得到的1 128 h非平稳强风风速样本,建立平稳风速模型和非平稳风速模型,并计算两类模型下的各风场湍流特征参数,得到以下结论:
(1)实测风速样本具有较强的非平稳性,非平稳风速模型考虑了平均风速的时变性,能更好地反映实际风场风速;
(2)通过计算各湍流特征参数随平均风速的变化规律,表明,湍流强度随风速变化不明显,主要集中在0.16~0.20之间,规范规定同类场地下10 m高度处的湍流强度为0.14,比实测湍流强度略小;阵风因子随平均风速减小,湍流积分尺度则随之增大;
(3)将Davenport谱、Von Karman谱和Kaimal谱三条经验谱曲线与实测谱进行对比,结果表明,Davenport谱能最准确地描述风场的能量分布,尤其在高风速段,低风速段该谱的精度降低。
(4)值得注意的是,本文实测得到的风速样本中,平均风速达到10 m/s(工程中规定强风风速范围为10.8 m/s~13.8 m/s)的子样本数较少,强风样本容量略有不足。进一步研究中,需对更多强风样本进行检验。
[1]郅伦海,李秋胜,胡非.城市地区近地强风特性实测研究[J].湖南大学学报(自然科学版),2009,36(2):8-12.
ZHI Lun-hai,LI Qiu-sheng,HU Fei.Field measurements of strong wind characteristics near ground in urban area[J].Journal of Hunan University:Natural Science,2009,36(2):8-12.
[2]刘浩.北京城区近地面强风场的统计特性[D].北京:北京交通大学,2010:14-69.
[3]顾明,匡军,韦晓,等.上海环球金融中心大楼顶部良态风风速实测[J].同济大学学报:自然科学版,2011,39 (11):1592-1592.
GUMing,KUANGJun,WEIXiao,etal.Field measurements of strong wind speed of normal climate on top of Shanghai World Financial Center[J].Journal of Tongji University:Natural Science,2011,39(11):1592-1592.
[4]顾明,匡军,全涌,等.上海环球金融中心大楼顶部风速实测数据分析[J].振动与冲击,2009,28(12):114-118.
GU Ming,KUANG Jun,QUAN Yong,et al.Analysis of measured wind speed data on top of SWFC[J].Journal of Vibration and Shock,2009,28(12):114-118.
[5]罗尧治,蔡明程,孙斌,等.国家体育场大跨度屋盖结构风场实测研究[J].振动与冲击,2012,31(3):64-68.
LUO Yao-zhi,CAI Ming-cheng,SUN Bin,et al.Field measurement of wind characteristics on roof of the national stadium[J].Journal of Vibration and Shock,2012,31(3):64-68.
[6]Li Q S,Fang J Q,Jeary A P,et al,Full scale measurements of wind effects on tall buildings[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,74(1):741 -750.
[7]Li Q S,Xiao Y Q,Wong C K,et al.Field measurements of typhoon effects on a super tall building[J].Engineering Structures,2004,26(2):233-244.
[8]Fang J Q,Li Q S,Liu D K,et al.Wind effects on a very tall building and wavelet analysis[J].Proceedings of the ICEStructures and Buildings,2000,140(2):151-159.
[9]Xu Y L,Asce M,Chen J.Characterizing nonstationary wind speed using empirical mode decomposition[J].Journal of Structural Engineering,2004,130:912-920.
[10]阎启,谢强,李杰.风场长期观测与数据分析[J].建筑科学与工程学报,2009,26(1):37-42.
YAN Qi,XIE Qiang,LI Jie.Long-term observation and data analysis of wind field[J].Journal of Architecture and Civil Engineering,2009,26(1):37-42.
[11]Huang N E,Zheng S,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London.Series A:Mathematical,Physical and Engineering Sciences,1998,454(1971):903-995.
[12]陈隽,徐幼麟.经验模分解在信号趋势项提取中的应用[J].振动、测试与诊断,2005,25(2):101-104.
CHEN Jun,XU You-Lin.Application of EMD to signal trend extraction[J].JournalofVibration,Measurement&Diagnosis,2005,25(2):101-104.
[13]吴本刚.高层建筑实测风环境和风致响应的非平稳性分析研究[D].广州:广州大学,2012:32-36.
[14]希缪,斯坎伦.风对结构的作用:风工程导论[M].第2版.刘尚培,项海帆,谢霁明,译.上海:同济大学出版社,1992:33-45.
[15]庞加斌,葛耀君,陆烨.大气边界层湍流积分尺度的分析方法[J].同济大学学报,2002,30(5):622-626.
PANG Jia-bin,GE Yao-jun,LU Ye.Methods for analysis of turbulence integral length in atmospheric boundary layer[J].Journal of Tongji University,2002,30(5):622-626.
[16]肖仪清,孙建超,李秋胜.台风湍流积分尺度与脉动风速谱[J].自然灾害学报,2006,15(5):45-53.
XIAO Yi-qing,SUN Jian-chao,LI Qiu-sheng.Turbulence integral scaleandfluctuationwindspeedspectrumof typhoon:an analysis based on field measurements[J].Journal of Natural Disasters,2006,15(5):45-53.
Nonstationary strong wind characteristics over an open flat terrain
ZHANG Shao-feng1,LOU Wen-juan2,LÜ Zhong-bin1,DUAN Zhi-yong2,HUANG Ming-feng2
(1.Henan Electric Power Testing and Research Institute,Zhengzhou 450052,China;2.Department of Civil Engineering,Zhejiang University,Hangzhou 310058,China)
The turbulent characteristics of nonstationary strong wind were analyzed based on field measured wind records of 1128-h long collected at a height of 10 meters over an open flat terrain.According to the assumption that the average wind speed component was deterministic time-varying in a time interval,a nonstationary wind model was proposed and then applied to find its turbulent characteristics.The results were compared with those calculated with a stationary wind model where the average wind speed component was assumed constant.It was found that 55%samples of wind records are nonstationary,and the nonstationary wind model is more appropriate for charactering wind speed.The variations of turbulent characteristics versus wind speed were studied,and it showed that the turbulent intensity seems to have no significant relationship with wind speed and mainly distributes within 0.16~0.20,it is slightly greater than 0.14 given in our current country's wind load codes;the gust factor decreases with increase in the average wind speed,the turbulent integral scale increases with increase in the average wind speed;Davenport spectrum tends to be more accurate to characterize the energy distribution than other wind spectra.
field measurements;empirical modede composition;wind speed model;non-stationarity;turbulent characteristics
TU391
A
10.13465/j.cnki.jvs.2014.23.013
国家电网公司科技项目;国家自然科学基金面上项目(51178424)
2013-09-03 修改稿收到日期:2013-09-30
张少锋男,工程师,1977年生
楼文娟女,博士,教授,1963年10月生

