车辆传动系统非线性平移扭转耦合振动响应灵敏度研究

黄 毅，刘 辉，2，项昌乐，2，杨志刚

（1．北京理工大学机械与车辆学院，北京 100081；2．特种车辆研究所，北京 100081）

车辆传动系统非线性平移扭转耦合振动响应灵敏度研究

黄 毅1，刘 辉1，2，项昌乐1，2，杨志刚1

（1．北京理工大学机械与车辆学院，北京 100081；2．特种车辆研究所，北京 100081）

随着对齿轮传动系统动态品质要求的提高，仅固有特性及其灵敏度的分析已经无法满足车辆传动系统动态特性分析的要求，对强迫振动下响应特性的灵敏度研究可为减振设计提供进一步的指导。研究非线性动力学响应对轴段扭转刚度、质量点惯量以及轮齿啮合误差的灵敏度。将某车辆传动系统样机作为研究对象，以发动机激励作为输入，建立平移扭转耦合集中参数动力学模型。模型中考虑时变啮合刚度、齿侧间隙、轮齿制造、安装误差以及质量偏心等非线性因素，通过直接求导法建立灵敏度方程，利用数值求解的方法获得动力学响应对设计参数的相对灵敏度并进一步将其转化成工程中有实际意义的物理量的灵敏度结果，为齿轮传动系统基于动态响应的参数修改、模型修正和参数优化等方面提供理论依据。

车辆传动系统；集中参数法；平移扭转耦合；非线性；响应灵敏度

机械结构的振动问题主要包括固有频率问题、振型问题和动力响应振幅问题。相应的动力学特性对设计参数的灵敏度分析也在以上几个情况下进行。

在齿轮系统固有特性灵敏度分析中，Chen等［1］采用线性模型在纯扭转振动模式和平移扭转耦合振动模式下研究定轴齿轮固有频率对啮合刚度的灵敏度。Botman等［2－3］以单级行星排作为研究对象，用数值方法分析了固有频率对行星和齿圈支承刚度的灵敏度；Lin等［4－5］则对单级行星排采用两自由度模型用解析法研究其固有特性对设计参数的灵敏度。Guo等［6］以复合行星排为对象，将固有特性灵敏度的分析提升到系统级别，对调谐和失谐系统中固有特性对设计参数的灵敏度进行研究。

而齿轮系统动力学响应灵敏度的分析分别在线性和非线性的理论基础上展开。以线性理论为基础的响应灵敏度分析中，张义民等［7］针对直接法和摄动法进行灵敏度分析产生长期项的问题，通过对灵敏度方程的解耦并结合傅里叶级数有效消除了长期项，给出了消除长期项判断法则。在车辆传动系统中，刘辉等［8］建立线性纯扭转集中质量模型，用直接求导法推导了齿轮传动系统扭振角位移和轴段附加扭振应力对轴系刚度的灵敏度计算公式。黄毅等［9］在进行线性系统响应灵敏度分析时考虑平移与扭转方向坐标的耦合，并将灵敏度同振动能量联系起来。指出了灵敏度分析在平移耦合系统和纯扭转系统中的不同。

除了线性建模之外，齿轮系统中还包含作为参数激励的时变啮合刚度、轮齿在制造和安装过程中的位置偏离理想位置造成的周期性的位移激励、齿侧由于间隙的存在其啮合线变形量和啮合力为分段线性关系所表现出来的强非线性以及齿轮系统中各部件旋转中心和质量中心不重合造成的质量偏心等非线性因素。而目前对车辆传动系统响应灵敏度分析中，大多并未考虑上述各种非线性因素的影响。Zhao等［10］在蜗杆蜗轮啮合的研究中加入了中心距误差、轴角误差以及蜗杆蜗轮轴向位置误差的影响，用数值方法获得蜗杆蜗轮啮合力对以上因素的灵敏度。Athervale等［11］研究了系统振动对制造和装配过程中的误差的灵敏度。Petrov［12］在研究汽轮机叶片动力学特性时考虑了不同间隙的影响，推导了响应频率和共振情况下的响应级对间隙的灵敏度。但以上并未对系统动力学响应对各种非线性因素进行详细的灵敏度分析。故对车辆传动系统进行包含多种非线性因素的响应灵敏度分析变得非常必要。

本文以某车辆传动系统样机作为研究对象，采用发动机激励输入，建立了平移扭转耦合集中参数动力学模型。模型中考虑啮合刚度的时变性、齿侧间隙、轮齿在制造和安装等过程中的误差以及质量偏心等非线性因素的影响，通过理论推导和数值求解获得了动态响应对设计参数的灵敏度，并进一步推导出有实际工程意义的物理量对扭转刚度、惯量以及轮齿误差的相对灵敏度结果，为动力学修改和动态优化等提供理论基础。

1 响应灵敏度方程的建立

前面提到文献［9］中建立线性平移扭转耦合系统基于响应的灵敏度方程组。本文在此基础上引入时变啮合刚度、各点的质量偏心、轮齿啮合的综合传动误差和齿侧间隙等非线性因素采用文献［9］中的方法建立非线性系统基于响应的灵敏度方程组（1）。

式（1）中x，y平动位移坐标，θ为扭转位移坐标；j为质量点编号；c表示设计参数；Fa／Ta表示惯性力／力矩；Fb表示同一轴上各质量点之间的相互作用力；Fe／Te表示质量偏心力／力矩；Tt表示两质量点之间的扭转力矩；Fn／Tn表示非轴上接触力／力矩；∂Fb／∂c和∂Tt／∂c的表达式见文献［9］，其它各量表达式如下面式（2）～式（6）所示。

式（2）中Fe／Te如式（2）以及Ta如式（3）中考虑了质量偏心的影响，m为质量，e为质量偏心距，ψ为质量偏心角，ω表示转速。

不同部件承受的非轴上接触力／力矩Fn和Tn对设计参数c的灵敏度∂Fn／∂c和∂Tn／∂c具有不同表达式，接下来以质量点j为对象分别进行说明。

（1）离合器

离合器有接合和断开两种状态，断开时对设计参数c的灵敏度表达式为式（4）上式，结合时为下式。其中i（i≠j）表示与离合器接合的质量点编号。

（2）轴承

轴承支反力／力矩Fn／Tn对设计参数c的灵敏度表达式如式（5）。

（3）齿轮

齿轮承受非轴上接触力为轮齿的啮合力，第k对齿轮啮合主被动齿轮之间的啮合线方向的时变啮合刚度kmk（t）随时间变化取矩形波，时变阻尼cmk（t）与啮合刚度相关按公式（7）进行计算，考虑到传动误差ek（t）以及齿侧间隙f（Δk）的作用。其啮合力对设计参数a的灵敏度表达式如式（6）。

式中αk为主被动轮的位置角，βk为压力角，R为基圆半径，mp和mg为主被动齿轮的等效质量，ξ为齿轮啮合的阻尼比。

采用多项式拟合的方式对分段间隙函数f（Δk）以及f（）进行拟合，拟合式以及由其推导的灵敏度公式如式（8）和式（9）。其中h＝1，3，5，…，n，由于h随着次数的增大精度提高有限并耗费机时，当h＝3时就能对分段曲线做很好的近似，拟合曲线的系数取值为：α1＝1．945×10－2，α3＝1．222×107。间隙函数采用分段线性函数时的曲线和多项式拟合时的曲线如图1。

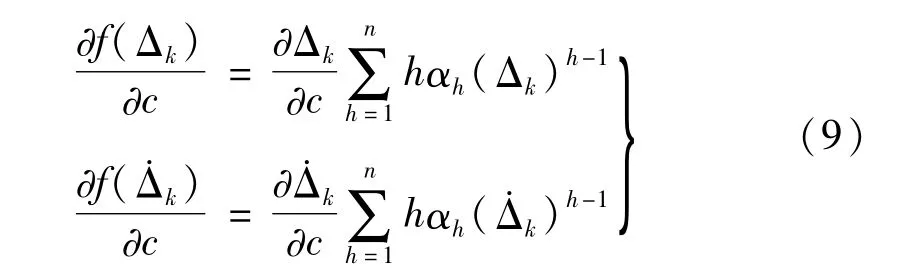
式（9）中啮合线变化量及其对时间导数Δk和对设计参数c的灵敏度表达式如式（10）。

图1 间隙分段函数曲线与拟合曲线Fig．1 The comparison between piecewise curve and fitting curve of backlash function of spur gear pair

k对时间导数，表达式如式（11）；ekpE和ekpA分别为第k对啮合齿轮副主动轮的制造和安装误差幅值，ωkp为其转频；ekgE和ekgA分别为第k对啮合齿轮副被动轮的制造和安装误差幅值，ωkg为其转频；ekpg为第k对啮合齿轮副主被动齿轮误差干涉的的幅值，ωk为其啮合频率。

在进行灵敏度分析时，通常选取便于修改的变量进行计算。本文以系统中质量点j的动力学响应为对象研究其对质量点l的参数的灵敏度。质量点l的参数选取单对齿轮副动力学分析中的支承刚度kl、惯量Jl和传动误差el以及系统级别中的扭转刚度ktl－1，l进行响应灵敏度分析。

（1）动力学响应对轴段扭转刚度灵敏度

此种情况的讨论见文献［9］。

（2）动力学响应对各点转动惯量灵敏度

当c＝Jl（l≠j）时灵敏度表达式如式（2）～式（10）所示；当c＝Jl（l＝j）时，以上其它式不变，式（3）变为式（2）。

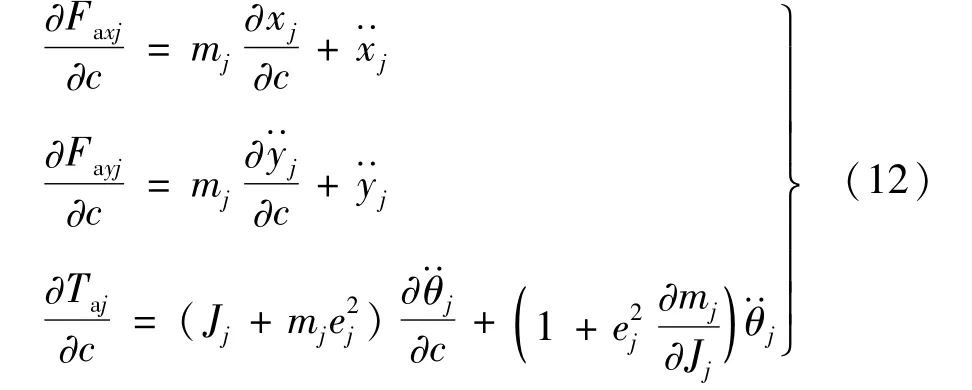
（3）动力学响应对传动误差幅值灵敏度

计算动力学响应对传动误差幅值的灵敏度时表达式如式（2）～式（10）所示。c＝elpE当l≠j的情况如式（13）上式所示；当l＝j的情况如下式所示。

对于计算出的灵敏度结果，利用式（14）可以计算出相对灵敏度。其中φ和为质量点j在i（i＝x，y或ij

θ）方向上动力学响应动力学响应。

其数值仿真流程图如图2所示，其中动力学方程和灵敏度方程均采用定步长的四阶龙格库塔进行计算。

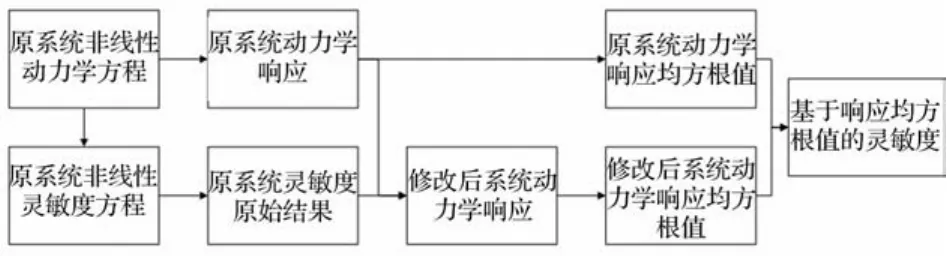
图2 灵敏度结果计算流程图Fig．2 The procedure flow chart of calculating sensitivity

2 系统参数

利用上述方法对某车辆传动系统样机模型进行响应灵敏度分析。该样机能实现8个前进挡位和4个倒挡，CH、BL、BR、C1、C2、C3、C4为换挡离合器，本文进行计算的工况为离合器BL和C4接合，其它离合器分离。另外系统还包括一个输入惯量盘、两个输出惯量盘、11个轴承、7个离合器、4对定轴齿轮副和两个简单行星排共计42个质量点，每个质量点包括x，y和θ三个方向自由度共计126自由度。其动力学模型图如图3所示，图4为行星部分的运动简图。

图3 某样机平移－扭转耦合动力学模型Fig．3 Dynamic model of lateral－torsional coupling system

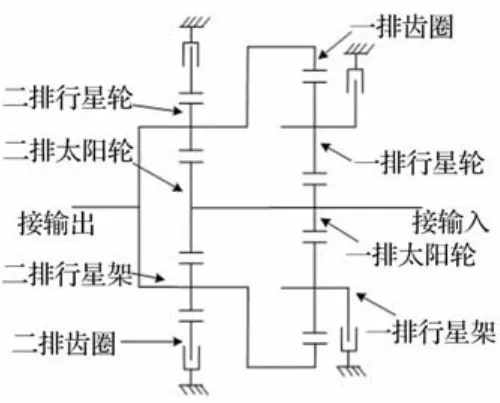
图4 行星部分运动简图Fig．4 Kinematic sketch of planetary gear

图3所示的传动系统采用发动机从质量点1处输入，输入转矩如图5所示。在质量点32和42之间加入等值负载，其和等于输入转矩乘以该工况传动比。将分别计算8种转速下的计算结果，输入转速从2800 r／min－4 200 r／min每200 r／min计算一组值。其中各轴段扭转刚度和各质量点的惯量如表1和表2所示。

图5 发动机输入转矩Fig．5 The input torque of engine

表1 轴段扭转刚度列表Tab.1 Torsional shaft stiffness of the example system shown in Fig.2

表2 惯量列表Tab.2 Moment of inertia of the example system shown in Fig.2

3 数值仿真结果与分析

由于系统中各参数值大小各异，对不同大小的参数研究相同大小的数值摄动情况下灵敏度并无太大实际意义。在工程中往往更关心响应变化量占响应的百分比随参数摄动百分比的变化情况，这就是相对灵敏度。接下来将采用式（14）定义的相对灵敏度公式进行响应灵敏度分析。

3.1 轴段附加扭转力矩对各轴段扭转刚度相对灵敏度

扭转振动系统中振动能量在动能和弹性势能之间转化。各轴段的扭转刚度为弹性储能元件，研究动力学响应对其灵敏度有着重要的意义。图6给出了从2 800 r／min到4 200 r／min共8种输入转速下系统中四段轴的附加扭转力矩对各扭转刚度的相对灵敏度结果。其中附加扭转力矩的定义详见文献［9］。

图6 各转速下轴段附加扭转力矩对各扭转刚度相对灵敏度Fig．6 The relative sensitivity of additional torque of shaft segments with respect to shaft torsional stiffness in different speed

从图6中可以看出轴段对各参数相对灵敏度结果随转速的变化而发生变化，并不是一个定值。对（b）图中轴段21－22和（c）图中轴段25－26而言，不同转速下的各相对灵敏度数值在一定范围内变化，并没有数量级差异的情况出现。而对于（a）图中轴段1－2和（d）图中的轴段32－33，都出现对自身以及邻近扭转刚度的相对灵敏度数值明显区别于其它值的情况。而轴段1－2和32－33分别为系统输入输出端，41－42同为双输出端之一但却没有出现对自身扭转刚度的相对灵敏度较大的情况。从表1中可以看出轴段1－2 和32－33对应的扭转刚度kt1－2和kt32－33数值较小而kt41－42数值较大，这说明在输入输出端附近较小的扭转刚度是造成本身附加扭转力矩对其相对灵敏度较大的原因。结合靠近该两轴段的其它轴段的相对灵敏度结果发现kt1－2和kt32－33对邻近几个轴段附加扭转力矩的影响都较大，特别是在三轴上各轴段的附加扭转力矩对kt32－33和kt33－35的相对灵敏度都较大。

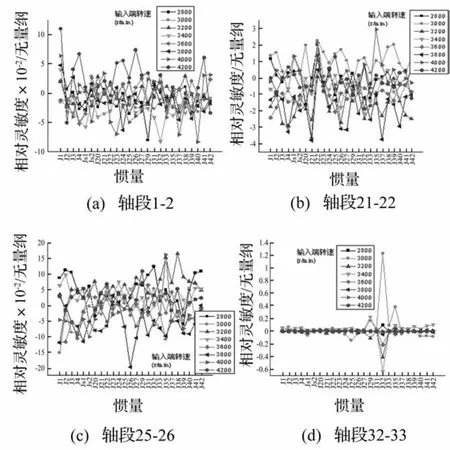
图7 各转速下轴段附加扭转力矩对各点惯量相对灵敏度Fig．7 The relative sensitivity of additional torque of shaft segments with respect to inertia of mass points in different speed

而不同轴段的相对灵敏度数值进行比较时，从图6各图可以看出轴段21－22的相对灵敏度数值比其它轴段大。虽然其它参数的变化造成轴段21－22附加扭转力矩以及振动能量变化数值较小，但由于该轴段不在动力的传动路线上其本身振动能量较小，变化部分占原值百分比较大，于是造成了该轴段附加扭转力矩对各扭转刚度相对灵敏度较大。

结合上面的分析可以知道，非线性系统中响应灵敏度数值随着转速的变化而变化。由于系统是一个整体，系统中任何一个扭转刚度发生变化时各轴段的附加扭转力矩也随之发生变化，在部分轴段中对各扭转刚度的相对灵敏度在一个数量级上并没有出现比其它相对灵敏度大很多的灵敏度。输入输出端附近有较小扭转刚度时容易出现该轴段及附近轴段附加扭转力矩对其有较大相对灵敏度；而较小扭转刚度出现在系统中部时却不一定出现其所在轴段以及邻近轴段附加扭转力矩对其较大相对灵敏度数值的出现。不在动力传动路线上的轴段由于本身振动能量以及幅值较小，造成其附加扭转力矩对其他扭转刚度的相对灵敏度数值较大。

3.2 轴段附加扭转力矩对各点惯量相对灵敏度

与扭转刚度作为弹性储能元件不同，扭转振动系统中各质量点转动惯量是振动能量的直接体现，动力响应进行灵敏度分析时对各点转动惯量的灵敏度分析也是有实际意义的。图7中给出了各转速下系统中四段轴的附加扭转力矩对各质量点惯量的相对灵敏度结果。

从图7中可以看出轴段对各点惯量的相对灵敏度结果随转速的变化而发生变化，并不是一个定值。对（a）图中轴段1－2、（b）图中轴段21－22和（c）图中轴段25－26而言，不同转速下的各相对灵敏度数值在一定范围内变化，并没有数量级差异的情况出现。而（b）图中轴段21－22的附加扭转力矩对质量点22惯量的相对灵敏度在各转速下都为正值，相同的情况也发生在轴段29－31的附加扭转力矩对质量点31的相对灵敏度中。从图3可以看出质量点22和31分别为一轴左侧轴承和二轴右侧轴承且都不在动力的传动路线上，这说明为减小不在传递路线上的轴段振动能量和幅值应减小该轴段以及相关部件（如本文中质量点22 和31为轴承）的转动惯量。对（d）图中轴段32－33的结果分析发现其附加扭转力矩对大部分质量点惯量的相对灵敏度都在一个数量级上，但对J32、J29和J35的相对灵敏度较大。根据表2中各点惯量和表1中各扭转刚度的数据发现这几个点为惯量较大的质量点且kt32－33和kt33－35较小，故可以认为轴段附加扭转力矩对质量点惯量相对灵敏度较大是由较大的质量点和较小的扭转刚度共同作用形成。J32、J29和J35这几个惯量除了对轴段32－33和33－35的附加扭转力矩影响较大之外，对三轴上各轴段的附加扭转力矩影响也叫其它惯量大。相同的情况也发生在二轴上，由于kt25－26较小且J26较大，在动力传递路线上各轴段附加扭转力矩对J26相对灵敏度大于对其它惯量。

而不同轴段的相对灵敏度数值进行比较时，情况和上一节对扭转刚度的相对灵敏度分析类似，不在传递路线上的轴段21－22的附加扭转力矩对各点惯量的相对灵敏度数值大于在传递路线上轴段对相同惯量的相对灵敏度。

根据上面的分析知道大部分轴段附加扭转力矩对各点惯量的相对灵敏度在一个数量级上并随转速变化而变化，并且由于系统是一个整体，各部分之间互相影响造成同一轴段附加扭转力矩对不同惯量的相对灵敏度有正有负，并且即使同一相对灵敏度在不同转速下出现正值和负值都有可能。一个例外的情况出现于不在动力传递路线上轴段的附加扭转力矩对同样不在传递路线上的惯量的灵敏度始终是正值，这说明为减小该轴段的振动能量和幅值应减小相关的不在传递路线上部件的惯量。较大的相对灵敏度出现在附近扭转刚度较小且本身数值较大的惯量上，这种惯量对邻近且在动力传递路线上各轴段的附加扭转力矩影响都较大。

3.3 轴段附加扭转力矩对各齿轮副传动误差相对灵敏度

除了前面讨论的扭转刚度和惯量，研究动力学响应对轮齿啮合本身相关参数的相对灵敏度对系统减振的修改和优化有着更为直接的意义。图8中给出了各转速下四段轴的附加扭转力矩对系统中各齿轮副传动误差幅值的相对灵敏度。

通过对图3所示系统中各轴段附加扭转力矩对传动误差幅值的相对灵敏度图比较可以发现相对灵敏度图可以有五种形状结构。输入端所在轴段1－2、2－3 和3－4相对灵敏度图结构形状相同，如图8中（a）图所示；左输出端附近的轴段32－33和33－35的相对灵敏度图有相同结构形状，如（d）图所示；而右输出端附近轴段40－41和41－42由于扭转刚度比左输出端轴段大，其相对灵敏度图的结构与（d）图并不相同；还有就是不在动力传递路线上的轴段21－22、23－24和29 －31由于本身振动能量较小，具有较大的相对灵敏度数值且各点分布比较均匀，这说明各齿轮副误差对不在传递路线上轴段附加扭转力矩的影响比较接近；剩下的就是在传递路线上且不在系统输入输出端的轴段4－s1、s1－s2、c2－20、20－21、24－25、25－26、26－27、27－29、35－37、37－38、38－39和39－40，这12段轴的相对灵敏度图有相同结构形状，如（c）图所示。

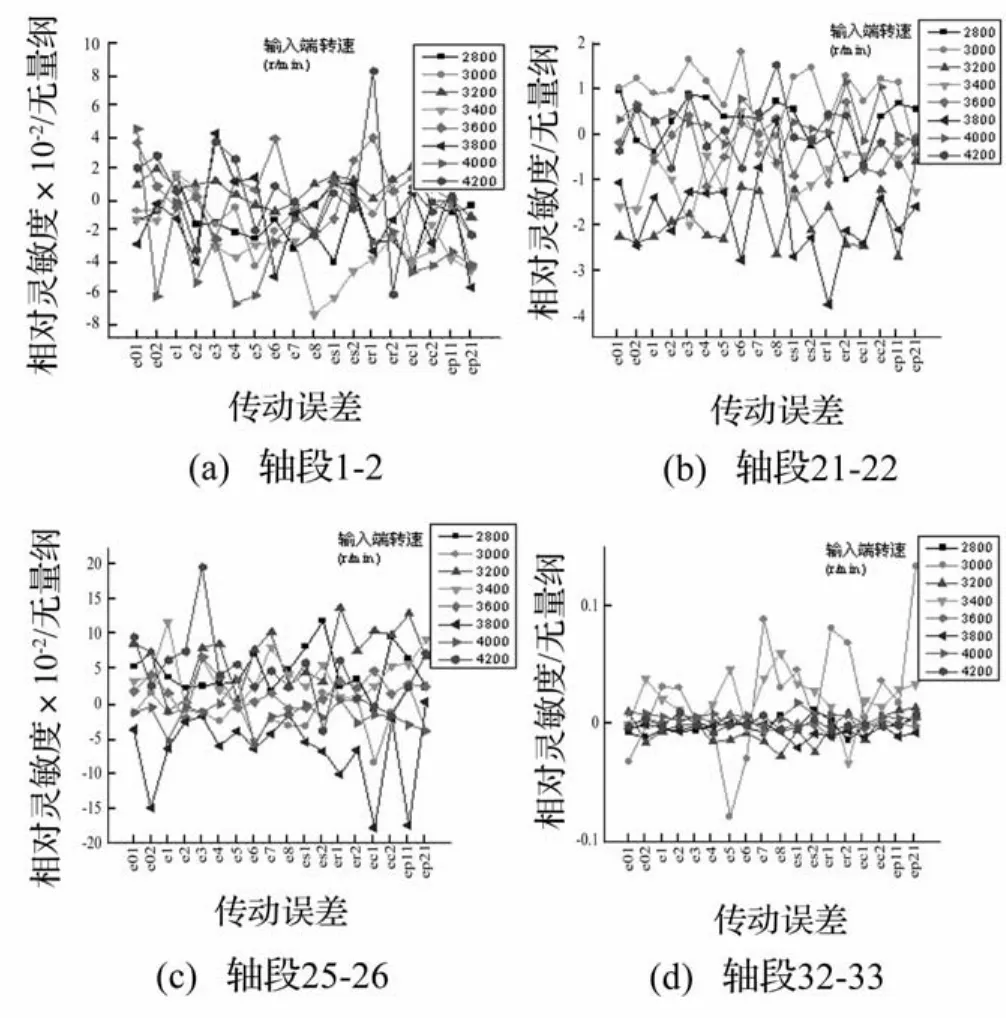
图8 各转速下轴段附加扭转力矩对传动误差幅值相对灵敏度Fig．8 The relative sensitivity of additional torque of shaft segments with respect to transmission error in different speed

对图8中各图进一步分析可以发现轴段附加扭转力矩对传力齿轮副误差的灵敏度不一定大于空转齿轮，在部分轴段上甚至小于对空转齿轮传动误差的相对灵敏度。而且随着转速的变化灵敏度数值有正有负，因此并不能简单的通过增加或减小齿轮精度的方法来达到减小轴段附加扭转力矩的目的。

3.4 轴承支反力对各齿轮副传动误差相对灵敏度

除了扭转方向上的附加扭转力矩，弯曲方向上的力对于齿轮箱的减振设计同样重要。其中，轴承支反力的大小直接决定了轴承座和箱体振动的动态特性。图9给出了各转速下系统中4处轴承支反力对各齿轮传递误差的相对灵敏度结果。

对系统中各轴承支反力对传动误差幅值的相对灵敏度图比较可以发现相对灵敏度图可以有五种形状结构。轴承1和轴承2的相对灵敏度结果图虽然数值不同但有类似的结构形状见图9（a）图所示，轴承2由于所受支反力较小，因此有较大的相对灵敏度数值，原因可以参见3．1节中对轴段21－22相对灵敏度的分析；轴承3、轴承4、轴承5、轴承7、轴承10和轴承11相对灵敏度结果图有类似的形状结构如（b）图所示，从图3中可以发现这6组轴承位于系统中定轴部分传力齿轮的两侧承受着较大的支反力；轴承8（（d）图）和轴承9位于三轴左侧输出端，它们相对灵敏度图的结构并不相同但有着较大的相对灵敏度，这说明三轴上大部分轴承支反力都由右侧的轴承10和11来承担；另外一个承担较大支反力的轴承是轴承6，其位于整个系统的中部，虽然承受较大的支反力但和其它6个位于传力齿轮两侧的轴承的结果图并不相同。

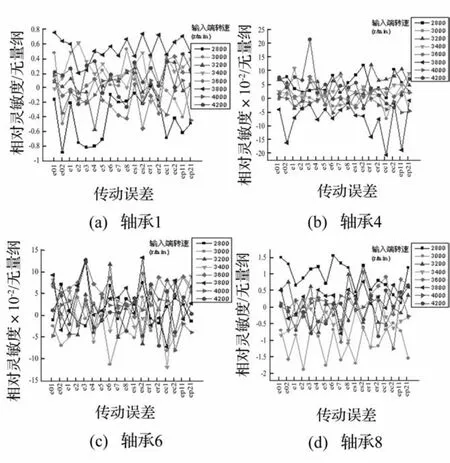
图9 各转速下轴承支反力对传动误差幅值相对灵敏度Fig．9 The relative sensitivity of support force of bearing with respect to transmission error in different speed

从上面的分析可以看出，轴承支反力对各传动误差的相对灵敏度图形结构同轴承在系统中的位置以及所受支反力的大小有关；另外根据相对灵敏度数值的大小也可以得出该轴承受力的大小情况，通常受力大的轴承相对灵敏度较小，受力小的轴承则反之；非线性系统中是否传力齿轮的传动误差对轴承支反力的影响并没有简单单一的规律，不能简单的给出定性的结论。

4 结 论

本文研究了包含时变啮合刚度、齿侧间隙、质量偏心和轮齿啮合误差等非线性因素的齿轮系统的响应对设计参数的灵敏度，并将其转化为工程中有实际意义物理量对设计参数的相对灵敏度结果，结论如下：

（1）非线性系统中响应对设计参数的灵敏度结果与转速相关、所处位置以及响应本身相关，相同类型的力矩／力有着类似的相对灵敏度图形结构，较大的响应对应着较大的响应灵敏度；

（2）不在动力传递路线上轴段的附加扭转力矩对同样不在传递路线上的惯量的灵敏度始终是正值，这表明为减小该轴段的振动能量和幅值应尽可能减小与其相邻且不在传递路线上的惯量；

（3）较大的惯量以及邻近轴段较小的扭转刚度是造成轴段附加扭转力矩对惯量相对灵敏度数值较大的原因。

［1］Chen C S，Natsiavas S，Nelson H D．Coupled lateraltorsional vibration of a gear-pair system supported by a squeeze film damper［J］．Journal of Vibration and Acoustics-Transactions of the ASME，1998，120（4）：860－867．

［2］Botman．Epicyclic gear vibations［J］．ASME J Eng Ind，1976，97：811－815．

［3］Saada A，Velex P．An extended model for the analysis of the dynamic behavior of planetary trains［J］．ASME Journal of Mechanical Design，1995，117：241－247．

［4］Lin J，Parker R G．Analytical characterization of the unique properties of planetary gear free vibration［J］．ASME Journal of Vibration and Acoustics，1999，121：316－321．

［5］Lin J，Parker R G．Sensitivity of planetary gear natural frequencies and vibration modes to model parameters［J］．Journal of Sound and Vibration，1999，228：109－128．

［6］Guo Y C，Parker R G．Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters［J］．Journal of Vibration and Acoustics，2010，132：011001－011013．

［7］张义民，闻邦椿，刘巧伶．动力响应灵敏度分析中的长期项消除［J］．振动工程学报，1998，11（4）：462－466．

ZHANGYi-ming，WENBang-chun，LIUQiao-ling．Elimination of secular terms from sensitivity analysis of dynamic responses［J］．Journal of Vibration Engineering，1998，11（4）：462－466．

［8］刘辉，蔡仲昌，曹华夏，等．车辆动力传动系统扭转强迫振动响应灵敏度研究［J］．兵工学报，2011，32（8）：939 －944．

LIU Hui，CAI Zhong-chang，CAO Hua-xia，et al．Sensitivity analysis of forced torsional vibration on vehicle powertrain ［J］．Acta Armamentarii，2011，32（8）：939－944．

［9］黄毅，刘辉，陈胤奇，等．车辆传动系统线性弯扭耦合振动响应灵敏度研究［J］．振动工程学报，2014，27（3）：333－340．

HUANG Yi，LIU Hui，CHEN Yin-qi，et al．Response sensitivity of the linear vibration of the gear system of the vehicle transmission［J］．Journal of Vibration Engineering，2014，27（3）：333－340．

［10］Zhao Y P，Kong J Y，Li G F，et al．Computerized simulation of tooth contact and error sensitivity investigation for ease-off hourglass worm drives［J］．Computer-Aided Design，2012，44（8）：778－790．

［11］Athervale S M，Gardner G D，Trent M．Sensitivity of transmissionnoiseandvibrationtomanufacturingand assembly process drift and variability［C］．Statistics and Analytical Methods in Automotive Engineering．2002：207 －216．

［12］Petrov E P．Method for sensitivity analysis of resonance forced response of bladed disks with nonlinear contact interfaces ［J］．Journal of Engineering for Gas Turbines and Power-Transactions of the ASME，2009，131（3）：（022510）1－9．

Response sensitivity of nonlinear translation-torsional vibration coupled model of a vehicle transmission system

HUANG Yi1，LIU Hui1，2，XIANG Chang-le1，2，YANG Zhi-gang1
（1．Beijing Institute of Technology，Beijing 100081，China；2．Vehicle Research Center，Beijing 100081，China）

With increase in requirements of dynamic quality of a transmission system，only the eigensensitivities analysis can not meet the requirements of dynamic characteristics of a vehicle transmission system．It's needed to do response sensitivity study to find a guideline to reduce vibration of a vehicle transmission system in designing stage．Here，the sensitivities of dynamic response with respect to design parameters such as，shaft torsional stiffness，moment of inertia，and transmission errors of gear pairs，et al．were investigated．The translation-torsional coupled dynamic model of a vehicle transmission system taking engine excitation as an input source was built up with the lumped parameter method．The sensitivity equations were derived from dynamic equations containing nonlinear terms，such as，time-varying mesh stiffness，backlash of gear pairs，mass eccentricity，transmission error et al．The relative sensitivities of dynamic response with respect to design parameters then turned into relative sensitivities of force／torque with respect to design parameters were acquired with the numerical simulation method．The results of the relative response sensitivities provided a theoretical basis for parameter modification，model updating and parameter optimization of vehicle transmission systems based on their dynamic responses．

vehicle transmission system；lumped parameter method；translation-torsional vibration coupled；nonlinear；response sensitivity

U461．1

A

10．13465／j．cnki．jvs．2014．23．017

国家自然科学基金（51375047）；教育部新世纪人才支持计划（NCET－12－0043）

2014－01－28 修改稿收到日期：2014－07－29

黄毅男，博士生，1982年生

刘辉女，教授，博士生导师，1975年生