多属性相对变权决策模型及方法
李春好,李孟姣,马慧欣,杜元伟,李金津
(1.吉林大学管理学院,吉林长春 130022;2.昆明理工大学管理与经济学院,云南昆明 650093)
多属性相对变权决策模型及方法
李春好1,李孟姣1,马慧欣1,杜元伟2,李金津1
(1.吉林大学管理学院,吉林长春 130022;2.昆明理工大学管理与经济学院,云南昆明 650093)
为克服多因素变权决策方法以及多属性决策Choquet积分模型没有科学反映多属性决策过程中决策者点依赖偏好关联行为的技术缺陷,在借鉴摆幅置权方法和网络分析法技术要点的基础上,运用数据包络分析的相对评价思维,提出一种全新的评价与决策方法即多属性相对变权决策方法。相对于多因素变权决策方法,新方法可以直接反映决策者的点依赖偏好结构,从而可以克服前者在反映点依赖偏好关联行为上所存在的源于决策分析者的武断随意性;相对于多属性决策Choquet积分模型,新方法可以反映决策者的点依赖偏好关联行为,并且在多数实际决策场合可以较有效地规避Choquet积分模型在决策参数判断上的指数复杂性难题。案例应用验证表明:新方法可以给出与决策者关于偏好依赖关联定性看法及客观事实非常相符的选择结论,可以更好地反映决策者的具体偏好。
多属性决策;变权决策;偏好依赖;摆幅置权;网络分析法;数据包络分析
1 引言
由于决策者关于属性的偏好通常并不能保证严格独立,因而建立在属性偏好独立假设基础上的传统多属性决策模型即属性权重相对方案单属性偏好保持不变的固权评价模型在解决实际问题的适用范围上受到了很大限制[1-3]。针对这一问题,学术界迄今提出了下述两种研究框架。
Sugeno等基于属性偏好关联提出了属性集模糊测度(fuzzy measure)概念,在此基础上Grabisch等[3]利用Choquet积分给出了属性关联条件下的多属性决策理论模型(下文简称作多属性决策Choquet积分模型)。从技术特点上看,该模型反映的是属性偏好之间相对于方案单属性偏好值排序而呈现出的偏好依赖关系即序依赖偏好关联关系。从理论和应用层面上来看,多属性决策Choquet积分模型目前尚存在如下两方面不足。其一,它只能够反映序依赖偏好关联关系,不能够更精细地反映相对方案单属性偏好值不同而不同的点依赖偏好关联关系。其二,属性集模糊测度的确定会遇到指数复杂性限制,对于属性个数为n的多属性决策问题,需要决策者通过判断给出的决策参数即属性集模糊测度为2n-2个,因而对于属性较多的决策问题往往会因决策者不能开展指数量级的判断工作而使模型失去应用的可行性[4-5]。
与上述的研究框架不同,基于经验性观察Zhang等[6]提出了属性权重应随方案单属性偏好值变化而变化的多属性变权决策思想。在此基础上,通过公理化定义属性变权与属性状态变权,Li Hongxing[7-9]带领的研究团队以“由因素(即属性)的固权生成因素的变权”的技术路线,建立了属性权重随属性值及其偏好变化而变化的多因素变权决策方法。尽管从形式上看该方法相对于多属性决策Choquet积分模型可以反映点依赖偏好关联关系,但从本质上讲关于多因素变权决策分析的关键即如何选择状态变权向量表达式中的参数以体现实际问题的变权机理、恰当反映决策者的偏好行为,学术界迄今尚未给出较为合理有效的技术方法。目前确定状态变权向量的方法无论是乐观系数法[8]、调权水平法[9]还是态度因子法[10],均没有从理性层面上描述出其中需由决策分析者予以选定的参数值与决策者实际偏好结构之间的明确对应联系,因此在状态变权向量的确定上尚存在着明显的武断随意性。
综上所述易见,就如何科学反映多属性决策过程中决策者所呈现出的点依赖偏好关联行为,迄今尚缺乏支持科学决策的有效方法。为克服这方面的研究不足,下文在借鉴摆幅置权方法[1](SW—Swing Weighting)和网络分析方法[11](ANP—Analytic Network Process)有关技术要点的基础上,运用数据包络分析[12](DEA—Data Envelopment A-nalysis)的相对评价思维,提出一种旨在科学合理反映决策者相对方案单属性偏好不同而不同的点依赖偏好关联行为的新评价与决策方法,即多属性相对变权决策方法。
2 基础知识准备与相关研究评析
2.1 多属性固权决策方法
设多属性决策问题共有M个备选方案,分别记为Ak,k=1,…,M,需要分析的属性因素分别为C1,…,Cn;任意一个决策方案A在C1,…,Cn上的属性值记为x1,…,xn,方案Ak在属性因素Ci上的状态值记为xi,k,则经典多属性固权决策模型的表达式为:
其中,Uk为决策者对第k个方案Ak的综合偏好;Vi,k=wiui(xi,k);ui(xi,k)为决策者对方案Ak在属性因素Ci上的状态值xi,k所给出的单属性偏好,ui(xi,k)∈[0,1];wi为决策者基于对总目标偏好贡献的视角对单属性偏好ui(xi,k)所判断给出的权重,0≤wi≤1,,并且相对xi,k以及ui(xi,k)的变化,wi保持固定不变[1-2]。因此,式(1)又被称为多属性决策的固权综合决策模型。
若对于x1,…,xn总存在与式(1)相联系的综合价值函数,则称属性C1,…,Cn之间偏好绝对独立或简称为属性偏好独立[2]。显然,当属性偏好不能满足独立条件时,采用式(1)进行多属性方案选择并不能够保证决策结论具有科学合理性。Winterfeldt和Edwards[1]为保证属性权重具有合理的内涵解释,给出了关于属性权重wi赋值的SW方法。不失一般性,设单属性偏好函数ui(xi)∈[0,1]为非减函数,i=1,…,n,则SW方法可以概括为如下几个步骤。首先,定义两个虚拟的锚点(Anchor-point)方案,即最差虚拟方案AL和最理想虚拟方案AH,其中:
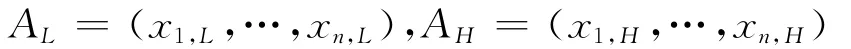

并且由ui(xi)∈[0,1]的函数非减性易知,ui(xi,H)=1和ui(xi,L)=0。然后,让决策者进行关于(Vi,H-Vi,L)/(Vf,H-Vf,L)的主观偏好比率判断(下文将该种判断模式称为SW判断)并将得出的判断值记为βi,f。其中,Vf,H-Vf,L为决策者首先希望在第f(f∈{1,…,n})属性上将AL的属性值改进为AH的属性值所带来的偏好变化;Vi,H-Vi,L为决策者在第i(i=1,…,n)属性上将AL的属性值改进为AH的属性值所带来的偏好变化。最后利用决策者判断给出的偏好比率值βi,f,并结合式(1)以及ui(xi,H)=1和ui(xi,L)=0,得出如下所示的属性权重:

2.2 多因素变权决策方法
针对多因素决策问题,Li Hongxing等[7]在承认属性因素固权存在即承认属性偏好独立的前提下给出了如下式(3)所示的多因素变权综合决策模型。

式(3)中,xi,k与ui(xi,k)的含义同前,ui(xi,k)∈[0,1];U′k为方案Ak的综合评价值;wi(x1,k,…,xn,k)为属性因素Ci(相对方案Ak)的变权,并且wi(x1,k,…,xn,k)需满足规一化条件…,xn,k)=1。若将属性偏好独立条件下属性因素Ci的固权权重仍记为wi,记状态向量X=(x1,…,xn),S(X)=(S1(X),…,Sn(X))为X的状态变权向量,则式(3)中的属性变权即wi(X)须由下式(4)予以确定:

在多因素变权综合决策方法中,若wi(X)相对xi单调递增(递减)则被称为激励型变权(惩罚型变权)。由式(4)易知,如何科学确定出状态变权向量S(X)是应用多因素变权综合决策方法的关键所在。目前,确定状态变权向量S(X)主要有乐观系数法、调权水平法和态度因子法[8-10]。其中,乐观系数法通过乐观系数(α)来确定S(X)。其表达式为

2.3 ANP方法
Saaty[13]提出的ANP方法是为了反映评价与决策问题中元素之间依赖(偏好依赖)关系而对层次分析方法(AHP—Analytic Hierarchy Process)的发展。其主要分析步骤依次为:对决策问题构建由元素集组成、反映元素集及其元素之间依赖关系(及反馈关系)的网络分析结构;基于该结构邀请专家或决策者主观判断给出决策问题的超矩阵或加权超矩阵;对构造出的超矩阵或加权超矩阵求极限并由此得出各个元素集和元素的极限排序权重(向量)[11]。
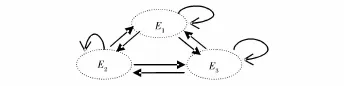
图1 ANP网络分析结构
特别地,参见图1所示的ANP网络分析结构,当决策问题由1个元素集构成并且该元素集有3个元素时,ANP要求决策者给出的超矩阵Q具有式(6)所示的结构形式。
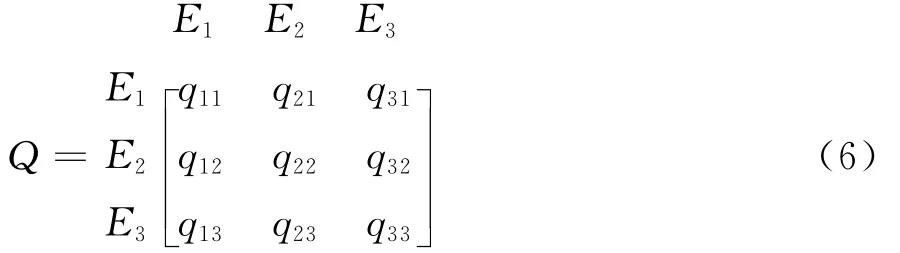
i=1qji=1(∀j=1,2,3),超矩阵Q因此为列随机矩阵。基于该矩阵特点ANP指出,当Q+∞存在时,Q+∞为列相等矩阵,其列向量即为决策问题各元素的极限排序权重。当Q+∞不存在时,极限排序权重向量需要用Cessaro和予以求出[11]。
分析上述超矩阵构造所采用的主观偏好判断模式可以看出,其中需要采用一种 “相对于甲来比较甲和乙”的特殊判断逻辑。一些专家学者如Feng Chengmin等[15]和Wu Weiwen[16]认为决策者按照上述逻辑进行主观偏好判断是极其困难的。基于这方面考虑,后文在应用ANP构建新决策方法时将给出一种不依赖上述特殊逻辑的超矩阵构建手段。
2.4 DEA方法
DEA是由Charnes、Cooper和Rhodes[12]所提出的旨在评价决策单元相对效率的一种定量分析方法。若决策单元DMUk是仅有产出而无投入的决策单元,其产出向量为dk=(dk1,…,dkn)>0,k= 1,…,M,其中dki为DMUk第i个产出的指标值,i =1,…,n,则对DMUo(o=1,…,M)而言的DEA模型可以表示为:
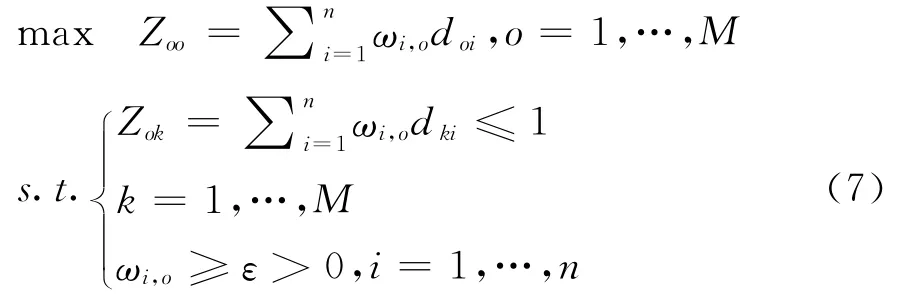
其中,ε为非阿基米德无穷小;ωi,o为第i个产出的虚拟权重(或虚拟价格),i=1,…,n,并且它们被统称为决策单元的虚拟权重体系;Zoo的最优值称为DMUo的相对效率评价值,∀o=1,…,M。
设式(7)关于ωi,o的最优解向量即最优虚拟权重体系为(ω,…,ω),则由于它使得Zoo取最优值即令DMUo相对效率最大化,因而是最有利于DMUo的虚拟权重体系[17]。由此可知,Zok是在最有利于DMUo的最优虚拟权重体系下DMUk的相对效率评价值,∀k=1,…,M。
Dyson和Thanssoulis[18]、Wong和Beasley[19]等建议在式(7)的约束条件中引入权重置信域(AR—assurance region)以约束虚拟权重的取值范围,并将引入权重置信域的DEA模型称作DEA/ AR模型。特别地,Wong和Beasley[19]从多属性决策视角将决策单元在两个指标上的虚拟价值(即虚拟权重与指标值的乘积)之比解释为相应指标的单属性偏好值之比,在此基础上建议利用决策者关于单属性偏好值之比的偏好判断信息来构建出DEA的权重置信域。另外,从理论上讲DEA/AR模型特别是DEA并不能保证最优虚拟权重体系即最优解向量的唯一性。为此,学术界提出了激进型求解策略[17]、仁慈型求解策略[17]、中立性求解策略[20]等多种技术方法。因此,在后文采用DEA技术建构有关决策模型时,不妨假定其中涉及到的DEA/AR模型存在唯一最优虚拟权重体系。
3 模型构建
若我们在SW判断中不改变最差锚点方案AL而将方案Ak视为最理想锚点方案,那么对任意一个备选方案Ak而言,SW判断对由备选方案Ak和最差锚点方案所组成的方案对仍然适用。因此对于备选方案Ak和最差锚点方案AL,可以让决策者进行关于(Vi,k-Vi,L)/(Vfk,k-Vfk,L)的主观偏好变化比率判断,其中,Vfk,k-Vfk,L为决策者首先希望在第fk(fk∈{1,…,n})属性上将AL的属性值改进为Ak的属性值所带来的偏好变化量,Vi,k-Vi,L为在第i属性上将AL的属性值改进为Ak的属性值所带来的决策者偏好变化量,i=1,…,n。设关于(Vi,k-Vi,L)/(Vfk,k-Vfk,L)决策者所给出的偏好变化比率判断值为β,wi,k为基于决策者对方案Ak和AL的SW判断信息所确定出的第i个属性Ci的权重,则由式(1)和ui(xi,L)=0可知:对于方案对Ak和AL而言,
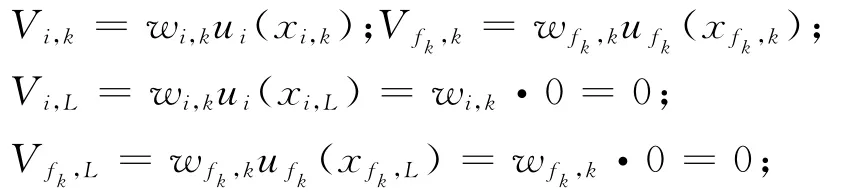
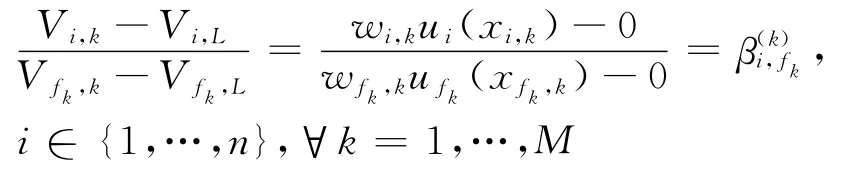
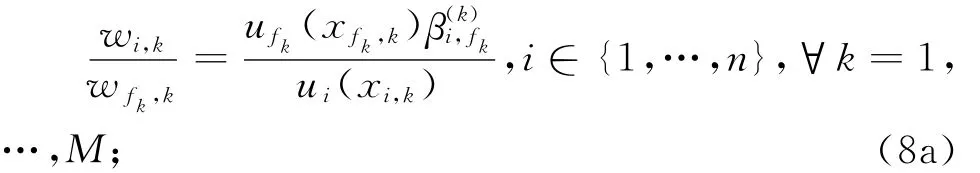
wi,k∈R,i∈{1,…,n},∀k=1,…,M (8c)
由式(8a)、(8b)和式(8c)可知,属性权重之比(如wi,k/wfk,k)或属性权重并非总能够满足多属性固权综合模型属性权重的内在性质要求,即属性权重之比或属性权重在偏好独立的假设条件下相对备选方案的变化而保持固定不变。特别地,由式(8a)可知,属性权重之比wi,k/wfk,k归根结底是xi,k、的函数,因而一般说来它既会随方案Ak各个属性值的变化而呈现出非线性函数变化,也会随决策者关于方案Ak各个属性值的偏好关联关系(体现为)的变化而变化。
由于属性值x1,…,xn是方案A在各个属性上的特征描述,因此当决策者对属性的偏好存在关联关系即属性偏好关联依赖时,决策者对各个备选方案的偏好也是关联依赖的。这表明人们可以从ANP的分析视角将多属性决策问题的备选方案集视为一个ANP元素集,将各个备选方案视为彼此之间(包括自己与自己之间)相互影响并且这种相互影响可以由偏好关联依赖关系和ANP超矩阵予以表示的ANP元素。有鉴于此,对于拥有M个备选方案、属性偏好关联的多属性评价问题,我们可以将它表示为系统结构与图1类似、含有1个元素集并且元素集中有M个元素的ANP评价问题。类似于式(6),其对应的ANP超矩阵为:
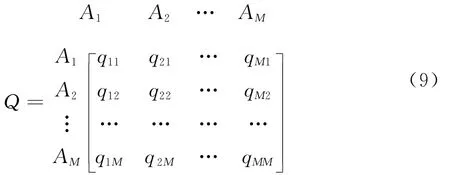
其中,第j列矩阵元素的含义为相对于备选方案Aj而言决策者对备选方案A1,A2,…,AM的相对偏好程度,它们满足
下面在借鉴DEA技术的基础上,通过对ANP超矩阵构建所采用的比较逻辑的理性解释,给出一种能够反映决策者主观偏好比率判断信息(i∈{1,…,n},∀k=1,…,M)的超矩阵Q的构建方法。
以式(9)的第j列矩阵元素为分析对象,在确定这些矩阵元素的取值时,ANP要求决策者主观判断回答的是相对于备选方案Aj而言他对备选方案A1,A2,…,AM的相对偏好程度。从理性上讲,这实际上是允许决策者选择出一种最有利于、最适宜于方案Aj的权重体系并采用该体系来评价方案A1,A2,…,AM的偏好值以及它们之间的相对偏好值。按照这一解释并结合DEA的技术特点(参见前文2.4),我们便可以利用DEA技术来识别出最有利于方案Aj的虚拟权重体系,并在此基础上利用DEA/AR分析技术识别出最有利于且最适宜于方案Aj的虚拟权重体系。
从DEA分析的视角上看,多属性决策方案Aj是一个仅有产出、没有投入的决策单元,其中决策单元Aj的第i产出为它在属性Ci上的单属性偏好函数值ui(xi,j)。由此参见式(7),可以建构如下DEA分析模型。

求解该线性规划模型,即可以得出最有利于方案Aj的虚拟权重体系{|i=1,…,n},j=1,…,M。但是,该权重体系并非一定适合于决策者对方案Aj具体属性特征的偏好看法(即)。
借鉴Wong和Beasley[19]的虚拟权重置信域构建思想可知,决策单元即方案Aj相对于AL在产出i上的虚拟价值变化即是Aj相对于AL在属性Ci上的偏好值变化,因此当≥0且ui(xi,j)≠0时有:
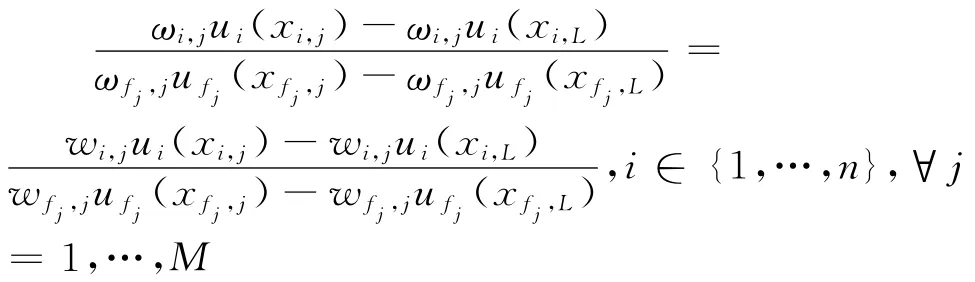
由此并结合ui(xi,L)=0和ufj(xfj,L)=0可知:
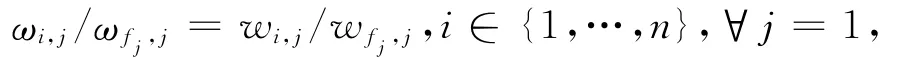

这样,结合式(8a)和式(8b)便可以构建出如下最适宜于方案Aj(即能够反映决策者关于方案Aj所给出的判断信息)的DEA虚拟权重置信域。即:

将上述最适宜于方案Aj的DEA虚拟权重置信域添加到式(10)的约束条件之中,可以得出如下DEA/AR模型。

求解该线性规划模型,便可以得出最有利于且最适宜于方案Aj的虚拟权重体系{ω*i,j|i=1,…,n},j=1,…,M;对应于权重体系{ω*i,j|i=1,…,n},方案A1,A2,…,AM的综合偏好值分别为Z1,j,…,ZM,j,j=1,…,M。利用这些偏好评价值便可以得出A1,A2,…,AM在权重体系{ω*i,j|i=1,…,n}下的相对偏好值(即相对Aj而言决策者对A1,A2,…,AM的相对偏好程度)qjt。其具体表达式为:


其中,I=(1,1,…,1)T为M维列向量。当极限超矩阵Q+∞不存在时,由于Q为列随机矩阵,因此一定存在循环周期c(c为正整数)使得存在[11]。此时利用Cessaro和可以得出[11]:

在此基础上,决策者可以利用式(14)或(15)给出的优选排序权重向量(δ1,δ2,…,δM)筛选出一个优选排序权重值最大的方案或几个优选排序权重值较大的方案做为最终的决策选择。
由超矩阵Q的构建过程可以看出,其中采用的主观偏好比率信息,i∈{1,…,n},∀j=1,…,M,实质上反映的是随待评方案Aj变化而变化的权重ω1,j,…,ωn,j之间的比率。因此,由式(14)(或式(15))及其依赖的式(12)、式(13)和式(9)所构成的决策模型,是一种所使用的虚拟权重体系相对于待评方案变化而变化、因而可以反映点依赖偏好关联关系的多属性变权决策模型。另外,除(i∈{1,…,n})之外,结合式(14)(或(15))及其依赖的式(12)可以看出,δj依赖的虚拟权重体系还要受到ui(xi,k)(i=1,…,n;k=1,…,M)即归根结底要受到备选方案集{Ak|k=1,…,M}的影响。由此可知,与DEA效率评价的本质即相对评价类似,由式(14)(或式(15))及其依赖的式(12)、式(13)和式(9)所构成的决策模型,归根结底也是一种虚拟权重体系相对于备选方案集变化而变化的相对评价模型。综合以上两方面的模型特点,我们将由式(14)(或式(15))及其依赖的式(12)、式(13)和式(9)所构成的决策模型称为多属性相对变权决策模型。
需要特别指出,相对于多因素变权决策方法在状态变权向量确定上所存在的、源于决策分析者的武断随意性问题而言,该模型依赖的偏好信息即均由决策者给出,因而可以直接反映决策者的偏好结构;相对于多属性决策Choquet积分模型,该模型具有精细反映点依赖偏好关联关系的技术优势。此外,由于多属性相对变权决策模型要求决策者判断给出的偏好比率为M(n-1)个,因而一般说来当决策属性多、备选方案不多时其要求决策者判断给出的参数会远小于多属性决策Choquet积分模型所需要确定的属性集模糊测度的个数即2n-2。由于实际的多属性决策问题往往具有决策属性多但备选方案不多的系统特征,因而多属性相对变权决策模型在多数的实际决策场合可以较有效地规避多属性决策Choquet积分模型关于属性集模糊测度判断的指数复杂性难题。尽管有的多属性决策问题仅具有少数几个决策属性,但我们不能因此而否定现实管理实践中具有决策属性多但备选方案不多系统特征的决策问题的存在。由此可以保守地讲,多属性相对变权决策模型至少也是多属性决策Choquet积分模型的重要补充。
还需要强调指出,关于多属性相对变权决策模型依赖的变权思想,即对同一个多属性决策问题的不同方案在计算优劣排序权重δj时潜在使用的可能是数值不同的属性权重组,其科学合理性,可以从如下两方面予以解释。其一,上述变权思想已在现有的多因素变权决策方法中予以了采用(参见式(5)易知该方法对不同方案予以不同状态变权并且由此结合式(4)可知对不同方案可予以不同的属性权重组),其科学合理性由文献[6-10]可知已为学术界所认可(注:本文支持现有多因素变权决策方法的变权思想但不支持其中的具体变权作法)。其二,上述变权思想,从哲学层面上讲正是“具体问题、具体分析”的辩证分析观在决策实践上的具体体现,即对于具体方案予以具体分析,因而具有可靠的哲学基础。
从理论上讲,多属性相对变权决策模型给出的评价结论会随着备选方案集的变化而出现逆序现象。尽管部分关于多属性决策的已有常用方法如AHP、优劣解距离法(TOPSIS[21])等均会出现逆序现象[22],并且因此它们的科学合理性受到了学术界的质疑,但该现象的出现对于多属性相对变权决策模型而言并不意味着模型存在理论缺陷。其中原因在于:当属性偏好关联依赖时备选方案之间也是偏好关联依赖的(关于这一点请参见前文),因而在属性偏好独立假设下要求决策方法不出现逆序现象的必要条件即方案之间偏好独立,对于旨在揭示属性偏好关联依赖关系的多属性相对变权决策模型而言已不再适用。
最后有必要指出,多属性相对变权决策模型仍然可以保证多属性决策理论关于偏好序的基本公理假设,即存在下述定理。
定理1 对于决策方案集{Ak|k=1,…,M}中任意两个属性值向量为Xa和Xb的方案,若Xa≤Xb,则多属性相对变权决策模型对它们所给出的优选排序权重δa、δb恒满足δa≤δb。
证明:设Xa和Xb对应的单属性偏好值向量分别为(u1,a,…,un,a)、(u1,b,…,un,b)。由于Xa≤Xb,因此结合单属性偏好函数的非减性易知(u1,a,…,un,a)≤(u1,b,…,un,b)。由此并结合式(12)的第一组约束条件可知,Za,j≤Zb,j,j=1,…,M,进而由式(13)可知qja≤qjb,j=1,…,M。由此,结合矩阵相乘的数学知识由式(14)(或式(15))可知δa≤δb。证毕。
4 多属性相对变权决策的方法步骤
步骤1:基于备选方案集{Ak|k=1,…,M}构造出虚拟最差方案AL并让决策者分别以最差方案AL和待评方案Aj为锚点方案,运用SW判断给出属性C1,…,Cn中其首先希望将AL的属性值改进为Aj的属性值的那个属性,并将该属性记为属性fj,fj∈{1,…,n};然后,以属性fj为比较基准给出主观偏好比率判断值,i=1,…,n;j= 1,…,M。
步骤2:请决策者对备选方案Ak在属性C1,…,Cn上属性值的单属性偏好ui(xi,k)予以判断赋值,其中i=1,…,n,k=1,…,M。由单属性偏好函数ui(xi)的非减性和ui(xi,L)=0可知:当备选方案集中某个方案在各个属性上单属性偏好均为0时,该方案必是与最差方案等价、无需再采用评价模型予以评价的最劣方案,因而这里不妨假定{Ak|k=1,…,M}中的每个方案至少在一个属性上的单属性偏好不为0。
步骤4:利用式(13)和步骤3得出的Z1,j,…,ZM,j,计算得出qjt,其中t,j=1,…,M;在此基础上利用式(9)构造出超矩阵Q。
步骤5:利用式(14)(或(15))得出方案Ak的优选排序权重δk,k=1,…,M;在此基础上筛选出一个优选排序权重值最大的方案或几个优选排序权重值较大的方案做为最终的决策选择。
5 多属性相对变权决策方法的实证分析
现有某大学管理科学与工程专业5名高年级大学生(视为备选方案Ak;k=1,2,…,5)提出了该专业推免硕士研究生的报名申请。根据有关规定,该硕士点的负责人(视为决策者)需要从学生大学阶段数学平均成绩(百分制)、英语六级成绩(折算为百分制)和已修专业课的平均成绩(百分制)三方面(依次视为属性C1、C2、C3)优选出3名学生进入面试。5名学生在3个属性上的属性值即xi,k(i=1,2,3;k =1,…,5)如下表1所示。
由于决策者在评价决策过程中可能在C1、C2、C3上存在偏好依赖关联关系,因此在让决策者给出其具体数值偏好信息之前,首先关于属性上是否存在偏好依赖关联关系向决策者做出了两方面定性调查。决策者对定性调查所做出的回答为:(1)当学生的数学成绩或英语成绩特别好时,专业课的成绩可以差一些;(2)当学生的数学成绩和英语成绩均比较差时,即使学生的专业课成绩非常好也不应获得较高的综合评价结论。由上述回答可以看出,决策者关于方案的属性值存在偏好依赖关联关系,因此下文采用前面给出的多属性相对变权决策方法来对学生的优选予以决策支持。
根据多属性相对变权决策的方法步骤,决策者经偏好判断分别给出了如表2(其中AL=(60,70,80))所示的主观偏好比率和如表3所示的各个方案的单属性偏好值。将表2和表3的数据信息代入到式(12)可以得到如表4所示的综合偏好评价值Zt,j,t,j=1,…,5。

表1 方案Ak的属性值
表2 决策者判断给出的主观偏好比率
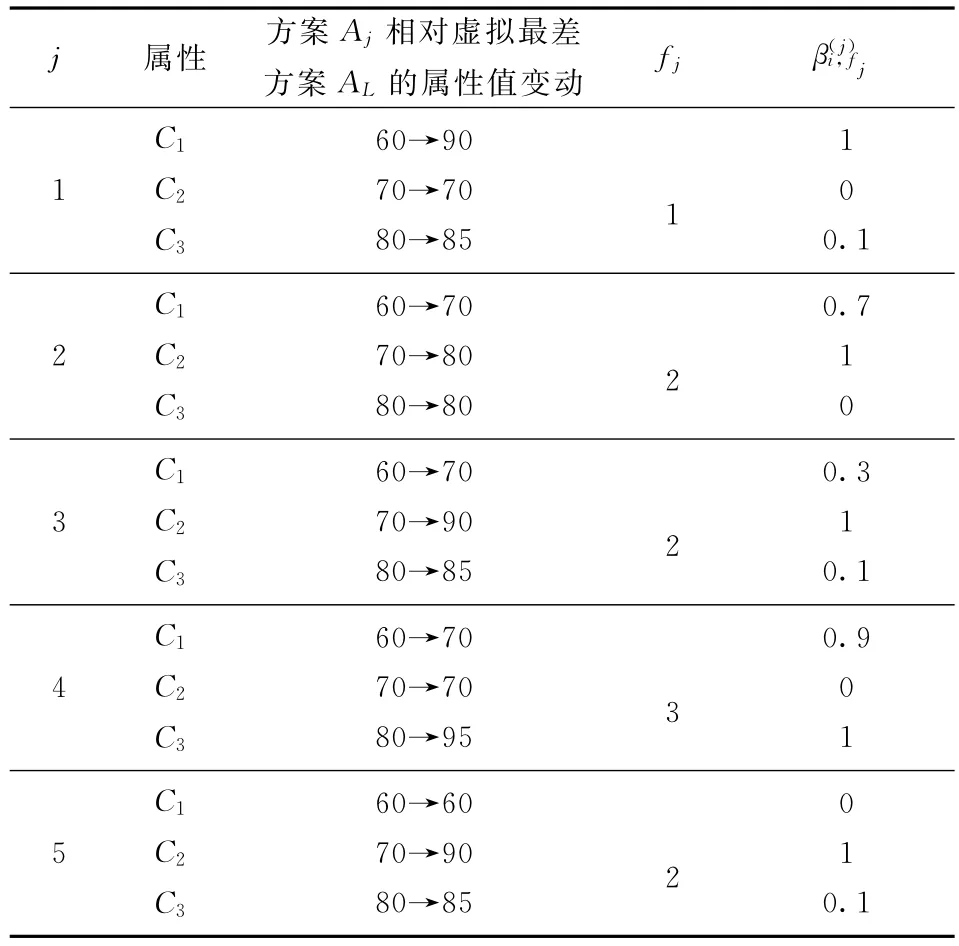
表2 决策者判断给出的主观偏好比率
j 属性 方案Aj相对虚拟最差方案AL的属性值变动 fjβ(j)i,fj 1 C1C2C3 60→90 70→70 80→85 1 10 0.1 0.7 2 C1C2C3 60→70 70→80 80→80 2 1 0 3 C1C2C3 60→70 70→90 80→85 2 0.3 1 0.1 0.9 4 C1C2C3 60→70 70→70 80→95 3 0 1 5 C1C2C3 60→60 70→90 80→85 2 01 0.1

表3 方案Ak在属性C1、C2、C3上的单属性偏好

表4 模型最优解Zt,j

表5 超矩阵Q的元素值
基于表4和式(13)及式(9)得出的反映方案之间偏好依赖的超矩阵Q如表5所示。由超矩阵Q按照式(14)计算得出学生A1,A2,…,A5的优选排序权重向量(δ1,δ2,δ3,δ4,δ5)为:
(0.3665,0.1624,0.1961,0.1171,0.1579)
由此可知,A1,A2,…,A5的优选排序为:

据此决策者应选择A1、A3、A2进入下一轮面试。
参见表1,A3、A5仅在数学成绩上存在差异并且A3的数学成绩优于A5,这客观上表明无论属性偏好依赖与否,进行综合评选都必有A3优于A5。将前面得出的优选排序权重结果与这一事实相比可以发现,多属性相对变权决策方法对学生A3和A5所给出的排序正如定理1所言与客观事实完全相符。结合A1、A3在各科上的具体成绩特征(即专业课成绩虽然一般但他们要么数学成绩特别好要么英语成绩特别好),可以看出多属性相对变权决策方法将A1、A3排在优选排序的前两位与前文决策者给出的定性看法(1)具有高度的相符性。另外,A4、A5的总成绩虽然相同,但结合他们在各科上的成绩特征(即A4的数学成绩和英语成绩均比较差但其专业课成绩特别好、A5尽管在专业课成绩一般并且数学成绩特别差但其英语成绩特别好)可以发现:多属性相对变权决策方法关于A4、A5所给出的优选排序A5≻A4,与前文决策者给出的定性看法(2)及定性看法(1)也非常相符。最后结合式(16)易知,多属性相对变权决策方法关于A4所给出的优劣排序位置也与决策者的定性看法(2)明显相符。上述四方面表明,多属性相对变权决策方法是合理有效的。
下面开展多属性相对变权决策方法与多因素变权决策方法及多属性固权决策方法的实证对比分析,以进一步验证多属性相对变权决策方法的科学合理性。由于多属性固权决策方法和多因素变权决策方法在应用中需要引入异于多属性相对变权决策方法的偏好信息判断模式,因此为了保证方法比较的偏好信息可比,这里采用近似拟合手段,基于前文由多属性相对变权决策方法对A1、A2、…、A5所得出的优选排序权重,对多属性固权决策方法和多因素变权决策方法需要使用的固权权重予以最优估计。其中依赖的是一种趋向于夸大多属性固权决策方法功效(或贬低多属性相对变权决策方法功效)的技术思想,即由最优估计得出的固权权重能够尽可能使信息结构相对简单的多属性固权决策方法得出与信息结构相对复杂的多属性相对变权决策方法相近的方案评价排序结论。由此从方法科学合理性验证上看,若多属性固权决策方法或多因素变权决策方法优于多属性相对变权决策方法,那么前两种方法采用由上述拟合手段得出的固权权重去评价A1,A2,…,A5,便至少不能给出劣于后者的评价结论;否则便说明后者在科学合理性上优于前两者。关于固权权重的具体最优估计模型为:

式(17)中,wi为待拟合的属性C1、C2、C3的固权权重,wi≥0,i=1,2,3;εi为拟合误差;a和b分别为依据偏好效用理论所设置的线性变换待定常数(其中b≥0保证的是同向偏好效用变换);F为优化控制的目标函数;Bi为保证最优估计模型具有二次规划数学结构所引入的定义变量(Bi=bwi),并且由b≥0和wi≥0(i=1,2,3)可知Bi≥0,i= 1,2,3。

将上面得出的固权权重(即w1、w2和w3)值和表2中方案Ak在各个属性上的单属性偏好值代入到多属性固权决策方法的表达式(1)中可得:U1= 0.7029,U2=0.2657,U3=0.2982,U4=0.3073,U5=0.2283。由此可知,各方案的优劣排序为:

由此排序可以看出,多属性固权决策方法并没有较好地反映出决策者的定性偏好看法,例如,对数学成绩和英语成绩均比较差的A4,该方法给出了与决策者定性看法(2)明显不符的排序结论。由此并结合前述多属性相对变权决策方法应用所得结论(或结合式(16)和式(18)中关于A4的排序位置差异)可知:多属性相对变权决策方法相对于多属性固权决策方法,在反映决策者具体偏好看法上具有明显的比较优势。
依据属性C1、C2、C3的固权权重值,利用关于状态变权的式(4)和多因素变权决策方法,可得出该方法在参数α取不同数值时对方案所给出的综合评价值(具体结果见表5)。由表5可知,在参数α取值大于10时,多因素变权决策方法给出的方案排序仅是趋向将多数方案等同看待而已,因而其对方案优劣的区分能力较差。在参数α取值小于等于10时,多因素变权决策方法与多属性固权决策方法给出的方案排序结论非常类似,对数学成绩和英语成绩均比较差的A4,多因素变权决策方法同样给出了与决策者定性看法(2)明显不符的排序结论。由此并结合前述多属性相对变权决策方法应用所得结论可知:即使在参数α取值能够保证多因素变权决策方法具有较好方案优劣区分能力的条件下,多属性相对变权决策方法相对于多因素变权决策方法,也在反映决策者具体偏好看法上具有明显的比较优势。

表5 在α取不同数值时多因素变权方法对方案所给出的综合评价值
6 结语
多属性固权决策方法由于否定了现实决策中决策者在属性偏好上可能存在的关联依赖关系,因而在解决实际问题的适用范围上受到了很大限制。而为解决该问题所提出的多属性决策Choquet积分模型一方面不能反映决策者的点依赖偏好关联行为,另一方面还要受到属性集模糊测度确定的指数复杂性限制。多因素变权决策理论方法虽然试图解决多属性固权决策方法相对属性值及其偏好的变化而保持属性权重固定不变的理论不足,在形式上可以反映决策者的点依赖偏好关联行为,但该方法却存在着需要决策分析者主观武断选择变权参数的明显缺陷。本文针对上述已有相关研究的不足,在借鉴SW方法和ANP方法有关技术要点的基础上,运用DEA的相对评价思维及建模技术,提出了一种全新的评价与决策方法即多属性相对变权决策方法。其技术优势在于:其一,相对于多因素变权决策方法,它可以直接反映决策者的点依赖偏好结构,从而可以规避多因素变权决策方法在状态变权向量确定上所存在的、源于决策分析者的武断随意性问题。其二,相对于多属性决策Choquet积分模型,它既可以精细地反映决策者的点依赖偏好关联关系,也可以在多数的实际决策场合较有效地规避多属性决策Choquet积分模型在属性集模糊测度判断上所存在的指数复杂性难题。案例应用验证表明:多属性相对变权决策方法可以给出与决策者关于偏好依赖关联定性看法及客观事实非常相符的选择结论;多属性相对变权决策方法相对于多属性固权决策方法和多因素变权决策方法可以更好地反映决策者的具体偏好,从而具有更强的科学合理性。但是应当指出,任何新决策方法的科学有效性都不能仅通过一次成功的案例应用加以充分证实(在国内外关于新决策理论方法的研究中正是由于这个原因才通常仅给出新理论方法的算例说明)。这显然对多属性相对变权决策方法也不例外,其进一步科学有效性尚需要大量实践应用的验证。
[1]Winterfeldt D V,Edwards W.Decision analysis and behavioral research[M].Cambridge:Cambridge University Press,1986.
[2]Keeney R L,Raiffa H.Decision with multiple objectives:preference and value tradeoff[M].New York:Wiley,1993.
[3]Grabisch M,Labreuche C.A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid[J].Annals Operations Research,2010,175:247-286.
[4]Kojadinovic I.Estimation of the weights of interacting criteria from the set of profiles by means of informationtheoretic functionals[J].European Journal of Operational Research,2004,155(3):741-751.
[5]章玲,周德群.基于k-可加模糊测度的多属性决策分析[J].管理科学学报,2008,11(6):18-24.
[6]Zhang D,Yu P L,Wang P Z.State-dependent weights in multicriteria value functions[J].Journal of Optimazation Theory and Application,1992,74(1):1-21.
[7]Li Hongxing.Fuzzy decision making based on variable weights[J].Mathematical and Computer Modelling,2004,39(2-3):163-179.
[8]李德清,李洪兴.状态变权向量的性质与构造[J].北京师范大学学报(自然科学版),2002,38(4):455-461.
[9]李德清,李洪兴.变权决策中变权效果分析与状态变权向量的确定[J].控制与决策,2004,19(11):1241-1245.
[10]张丽娅,李德清.变权决策中确定状态变权向量的理想点法[J].数学的实践与认识,2009,39(6):93-97.
[11]Saaty T L.The analytic network process:Decision making with dependence and feedback[M].Pittsburgh: RWS Publications,2004.
[12]Charnes A,Cooper WW,Rhodes E.Measuring the efficiency of decision making units[J].European Journal of Operational Research,1978,2(6):429-444.
[13]Saaty T L.The analytic hierarchy process:Planning,priority setting,resource allocation[M].New York:McGraw Hill,1980.
[14]孙莹,鲍新中.一种基于方差最大化的组合赋权评价方法及其应用[J].中国管理科学,2011,19(6):141-148.
[15]Feng Chengmin,Wu Peiju,Chia K C.A hybrid fuzzy integral decision-making model for locating manufacturing centers in China[J].European Journal of Operational Research,2010,200(1):63-73.
[16]Wu Weiwen.Choosing knowledge management strategies by using a combined ANP and DEMATEL approach[J].Expert Systems with Applications,2008,35(3):828-835.
[17]Green R H,Doyle J R,Cook W D.Preference voting and project ranking using DEA and cross-evaluation[J].European Journal of Operational Research.1996,90(3):461-472.
[18]Dyson R G,Thanssoulis E.Reducing the weight flexibility in data envelopment analysis[J].Journal of the Operational Research Society,1988,39:563-576.
[19]Wong Y H,Beasley J E.Restricting weight flexibility in data envelopment analysis[J].Journal of the Operational Research Society,1990,41(6):829-835.
[20]Wang Yingming,Chin K S.A neutral DEA model for cross-efficiency evaluation and its extension[J].Expert Systems with Applications.2010,37(5):3666-3675.
[21]寇纲,娄春伟,彭怡,等.基于时序多目标方法的主权信用违约风险研究[J].管理科学学报,2012,15(4):81-87.
[22]Wang Yingming,Luo Ying.On rank reversal in decision analysis[J].Mathematical and Computer Modelling,2009,49(5):1221-1229.
Model and Method of Multiple Attribute Decision Making with Relative Variable Weights
LI Chun-hao1,LI Meng-jiao1,MA Hui-xin1,DU Yuan-wei2,LI Jin-jin1
(1.School of Management,Jilin University,Changchun 130022,China;2.Faculty of Management and Economics,Kunming University of Science and Technology,Kunming,690093,China)
Both the multiple factor decision-making method based on variable weights(MFDMM-VW)and the Choquet integral model(CIM)for multiple attribute decision-making(MADM)cannot reflect reasonably the decision-maker's point-dependence preference in MADM.To overcome the mentioned shortcom-ing,a new MADM approach to evaluation and decision making,i.e.,the MADM model with relative variable weights(MADMM-RVW),and its corresponding method are presented based on the swing-weighting,the analytic network process,and the relative evaluation thought embodied in data envelopment analysis.Compared with the MFDMM-VW,the MADMM-RVW is able to reflect directly the decision-maker' s point-dependence preference structure,and thus overcome the arbitrariness of the MFDMM-VW in reflecting the decision-maker's point-dependence preference,resulted from decision analysts when the MFDMM-VW is applied.Compared with the CIM,the MADMM-RVW can not only reflect the decisionmaker's point-dependence preference but also avoid more efficiently the CIM's large-scale estimation problem of decision parameters in many MADM cases.Applied in a case study,the MADMM-RVW is showed to give decision conclusions well consistent with objective existence and the decision-maker's qualitative opinions on preference dependence,and thus be capable of better reflecting the decision-maker's specific preference behaviors.
MADM;decision making with variable weights;preference dependence;swing weighting;analytic network process;data envelopment analysis
C934;N94
:A
1003-207(2014)05-0104-11
2012-08-01;
2013-04-14
国家自然科学基金资助项目(71371083,71261011,70971054);教育部新世纪优秀人才支持计划(NCET -09-0419);教育部人文社会科学研究规划基金(09YJA630047);吉林大学杰出青年基金(2010GL);教育部人文社会科学研究青年基金(12YJC630090)
李春好(1967-),男(汉族),辽宁盖州人,吉林大学管理学院,教授,博士生导师,博士/出站博士后(日本京都大学),研究方向:复杂系统管理决策.

