基于BP神经网络的非结构化道路识别

吕艳鹏，潘玉田

（中北大学 机 电工程学院，山西 太原 030051）

1 BP神经网络

BP（Back Propagation）神经网络是1986年由鲁梅尔哈特（美国）和麦克利兰（美国）为主的科研队伍正式提出的，这是一种按误差反向传播算法训练的多层前馈网络，它由误差反向传播和信息正向传播两个过程组成。随着BP神经网络的快速发展，其实际应用案例已经约占神经网络总体案例的80%。作为最具代表性的神经网络模型，BP神经网络的优越性不言而喻，具有一定的自适应与自组织能力。

一般地，BP神经网络由3层结构构成，其结构示意图如图1所示。其中，左边为输入层，即外界与神经网络的输入接口，它由n个元素组成，输入量分别用x1，x2，…，xn来表示，代表网络的各输入特征值；右边为输出层，有l个元素，传递函数的比例系数为K，输出值为y1，y2，…，yl，代表各目标输出值；介于输入层和输出层中间的为隐层，有m个元素，传递函数选用非线性Sig moid函数。

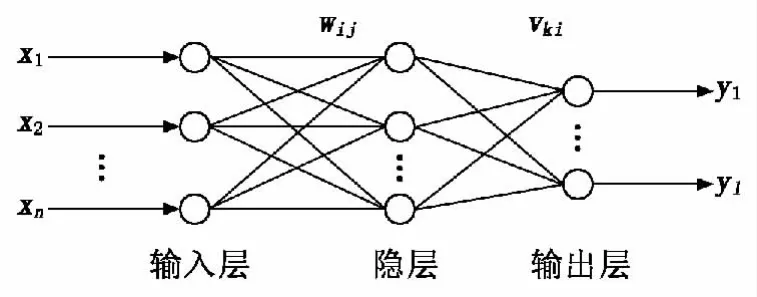
图1 BP神经网络结构示意图

2 BP神经网络算法

神经网络的输入量为x1，x2，…，xn，则隐层的输入量为：

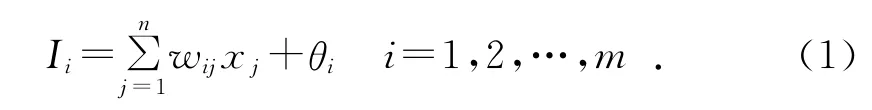
其中：wij为隐层的元素i与输入层的元素j的连接权值；θi为隐层各元素的阀值。

我们取隐层的输入量与输出量之间的传递函数为Sig moid函数，即：

其中：vki为输出层的元素k与隐层的元素i的连接权值；βk为输出层各元素的阀值；yk就是整个神经网络的输出量。

3 隐层节点数的影响

恰当的隐层节点数会显著提高网络的运算效率，比如提升网络训练的识别速度、识别效果和减少识别所需时间。目前业内还没有哪一位研究者提出一套公认的方法来选择适当的隐层节点数，因此，大量的研究者一般是按照实际案例和自身经验，通过试验的方式来选择隐层节点数的多少。

随着隐层节点数的增大，迭代次数也随之增大，网络的识别效果更佳，相应地识别目标所需时间也随之增多，然而这不是一种线性关系，迭代次数、识别效果和识别所需时间的变化幅度会有较大改变。当隐层节点数大于20个，网络的识别效果更加精确，但是识别速度变慢，所用时间也相应的更多。这说明隐层节点数并不是越多越好，需要确定这几个因素的重要性，以此来判断应该优先满足哪个条件。在选择时应根据具体情况和案例的实际要求，主要考虑时间和效果两方面因素，从符合条件的多个隐层节点数中选取一个最合适的。

本文采用线性回归法选取最佳隐层节点数，选择的基本要求是：在识别效果和识别速度同时符合要求的前提下使识别效果最佳，这样可以识别出更加准确的道路。

4 学习率的影响

学习率分为自适应型和固定值型，为简化计算，提高效率，本文选取固定值型。一般地，学习率η与学习速度正相关，但η也不宜过大，否则会引起学习速度振荡或发散。所以，选择一个合适的η对于网络训练的重要性就不言而喻了。有人提出了一个经验公式：

其中：n1为隐层节点数。

学习率和迭代次数之间的关系为：当η＜0.5时，若η增大，则迭代次数随之减少；当η≥0.5时，若η增大，则迭代次数随振荡增加。根据科学家麦克利兰的研究，学习率的取值与网络的输入、输出节点数相关。节点数和学习率负相关，即节点数越大，学习率越小；节点数越小，学习率越大。我们总结出如下的经验公式：

5 BP网络识别算法的应用

首先输入一幅非结构化道路图像，将其平均分成（20×20）像素的小块，然后统计每一个小块的纹理特征值（对比度、熵、相关性、能量和灰度均值），并把这些数据组成的输入向量输入到BP网络中，经过隐层的计算，得到网络的输出结果，对比目标值即可判断该小区域是道路还是非道路区域，从而完成道路的初步判断。

本文设计的BP神经网络算法由3层构成，分别为输入层、输出层和隐层（中间层），如图2所示。输入层由5个元素组成输入向量，分别代表小块的熵、能量、对比度、相关性和灰度均值。输入向量通过处理原始图片可以得到，它将直接跟网络的输入接口连接。为简化网络结构，隐层选用12个元素，选用Sigmoid函数作为隐层的比例函数。由于文章只是为了识别道路与非道路，故输出层只选用1个元素，取0和1来分别代表非道路和道路状态。

随机选取如图3所示的6幅图片，应用Matlab的BP神经网络工具箱进行神经网络的训练。在6幅图片中，选取非道路区域的小块（标为1～6）作为背景训练，目标值取为0；再从6幅图片中选取道路区域的小块（标为7～12）作为目标训练，目标值取为1。提取这些小块中的纹理特征值，见表1。其中，目标值为0的6个小块对应的是非道路区域，目标值为1的6个小块对应的是道路区域，训练算法选用trainl m。

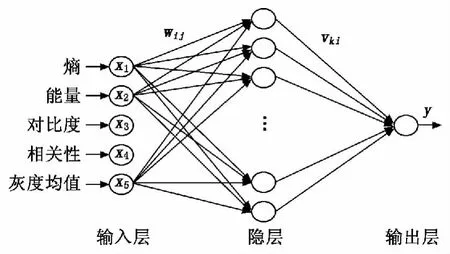
图2 基于纹理特征向量的BP神经网络算法结构示意图

图3 随机抽取的训练图片

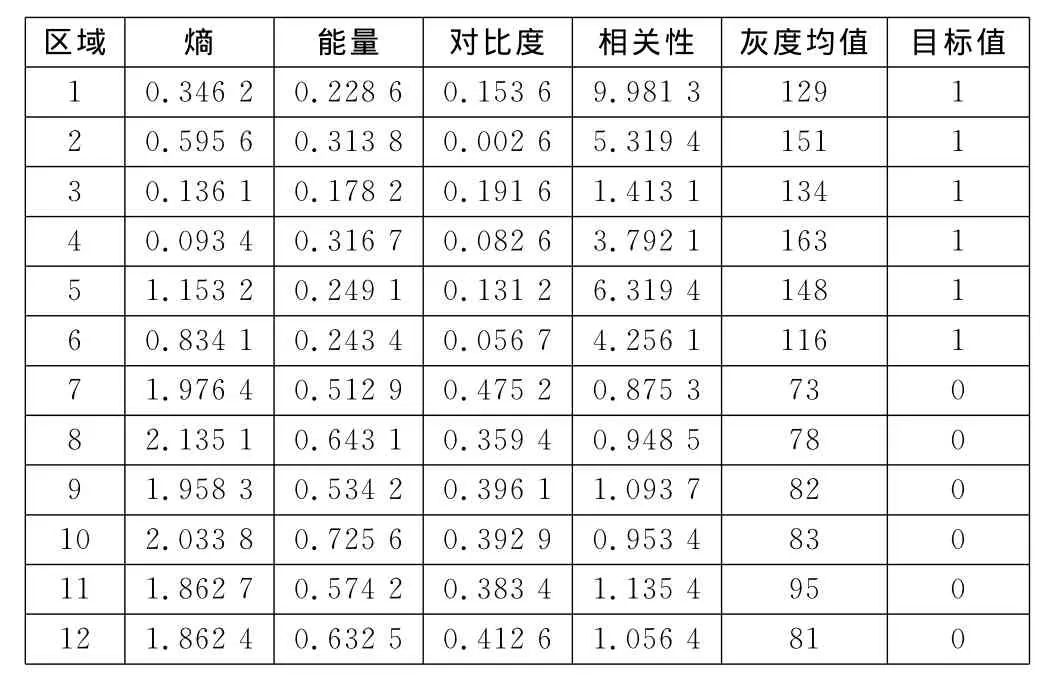
表1 网络训练所用参数及其对应的目标值

根据BP神经网络的特点及道路识别的具体要求，学习率η取1%，训练次数8 000次。经过213次训练，收敛后的误差小于0.001。训练后得到输出层的阀值β＝－0.294 6。

将图片中（20×20）像素的每一个小块的纹理特征值代入到训练后的BP神经网络中，得到道路与非道路区域分割效果，并用回归法得到相应的道路边界，如图4所示。

6 结语

本文基于BP神径网络对非结构化道路图像进行识别。将道路图片中小块的纹理特征代入训练后的BP神径网络，可得到相应的道路边界。

［1］ Leonard J，Kramer M A.Improvement of the back propagation algorithm for training neural net works ［J］.Computers Chem Engng，1990，14（3）：337－341.

［2］ 张乃尧，阎平凡.神经网络与模糊控制［M］.北京：清华大学出版社，1998.

［3］ 田玉敏，梅丽霞.基于综合特征的图像分割［J］.计算机工程与应用，2004（20）：92－94.

［4］ 孙艳霞.纹理分析在遥感图像识别中的应用［D］.乌鲁木齐：新疆大学，2005：22－45.

［5］ 刘子辉.军用无人驾驶车辆非结构化道路识别方法研究［D］.长春：吉林大学，2007：52－68.

［6］ 付忠良.一些新的图像阈值选取方法［J］.计算机应用，2000，20（10）：13－15.