基于前景理论的改进多路径交通分配模型
潘晓锋,左 志,赵胜川
(大连理工大学交通运输学院,辽宁 大连 116024)
1 引 言
在交通分配领域,主要有平衡和非平衡两类模型.非平衡模型由于具有简便、实用等优点,在实践中得到了广泛的应用.其中,多路径分配方法考虑了路网及出行者的随机因素,较之最短路分配更加适用.然而,该方法依旧存在不适用之处:多路径分配的核心是Logit配流模型,Logit模型的基础是“理性人假设”,但是在很多情况下,决策者的选择行为并不表现为完全理性(如著名的阿莱悖论和埃尔斯伯格悖论);同时,Logit模型存在固有的缺陷,在某些特定的情况下不能很好地反映实际情况.
1979年,Kahneman和Tversky将心理学研究成果应用到经济学领域中,分析了决策者的有限理性行为,提出了前景理论[1].1992年,两人在前景理论的基础上,又提出了累积前景理论[2].此后,前景理论成为了研究不确定情况下决策者决策行为的重要理论依据.前景理论认为:①决策者根据参考点判断得失;②决策者面对收益时表现为风险规避,面对损失时表现为风险喜好;③决策者在不确定条件下进行选择时,会忽视所有备选方案共有的部分,使得面对不同情境下相同的问题会出现不同的选择;④前景值V是关于价值v和概率权重w的函数.累积前景理论指出人们在决策时:面对大概率事件,对收益表现为风险规避,对损失表现为风险喜好;而面对小概率事件,对收益表现为风险喜好,对损失表现为风险规避.本文将前景理论与累积前景理论并称为“前景理论”.
前景理论考虑了决策者的心理因素,从收益和损失两方面分析在不确定性条件下决策者的选择行为,已有越来越多的研究将前景理论运用到交通领域之中.郭延永等人提出了一种基于累积前景理论的城市轨道交通线路建设时序决策方法[3].罗清玉等人根据居民出行特点建立了基于前景理论的出行方式选择模型[4],但只是验证了现如今私家车出行越来越多的现象,并没有给出各种出行方式的划分比例.赵凛等人在前景理论的框架下分析了先验信息条件下出行者的学习更新过程,给出了先验信息条件下出行者路径选择的理论模型[5],但是其采用了决定论模型,无法表示大规模出行时出行者的选择概率.张波等人认为路径前景值是分布在出行者总体上的随机变量,它包含一个确定部分和一个随机误差项,从而推导出了基于前景理论的Logit配流模型[6],然而该模型选取了出行时间作为路径选择的唯一影响因素,且由于Logit模型的IIA特性,可能导致类似于“红绿巴士”这样的悖论[7].徐红利等人基于前景理论提出了带有内生参考点的用户均衡模型,并且在该模型基础上分析讨论了拥挤收费[8],但是该均衡模型求解复杂,限制了其自身的应用.
2 基于前景理论的改进多路径分配模型
2.1 基于前景理论的路径选择模型
出行者出行路径选择的影响因素众多,包括出行目的、出行时间和出行距离、费用、准时性等.只用出行时间来度量出行费用显然不能全面体现出行者的选择行为.本文考虑出行时间和出行费用两个最重要的影响因素,应用时间价值定义广义出行费用.广义出行费用的表达式为

式中 C为出行费用;T为出行时间;ρ为私家车时间价值.μ、η分别为出行费用和出行时间的权重,可以表示出行者对待时间和金钱的不同态度.
根据Kahneman和Tversky的研究[2],路径的价值函数可以表示为

式中 xi是某条路径第i种可能结果的损益值,为参考点和广义出行费用之差;xi>0,表示收益,xi<0,表示损失.Uf是决策参考点;λ反映对损失的敏感程度;α、β为待定参数.根据已有研究[9],λ=2.25,α=1.21,β=1.02.
根据Kahneman和Tversky的研究[2],路径的概率权重函数表示为

式中 pi为某路径第i种可能结果的客观概率;γ为待定参数,根据研究[9],γ=0.55,x>0;γ=0.49,x<0.事实上,可以把概率权重函数看作是对客观概率的回归.某条路径前景值的计算表达式为

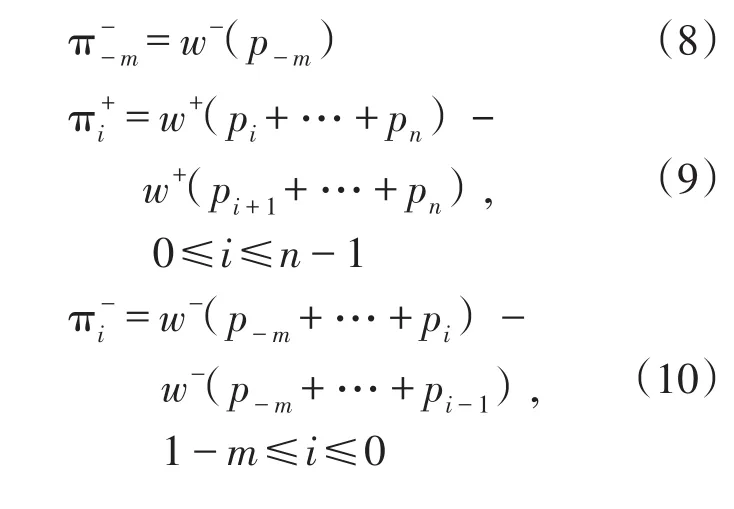
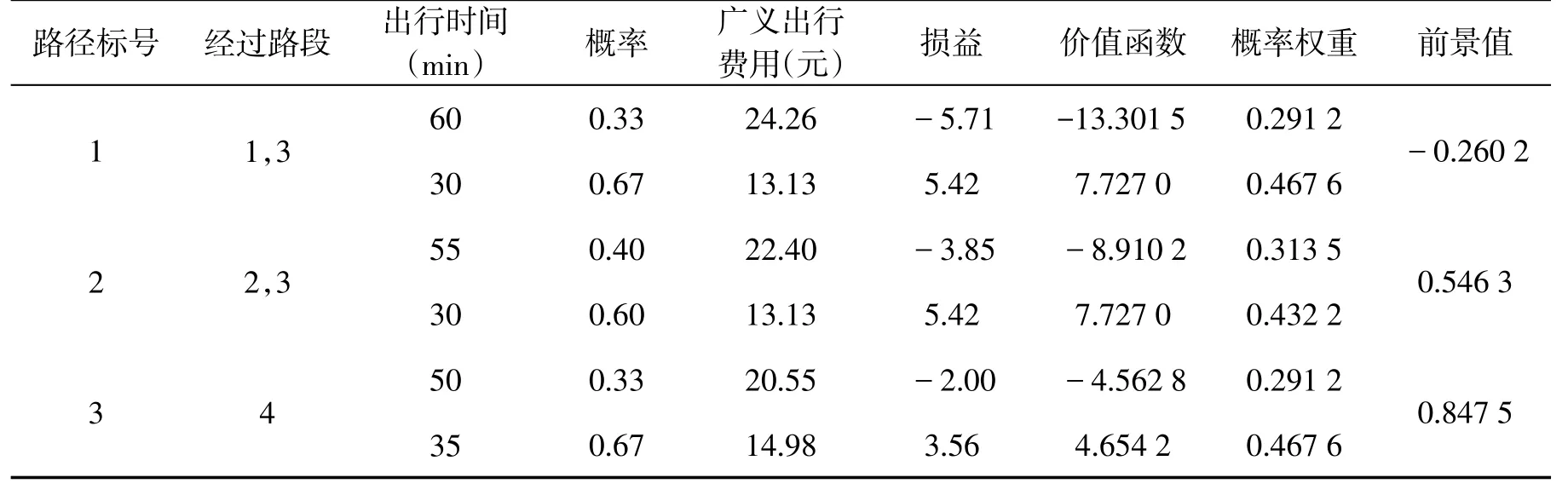
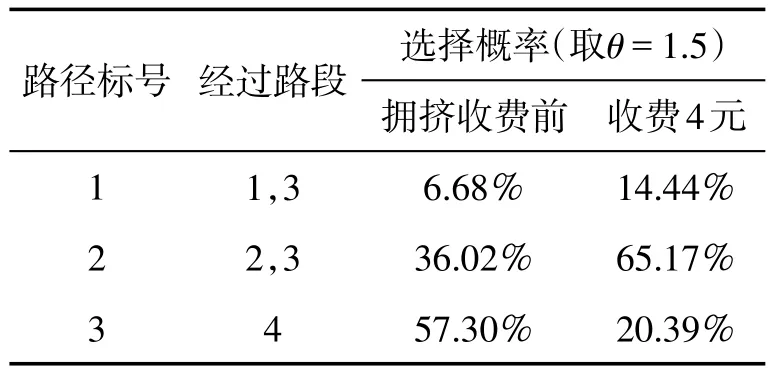
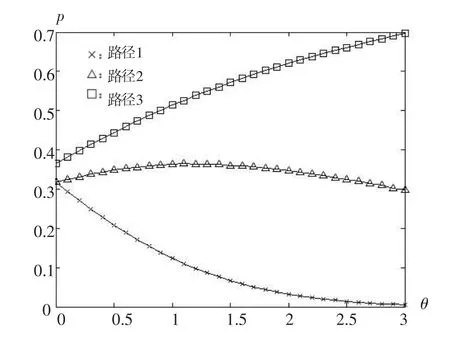
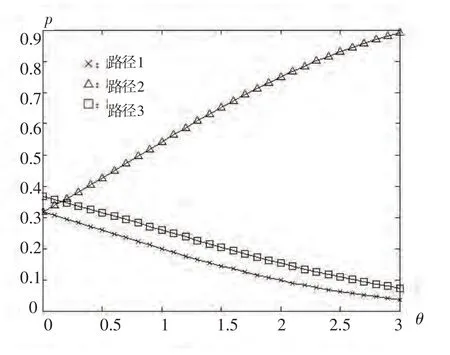
式中 V(f)为某条路径的前景值;x-m 虽然前景理论给出了决策者在面对不确定条件下的决策行为,但是考虑到不同决策者风险态度、认知水平的差异,决策者的决策行为依旧是一个充满随机的过程.前景理论的基本思想是保留期望效用理论的形式,对其内部各因子进行改造,用价值函数和概率权重函数分别替代了期望效用理论中的效用函数和概率[10].因此,可以认为前景值是一种基于“有限理性”的特殊的“效用”.Connors和Sumalee[11]提出了感知前景值的概念,并指出其由固定项和随机项组成,即 式中 PVi是第i条路径的感知前景值;Vi是其固定项,由基于前景理论的路径选择模型计算得到;ξ是随机项,E(ξ)=0;θ表示前景值的度量.通常假设ξ服从参数为(0,1)的二重指数分布,从而推导出Logit模型.但是Logit模型存在两方面的缺陷,一是缺乏对路网结构特性的敏感性,会使过多的流量分配到重合的路径上,二是无法反映感知方差与出行费用之间的依赖关系[12].因此,本文假设ξ服从正态分布,从而得到Probit配流模型.由于Probit模型求解复杂,本文采用蒙特卡罗模拟法求解. 蒙特卡罗模拟法将所求解的问题与某个概率模型联系起来,在计算机上进行随机模拟,以获得问题的近似解.其基本思想是:根据某一概率分布进行大量独立随机试验,取得随机变量的模拟值即样本值的集合,再用数理统计方法求出各种统计量的估计量[13]. 现以数值算例分析改进后的多路径分配模型.采用的路网如图1所示. 在图1中,虚线框表示对该路段实行拥挤收费(假设实施拥挤收费后路径的行程时间不变,即忽略收费排队的影响).设OD对(1,3)之间的需求为1000 PCU/h,出行的燃油费为10元(假设无论选择哪条路径,燃油费均为10元,这当然是不符合实际的,考虑到模型计算的复杂性,故做此假设)根据现有研究[14],私家车的时间价值ρ为27.82元/h,要求在40 min(依据时间价值化为金钱,即18.55元,此即为决策参考点)内达到,可见对出行时间的要求较高,可以令η=0.8,μ=0.2.由图1可知OD对(1,3)之间存在3条可选路径,各路径的出行时间及概率如表1所示. 图1 算例路网Fig.1 Network of the example 表1 各路段的出行时间及概率Table 1 Travel time and probabilities of paths 依据本文之前提出的多路径分配模型,结合算例的具体数据,可以得到实施拥挤收费前后各条路径的前景值.具体如表2、表3所示. 表2 各路径的前景值(拥挤收费前)Table 2 Prospects of paths(before congestion pricing) 表3 各路径的前景值(收费:4元)Table 3 Prospects of paths(charging 4 RMB) 假设感知前景值(PV1,PV2,PV3)服从多维正态分布,各条路径的感知方差均为2,路径1和路径2的相关系数为0.5,故两者的协方差为1.路径3与其余路径不相关.即 由此可推导出Probit模型,应用蒙特卡罗模拟法,随机产生1000000组随机数,通过计算可得实施拥挤收费前后,各条路径的选择概率和其上的流量,如表4及图2所示. 表4 各路径的选择概率Table 4 Choice probabilities of paths 图2 收费前后各路段上的流量(单位:PCU/h)Fig.2 Volumes of links before and after congestion pricing(unit:PCU/h) 现在讨论参数θ的变化对各路段选择概率的影响.图3、图4显示了实施拥挤收费前后,θ从0变化到3时,各路径的选择概率. 图3 拥挤收费前,各路径选择概率随θ值的变化Fig.3 Choice probabilities’change with θ before congestion pricing 图4 收费4元时,各路径选择概率随θ值的变化Fig.4 Choice probabilities’change with θ when charging 4 RMB 表4显示,拥挤收费对出行者的出行选择存在影响.现在讨论不同收费标准对路网流量的影响程度.在θ=1.5时,不同收费标准与各路径的选择概率如图5(收费标准从0元变化至6元)所示. 由表3、表4可知,拥挤收费能够影响出行者的出行路径选择.在实施收费之前,各条路径的前景值分别为-0.2602、0.5463、0.8475,路径 3 的前景值最大;而实施拥挤收费之后,路径3的前景值发生了变化,在收费4元的情况下减少为-0.2727,此时前景值最大的路径为路径2. 图5 不同收费标准下各路径的选择概率(θ=1.5)Fig.5 Choice probabilities under different charging standards(θ=1.5) 参数θ是前景值的度量,反映的是出行者对待可选路径的认知程度.若θ=0,表明出行者对各条路径的认知没有差别,路径的选择只与路网本身的特性有关.由图3、图4可知,当θ=0时,无论是否收费,各条路径的选择概率均在0.3~0.4的较小范围之内.随着θ不断增大,前景值最大的路径开始显示其优势,θ值越大,其优势越明显.当θ趋于无穷大时,此概率论模型就转换为决定论模型.因此,θ在此模型中是一个关键的参数,不同的θ值会得到不同的分配结果,在实际应用中需要经过调查分析得到. 从图5可知,拥挤收费不仅能够引起路网上流量的重新分配,且在不同的收费标准下流量的分配不相同.图5中有两个交点,分别为(1.1850,0.4551)和(4.7730,0.1554).路径1的选择概率始终在0.2以下,可以认为路径1不是主要路径.路径2和路径3的选择概率对路网上的流量分配影响较大.因此,交点(1.1850,0.4551)是一个近似最优点,即收费1.19元时,路径1的选择概率为8.98%,路径2和路径3的选择概率均为45.51%.此时各路段上的流量分别为:X1=90(PCU/h),X2=455(PCU/h),X3=545(PCU/h),X4=455(PCU/h). 多路径交通分配模型由于计算简单、实用等优点而被广为采用.本文基于前景理论和Probit模型,讨论了原始多路径分配模型中的缺点,提出了一个改进模型,并分析了拥挤收费政策对路网流量的影响.下一步的研究可以从以下几个方面出发:①将该模型应用于更加复杂的路网,以分析参数θ的特性,进一步验证模型的适用性;②该模型可以作为平衡模型的基础,讨论基于该模型的平衡问题;③将该模型应用于城市实际路网,以确定合适的收费标准,为制定合理的拥挤收费政策提供依据. [1]Kahneman D,Tversky A. Prospect theory:an analysis of decision under risk[J]. Econometrica:Journal of the Econometric Society,1979:263-291. [2]Tversky A,Kahneman D. Advances in prospect theo⁃ry:cumulative representation of uncertainty[J]. Jour⁃nal of Risk and Uncertainty,1992,5(4):297-323. [3]郭延永,刘攀,吴瑶.基于累计前景理论的城市轨道交通建设时序[J].交通运输系统工程与信息,2013,13(4):29-35.[GUO Y Y,LIU P,WU Y. Construc⁃tion sequence of urban rail transit system based on cu⁃mulative prospect theory[J].Journal of Transportation System Engineering and Information Technology,2013,13(4):29-35.] [4]罗清玉,吴文静,贾洪飞,等.基于前景理论的居民出行方式选择分析[J].交通信息与安全,2012,30(2):37-40.[LUO Q Y,WU W J,JIA H F,et al.Analysis of residents travel mode choice based on pros⁃pect theory[J].Journal of Transport Information and Safety,2012,30(2):37-40.] [5]赵凛,张星臣.基于“前景理论”的先验信息下出行者路径选择模型[J].交通运输系统工程与信息,2006,6(2):42-46.[ZHAO L,ZHANG X C. A pros⁃pect theory based route choice model of traveler with pri⁃or information[J]. Journal of Transportation System En⁃gineering and Information Technology,2012,6(2):42-46.] [6]张波,隽志才,林徐勋.基于累积前景理论的随机用户均衡交通分配模型[J].西南交通大学学报,2011,46(5):868-874.[ZHANG B,JUAN Z C,LIN X X. Stochastic user equilibrium model based on cu⁃mulative prospect theory[J]. Journal of Southwest Jiao⁃tong University,2011,46(5):868-874.] [7]关宏志.非集计模型:交通行为分析的工具[M].北京:人民交通出版社,2004.[GUAN H Z.Disaggre⁃gate model:a tool of traffic behavior analysis[M]. Bei⁃jing:China Communications Press,2004] [8]Xu H,Lou Y,Yin Y,et al. A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing[J]. Transpor⁃tation Research Part B:Methodological,2011,45(2):311-328. [9]曾建敏.实验检验累积前景理论[J].暨南大学学报(自然科学版),2007,28(1):44-47+65.[ZENG J M.An experimental test on cumulative prospect theory[J].Journal of Jinan University(Natural Science).2007,28(1):44-47+65.] [10]庄锦英.决策心理学[M].上海:上海教育出版社,2006.[ZHUANG J Y. The psychology of decisionmaking[M]. Shanghai:Shanghai Educational Publish⁃ing House,2006.] [11]Connors R D,Sumalee A. A network equilibrium mod⁃el with travellers’perception of stochastic travel times[J].Transportation Research Part B:Methodological,2009,43(6):614-624. [12]Sheffi Y. Urban transportation networks:equilibrium analysis with mathematical programming methods[M].Prentice-Hall,INC,Englewood Cliffs,New Jersey,1985. [13]王玮,陆建.道路交通工程系统分析方法(第二版)[M].北京:人民交通出版社,2011.[WANG W,LU J. System analysis methods for highway and traffic en⁃gineering(the second edition)[M]. Beijing:China Communication Press,2011.] [14] 张羽祥.私家车通勤出行时间价值研究[D].大连理工大学,2008.[ZHANG Y X. Value of drivers’commuting travel time[D]. Dalian University of Tech⁃nology,2008.]2.2 改进的多路径分配模型
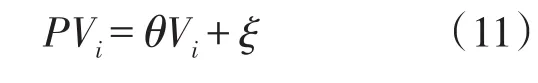
3 算例


3.1 选择概率及流量的计算



3.2 参数值θ的讨论
3.3 收费标准的讨论
3.4 结果分析

4 研究结论

