基于频响函数曲率的结构损伤检测
夏提古力·肖开提,阿肯江·托呼提,朱新圆
(新疆大学 建筑工程学院,乌鲁木齐 830047)
在规定的服役寿命期间内,结构由于受到冲击、地震、风荷载、腐蚀等作用,材料内部结构会发生变化,由此必然会产生各种各样的损伤。如今,土木工程结构的安全性问题日益引起人们的关注,损伤无时无刻不威胁着人民的生命财产安全。因此,及时发现损伤并对其进行修复非常重要。
从损伤结构可以得到结构的主要特征指标,如结构位移模态振型、固有频率、位移(速度、加速度)频率响应函数(frequency response function,FRF)、曲率模态振型、应变模态振型、应变频率响应函数等。这些特征参数均可以与未损伤结构的系统质量和刚度相关联,可以通过比较未损伤结构与损伤结构的振动信息确定损伤的位置和程度[1]。许多学者提出了基于振动理论的损伤检测方法,如基于频率变化的损伤识别方法、基于振型变化的损伤识别方法、基于刚度或柔度变化的损伤识别方法、基于能量变化的损伤识别方法、基于应变模态的损伤识别方法、基于曲率模态的损伤识别方法等[2-4]。在文献[5]中 Maia以数值计算的方法对两种方法进行比较,对比结果表明频响函数曲率对损伤位置更加敏感。频响函数曲率不需要数学模型,可用于在线损伤监测,测量简单且包含更丰富的信息,是一个很好的敏感参数。
1 理论依据
多自由度阻尼系统的强迫振动方程为:

对式(1)两边进行拉氏变换得

式中:Y(s)、F(s)分别为y、f的拉氏变换。
由式(2)可得

其中,
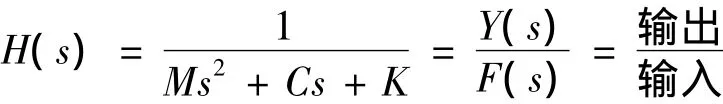
令S=jw,即将拉氏变换变成傅里叶变换,则有频响函数
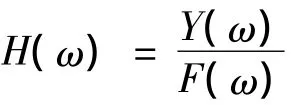
在进行结构损伤识别时,以频响函数的曲率作为损伤识别参数,基于损伤结构和未损结构的曲率变化来识别。这里的曲率由中心差分的方法得到,即
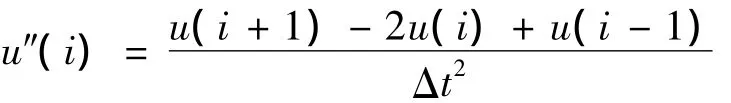
这个变化通过曲率差或曲率比表示。
Pandey[6]用损伤前后的曲率差来判定结构的损伤位置。损伤前后曲率计算如下:
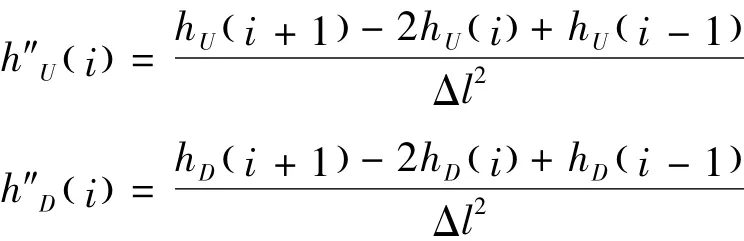
获得了结构损伤前后的频响函数曲率h″U和h″D以后,频响函数曲率差可以表示为
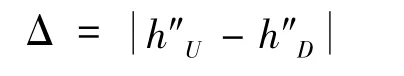
式中,Δ可以用作损伤诊断的指标。则曲率比α为
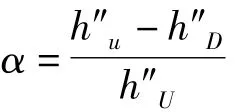
2 算例分析
本文利用有限元数值模拟的方法分别对相同的简支梁结构,如图1所示,在不同的损伤条件下进行了数值试验。本算例中,梁分为十个单元,结构损伤表现为降低损伤单元的刚度,质量保持不变。损伤导致的刚度的降低用弹性模量的减少来模拟。梁尺寸为2 000 mm×100 mm×200 mm,在无损情况下材料特性为:E=2.0×105MPa,ν=0.3,ρ=7.8×103kg·m-3。
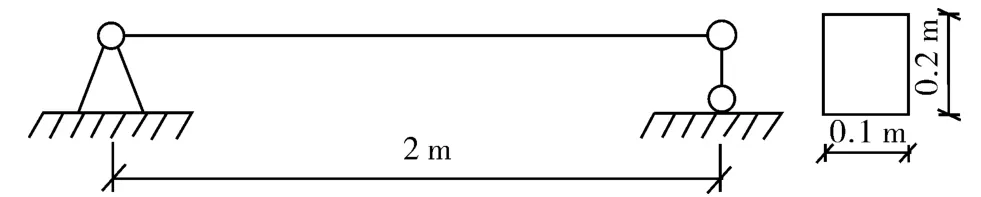
图1 简支梁模型
根据损伤位置及损伤程度的不同,考虑了三种损伤工况,如表1所示。
根据上述三种工况的有限元分析结果,分别算出频响函数曲率、频响函数曲率差、频响函数曲率比进行损伤诊断。图2分别为结构单处(5号单元)损伤时的三种指标诊断结果。频响函数曲率(见图2(a))在结构损伤处有突变,但因为是一条二次曲线,损伤又刚好发生在曲线峰值处,故在损伤程度较小时突变不明显。而频响函数曲率差(见图2(b))及曲率比(见图2(c))除了在损伤位置处有突变外,其余位置基本是水平的,很容易识别出损伤位置。故这两种指标对损伤位置更敏感,且随着损伤程度的增大,指标变化越明显。这表明,三种指标变化率与结构损伤程度成正比。

表1 结构损伤工况
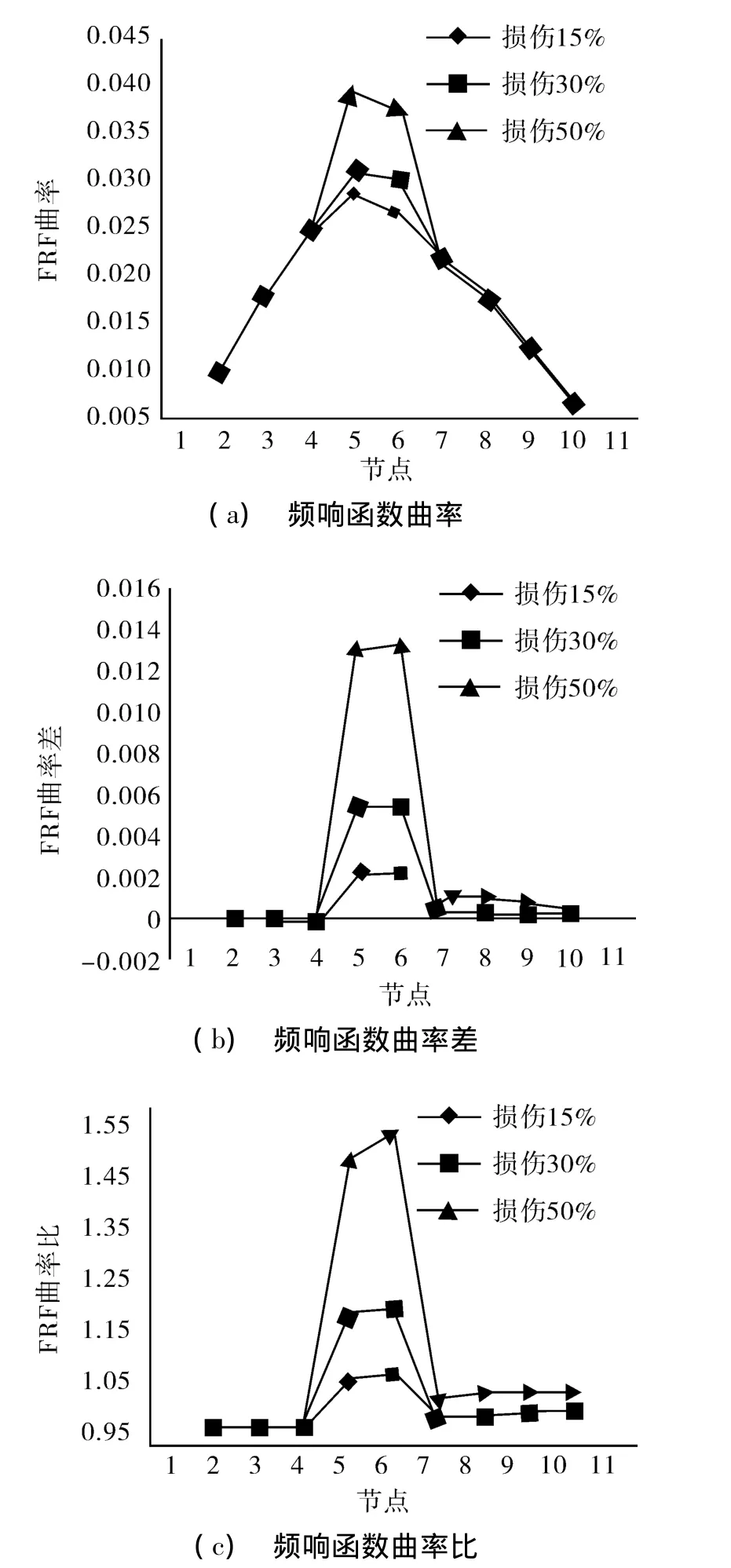
图2 工况2的三种指标诊断结果

图3 工况3三种指标诊断结果
图3结果表明,在结构多处损伤时,上述三种指标也可以正确反映出损伤位置,且随着损伤程度的增大指标变化程度也增大。在多处损伤工况时,频响函数曲率差(图b)随着损伤程度的增大而减小,成反比,而且跟频响函数曲率一样整体呈曲线。与之相比,频响函数曲率比(图c)除损伤位置有突变外,其余位置基本水平,很容易识别出损伤位置。这表明,结构发生多处损伤时,频响函数曲率比对损伤更敏感。
结合上述两种分析结果,对比发现,这三种指标中,频响函数曲率比的损伤诊断效果更好,即使是在损伤程度较小时也能精确判别出损伤位置。
3 结束语
从简支梁的算例结果分析可以看出:
1)频响函数的曲率、曲率差及曲率比这三项指标能够准确地反映出损伤点的位置及损伤的大小,并且计算方便,是很好的敏感参数。
2)在结构中有单处损伤时曲率差及曲率比较曲率对损伤更敏感些,但是当结构多处损伤时,频响函数曲率比对位置的敏感程度更为突出。
[1]王术新,姜哲.基于结构振动损伤识别技术的研究现状及进展[J].振动与冲击,2004,23(4):99-102.
[2]郭惠勇,罗乐,李正良.基于刚度指标和频率的结构损伤定性定量识别[J].西南交通大学学报,2008,43(4):447-452.
[3]张开银,孙峙华.桥梁结构损伤识别的曲率模态技术[J].武汉理工大学学报,2004,28(6):855-858.
[4]郑明刚,刘天雄,陈兆能.基于频响函数的结构损伤检测[J].机械科学与技术,2001,20(3):458.
[5]Maia N M M,Silva J M M.Damage detection using the frequency response function curvature method[J].Journal of Sound and Vibration 1999,226(5):1029-1042.
[6]Pandey A K,Biswas M.Damage detection in structures using changes in flexibility[J].Journal of Sound and Vibration,1994,169(1):3-17

