经典恒温法和多元线性模型预测头孢甲肟在输液中的热稳定性*

王建欣,张辰辰,杨继章,谷体心

(1.河北医科大学第一医院药剂科,石家庄 050031；2.河北医科大学药学院,石家庄 050017)

·用药指南·

经典恒温法和多元线性模型预测头孢甲肟在输液中的热稳定性*

王建欣1,张辰辰2,杨继章1,谷体心1

(1.河北医科大学第一医院药剂科,石家庄 050031；2.河北医科大学药学院,石家庄 050017)

目的 研究注射用盐酸头孢甲肟在大输液中的热降解动力学过程,预测其热稳定性。方法采用高效液相色谱法测定头孢甲肟含量,用经典恒温法和多元线性模型两种方法计算头孢甲肟在大输液中的有效期。结果头孢甲肟在两种大输液中的热降解动力学过程符合一级动力学特征,用经典恒温法和多元线性模型预测头孢甲肟在0.9%氯化钠注射液中的有效期分别为2.20和1.52 d;在5%葡萄糖注射液中的有效期分别为2.09和1.53 d。结论头孢甲肟在0.9%氯化钠注射液和5%葡萄糖注射液中的热稳定性差,两种方法预测的有效期基本一致。

头孢甲肟;热降解动力学;经典恒温法;多元线性模型;色谱法,高效液相

头孢甲肟为半合成第3代头孢菌素,具有抗菌谱广、杀菌力和耐酶性强、不良反应少等特点[1],近年已在临床广泛应用。从临床应用角度探索注射用盐酸头孢甲肟在2种常用大输液中的热降解动力学规律,预测其稳定性及有效期,有助于确定其适宜的临床使用条件,减少药物在使用过程中降解、变质。笔者采用经典恒温法和多元线性模型计算了头孢甲肟在0.9%氯化钠注射液和5%葡萄糖注射液中的有效期,旨为临床安全、有效用药提供参考。

1 仪器与试药

1.1 仪器 LC-10AT型高效液相色谱仪(日本岛津公司),包括ClASS-VP工作站,SPD-10Avp检测器,SCL-10Avp控制器,CTO-10Asvp柱温箱；BS210S型电子分析天平(北京赛多利斯天平有限公司)。

1.2 试药 头孢甲肟对照品(中国食品药品检定研究院,含量:94.6%)；注射用盐酸头孢甲肟(浙江尖峰药业有限公司,规格:1.0 g,批号:120103)；0.9%氯化钠注射液(石家庄四药有限公司,批号:1205241401)；5%葡萄糖注射液(石家庄四药有限公司,批号: 1205231401)；乙腈为色谱纯。

2 方法与结果

2.1 色谱条件 色谱柱:DiamonsilTMC18(250 mm×4.6 mm,5μm)；流动相:水-乙腈-冰醋酸(50∶10∶1)；检测波长:254 nm；进样量:20μL。

2.2 标准溶液的配制 精密称取头孢甲肟对照品适量,加0.1 mol·L-1、pH6.8的磷酸盐缓冲液2 mL溶解,用流动相稀释制成浓度为1 152.0,864.0,576.0, 402.0,288.0,144.0 mg·L-1头孢甲肟对照品溶液。

2.3 供试液的配制 供试液A:模拟临床常用浓度,取注射用盐酸头孢甲肟(规格:1.0 g)1瓶,注入0.9%氯化钠注射液10 mL,振荡2 min,使头孢甲肟完全溶解后,再用0.9%氯化钠注射液稀释至100 mL。

供试液B:模拟临床常用浓度,取注射用盐酸头孢甲肟(规格:1.0 g)1瓶,注入5%葡萄糖注射液10 mL,振荡2 min,使头孢甲肟完全溶解后,再用5%葡萄糖注射液稀释至100 m L。

2.4 专属性实验 取浓度为288.0 mg·L-1头孢甲肟对照品溶液,按“2.1”项进样测定。另配制供试液A和供试液B适量,置90℃水浴中做加速实验,分别于0和20 min精密量取上述溶液适量,加流动相稀释后同法测定。结果,加速实验后出现的降解产物未干扰头孢甲肟色谱峰,色谱图见图1。

2.5 标准曲线的制备 将“2.2”项配制的一系列标准溶液按“2.1”项进样测定,以峰面积(A)对相应浓度(C)进行线性回归,得回归方程A=31 722C+30 203 (r=0.999 5)。结果表明,在144.0～1 152.0 mg·L-1范围内,头孢甲肟峰面积与浓度呈良好的线性关系。

2.6 精密度实验 浓度分别为864.0,402.0, 144.0 mg·L-1头孢甲肟对照品溶液,按“2.1”项下进样测定。每个浓度在1 d内平行操作5次,计算日内精密度；每天平行操作1次,连续5 d,计算日间精密度。结果显示,日内精密度的RSD=0.92%(n=5)；日间精密度的RSD=1.29%(n=5)。

2.7 加样回收率实验 在已知含量供试液A和供试液B中,分别加入浓度为864.0,402.0,144.0 mg·L-1的头孢甲肟对照品溶液,每个浓度各3份,按“2.1”项测定平均回收率和RSD,分别为:在供试液A中平均回收率99.9%,RSD=0.73%(n=9)；在供试液B中平均回收率99.7%,RSD=0.79%(n=9)。

2.8 经典恒温实验 将供试液A、B分别置于60,70, 80,90℃恒温水浴中加速反应。即时取样作为0 min浓度,恒温加热,于不同时间点取样,置于冷水浴中使之迅速冷却以终止反应,按“2.1”项进样测定,记录峰面积,代入回归方程计算头孢甲肟的含量。结果见表1。

2.9 数据处理

2.9.1 经典恒温法 对供试液A、B的含量测定结果分别运用化学动力学原理进行计算[2-3]。即以供试液中头孢甲肟百分含量的对数(lgC)对时间t进行回归,判断反应级数。一级反应lgC=-(K/2.303)t+lgC0。从斜率可求出各个温度下药物降解速率常数K,以lgK对1/T进行回归,得Arrhenius方程,由此推算出25℃时的反应降解速率常数(K25℃),及头孢甲肟下降10%时所需要的时间即有效期(t0.9=0.105 4/K)。结果,各温度下的百分含量的对数lgC对时间t进行回归,相关系数r的绝对值均＞0.99,说明头孢甲肟在0.9%氯化钠注射液和5%葡萄糖注射液中的降解均遵循一级动力学反应。按各降解的线性方程推算出各温度下的降解速率常数,结果见表2。将表中lgK对1/T经回归处理后得Arrhenius方程:在供试液A中为lgK= -4 874.3328×(1/T)+13.646；在供试液B中为lgK= -4 861.8×(1/T)+11.850。由方程求得,供试液A中:K25℃=0.001 996 h-1,t0.9=0.105 4/K25℃=52.807 0 h(2.20 d)；供试液B中:K25℃=0.002 103 h-1,t0.9= 0.105 4/K25℃=50.116 7 h(2.09 d)。

A.对照品;B.供试液A配制后0 min;C.供试液A 90℃加热20 min后;D.供试液B配制后0min;E.供试液B 90℃加热20 min后;1.头孢甲肟图1 5种溶液的高效液相色谱图A.reference substance of cefmenoxime；B.test solution A at 0 minutes after preparation；C.test solution A at 20 minutes after preparation at 90℃；D.test solution B at 0 minutes after preparation；E.test solution B at 20 minutes after preparation at 90℃；1. cefmenoximeFig.1 HPLC ch romatogram of five kinds of solutions

表1 供试液A、B在不同温度及加速时间下头孢甲肟的含量Tab.1 Content of cefm enoxime in the test solution A and B at d ifferent acceleration time and experimental tem perature mg·L-1,n=5,

温度与时间头孢甲肟含量供试液A供试液B 温度与时间头孢甲肟含量供试液A供试液B 60℃80℃0 min 1 010.2±0.6 986.4±0.4 0 min 1 014.7±0.7993.1±0.8 60 min 870.5±0.8 812.0±0.6 30min 633.5±0.6634.5±0.8 120 min 773.0±0.4 745.8±0.7 60min 435.0±0.6442.6±0.9 180 min 679.5±1.0 692.6±0.6 90 min 313.0±0.5323.7±1.0 240 min 617.5±1.2 597.2±0.9 105 min 261.7±0.8 298.2±1.0 360 min 504.7±1.0 484.2±0.9 120 min 228.4±1.2 229.3±1.2 480 min 415.5±1.5 398.2±1.5 150min 164.3±1.5 173.2±1.1 70℃90℃0 min 1 045.8±0.5 1 020.5±0.2 0 min 997.7±0.31 005.2±0.4 30 min 875.5±0.8 845.7±0.5 10 min 822.3±0.5758.6±0.8 60 min 748.2±0.6 690.8±0.5 20 min 559.2±0.8517.3±0.9 120 min 563.4±0.9 510.7±0.6 30min 421.3±0.9379.7±0.7 170 min 462.3±0.7 407.9±0.8 40min 320.7±1.0282.2±0.8 220 min 386.7±1.2 327.4±1.2 50 min 239.9±1.0216.0±0.9 270 min 331.5±1.1 268.7±1.0 60 min 192.3±1.3169.8±1.2

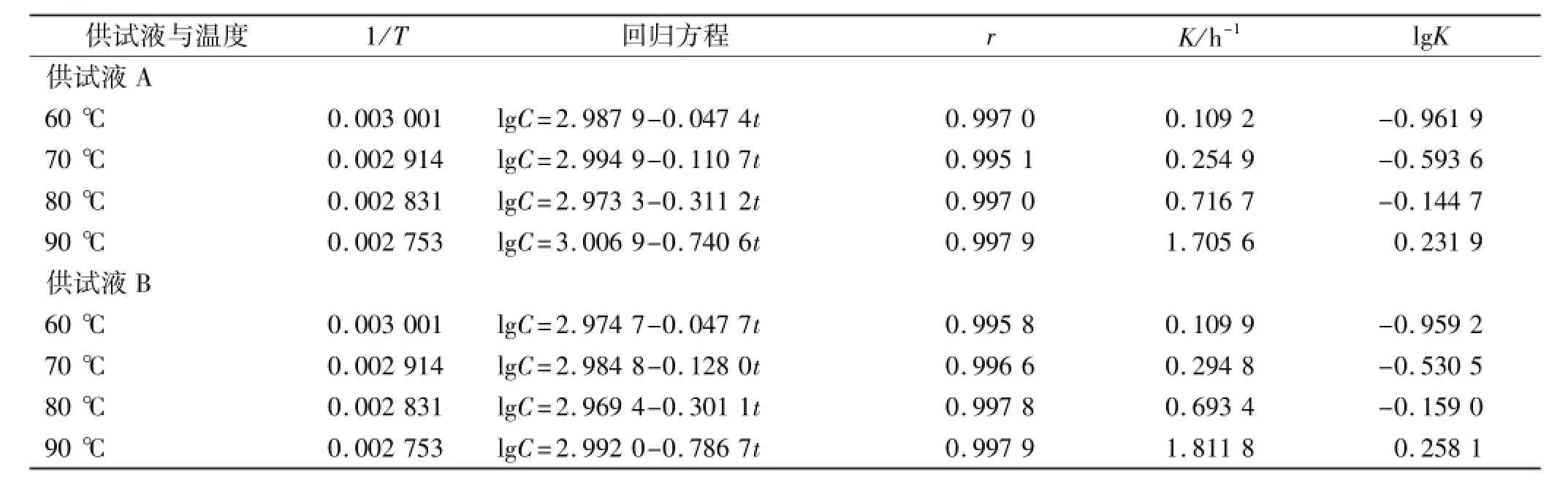
表2 不同温度下头孢甲肟在供试液A和供试液B中的降解反应方程及速率常数Tab.2 Equation and constant of reaction of cefmenoxime in the test solution A and solution B at different experimental temperature

2.9.2 多元线性模型 根据药物降解反应恒温动力学的基本公式f(C0)-f(C)=k(T)t和Arrhenius公式k (T)=Ae-E/(RT)得多元线性模型的基本公式lnt=ln[f (C0)-f(C)]+E/(RT)-lnA(式中t为取样时间,C0为起始药物浓度,C为t时间药物浓度,f(C)为浓度函数,E为活化能,R为摩尔气体常数,T为反应温度,A为频率因子)。一级动力学过程中f(C)=lnC,对于某一药物来说,E和A为常数,即在一定的温度下,E/ (RT)-lnA为一定值,也就是ln(t)-ln[f(C0)-f(C)]为一定值。令Y=ln(t)-ln[f(C0)-f(C)],则公式可简化为Y=E/R×1/T-lnA。以Y对1/T进行线性回归,得回归方程。以C=0.9C0代入,由此方程推算出药物在25℃(298.2K)时浓度下降至初始浓度10%的时间。在表1,2中各温度条件下,任选2个数据(加星号)进行相应的数学处理,结果见表3。

以Y对1/T进行线性回归,得回归方程供试液A中:Y=10 731×1/T-30.14(r=0.996)；供试液B中:Y=10 767×1/T-30.25(r=0.995)。以C=0.9C0代入,即求得药物在25℃时浓度下降至初始浓度10%的时间分别为:供试液A中为36.4221 h(1.52 d),供试液B中为36.814 8 h(1.53 d)。

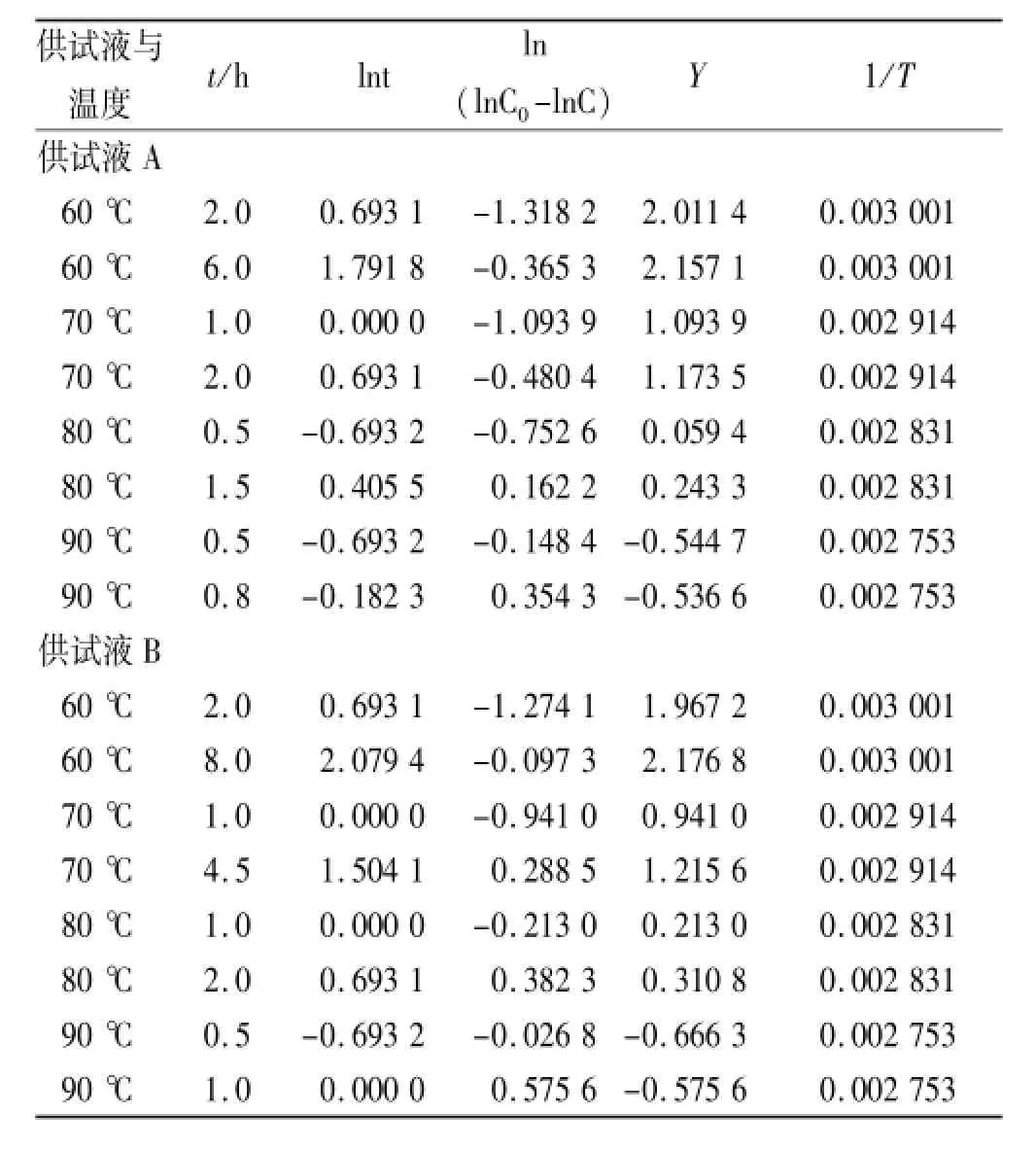
表3 头孢甲肟在供试液A和供试液B中多元线性模型的计算结果Tab.3 Com putation of multip le linear m odel of cefmenoxime in the test solution A or soluton B

3 讨论

随着医院药学的发展,静脉药物的集中配制将逐步取代在护理站的配制,对药物配制后的放置时间和储存条件有了更高的要求。头孢菌素类抗菌药物由于具有不稳定的β-内酰胺环,易受亲核、亲电试剂的攻击,与酸、碱及某些金属离子作用时易发生水解和分子重排[4]。此外,头孢菌素类抗菌药物与输液配制后受温度、光线及pH的影响增大,易导致其疗效降低或变态反应增加。但对头孢菌素类抗菌药物与输液配置后的具体有效期尚未见报道。

笔者应用经典恒温法和多元线性模型对头孢甲肟在0.9%氯化钠注射液和5%葡萄糖注射液中的有效期进行了初步预测。相对于经典恒温加速法,多元线性模型取样点数量较少(总共在不同温度下有5个以上数据即可),计算时回归次数较少,因此更为经济、简单；但其缺点是,该方法必须在已知药物降解反应级数的前提下进行。本研究中2种方法预测得到的结果基本一致。

头孢甲肟对照品直接加入到流动相中不能较好的溶解,故本文中参照文献[5]做法:先用少量pH6.8的磷酸缓冲液溶解后,再用流动相稀释,头孢甲肟溶解较好。此外,为加快注射用盐酸头孢甲肟溶解,提高输液澄清度,建议配制静脉输液时,先在头孢甲肟西林瓶中注入10～20 mL注射用水,振荡2 min,溶解后再用0.9%氯化钠注射液或5%葡萄糖注射液稀释使用[1]。若未待头孢甲肟完全溶解即加入输液中,易形成不溶微粒,反而使其更难溶解。笔者采用的方法是:先从输液袋中抽出0.9%氯化钠注射液或5%葡萄糖注射液10 mL注入头孢甲肟西林瓶中,振荡溶解后再加入相应的输液袋中稀释,这样既能接近临床实际做法,又可方便计算头孢甲肟的浓度。

头孢甲肟与0.9%氯化钠注射液和5%葡萄糖注射液配制后热稳定性较差,临床使用时应避免室温过高,应临用现配,且尽快用完。笔者仅考察了头孢甲肟与输液配制后的热稳定性,其对光线和pH的稳定性有待于进一步研究。

[1] 马瑛,董卫华,董亚琳,等.注射用盐酸头孢甲肟静脉配置方案和稳定性考察[J].中国医院药学杂志,2010,30(7): 606-608.

[2] 熊建华,孙丽蓉,王淑君,等.注射用阿洛西林钠在5%木糖醇注射液中的稳定性考察[J].中国现代应用药学, 2009,26(3):248-251.

[3] 汝玲,韩方璇,黄春新.经典恒温加速法和多元线性模型预测头孢米诺钠水溶液的稳定性[J].中国药房,2006,17 (19):1500-1502.

[4] 叶红,潘玲丽.头孢类抗菌素在输液中的稳定性[J].中国药师,2006,9(11):1069-1071.

[5] 李群力,刘家健,黄金龙,等.注射用盐酸头孢甲肟含量测定及有关物质检查方法的研究[J].中国抗生素杂志, 2006,31(12):755-757.

DOI 10.3870/yydb.2014.05.036

Detecting Thermal Stability of Cefmenoxime Hydrochloride in Infusion Solutions by Classical Isothermal Kinetic Method and Multivariate Linear Model

WANG Jian-xin1,ZHANG Chen-chen2,YANG Ji-zhang1,GU Ti-xin1
(1.Department of Pharmacy,the First Hospital of Hebei Medical University,Shijiazhuang 050031,China;2.School of Pharmacy,Hebei Medical University,Shijiazhuang 050017,China)

ObjectiveTo investigate thermal degradation kinetic characteristics of cefmenoxime hydrochloride in infusion solutions,and predict its thermal stability.MethodsThe HPLC was applied to determ ine the contents of cefmenoxime hydrochloride.Classical isothermal kinetic method and multivariate linear model were used to predict the expiration date of the injection.ResultsItwas found that the thermal degradation kinetics of cefmenoxime hydrochloride in two infusion solutions corresponded with the first-order kinetics.The expiration dates of cefmenoxime hydrochloride in 0.9%sodium chloride injection calculated by two differentmethodswere 2.20 days and 1.52 days,and in 5%glucose injection were 2.09 days and 1.53 days, respectively.ConclusionThe thermal stability of cefmenoxime hydrochloride in infusion solutions is poor and its expiration dates are the same calculated by two differentmethods.

Cefmenoxime;Thermal degradation kinetic;Classical isothermal kinetic method;Multivariate linear model;Chromatography,high performance liquid

R978.1;R927.2

A

1004-0781(2014)05-0668-04

2013-05-20

2013-08-07

*河北省医学科学研究重点课题(20120276)

王建欣(1982-),女,河北藁城人,主管药师,硕士,研究方向:药物的降解动力学及配伍稳定性。电话:0311-85917354,E-mail:wjx76242756@126.com。

杨继章(1957-),男,河北邢台人,主任药师,硕士生导师,研究方向:药物稳定性。电话:0311-85917352,E-mail:yjzh1957@163.com。