广义EuIer常数
刘云 李晓兰
(玉溪师范学院 理学院,云南 玉溪 653100)
[数学]
广义EuIer常数
刘云 李晓兰
(玉溪师范学院 理学院,云南 玉溪 653100)
数学常数;Euler常数;广义Euler常数
定义了广义Euler常数,并对其存在性的证明、积分表示法及若干应用进行了研究.

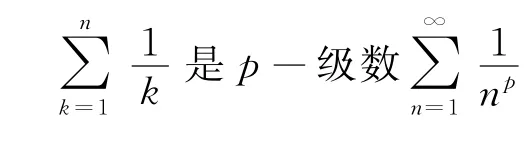
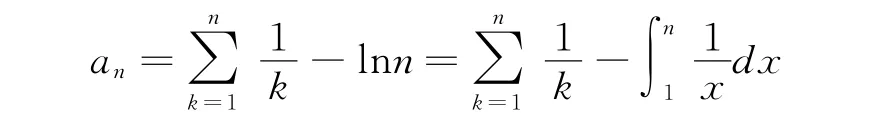
是收敛的(收敛于Euler常数).那么,

是否也收敛呢?下面我们将对此问题进行研究.
1 广义EuIer常数存在性的证明

定义将上述bn的极限称为广义Euler常数,记为cp.
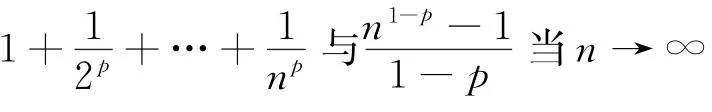
为了证明定理1,先证明如下引理.
引理对于任意实数p>0,p≠1,以及任意正整数n,有:

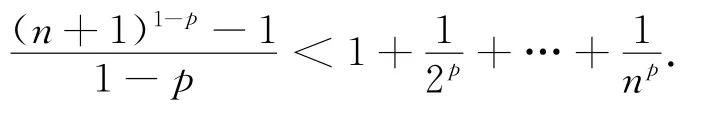
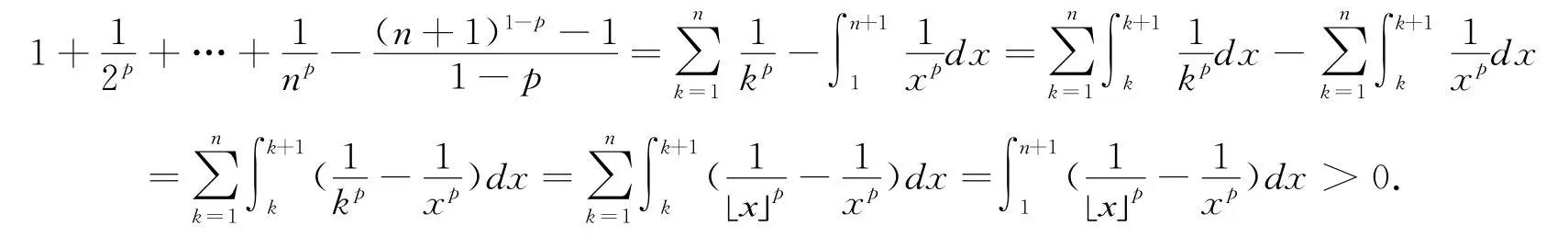
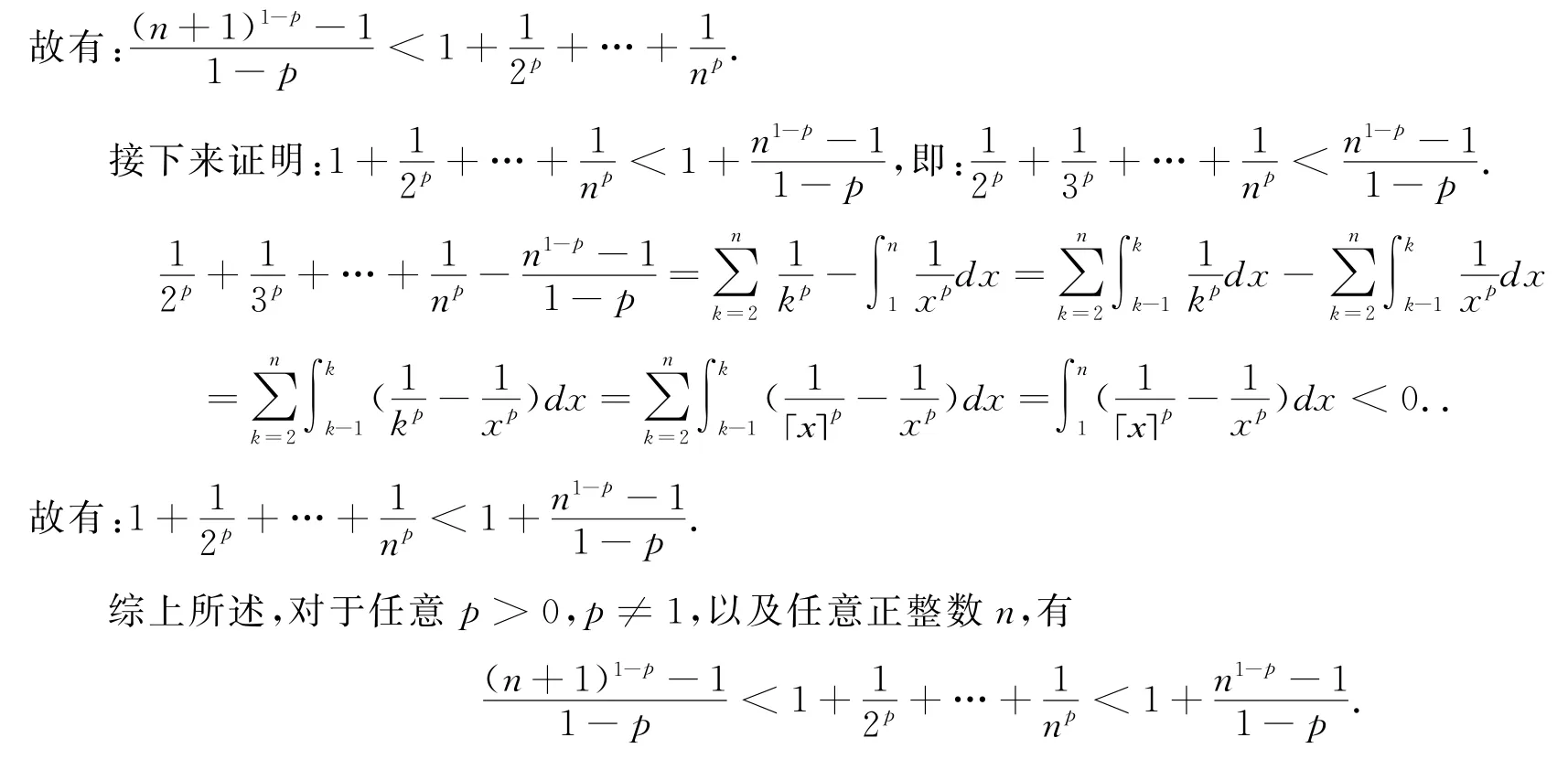
有了上述不等式,就可利用该不等式来证明定理1.
定理1的证明首先,由上述引理的证明过程可知:
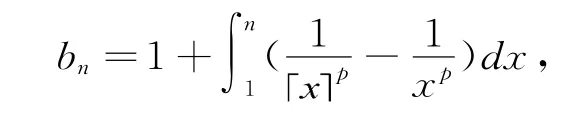
故有
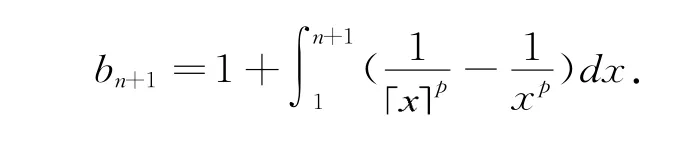
从而,
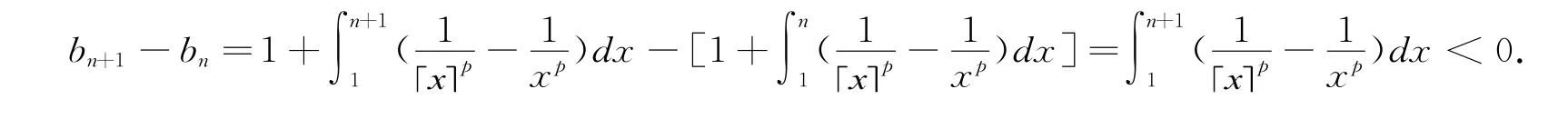
所以数列{bn}单调递减.又因为:

故有
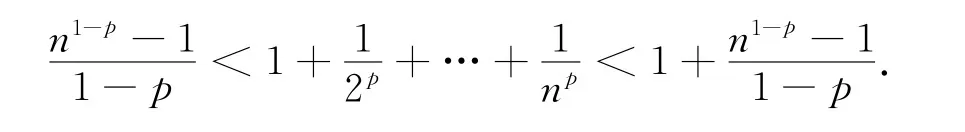
由上述证明可知,广义Euler常数cp是一个大于等于0且小于1的实数.

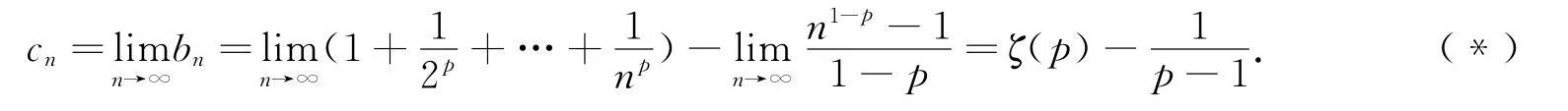
这给出了Riemann zeta函数ζ(p)和广义Euler常数cp的关系.由定理1,0≤cp<1,因此有
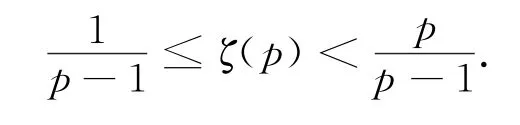

以上推论给出了一个Riemann zeta函数ζ(p)的取值范围,这对于研究Riemann zeta函数有一定意义.事实上,对于函数ζ(p),全世界数学家们已经进行了大量研究,但所得到的结果很少.早在Euler时代就知道当p是一个偶数时,ζ(p)是πp的有理数倍[5,6],因此是无理数.而当p是一个奇数时,研究起来就变得非常困难了,直到1979年,Roger Apéry才证明了ζ(3)是无理数,而对于大于3的奇数p,ζ(p)是不是无理数目前还是一个未解决的世界难题[7].
我们得到的这个推论,可对ζ(p)的值进行估计.例如,
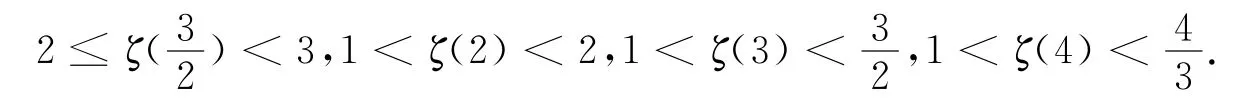
而实际上,由精确计算可知:
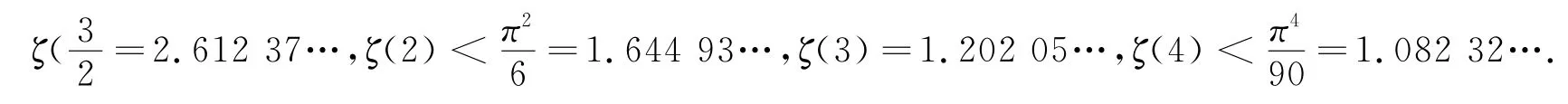
由定义易知,ζ(p)是p的减函数.此外,由推论2可知:当p≥2时,ζ(p)是介于1与2之间的一个实数,这与我们上述数值结果是相符的.并且我们有以下结论:
推论3

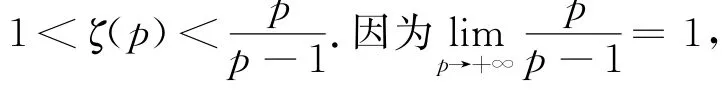
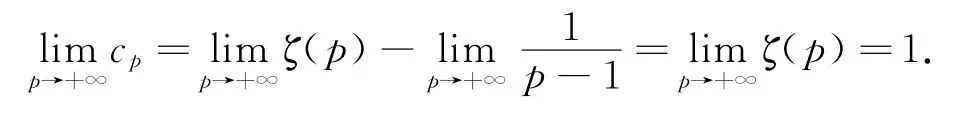
2 广义EuIer常数cp的积分表示法
定理2
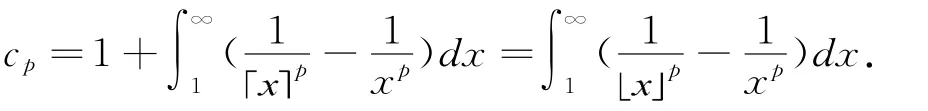
证明(i)由上述引理的证明过程有:
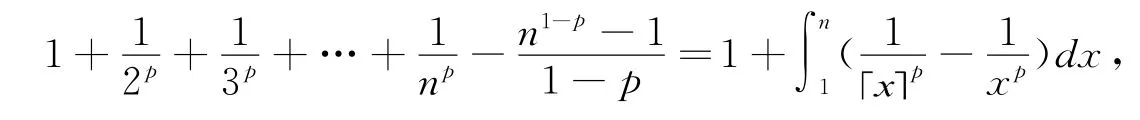
从而:
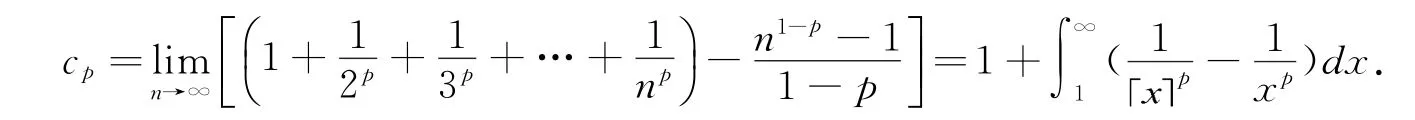
(ii)同理,由上述引理的证明过程有:
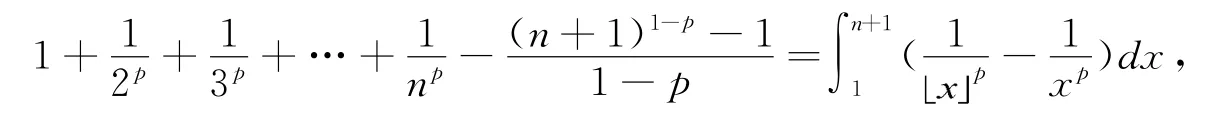
从而:
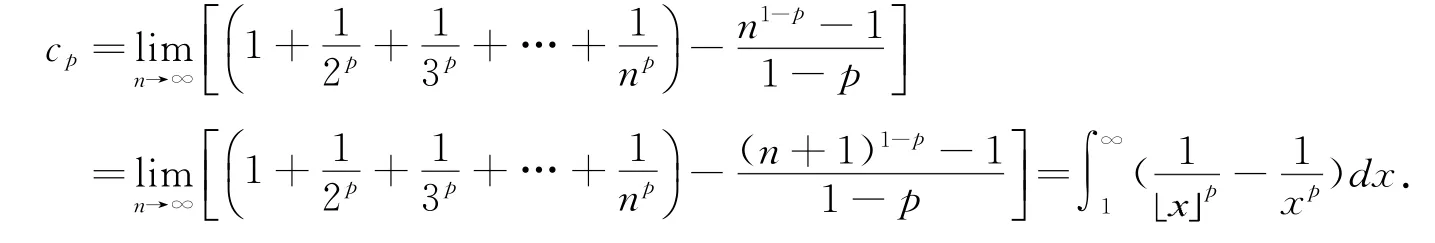
3 广义EuIer常数cp的应用
下面,我们将给出广义Euler常数cp在数项级数求和,求函数项级数收敛域和计算极限中的几个应用.
(1)确定某类级数的和
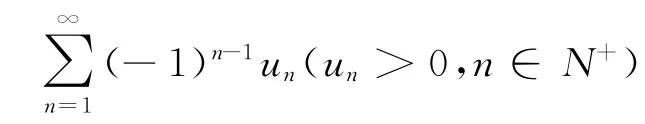
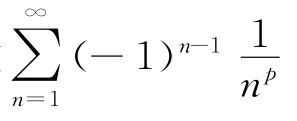
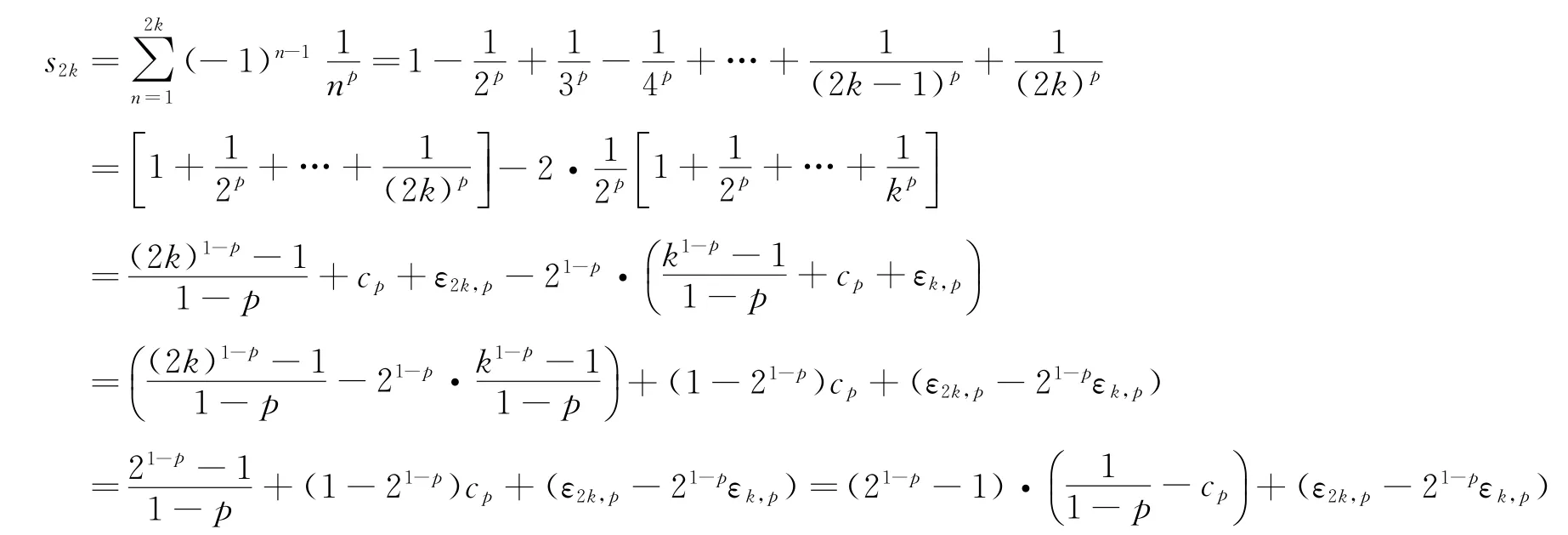
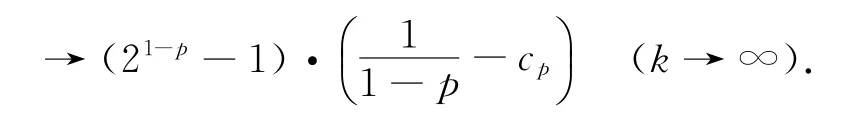
(2)求函数项级数收敛域
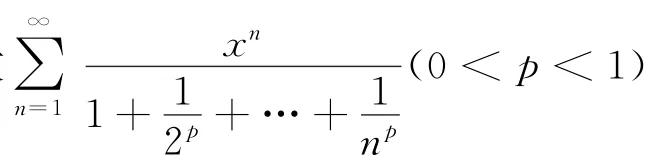
分析对于本题而言,要求其收敛域需先确定其收敛半径.
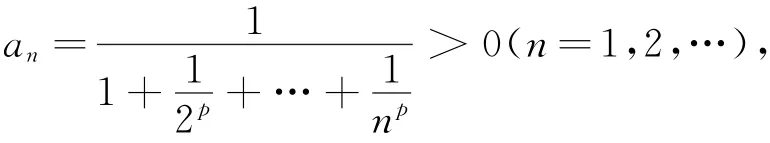
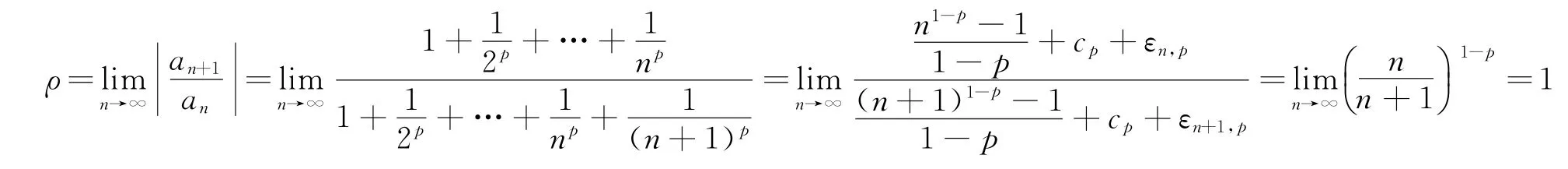
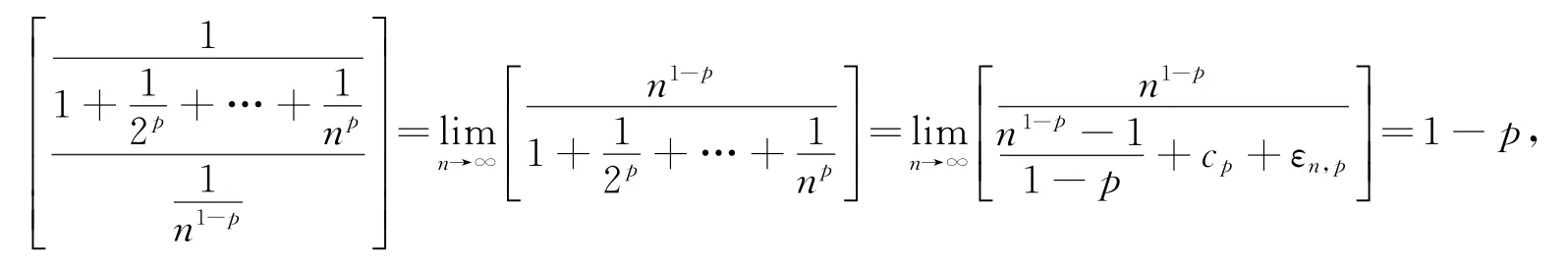
依据正项级数比式审敛法知此级数发散.
综上所述,该幂级数的收敛域为[-1,1).
注此题若假设参数p>1,也可类似讨论;若p=1,则可利用利用Euler常数进行讨论.在此就不一一撰述了.
(3)求数列极限
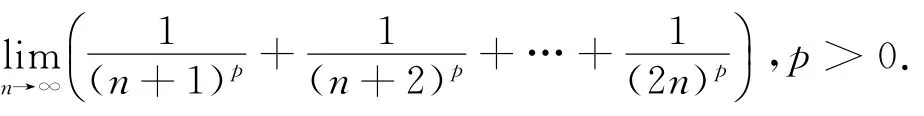
解(i)当p≠1时,

即当p>1时极限为0,当0<p<1时发散.
(ii)当p=1时,利用Euler常数得:
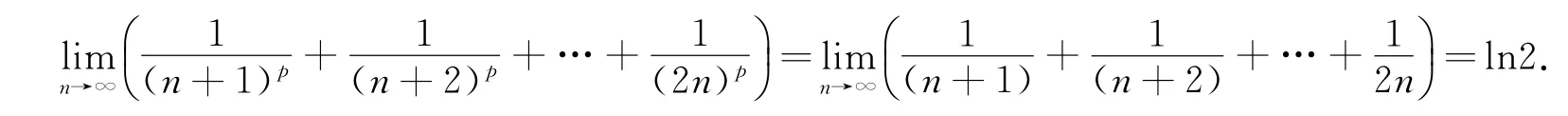
注对于当p>1时的情况,还可以用如下方法来进行证明.
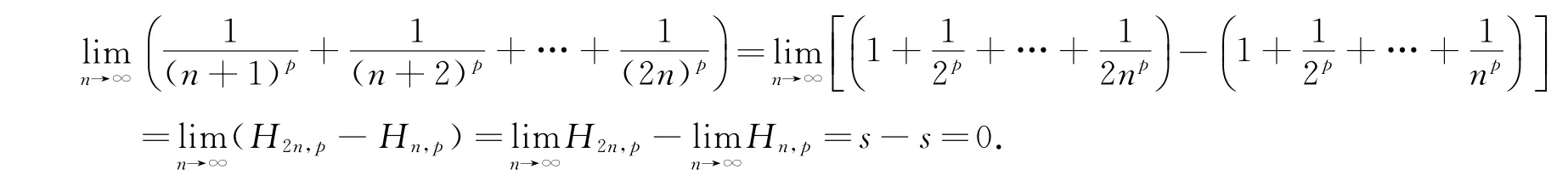
4 结束语
本文定义并研究了广义Euler常数,给出了广义Euler常数的一些性质与应用.由于笔者时间与能力所限,我们的研究还不够深入.与广义Euler常数相关的问题还有很多,比如讨论cp作为p的函数的分析学性质p(单调性、取值范围、连续性等);又如关于cp存在性证明的其他方法;还有就是广义Euler常数的其他应用等等.这一系列问题都可作为我们以后研究的课题.
[1]维基百科.莱昂哈德·欧拉[EB/OL].https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89.
[2]维基百科.欧拉-马歇罗尼常数[EB/OL].https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89-% E9%A9%AC%E6%AD%87%E7%BD%97%E5%B0%BC%E5%B8%B8%E6%95%B0.
[3]维基百科.黎曼ζ函数[EB/OL].https://zh.wikipedia.org/wiki/%E9%BB%8E%E6%9B%BC%CE%B6%E5% 87%BD%E6%95%B8.
[4]H.M.Edwards,Riemann's Zeta Function[M].Academic Press,1974.
[5]维基百科.黎曼猜想[EB/OL].https://zh.wikipedia.org/wiki/%E9%BB%8E%E6%9B%BC%E7%8C%9C% E6%83%B3.
[6]Devlin,Keith.The Millennium Problems:The Seven Greatest Unsolved Mathematical Puzzles of Our Time[M].New York:Barnes&Noble.2002:43-47.
[7]维基百科.阿培里常数[EB/OL].https://zh.wikipedia.org/wiki/%E9%98%BF%E5%9F%B9%E9%87%8C% E5%B8%B8%E6%95%B0.
The Generalized Euler Constant
LIU Yun LI Xiaolan
(School of Science,Yuxi Normal University,Yuxi,Yunnan 653100,China)
Euler constant;generalized Euler constant;mathematical constant
In this paper,the generalized Euler constant is defined,and its existence proofs,integral representations and some applications are discussed.
0173
A
1009-9506(2014)04-0001-06
2014年1月21日
刘 云,博士,教授,研究方向:代数学、组合学与理论计算机科学.

