基于DAG的Pair-Copula分解方法及其在股市相关性中的应用

蔡风景，李 元

（1．温州大学 数学与信息科学学院，浙江 温州 325035；2．广州大学a．数学与交叉科学广东省普通高校重点实验室；b．经济与统计学院，广东 广州 510006）

基于DAG的Pair-Copula分解方法及其在股市相关性中的应用

蔡风景1，2a，李 元2b

（1．温州大学 数学与信息科学学院，浙江 温州 325035；2．广州大学a．数学与交叉科学广东省普通高校重点实验室；b．经济与统计学院，广东 广州 510006）

采用图形建模工具中的有向非循环图（DAG）方法对高维随机变量进行Pair-Copula分解，并提出非正态的PC算法对DAG进行识别，最后应用于国际股市分析主要股指的尾部相依结构。数值模拟表明，若变量不服从椭圆分布，新的非正态PC算法要优于传统的PC算法。经AR（1）-GARCH（1，1）模型过滤后的残差DAG分析，股市信息流动具有明显的区域效应，欧洲股市主要通过美国与美洲其它股指存在信息传导。英国和香港是欧洲和亚洲股市信息联系的纽带，中国内地只与香港存在直接的信息流动。基于SJC-Copula实证结果表明，欧洲德国和英国股市间的尾部相关性较强，亚洲股市间下尾相关系数要大于上尾，不同区域联结股市间的上尾相关性强于下尾。

DAG；Copula函数；SJC

一、引 言

1959年Sklar首先提出Copula理论，并指出随机变量的联合分布可分解为边际分布和描述变量相关性的Copula函数。因此，若确定变量的边缘分布和选定一个合适的Copula函数后，就可以方便地给出随机向量的联合分布［1］1－15。由于Copula函数在使用中对边际分布的选择没有限制，因此可以运用Copula函数理论灵活构造多元分布，这是传统联合分布无法比拟的优势。同时，Copula函数的参数估计可以分阶段进行，解决了许多参数需同时估计的困难，大大降低了模型参数估计的复杂程度。

理论上Copula函数可简单推广到高维情形，但遗憾的是现有Copula函数绝大多数为二元Copula，大大限制了该方法在高维建模中的应用。因此，对高维Copula函数的构造研究也成了学术界关注的热点问题。Bedford等提出使用Pair-Copula分解方法对高维Copula进行降维，该方法通过高维随机变量密度函数的分解，将高维问题分解成若干个二元 Copula函数建模问题［2－3］。Kurowicka等采用了基于树结构的高维Copula分解方法［4－5］。国内的杜子平等将高维Copula建模中藤的方法与动态Copula相结合，构造了基于藤方法的高维动态Copula，且将该方法应用于国际股票市场，研究其动态相关性［6］。张高勋等构建基于藤的Pair-Copula方法应用于国内行业股指的VaR计算［7］。由于基于藤的Pair-Copula方法对相关结构有较强的假定，因此推断有一定的主观性。近年来，有向非循环图（Directed Acyclic Graph，DAG）被广泛应用于经济领域进行相关结构的统计推断，因此基于DAG的Copula方法也被提出应用于高维分解，但遗憾的是在上述研究中DAG是经验给定［8－11］。本文提出非正态的PC算法对过滤后残差的DAG进行统计推断，这种基于数据的驱动方法要优于主观设定的经验方法，再利用基于DAG的Pair-Copula分解方法分析国际主要股指的尾部相依结构。

二、基于DAG方法的Pair-Copula分解

（一）Pair-Copula基本理论

边际分布在［0，1］区间上均匀分布的Copula函数刻画了联合分布与边缘分布之间的依赖结构。

因此，多元密度函数可通过若干个条件密度函数的二元Copula函数的乘积进行构建，实际上该分解过程为迭代运算。

（二）基于DAG方法的Pair-Copula分解

对于有向非循环图D＝ ｛V，E｝，V是点集，表示随机变量的集合，E（ V×V）为有向边集合，两点间至多有一条边。令pa（v），de（v），nd（v）分别表示点v父结点、后代和非后代集，记为：

假定有向非循环图D满足因果Markov和忠实性假设两个假设，则任一分布P都可按照D中的父子结构分解为［12］：

下面以五个变量为例，对基于DAG的Pair-Copula密度函数分解进行说明。

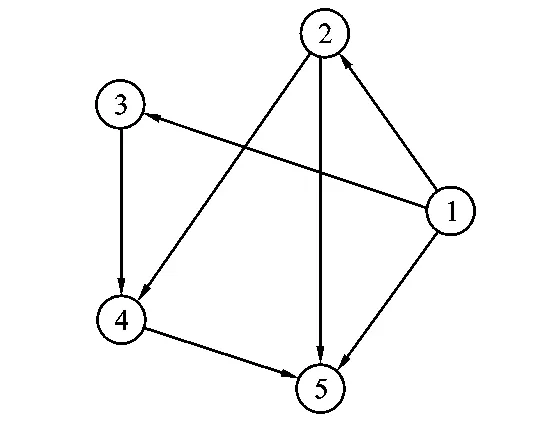
图1 示例DAG

根据式（7），可将图1中的联合密度函数表示为：

目前，大部分学者主要通过PC算法对DAG进行识别，但传统的PC算法要求序列为正态分布，而实际的金融时间序列往往并不服从正态分布，因此本文提出基于非正态分布的PC算法识别DAG，其思想是：若随机向量不服从多元正态分布，先利用非参正态方法将其变化为正态分布再进行识别［12－13］。

（三）边际分布和Copula选择

由于金融时间序列数据通常表现出尖峰、厚尾和偏斜的特性，因此在边际分布选择上，除沿用经典的GARCH类模型外，本文利用能同时体现数据的尖峰、厚尾和偏斜特性的偏斜－t分布来刻画残差序列的分布［14］。偏斜学生t分布的密度函数如下：

由于股票收益率数据一般会表现出波动聚集性，利用 AR（1）-GARCH（1，1）模型来描述股指收益率，误差项通过偏斜t分布刻画，参数采用极大似然方法进行估计。

三、非正态PC算法有效性的数值模拟分析

为检验非正态PC算法的有效性，分别基于6维和9维随机变量进行数值模拟。为保证模拟的稳健性，随机产生1 000个DAG，对每个DAG图形均随机产生1 000次正态分布、t分布、混合正态分布和Cauchy分布序列长度为1 000的样本数据，分别利用传统的PC和非正态的PC算法进行识别。由表1模拟结果可知，模拟维数为6时，基于传统PC算法的各种分布的平均正确识别率差异不大，但正态和t分布下平均错误识别率要明显小于混合和Cauchy分布，同时导致基于前两种分布的平均正确发现率要好于后两种分布。利用新的非正态PC算法发现4个分布三种指标识别效果均较佳，算法对分布比较稳健。在正态和t分布下，新算法和传统的PC算法差异不大，但在混合正态分布和Cauchy分布下，新的非正态PC算法的平均错误识别率明显要小于传统的PC算法，从而说明新的算法识别效果更好，对分布更加稳健。当模拟的维数增加到9维时，可以得到类似的结论。同时，当维数增加时，虽然平均正确识别率略有提高，但是平均错误识别率提高更快，总体识别效果下降。

表1 数值模拟结果（6维和9维）

四、实证分析

由表2各股指收益率的统计指标可知，日收益率均值都在0附近。所有股指收益率的偏度均小于0，即股指收益率的分布左偏。各股指收益率的峰度均大于3，说明股指收益率具有尖峰厚尾性。Jarque-bera正态性检验表明上述股指收益率均显著拒绝正态假设。Q6和Q26统计量表明，美国、加拿大、德国和台湾股指收益率有一定的自相关性，股指收益率平方均存在显著的自相关，证实波动率聚集现象。

由上述基本统计性质可知，上述股指收益率数据ARCH效应显著，分布呈明显的尖峰厚尾和偏斜性，因而采用 AR（1）-GARCH（1，1）模型对数据的边际分布进行建模，其中误差项利用偏斜t分布来拟合。对建模后得到的标准残差序列进行ARCH效应检验，结果拒绝ARCH效应，表明标准残差序列已无二阶相关性，GARCH建模效果良好。

对经 AR（1）-GARCH（1，1）模型过滤后的标准残差序列利用柯尔莫格洛夫和Shapiro-Wilk进行正态性检验（表3），发现大部分标准化后的残差序列不服从正态分布，因此采用非正态的PC算法进行DAG（图2）识别。

由图2可知，欧洲德国和英国股市存在直接的联结，美洲和亚洲各国或地区股指内部存在相互的信息流动，说明国际股市信息流动存在明显的区域效应。美国和欧洲股指的信息传导需通过美国股市，这是因为美国股市在美洲乃至全球股市均起着举足轻重的作用。欧洲和亚洲股指的信息流动需通过英国和香港股市作为中介，这主要是因为香港是新时代亚洲金融中心，在亚洲与世界股指信息流动中起着重要的联结作用。中国内地只存在与香港股市的有向边连接且为有向边的终点，说明香港对中国内地股市有一定的信息传导，中国内地股市虽然和全球股市联动性逐步增强，但香港股市还是其联动的重要纽带。同时，再利用传统的PC算法进行DAG识别，除个别有向边指向不同之外，其余有向边与图2完全一致，这也说明非正态的PC算法比较稳健。

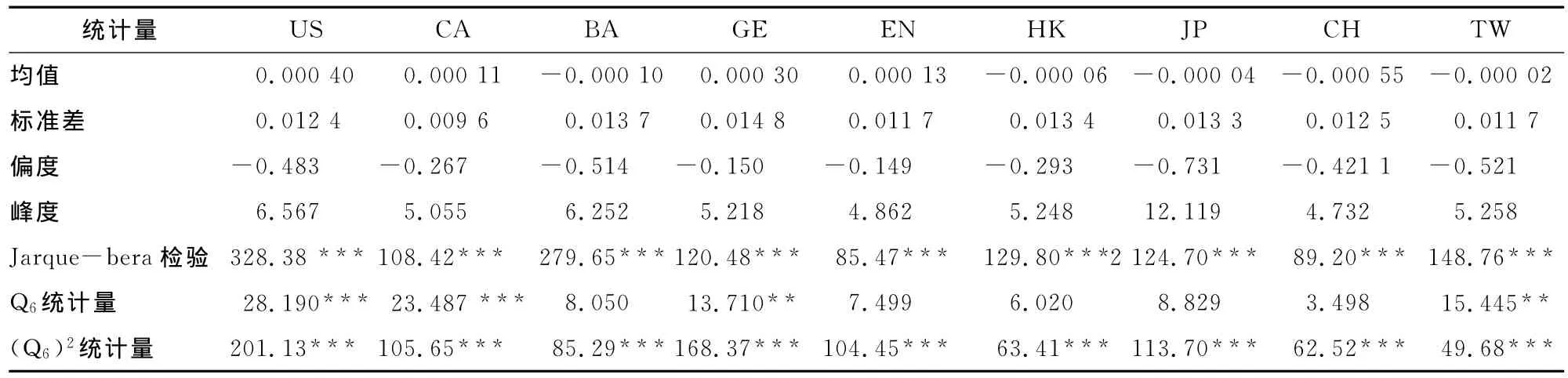
表2 各股指收益率基本统计性质

表3 残差（标准化）的正态检验

图2 国际主要股指收益率的DAG

根据图2的DAG结果，基于SJC Copula方法进行高维Pair-Copula分解：

表4给出了式（13）中相应Copula函数的尾部相关系数的估计结果。由尾部相关系数可知，国际主要股指收益率的尾部相关性系数较大，欧洲德国和英国股指之间的尾部相关性最强，最容易导致暴涨暴跌的情形发生。美洲美国和加拿大股市尾部相关性较强，美国和巴西股指尾部相关性较小，不超过0．1，加拿大和巴西的条件尾部相关系数接近于0，说明巴西和其它主要美洲股指同时暴涨暴跌的可能性较小。亚洲股指内部中国内地和香港、日本和台湾的下尾相关系数均大于上尾，说明同时暴跌的可能性要大于暴涨。不同区域（洲与洲）国家或地区股市之间的上尾相关系数大于下尾（美国－德国；英国－香港），同时暴涨的可能性要大于暴跌。

表4 基于SJC copula高维Pair分解的尾部相关系数

五、结 论

本文基于DAG方法对高维Copula进行Pair-Copula分解。该分解方法允许双变量Copula之间可灵活建模，自由选择不同类型的Copula函数。相比较以前基于藤结构的Copula方法，本文采用的方法在参数估计和模型构造上更节约，效率更高。同时，本文采用非正态PC算法对DAG进行统计推断，克服了以往只依赖主观及经验设定、过分依赖正态假设的不足，应用范围更广。将该方法应用于国际主要股票市场分析主要股指收益率的相依结构，DAG识别结果表明，美洲、欧洲和亚洲内部股指信息流动顺畅，国际主要股指信息传导具有明显的区域效应。中国和国际股市的信息传递还是需通过香港股市。基于SJC－Copula函数的Pair－Copula分解结果表明，国际主要股指的尾部相关性较强，尤其是欧洲德国和英国股市。亚洲股市间的下尾相关性要强于上尾，而不同区域国家股市间的尾部则恰好相反。由于图模型理论在高维数据降维中具有独特优势，因此可以预见图模型在Copula理论的Pair分解中应该大有可为，这也是本文未来要深入研究的问题。

［1］ 韦艳华，张世英．Copula理论及其在金融分析上的应用［M］．北京：清华大学出版社，2008．

［2］ Bedford T，Cooke R M．Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines［J］．Annals of Mathematics and Artifcial Intelligence，2001，32（1）．

［3］ Bedford T，Cooke R M．Vines－A New Graphical Model for Dependent Random Variables［J］．Annals of Statistics，2002，30（4）．

［4］ Kurowicka D，Cooke R M．Sampling Algorithms for Generating Joint Uniform Distributions Using the Vine -copula Method［J］．Computational Statistics and Data Analysis，2007，51（6）．

［5］ Aas K，Czado C，Frigessi A，et al．Pair-Copula Constructions of Multiple Dependence［J］．Insurance：Mathematics and Economics，2007，44（2）．

［6］ 杜子平，闫鹏，张勇．基于“藤”结构的高维动态Copula的构建［J］．数学的实践与认识，2009，30（10）．

［7］ 张高勋，田益祥，李秋敏．基于Pair-Copula模型的资产组合VaR比较研究［J］．系统管理学报，2013，22（2）．

［8］ Yang J，Guo H，Wang Z J．International Transmission of Inflation among G-7Countries：A Data-determined VAR Analysis［J］．Journal of Banking ＆ Finance，2006，30（10）．

［8］ 杨子晖．财政政策与货币政策对私人投资的影响研究——基于有向无环图的应用分析［J］．经济研究，2008（5）．

［9］ 蔡风景，蔡周策，李元．基于DAG方法的经济变量因果关系研究［J］．统计与信息论坛，2008，23（9）．

［10］Czado C，Min A，Baumann T，et al．Pair-Copula Constructions for Modeling Exchange Rate Dependence［R／OL］．［2013－11－20］．http：／／wwwm4．ma．tum．de／Papers／Czado／cc－pubs．html．

［11］Bauer A，Czado C，Klein T．Pair-Copula Constructions for Non-Gaussian DAG Models［J］．Can J．Statistics，2012，40（1）．

［12］Spirtes P，Glymour C，Scheines R．Causation，Prediction and Search［C］．Proceedings of Adaptive Computation and Machine Learning．Cambridge：MIT Press，2000．

［13］Liu H，Han F，Yuan M，et al．High Dimensional Semiparametric Gaussian Copula Graphical Models［J］．Ann．Stat．2012，40（40）．

［14］Hansen B E．Autoregressive Conditional Density Estimation［J］．International Economic Review，1994，35（3）．

［15］Patton A J．Modeling Asymmetric Exchange Rate Dependence［J］．International Economic Review，2006，47（2）．

Pair-copula Constructions with DAG and Application on the International Stock Markets

CAI Feng－jing1，2a，LI Yuan2b
（1．School of Mathematics ＆Information Science，Wenzhou University，Wenzhou 325035，China；a．Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institutes；b．School of Economics and Statistics，2．Guangzhou University，Guangzhou 510006，China）

The Pair-Copula constructions based on directed acyclic graph which is distinguished by Nonnormal PC algorithm is proposed and used in the dependence structure among the international stock markets．Simulation shows that the Nonnormal PC algorithm is superior to the traditional method．Empirical result shows that the regional segmentation of the major international financial markets is proved in this study，the connection between America and European stock markets by US；the connection between European and Asian stock markets by England and Hong Kong；Chinese stock market is only connected Hong Kong directly．The tail dependence between German and England stock markets is the strongest the lower tail dependence between Asian stock markets is stronger than the upper，while the upper tail dependence between different continents is stronger than the lower．

directed acyclic graph；Copula function；SJC

O212∶C812

A

1007－3116（2014）06－0048－06

2013－11－18

国家自然科学基金项目《一类半参数时间序列模型的统计推断》（11271095）；教育部人文社会科学基金项目《图模型方法在金融计量中的应用》（12YJCZH002）；高等学校博士学科点专项科研基金《一类非平稳变系数部分线性时间序列模型的研究》（20124410110002）；国家统计科研计划一般项目《基于图模型方法的大数据处理技术及应用研究》（2013LY136）；数学与交叉科学广东省普通高校重点实验室开放课题资助项目《经济计量中高维数据的图模型建模及应用》（2012－02－03－01）

蔡风景，男，浙江瑞安人，管理学博士，副教授，研究方向：数量经济和金融统计；

李 元，男，山东临沂人，概率统计专业博士，教授，博士生导师，研究方向：金融统计和风险管理。

（责任编辑：崔国平）