基于模糊数学的高校辅导员工作综合评价模型

王立新1，张少玮

(1.安徽建筑大学 电子与信息工程学院，安徽 合肥 230601；2.广州大学 旅游学院，广东 广州 510006)

1 前言

高等学校很重要的一项工作就是学生工作。而做好学生工作是辅导员工作的中心任务，但对辅导员工作的考评却是一项棘手的问题。在笔者学习和工作的几所高校中，通常的考评只是制定好几个考察指标，让学生去勾画，再进行统计，最后按照指标加权得出排名顺序。这样的评判方式主要依靠主观经验，采用定性为主的手工评判方法，对所规定的硬性指标进行经验化、主观化的判断来完成测评指标的制定和指标权值的确定，而最终的评判结果常常不能很好地全面地反映辅导员工作的情况。

当前对于辅导员工作的评价方法研究的重点：(1)对评判准则的制定，(2)对于评价对象选择何种评价模型，(3)评判数据的处理方法。比如，有的评判是侧重于制定规范化的授奖规则与评价流程，有的则是建立了评价模型和评判标准把定性和定量方法相结合，以便体现出较高的科学性、公正性和权威性。

现实中，对辅导员的考评由于其评判因素的权重和评语都是不明确的，完全定量考察辅导员工作不太现实，但可以尽可能地减少评判指标和权值的主观性是研究工作所追求的目标。为此我们在对学生进行不同年级多批次调查统计的基础上，采用定性化评价与定量化分析相结合的规范方式和方法对辅导员工作进行科学、公平和合理的评价，对采集的评判数据采用模糊数学的相关概念来进行处理。基于上述理念，我们开发了一个实用的学评辅应用系统，对我们的研究工作作了一次实践尝试，也是对高校的辅导员工作的评判进行一次有意义的探索，对评判方法的研究具有一定的理论价值和应用价值。

2 模糊综合评判方法

不同的评判评估领域有多种不同的评判评估方法，其中模糊综合评判方法是应用最为广泛的。

2.1 单因素模糊评判方法

对于包含评判因素较少的评判对象来说，可采用单因素模糊评判模型。主要由以下6个主要步骤构成:

(1)确定因素集X(x1,x2,…,xm), 它是被评判对象各因素组成的集合，也可以称被评判对象的m个属性；

(2)确定评价集Y(y1, y2,…,yn), Y是评语组成的集合，它表示因素可能取得评价，模糊评价就是Y上的一个模糊集；

(3)由于各因素在整个评价体系中的重要性未必相同，所以需对各因素加权，可用X上的模糊集A表示各因素的权数分配；

(4)现假定对每个因素xi都有一个模糊评价Ri={ri1,ri2,…，rin，对m个因素有m个模糊评价Ri(i=1,2,… m)，可以确定一个模糊关系矩阵Rmⅹn表示，称R为评判矩阵，这个矩阵也叫做单因素评判矩阵。

(5)将权数模糊集A与评判矩阵R合成，得到对各因素的综合评判B，它是Y上的模糊集。其运算的形式：

B=AoR

这里“o”代表合成运算。在广义模糊运算下B的各元素为

bj=(a1☆r1j)★(a2☆r2j)★…★(am☆rmj) (1<=j<=n)

这里“☆”代表广义模糊“与”运算，“★”代表广义模糊“或”运算。

(6)针对B给出综合评判结论，其中bj可以按下面具体的有六种可选方法或其他方法计算得出。

(Ⅰ) bj=max{min(a1,r1j),min(am,rmj)}

(Ⅱ) bj=max{a1r1j}

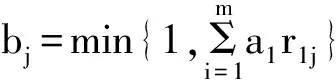
2.2 多层次综合评判方法

以上是模糊综合评判的基本模型，是基于单因素的模糊评判。但在实际运用中，往往评判的因素很多，此时更合理、更准确应为多级的综合评判。其具体的步骤分为三步：

首先，对评判的因素进行划分，将其划分为k个子集，即X={X1，X2，…，XK}，并且要求：

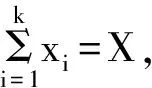
第二，对于每个Xi的mi个因素，按上面提到的单因素评判的六种可选方法之一进行计算，得单因素评价结果：

Bi={bi1,bi2,…，bin}=AioR

其中Ai={ ai1,ai2,…，ain}(1≤i≤k)

第三，把每个Xi作为一个因素，Bi作为的Xi单因素评价，按第二步中的评价法进行综合评价，得到

B={ b1,b2,…，bn}= AoR，

其中A={a1,a2,…，ak},R=[B1，B2，…，BK]T=(bij)kn,则可由A与R求得二层次综合评价B。

若要再对Xi划分，则可得三层以至更多层次的综合评价模型。

考评辅导员的指标体系总的说起来比较多，可以分成二个或更多个层次比较好，这样综合评判应按各个层次分别进行，构造多级评判模型。

3 辅导员评价指标模型的建立

3.1 辅导员考核指标的分析

如在辅导员的综合评判中，指标体系可首先按照品德、能力、表现和业绩分为第一层次，然后分别四个一级指标划分二级指标。因此，先分别对品德、能力、表现和业绩按上述的单因素评判模型展开评判，得到B1、B2、B3、B4，然后，设计品德、能力、表现和业绩的相对权重，按上述模型进行二级评判，得到总的综合评判B。当然，综合评判是一项决策工作，应采用成立一个评估小组对考核指标的确定、指标的权重、判断集的评语、数据的采集方式和综合评判结论的最终确定等方面进行深入研究，力求做到尽可能的客观。

辅导员考核指标的确定是一个关键性的问题，不同的人会有不同的指标内容。但总的来说相差不大。笔者在原单位当过辅导员，开发过学评辅系统软件。据此经验考核指标大致如图1。

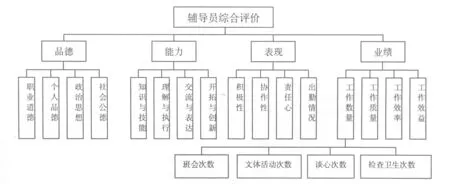
图1 考核指标层次图

3.2 辅导员考核指标权重的确定

在上节“辅导员考核指标的分析”中我们提到指标的权重要尽可能地合理，这是另外一个话题，在此不再讨论。对于工作量化评价需要考察班会、文体活动、谈心和检查卫生的次数和参与度等情况来给予认定。我们给定这几个权重如下：

表1 权重和评语表

续表1 权重和评语表

3.3 数据示例

针对以上的指标体系和有关的权重与评语标准数据，可以得出评判的结论。具体运算过程如下：

先计算最下一级的指标，可以得出上一级评价向量。限于篇幅，在此只是介绍如何用班会、文体、谈心和查卫生这四个三级指标来计算工作量化这个二级指标的评价向量的过程，其他高一级的指标的评价向量的计算过程类似。

B= {b1,b2,b3,b4}={0.325, 0.385, 0.23, 0.06}

这时，可以把B中的元素作为二级指标工作量化的评语标准的参数来参与求一级指标业绩的评价向量。当一级指标的所有因素的评价向量都按本节中的步骤求出后，最后来求辅导员综合评价的评价向量，①可按最大从属函数判别原则，该向量中最大值为；②按转化百分制计算结果；③按最大接近度判别，等等。可以综合几种计算结果，最终得出对该辅导员的综合评价。

4 有关问题的讨论

采用上述的综合评判模型有两个问题需要特别重视:(1)评判指标体系的建立。指标一般分为两种，一种属于主观效用指标，另一种属于客观定量指标。评判指标体系的建立需要遵循一条基本的原则，就是尽量少一点主观性，多一点客观性，以便降低评价结果的主观成分。(2)评价的科学性和公正性:如何确定评判过程中所需要的权重向量和模糊关系矩阵对于评价结果的科学性和公正性具有重要意义。关于权重向量和模糊关系矩阵的确定方法有多种，但是仍然值得深人讨论。

从整个过程来看，还有若干方面有待研究：评判指标的权重、评判的评语集、数据的采集方式和综合评判结论的最终确定等，力求做到尽可能的客观。尽管基于模糊理论，但是除了在多个方面是模糊的外，其它方面还是精确的。这一方面可以说是尽量消除主观性，但是却失去了模糊理论的彻底性。

我们在现实中也遇到一些实践性的问题：(1)采集：现实中采用何种途径和技术手段能方便和广泛地收集评判数据。(2)处理：怎样才能识别不同收集数据的途径和方法产生的噪音数据，对某些重要的数据在采集时需要采用何种技术进行正确性保障，对收集起来整理后的数据，采用何种机制和技术方法进行核实，同时对某些遗漏、偏离合理范围的数据等做怎样的处理。(3)整合：通过不同的收集途径和方法获取的数据如何和评判目标结合起来，对收集的数据如何进行整合等。

20世纪90年代中期，随着数据仓库技术的迅速发展，基于数据挖掘的评判方法也逐步得到研究和应用。

5 结束语

本文借鉴了他人研究的一些方法成果，针对高校辅导员工作评判，把模糊评判方法应用到辅导员工作评价应用系统。尽管还有不少需要加强研究和细化的地方，但在总体结果上，基本能真实反映辅导员实际的工作表现，说明此种方法在建立辅导员绩效考核指标体系以及绩效评判方法方面是有效的。 为辅导员的学生工作提供了重要的参考，也为领导决策提供较为科学的决策依据。

参考文献：

[1] 谢季坚,刘承平.模糊数学方法及其应用[M].武汉：华中科技大学出版社,2013.

[2] 刘合香.模糊数学理论及其应用[M]. 北京：科学出版社,2012.

[3] 王新民,谢盛青，等.基于模糊数学综合评判的采空区稳定性分析[J].昆明理工大学学报(理工版)，2010,35(1):9-13.

[4] 任贵红,张苗，等.基于模糊数学和灰色关联分析的化工储罐区火灾风险评估研究[J].中国安全生产科学技术，2013,9(2):105-111.

[5] 林慧.基于模糊数学的高校教学质量评价系统[J].湖南理工学院学报(自然科学版),2012,25(4):25-27，61.

[6] 危子青，王清玲.项目教学法与高职数学建模教学的改革[J].职教论坛，2013,(35)：76-78.