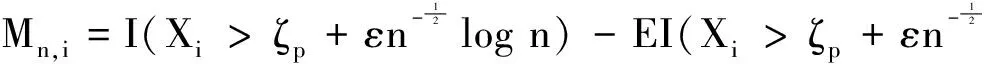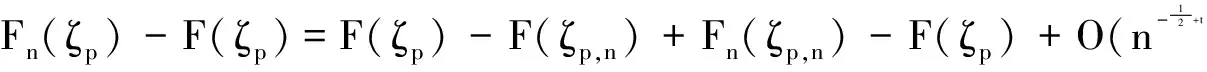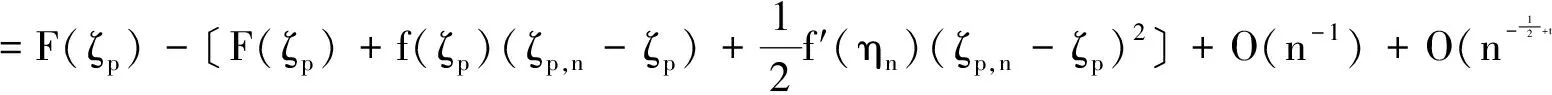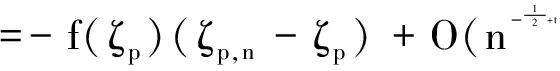混合序列下分位数估计的强相合及其Bahadur 表示
张文婷1,蔡际盼1,李永明
(1.广西师范学院 数学科学学院, 广西 南宁 530023;2.上饶师范学院,江西 上饶 334001)
引言
设{Xn; n≥1)是概率空间(Ω;F;P)上的随机变量序列, 具有相同的分布函数F(x)=P(X≤x).对于p∈(0,1),定义ζp=inf{x:F(x)≥p}为F(x)的p阶分位数, 记为F-1(p),其中函数F-1(t)(0 定义记Fu=σ(Xi,i∈u⊂N),N为自然数集.L2(Fu)表示所有Fu可测且二阶矩有限的随机变量全体,d(u,v)表示有限子集u和v的距离,令 下面我们给出一些基本假设: (A2) F(x) 在ζp的某个邻域Np内可导,密度函数满足0 本文的主要结果如下: 定理1 假设(A1),(A2)成立,log n 表示以2为底的对数,当n→∞时, 有 定理2 满足引理5和定理1的条件,当n→∞时, 有 下面我们给出本文所需引理. 引理2[11]设F(x)是右连续的分布函数,则广义逆函数F-1(t), 在0 (1) F-1(F(x))≤x,-∞ 引理3[12]令p∈(0,1),ζp,n=Fn-1(p)=inf{x:Fn(x)≥p},假设P(Xi=Xj)=0,i≠j. 那么 证明由于Fn(x) 是非降函数, 可得 =D1+D2. (3.1) (3.2) 根据微分中值定理, 有 (3.3) 因此, 由(3.1)-(3.3) 可得 引理得证. 引理6 满足引理5的条件, 当n→∞时, 有 证明根据引理5可得 引理证毕. 定理1的证明令k≥1, 根据子序列法要证结论成立只需证明 (4.1) 下面我们来证明(4.1)式. 由于 =H1+H2. (4.2) 根据引理2,引理3,引理4和Markov不等式以及Taylor 公式, 有 (4.3) (4.4) 因此, 由(4.2)(4.3)(4.4)式可得 故根据Borel-Cantelli 引理可得(4.1) 式成立, 从而该定理得证. 定理2的证明根据引理3, 有 Fn(ζp,n)-p=O(n-1),a.s.. (4.5) 由引理6可得 (4.6) 从而, 根据(4.5)(4.6) 式和定理1以及Taylor 公式可得 其中ηn是介于ζp,n与ζp之间的随机变量. 整理上式可得 定理证明完毕. 参考文献: [1] Shuxia Sun. The Bahadur representation for sample quantiles under weak dependence [J]. Statistics and Probability Letters, 2006, 76: 1238-1244. [2] Ajami M., Fakoor V., Jomhoori S. The Bahadur representation for kernel-type estimator of the quantile function under strong mixing and censored data [J]. Statistics and Probability Letters,2011, 81(8): 1306-1310. [3] Guodong Xing, Shanchao Yang, Yan Liu, Keming Yu. A note on the Bahadur representation of sample quantiles for α-mixing random variables [J]. Monatshefte für Mathematik, 2012, 165:579-596. [4] Qinchi Zhang, Wenzhi Yang, Shuhe hu. On Bahadur representation for sample quantiles under α-mixing sequence [J]. Statistical Papers, 2012. [5] Guodong Xing, Shanchao Yang. A remark on the Bahadur representation of sample quantiles for negatively associated sequences [J]. Journal of the Korean Statistical Society, 2011, 40(3): 277-280. [6] 梁丹, 杨善朝, 蒙玉波. NOD 序列样本分位数的Bahadur 表示[J]. 工程数学学报, 2013, 30(1): 77-84. [7] 吴群英. 混合序列的概率极限理论[M]. 北京: 科学出版社, 2006. [9] Yongfeng Wu, Chunhua Wang, Andrei Volodin. Limiting behavior for arrays of rowwise ρ*Mixing random variables[J]. Lithuanian Mathematical Journal, 2012, 52(2): 214-221. [10] Mingle Guo, Dongjin Zhu.Complete convergence of weighted sums for ρ*mixing sequence of random variables[J]. Journal of Mathematical Research with Applications, 2013, 33(4): 483-492. [11] Serfling R.J. Approximation theorems of mathematical statistics [M]. New York: John Wiley and Sons, 1980. [12] Xuejun Wang, Shuhe Hu, Wenzhi Yang. The Bahadur representation for sample quantiles under strongly mixing sequence [J]. Journal of Statistical Planning and Inference, 2011, 141: 655-662. [13] Sergey Utev, Magda Peligrad. Maximal inequalities and an invariance principle for a class of weakly dependent random variables[J]. Journal of Theoretical Probability, 2003, 16(1): 101-115.



1 基本假设和结论

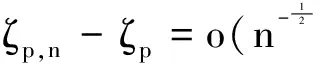
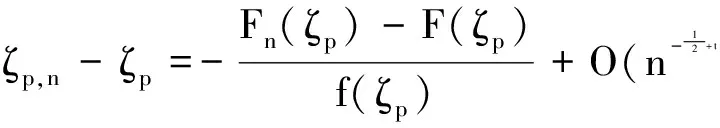
2 辅助结论






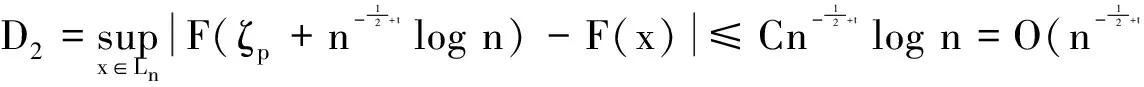
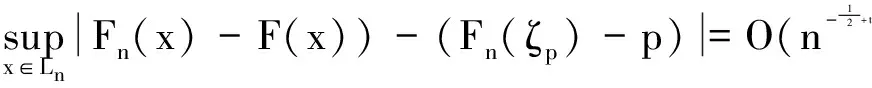
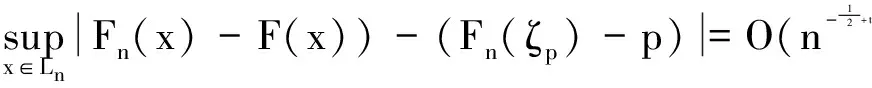

3 主要结论的证明