奇异迁移算子一阶余项的弱紧性

(上饶师范学院，江西 上饶 334001)

1 引言

本文考虑以下奇异迁移方程的初值问题：

(1)

其中H为正有界线性算子，即平行板的左右面上的周期边界算子，即

φ(a,v,μ)=φ(-a,v,μ),0<μ<1;φ(-a,v,μ)=φ(a,v,μ),-1<μ<0

(2)

假设：(O1)σ(v)和k(v,м,v′,μ′)分别为E和G×G(G=E×[-1,1])上的可测函数，且存在具有零测集的闭子集E0⊂E和常数σ0>0，使得

σ(·)∈L∞(EE0),σ(v)≥σ0,a,e,v∈E

(O2)算子K是正则的，即如果K限制在L1(G)是弱紧正的。

对迁移方程解的渐近性态和迁移算子的谱分析研究是迁移理论研究的主要问题之一，自从Lehner.J.Wing.G.M和Jorgeas的开创性工作以来，迁移算子的研究已成为数学界、物理界及工程技术界都非常感兴趣的问题。近年来，对一般迁移算子的谱研究工作较多(即见文献[3-7])，但对奇异迁移算子及迁移方程的讨论较少。其中K.Latrach与M.Kokhtar-Kharroubi在L1空间，讨论了板几何中一类具反射边界条件的奇异迁移方程，证明了该半群V(t)的Dyson-Phillips展开式的二阶余项R2(t)的弱紧性。由文献[3]关于一阶余项R1(t)与n阶余项Rn(t)(n≥2)之间的关系讨论知：假若n阶余项(n≥2)紧(或弱紧)，则可知迁移算子Ak的谱分析及迁移方程解的渐近行态。而假若一阶余项R1(t)紧(或弱紧)，则结论更为精确，条件更弱且得出了半群之间的本质谱关系。

本文通过构造算子，运用比较算子方法，在文献[1，2]的基础上，讨论了具周期边界条件的奇异迁移方程，推广了文[1，2]的结论：即证明了一阶余项R1(t)的弱紧性，从而可得出：半群V(t)与U(t)具有相同的本质谱及一致的本质谱型及迁移方程解的渐近行为等结果。

2 准备知识

令X=L1(△)(△=[-a,a]×E×[-1,1])表相域△上有界可测函数全体按范数

构成的Banach空间，定义△的飞入和飞出的边界分别为：

引入边界空间和范数分别为：

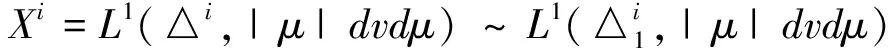
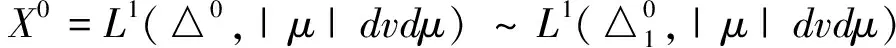
(3)

(4)

其中，～表示这些空间的自然恒等，部分反射边界条件(2)可写成：

(5)

其中

(6)

(7)

显然，H是可逆的，且‖HU‖Χ0=‖U‖Χi，令

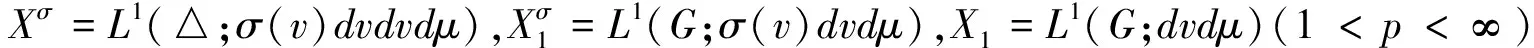
(8)

(9)

则奇异迁移算子Ak定义为

Ak=B+K,D(Ak)=D(B)

(10)

(11)

对φ∈X，考虑方程

(λ-B)φ=ψ

(12)

则对任何Re>-σ0，方程(12)可形式地解为：

(13)

特别地

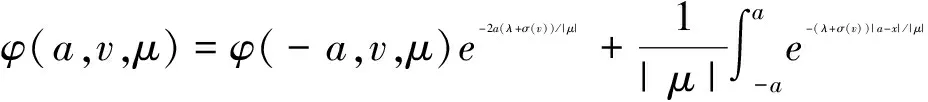
(14)

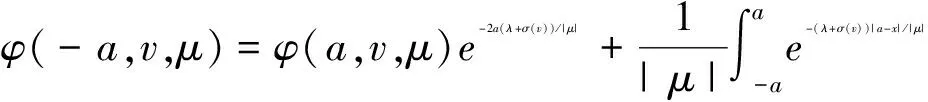
(15)

由(13)-(15)和边界条件(5),则(13)可写成以下抽象形式

(16)

令

(17)

(18)

则对Re>-σ0,有

(λ-B)-1=Ξλ+Mλ

(19)

因为当Reλ>-σ0时，算子Ξλ和Mλ在X上都是正的，所以(λ-B)-1在X上也是正的，且由文献[4]知：∀ψ∈X，B产生一个正C0半群：U(t)(t≥0):

(20)

其中ψ∈X，令

zn(t)φ(x,v,μ)=e-σ(v)tχ[(sgn(μ)x+(2n-1)a)/|μ|,(sgn(μ)x+(2n+1)a)/|μ|](t)

(21)

Zn(t)φ(x,v,μ)=φ(sgn(μ)2na+x-μt,v,μ)zn(t)

(22)

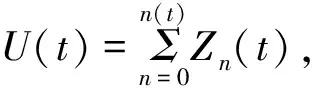
3 主要定理

本节主要讨论奇异算子Ak相应的半群V(t)的Dyson-Phillips展开式一阶余项的弱紧性。

为研究表活剂的界面张力对开发效果的影响，保证模型中其他参数设置不变，改变表面活性剂浓度，使表面活性剂界面张力分别为0.01、0.006、0.003、0.001、0.0005mN·m-1，对比不同界面张力的开发效果，模拟结果见表2。

定理3.1 若假设(O1)、(O2)成立，则R1(t)弱紧。

证明由文献[8,定理2.6]知U1(t)与R1(t)具有相同的紧性。故下面仅证明：

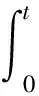
为紧算子。定义

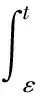
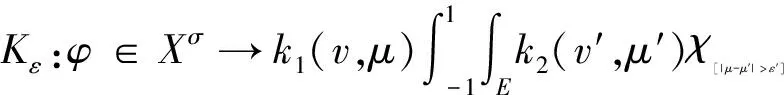
有

定义

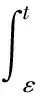
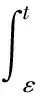
下证F1,n,m紧，令

In,∞(t):L1[R×E×(-1,1)]→L1[R×E×(-1,1)]

φ→e-σ(v)tφ(sgn(μ)2na+x-μt,v,μ)

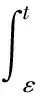
其中

E:X→L1[R×E×(-1,1)]

R:L1[R×E×(-1,1)]→X

于是有

F1,n,m≤Jt

Kε′:L1[R×E×(-1,1),σ(v)dxdvdμ]→L1[R×E×(-1,1)]

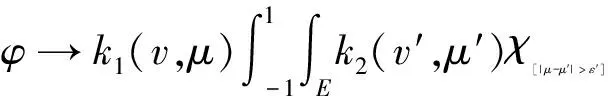
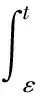
于是有

利用Fubini定理知

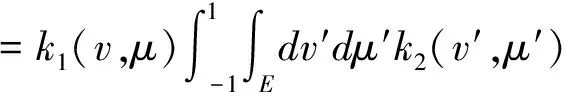
(24)

×φ(x+s(μ-μ′)-μt+sgn(μ)2na+sgn(μ′,2ma),v′,μ′)

作变换，定义

y=y(s)=x+s(μ-μ′)-μt+sgn(μ)2na+sgn(μ′)2ma

于是有

(25)

其中

at(x,μ,μ′)=min{y(ε),y(t)},bt(x,μ,μ′)=max{y(ε),y(t)}

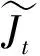
其中

an,m(t)(t)=[(2m+2n)a+a]+3t

定义

F:L1[R×E×(-1,1)]→L1[-an,m(t)(t),an,m(t)(t)×E×(-1,1)]

Et=L1[-an,m(t)(t),an,m(t)(t)×E×(-1,1)]→X

于是有

参考文献：

[1] M.Chabi.K.Latrach.On singular mono-energetic transport equations in slab geomtry.Math.Meth.Appl.Sci.2002,25:1121-1147.

[2] 王胜华,马江山.板几何中一类具周期边界条件的奇异迁移方程. 南昌大学学报.2005,4(29):313-320.

[3] M.sbihi.A resolvent approach to the stability of essential and critical spectral of perturbed.-semigroups on Hilbert spaces with applications to transport-theory.J.Evol.Equ.2007,7:35-58.

[4] K.Latrch and H.Megdiche. Time asymptotic behavior for Retenberg's model with maxwell boundaryconditions. Discrete and Continuous.Dynamical systems.2011,29:305-320.

[5] 王胜华.翁云芳和阳名珠.人体细胞增生中一类迁移算子的谱分析. 数学物理学报.2010,30A(4):1055-1061.

[6] 王胜华.程国飞.一类增生扩散型种群细胞中迁移方程的谱问题. 数学物理学报.2013,33A(1):71-77.

[7] Dodds.P. Fremlin.D.H.Compact operators in Banach lattices.Isr.J.Math.1979,34:287-320.

[8] M.Mokhtar-Kharroubi.Optimal Spectral theory of the linear Boltzmann equation.J.Funct.Anal.2005,226:21-47.

[9] 熊晟欣.高职数学教学中的数学文化渗透探讨[J].职教论坛，2013，(20)：35-36.