航空光电平台机动目标跟踪定位技术应用

刘 烜，胡倩影

（海军装备部航订部，北京100841）

0 引言

随着航空光电平台的广泛应用，利用航空光电平台对机动目标进行实时侦察跟踪定位，获取目标位置及目标运动信息得到了各行业极大的关注。目前，在军事领域利用航空光电平台进行目标探测、目标指示等，在民用领域进行海面监控、海面搜救等方面。但是由于实飞过程中航空光电平台和机动目标均处于运动状态，且平台运动速度远远大于机动目标的运动速度，对目标的跟踪定位与航空光电平台的姿态和动目标的运动状态均有关，目标系统几何校正精度存在一定的误差，上述原因导致目标位置呈离散分布现象，无法正常解算目标的航向航速，所以在复杂的运动环境下实现对机动目标的跟踪，提高目标定位及目标航向航速的精度就显得尤为重要。为解决该问题，在计算目标航向航速前，利用卡尔曼滤波算法对目标位置进行滤波，提高对动目标的测量定位精度，均衡定位误差，解决目标定位发散问题。并通过滑动加权方法进行目标航向解算，通过滑动平均方法进行目标航速解算，提高目标航向航速的精准度。最后通过实验验证本方法的可行性[1，2]。

1 目标位置滤波

卡尔曼滤波是以最小均方误差作为估计的最佳准则，来寻求一套递推估计的算法。其基本思想是:采用信号与噪声的状态空间模型，利用k时刻的估计值和k+1时刻的观测值来更新对状态变量的估计，求出k+1时刻的估计值[3，5]

1.1 系统建模

①系统矩阵

以机动目标的航迹点位置为例，系统矩阵可建立为四维矩阵，即经度、经度方向上的速度、纬度和纬度方向上的速度，它们分别用和表示，经度方向上的加速度和纬度方向上的加速度分别用ulon（k）和ulat（k）表示。

状态方程为:

则系统方程为:

用标准符号x1、x2、x3和x4分别表示Lon和、Lat和。上式中，A为系统矩阵，W（k）为噪声项，T为对目标的采样周期。

②观测矩阵

观测值只有经度和纬度，即Lon和Lat，分别用z1和z2来表示。它们是由状态值和测量噪声组成的，且测量噪声是相互独立的零均值的白噪声。

测量方程为:

则观测方程为:

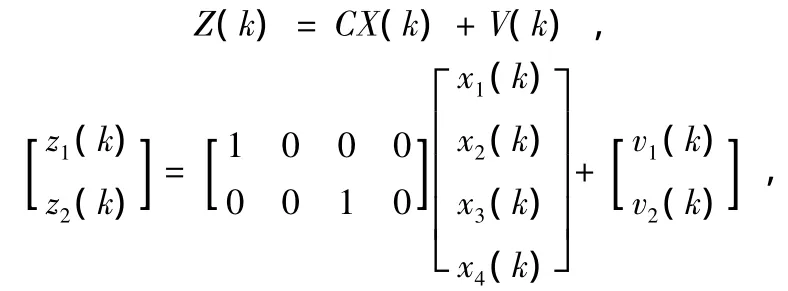
其中，x1（k）=r（k），x3（k）=θ（k）。

③系统噪声协方差矩阵

假定机动目标从k时刻到k+1时刻做匀速运动，但由于大气湍流等因素的影响，目标产生随机加速度，在经度和纬度上都存在随机扰动，于是有:

且

得输入扰动的协方差矩阵:

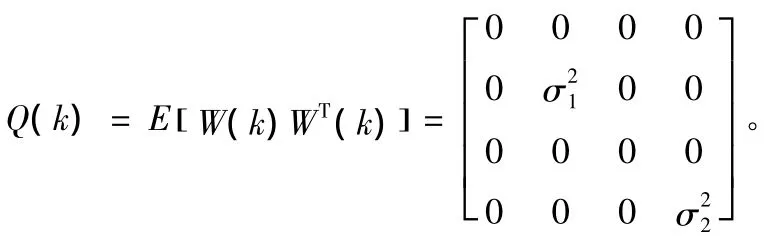
④观测噪声协方差矩阵

在计算滤波器增益时，需要知道观测噪声的协方差矩阵。由于只有两个参数，因此:

用了经度和纬度观测噪声相互独立的条件，故左下角和右上角项为零。

⑤滤波器的初始值

在运算之前，必须对滤波器进行初始化。首先利用一种比较简单的方法确定状态估计值，可利用时刻1和时刻2两点的经度和纬度测量值，即z1（1）、z1（2）、z2（1）和z2（2），建立，而忽略随机加速度。

⑥均方误差矩阵

由滤波器初值，有误差矢量:

从而，

初始误差的协方差矩阵:

由于u和v相互独立，且各噪声采样之间也独立，则:

式中，

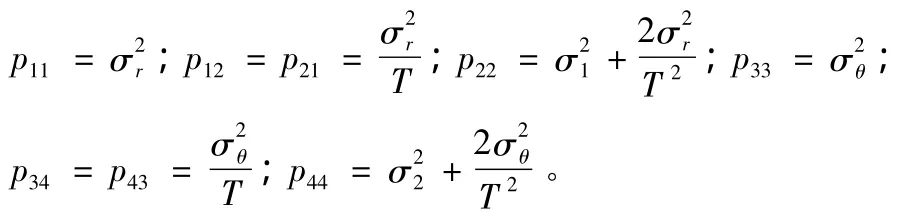
这样，所需要的参数均已具备，可以进行迭代运算了。

1.2 卡尔曼滤波方程组

卡尔曼滤波算法采用递推算法，计算步骤如下:

④由K（k+1）、Z（k+1）和，计算

其中，第③步和第④步计算顺序可交换。

1.3 模型改进

该模型对于状态值为连续的属性项，滤波效果比较稳定。但是对于那些状态值不连续的属性项，比如机动目标航向角，当从360°（0°）连续变换到1°时，虽然对于目标的实际运动状态来说是连续的，但对于滤波数据来说存在跳变，造成滤波效果不理想[6，7]。

为了解决该问题，将角度值进行了三角变换。记机动目标的航向角为θ，在直角坐标系中取单位圆上的点，则该点的横坐标和纵坐标分别为x=rcosθ=cosθ，y=rsinθ=sinθ，x和y均为在[－1，1]区间连续变换的值。因此，对航向角θ的滤波计算转换为对x和y的滤波计算。当计算出x和y的估计值和后，利用，可求得航向角的估计值。当然，该的范围为[－90，90]，若要变换到[0，360]，可根据值和值的正负性，确定所在直角坐标系的象限，若为第一象限，则若为第二或第三象限，则若为第四象限，则

2 航向航速平滑解算

利用目标的大地位置坐标解算目标航向航速，目标的航向C和航速V的计算方法下面详述[8，9]。

2.1 航向计算

通过上述计算方法获取滤波后的目标坐标，由目标相邻两点坐标的连线方向确定目标航向，但由离散点坐标计算的目标航向呈不规则变化，跳动较大，不能真实地反映目标的航向，必须经过平滑处理才能进行分析计算。采用滑动加权方法进行航向平滑，取得较好的平滑效果。

滑动加权的具体方法是对于要计算的第n点的航向Cn，首先通过已知的第n点和第n－1点的位置坐标计算

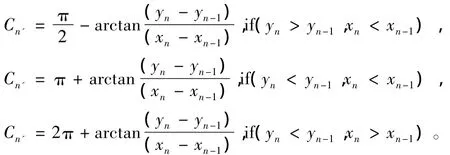
设定滑窗值为l，且已知n点前的l－1个点航向Ci+1，（i=0......l－2），滑窗内l个点对第n点的加权值分别为:，那么第n点的航向为:

2.2 航速计算

对于机动目标，一般来说其运动速度比航空光电平台的运动速度小，为使目标航速逼近真实航速值，采用滑动平均的方法进行计算。具体方法是:假设目标在tk时刻的大地坐标为xk和yk，在tk+1时刻的大地坐标为xk+1和yk+1，设定滑窗值为l，对落入窗体内的l个动目标航迹点，从第1个开始，依次计算第k个与第k+1个值之间的距离，将窗体内的l－1个Vk值求和得，那么第n点的航速

3 定位精度分析

为了验证本文滤波算法对目标定位精度的影响，以及验证计算出的航向航速与真值的偏差，实验在快艇上放置一套高精度GPS定位仪，用于记录快艇的运动航迹及航向航速，通过航空光电平台的遥测数据计算出的快艇位置及航向航速，将其与GPS获取的位置及航向航速真值进行比对[5]。

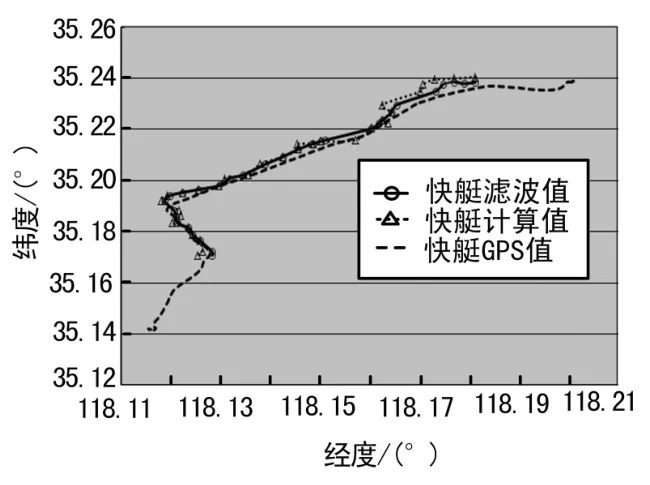
图1 航空光电平台动目标定位精度分析比对结果

其中:目标计算位置点坐标（x2，y2），GPS位置点坐标（x1，y1），按照经度方向1s距离约30m，纬度方向1s距离约27m进行计算，Δdi为测量值与真值间的偏差:

4 结束语

介绍了航空光电平台动目标的跟踪定位算法及在工程中的应用，以及动目标位置滤波算法及动目标航向滑动加权和航速滑动平均算法。在试验中所用数据为光电平台实时拍摄的视频流及相应的平台数据，机动目标搭载GPS定位数据，结果显示目标位置更新频率达到2次/s，滤波后目标定位误差精度达到317.86m（均方根误差），验证了动目标位置滤波算法及动目标运动航向航速算法的可行性。

[1]高峰，冯硕，刘春华.高速几何卡设计与实现[J].无线电工程，2010，40（5）:49－51.

[2]窦兴川，王小东.基于DSP实现舰船目标检测与跟踪[J].无线电工程，2012，42（6）:32－34，38.

[3]李智生，余义德，杜寅峰，等.基于扩展卡尔曼滤波的水下目标测量系统[J].无线电工程，2011，41（4）:53－55.

[4]范洪达，李相民.卡尔曼滤波算法的几何解释[J].火力与指挥控制，2007，27（4）:48－50.

[5]俞卞章.数字信号处理[M].西安:西北工业大学出版社，2002:202－223.

[6]郭玲红，李亚立.基于卡尔曼滤波的动目标运动参数跟踪测量[J].自动化技术与应用，2012，31（8）:20－23.

[7]陈曦，殷华博.基于视觉运动目标跟踪技术分析[J].无线电工程，2011，41（6）:22－24，39.

[8]梁民赞，黄子豪，曹占启.曲线拟合与卡尔曼滤波器的滤波精度评估.无线电工程，2013，43（3）:36－39.

[9]李文静.机动目标跟踪算法[J].无线电工程，2012，42（1）:58－61.

[10]黄孟俊，陈建军，赵宏钟.海上目标航向航速解算新方法[J].信号处理，2011，27（7）:1034－1037.