Ba0．98Bi0．02(Ti0．9Zr0．1)1 －xCoxO3 陶瓷的介电性能及弛豫特性研究

曾卓玮，丁士华，宋天秀，张 倩，钟祥清

(西华大学材料科学与工程学院，四川成都610039)

BaTiO3是最早发现的一种钙钛矿铁电体，其具有优良的性能，在航天、信息科学等领域得到了广泛的应用，BaTiO3基陶瓷材料的制备工艺、尺寸效应等方面的研究也得到了广泛的关注和重视［1-4］。

BaTiO3基陶瓷是一类重要的弛豫铁电体功能材料，掺杂改性是研究其材料性能变化的一种重要方式。有研究表明［5-6］，在 BaTiO3基陶瓷中，Zr4+替代B位Ti4+能有效地降低居里温度，而Bi2O3作为掺杂物可以有效地降低陶瓷烧结温度，增加陶瓷致密度，降低介电损耗;但是，不等价离子的施受主掺杂均会导致晶体内部形成大量缺陷，并且在一定条件下，由掺杂引起的带偶电荷的缺陷将会缔结在一起，形成缺陷团簇，也可被看成是一对缺陷偶极子。在 Eichel et al［7］的研究中，Cu2+易进入 Ti位形成稳定的缺陷偶极子对［Cu″Ti-V··o］，这类缺陷偶极子对与点缺陷 Cu″Ti和 V··O之间的距离相比减小了0.08 nm。BaTiO3陶瓷中缺陷偶极子沿自发极化的方向排列也得到了实验验证［8］。铁电体中偏心杂质离子、补偿电荷以及缔合成的缺陷偶极子均会形成局域无规场。虽然无规场理论［9-11］已经广泛地应用于解释弛豫铁电性，但至今微观存在的缺陷偶极子对宏观介电弛豫的影响依然尚不清楚。

本实验选取Ba(Ti0.9Zr0.1)O3为基础配方，在A、B位分别施受主掺杂2 mol%Bi3+和不同含量的Co3+，讨论通过电荷补偿形式存在的缺陷偶极子对宏观介电弛豫的影响，结合晶体化学特性，分析材料介电性能的变化规律。

1 实验与模拟

1.1 实验方法

实验采用固相反应法制备样品，BaCO3、TiO2、ZrO2、Co2O3、Bi2O3均为分析纯原料，按 Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3(x=0.005，0.01，0.015，0.02)陶瓷的配方进行配料。预烧温度为1 100℃，保温150 min。加入质量分数为8%的聚乙烯醇溶液做黏结剂，造粒后用DY-20型压片机在30 MPa的压强下压成φ10 mm×1 mm的圆片，然后把试样放于烧结炉中升温至1 380℃烧结，升温速度3℃/min，保温时间150 min，随炉冷却。烧结试样经磨光清洗后，涂上银浆，在 810℃烧渗 10 min，采用 Agilent4284A型精密LCR仪器测试实验样品的介电性能，测试温度范围-30～130℃。

1.2 计算模拟方法

本文采用静态原子晶格计算程序Gulp(general utility lattice program)［12］，该计算程序通过采用Mott-Littleton算法简化缺陷周围晶格的方式对晶体结构和性能进行计算模拟。

在基于Born近似条件的计算模拟中，本文采用原子间相互作用势函数的形式如下:

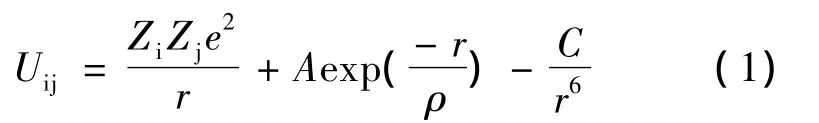
它由传统的长程库仑势和短程Buckingham势组成。式中:r为原子i和j之间的距离;第1项表示库仑势;第2项和第3项共同构成Buckingham势;势参数A、ρ和C分别表示离子的硬度、半径和离子间的范德瓦尔斯力作用强度。

对于晶格中缺陷对周围离子的极化作用，可以采用核壳模型［8］进行处理。基于离子极化率的影响，可以把离子或原子分成核层与壳层，壳层带有电荷Y，核层有质量，带有电荷Z-Y(Z为表观电荷)，通过弹性常数K相互联系作用，因此，因极化作用导致的壳层电子相对位移可表示为

Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷样品计算模拟中所需经验参数如表1、表2所示。

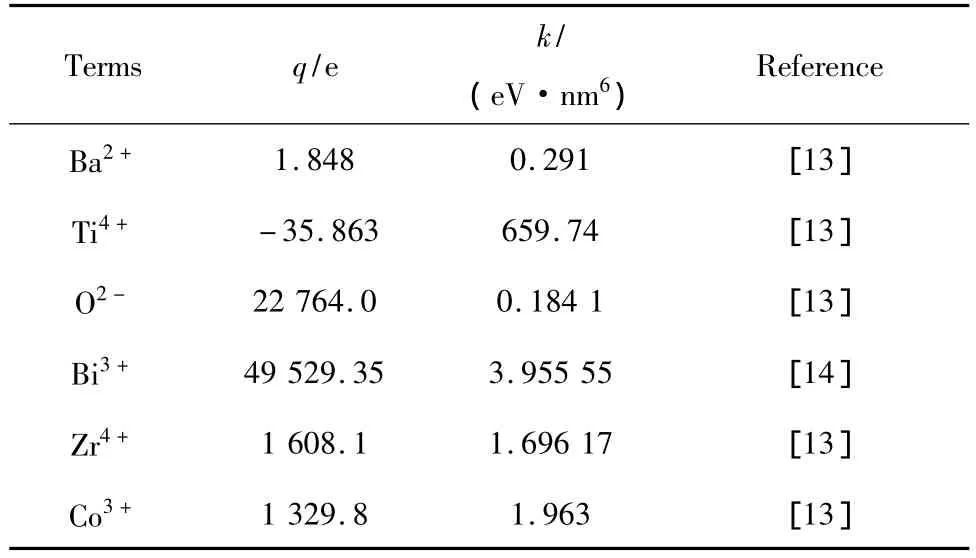
表2 计算模拟所需经验参数

2 结果分析

2.1 XRD分析

图1为室温Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷样品的 XRD谱，结果显示，Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷样品均形成单一四方BaTiO3结构，无明显第二相出现。

图1 Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷样品室温的XRD谱

2.2 介电弛豫特性

图2为Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷在不同频率的介电常数εr与温度t的关系曲线。

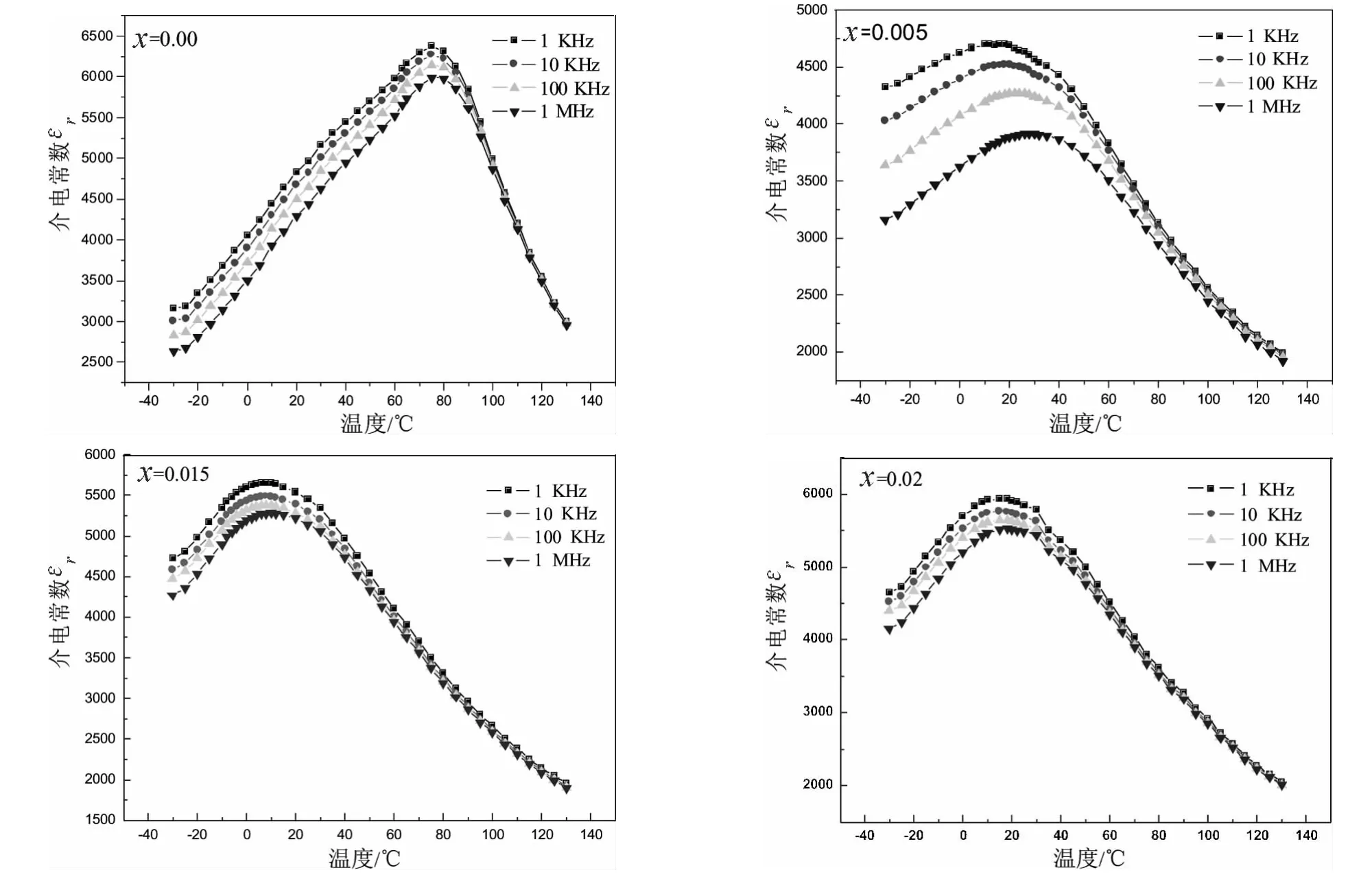
图2 Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷在不同频率的介电常数与温度关系曲线

从图中可以看出:x=0.02样品中，介电峰宽化，但介电峰并没有随着频率的增加向高温方向移动，仅表现出弥散相变铁电体的特征;掺杂量x=0.00，0.005，0.015时，均出现了明显的频率色散和弥散相变特征，表现出弛豫铁电体的特征。

在Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3(0.00，0.005，0.015，0.02)陶瓷的固相反应过程中，Bi3+占据A位替换Ba2+，Co3+将占据B位替换Ti4+/Zr4+，形成的缺陷方程为:

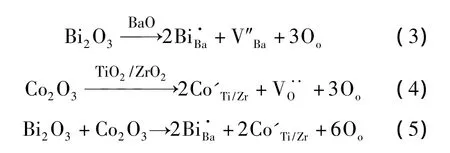
由缺陷方程可知，由于正负电荷容易相互吸引进行电荷补偿，这些缺陷容易缔合成缺陷簇，包括3种:

在铁电体中，无规场的形成将会引起晶格畸变，而体系为了降低能量，将会在晶体内部自发形成极性纳米微区(PNRS)。PNRS的出现是导致弛豫现象的重要原因，PNRS的密度大小也与晶体内部无规场强度有密切联系，而晶体内部缺陷偶极子的存在形式将直接影响晶体内部无规场的强度;因此，晶体内部缺陷偶极子的存在形式和介电弛豫现象有关。

本文通过GULP模拟计算了Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3(x=0.00，0.005，0.015，0.02)陶瓷的各类本征和非本征缺陷能，结果如表3所示。

表3 Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3陶瓷样品的本征缺陷和非本征缺陷能

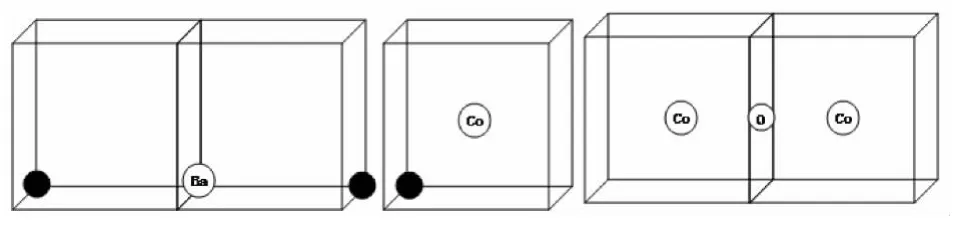
图3 不同缺陷簇在晶体内部最可能的存在形式

通常通过公式(6)表征缺陷簇在晶体内部的稳定性，Ecluster代表缺陷簇能，Eisolated-defect指单一点缺陷能。当计算结果Ebinding为负值时，缺陷簇比孤立点缺陷稳定性更高，在晶体内部易于存在，不易分离。Ebinding分别为 -0.22、-0.58、-1.68 eV。

稳定性从高到低排列分别为［2Co'Ti/Zr-V］、

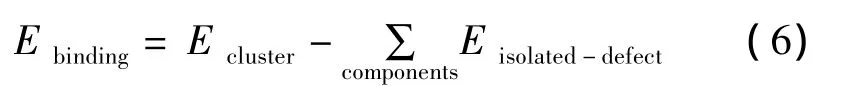
在掺杂量x=0.00、0.01、0.015这3个掺杂溶度下，样品均表现出弛豫铁电体的特征，弛豫程度逐渐降低。根据缺陷簇稳定性的高低排列，在未掺杂Co2O3时，晶体内部只有由杂质Bi3+掺杂引起的缺陷簇 ［2Bi-V″Ba］，补偿缺陷 V″Ba溶度最高，因电价补偿和缺陷偶极子引起的无规场能力最强，PNRS密度最高，对晶体内部长程有序破坏程度最大，因此弛豫程度最强;随着Co3+离子进入晶格，稳定性更高的［Bi-Co'Ti/Zr］将会逐渐形成，随着掺杂溶度逐渐增强，杂质离子分别进入A、B位引入的缺陷电荷相互补偿，此时V″Ba溶度逐渐减小，无规场能力逐渐减弱，弛豫程度逐渐减弱;当掺杂溶度x=0.02时，在测试频率下，介电峰仅表现出强烈的弥散性，未观察到弛豫性，根据电中性条件，由方程(5)可以看出当B∶Co'Ti/Zr=1∶1 时，杂质离子进入晶体形成的缺陷电荷达到平衡条件，即在 x=0.02时，Ba0.98Bi0.02(Ti0.9Zr0.1)0.98Co0.02O3因施受主掺杂引入的缺陷电荷相互补偿，与外来离子所引入的电荷补偿缺陷V″Ba溶度最小，无规场能力最弱，晶体内部长程有序程度最强，所以在测试频率下未观察到弛豫性;在掺杂溶度大于0.02时，晶体内部将会以［2Co'Ti/Zr-V］为主，V溶度随着掺杂量应该逐渐增大，预测样品弛豫程度将逐渐增强。

2.3 结晶化学参数

四方BaTiO3晶体属于钙钛矿型晶体结构，与立方BaTiO3结构相比，晶格常数c变大，a=b变小。根据XRD衍射结果，去对应晶面指数(h、l、k)的角度值，根据最小二乘法原理计算的样品晶格常数以及B位离子的键长如表4所示。

表4 Ba0.98Bi0.02(Ti0.9Zr0.1)O3陶瓷结构参数

键价理论［15］在固态化学领域得到了广泛的应用，对于 Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3(0.00，0.005，0.015，0.02)陶瓷，其 B位离子键价和的计算方法如下:

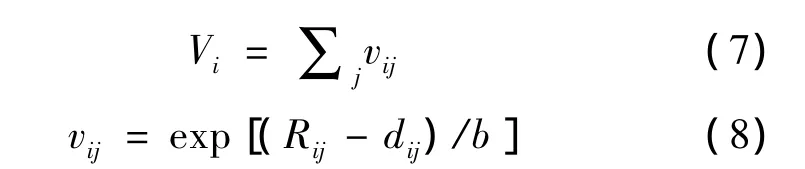
图4为陶瓷样品B位离子键价和与样品1 MHz峰值温度下介电常数以及掺杂量的关系曲线，可以看出:1)随掺杂量的增大，B位离子键价和总体呈减小趋势，但在 x=0.005处发生突变，这是因为Co3+、Ti4+、Zr4+的电负性分别是 1.88、1.54、1.33，表明Co—O键共价成分高于 Ti/Zr—O，Co—O共价键电子云相互作用强于Ti/Zr—O，其次Co3+替代B位使得B位离子之间6s2孤立电子的相互作用增强，从而使得样品晶格常数减小，键价和增大，介电常数减小;2)随着Co3+掺杂溶度增加，键价和逐渐减小，BO6八面体活动性增强，介电常数逐渐增大，在x=0.02处键价和达到极小值，杂质溶度∶Co'Ti/Zr=1∶1，杂质离子进入晶体形成的缺陷电荷达到平衡条件，晶体内部V″Ba溶度最小，B位离子键价和介电常数总体呈反比例关系。

图4 陶瓷样品B位离子键价和与样品1 MHZ峰值温度下介电常数以及掺杂量的关系

3 结论

1)在 Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3(0.00，0.005，0.015，0.02)陶瓷样品中，x=0.00、0.005时，陶瓷样品均体现出强烈的弛豫性，x=0.015处有轻微的弛豫现象，当掺杂量x=0.02时，陶瓷样品仅体现出弥散相变铁电体特征。

2)随着Co3+掺杂溶度的增加，Ba0.98Bi0.02(Ti0.9Zr0.1)1-xCoxO3(0.00，0.005，0.015，0.02)陶瓷内部缺陷偶极子存在形式发生改变，依次为［2B-V″Ba］、［B-Co'Ti/Zr］，x=0.02 时，陶瓷仅体现出弥散相变铁电体特性。

3)结合结晶化学特性，发现随着掺杂量的增加，B位离子键价和与介电常数呈反比例关系，介电常数总体增大。

［1］Lines M E，Glass A M.Principles and Application of Ferroelectrics and Related Materials［M］.Oxford:Oxford Uni Press，1977:24l-250.

［2］涂伟，丁士华，宋天秀，等.包覆MgO对BaTiO3基陶瓷性能的影响［J］.西华大学学报:自然科学版，2012，31(3):77-80.

［3］Luan W ling，Gao Lian，Guo Jingkun.Size Effect on Dielectric Properties of Fine-grained BaTiO3Ceramics［J］.Ceramics International，1999，25:727-729.

［4］Wang Hong，Du Huiling，Yao Xi.Structure Study of Bi2O3-ZnO-Nb2O5based Pyrochlores［J］.Materials Science and Engineering，2003，B99:20-24.

［5］Hennings D，Schnell A，Simon G.Diffuse Ferroelectric Phase Transition in Ba(Ti1·yZry)O3Ceramics［J］.Am Ceramic Soc，1982，65(11):539-544.

［6］Ke S M，Fan H Q，Huang H T，et al.Lorentz–type relationship of the temperature dependence dielectric permittivity in ferroelectrics with diffuse phase transition［J］.Appl Phys，2008，104:034108(1)-034108(7).

［7］Eichel R A，Erhart P，Traskenlin P，et al.Defect-Dipole Formation in Copper-Doped PbTiO3 Ferroelectrics［J］.Phys Rev Lett，2008，100:095504(1)-095504(4).

［8］Warren W L，Dimos D，Pike G E，et al.Defect-dipole Alignment and Tetragonal Strain in Ferroelectrics［J］.Appl Phys Rev Lett，1995，67:1689-1691.

［9］Westphal V，Kleemann W，Glinchuk M D.Diffuse Phase Transitions and Random-field-induced Domain States of the“Relaxor”Ferroelectric PbMg1/3Nb2/3O3［J］.Physics Review Letters，1992，68(6):847–850.

［10］Kleeman W，Klossner A.Glassy and Domain States in Random Dipolar Systems［J］.Ferroelectrics，1993，150(1):35 – 45.

［11］Kleemann W.Random-field induced antiferromagnetic ferroelectric and structural domain states［J］.International Journal of Modern Physics B，1993，7(13):2469–2507.

［12］Gale J D.GULP:A computer program for the symmetry-adapted simulation of solids［J］.J Chem Soc Faraday Trans，1997，93:629-637.

［13］Lewis G V，Catlow C R A.Defect Studies of Doped and Undoped Barium Titanate Using Computer Simulation Techniques［J］.Phys Chem Solids，1986，47:89–97.

［14］Pirovano C，Islam M S，Vannier R N，et al.Modeling the Crystal Structures of Aurivillius Phases［J］.Solid State Ionics，2001，140:115-123.

［15］Brown I D，Shannon R D.Bond-valence Parameters Obtained from a Systematic Analysis of the Inorganic Crystal Structure Database［J］.Acta Cryst，1973，A29:266-282.