四分之一车辆悬架系统振动特性研究
闫宏伟,彭万万,陆辉山,高 强
(中北大学 机械与动力工程学院,太原 030051)
四分之一车辆悬架系统振动特性研究
闫宏伟,彭万万,陆辉山,高 强
(中北大学 机械与动力工程学院,太原 030051)
0 引言
目前,二自由度汽车悬架模型研究方法很多,包括对二自由度悬架模型的频域响应特性研究,不同车速和路面情况下二自由度车辆模型的动力学仿真研究,二自由度汽车车轮动载荷的均方值研究等[1~3]。即用一些理想化的假设将汽车简化成由一系列弹性元件组成的振动系统线性模型,推导微分方程,求解系统响应[4~7]。本文采用理论推导和计算机仿真验证的方法对二自由度悬架模型进行了研究,仿真结果和理论推导完全契合,给出了提高汽车行驶平顺性及安全性的有效措施。
1 整车模型的简化
当一个实际振动系统较复杂时,建立的模型越复杂越接近实际情况,也越能进行逼真的模拟,但往往使分析困难;建立的模型越简单,分析越容易,但得到的结果可能不精确。因此在建立振动系统力学模型时,总是在求得简化表达和逼真模拟二者之间的折中[8]。图1为整车七自由度模型,包括垂直、俯仰、侧倾3个自由度和4个车轮质量的4个垂直自由度。
其中,m1为簧下质量(由车轮和车轴构成),m2为簧上质量[9](由车身、车架、及其上的零部件总成组成),通过减振器和悬架弹簧与车轴、车轮相连接。当质心位置到前后悬架的距离乘积等于或接近于车身绕y轴的回转半径的平方时,则前后悬架系统的垂直振动几乎是独立的,此时可将汽车振动系统进一步简化为车身和车轮二自由度振动系统模型,如图2所示。

图1 整车七自由度模型

图2 单轮双质量二自由度模型
2 双质量振动系统数学模型
2.1 双质量系统振动微分方程
双质量系统振动模型不仅可以反映车身部分的动态特性,还能反映车轮部分在10Hz~15Hz范
围产生高频共振时的动态特性[10]。设车轮与车身垂直位移坐标为z1、z2,坐标原点选在各自的平衡位置,对上述单轮双质量二自由度模型列写微分方程:
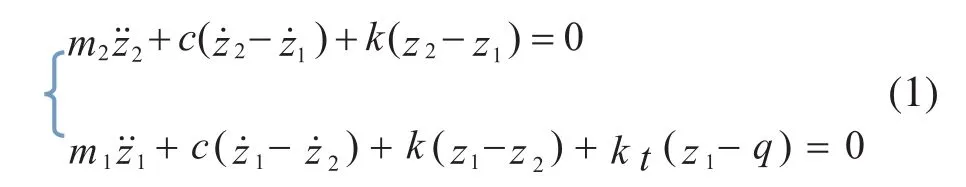
式中,m2为悬挂质量(簧上质量,包括车身等);m1为非悬挂质量(簧下质量,包括车轮、车轴等);k、kt分别为悬挂和轮胎刚度;c为悬挂阻尼系数。
2.2 主频率及主振型的理论推导
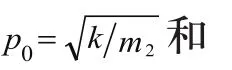
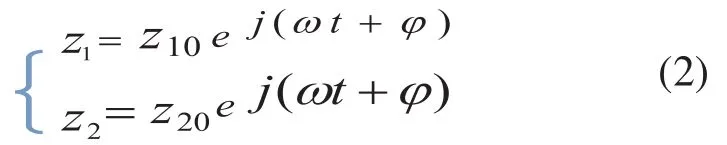
将上面方程组代入(1),另阻尼c为零,并将p0和pt代入化简,得:
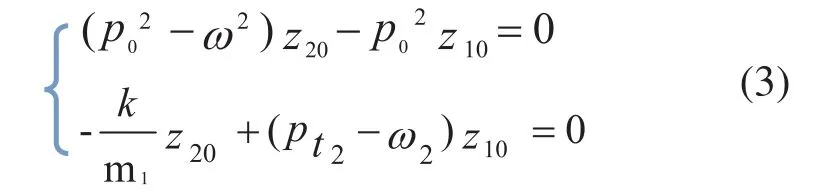
方程组(3)的两个根即为二自由度系统的两个主频率ω1和ω2的平方。由此可得系统的一阶主振型和二阶主振型,即:
一阶主振型:

3 算例分析
3.1 算例主振型的解算
设某汽车车身固有圆频率为p0,质量比rm=m2/m1=10,刚度比rk=kt/k=9,则可分别求出系统的主频率和主振型,即:
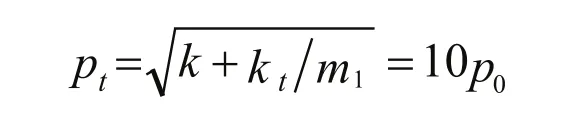
系统两个主频率分别为:

由此可见,低的主频率ω1与车身固有圆频率p0接近,高的主频率ω2与车轮固有圆频率pt接近,且有ω1 在强迫振动情况下,激振频率ω接近系统主频率ω1时将产生低频共振,按一阶主振型振动,车身的振幅比车轮的振幅大将近10倍,所以主要是车身在振动,称为车身型振动;当激振频率ω接近系统主频率ω2时,产生高频共振,按二阶主振型振动,此时车轮的振幅比车身的振幅大将近100倍,称为车轮型振动[11]。 本例中运用AMESim建立四分之一车体的二自由度振动模型,验证上述结论的正确性。AMESim作为多学科领域复杂系统建模仿真平台,用户可以在这个单一平台上建立复杂的系统模型,并在此基础上进行仿真计算和深入分析,也可以在这个平台上研究任何元件或系统的稳态和动态性能。在其机械库和信号库中选择相应元件,建立如图3所示模型。 图3 单轮双质量二自由度AMESim模型 按上述质量比rm和弹簧刚度比rk设置参数后,把车身速度和轮胎速度设为观测变量,运行10s的线性化仿真(时间间隔为0.1s),得到该系统在低频和高频时的模态振型和速度曲线图。 图4 低频时模态振型及速度曲线 图5 高频时模态振型及速度曲线 在低频(1.08Hz)时,车身的模态振型明显增大(车身振幅约为车轮振幅的10倍),其速度也表现出明显的震荡,而在高频(12.73Hz)时正好相反,与前面的结论相吻合。 当把两弹簧中产生的力设为观测变量时,可得到低频和高频时的弹簧力随时间变化的规律。 图6 低频时弹簧力曲线 图7 高频时弹簧力曲线 在低频(1.08Hz)阶段,悬架弹簧和轮胎刚度弹簧力变化趋势相同且大小相近,两弹簧相当于串联。在高频(12.73Hz)阶段,两弹簧力变化趋势近似相反且弹簧力成一定比例,相当于两弹簧并联。此时车轮固有圆频率pt和阻尼比ςt表达式分别为: 对于二自由度系统的车轮型振动模型,由于车身部分振幅很小,由式(6)、式(7)可知, 降低轮胎刚度能使车轮固有圆频率下降,使簧下质量系统的阻尼比加大,从而减小车轮部分高频共振时的加速度。降低非悬挂质量可使车轮部分动载下降,有利于提高车辆的行驶安全性。 AMESim仿真平台在车辆悬架建模仿真中能够获得良好效果,它对系统简化、线性化处理及结果可视化有很大帮助。 [1]詹长书,吕文超.汽车悬架的二自由度建模方法及分析[J].拖拉机与农用运输车,2010,37(6):9-15. [2]李俊,张维强,袁俊.基于Matlab的二自由度车辆的动力学仿真[J].科学技术与工程,2010(4). [3]郑昭明.二自由度汽车车轮动载荷的均方值计算公式[J].武汉交通科技大学学报,1996(1). [4]王岩松,何辉,耿艾莉.车辆-人体系统振动时域模拟及悬架非线性分析[J].振动与冲击,2007,12(26):36-39. [5]Sheng X,Thopson D J.Simulation of Roughness Initiation and Growth on Railway Rails[J].Journal of Sound and Vibration,2006,(293):819-829. [6]黄采伦.列车故障在线诊断技术及应用[M].北京:国防工业出版社,2006. [7]岳建海,裘正定.基于连续子波变换的铁路车轮踏面擦伤的在线检测[J].铁道学报,2003,4(25):27-30. [8]周长城.车辆悬架设计及理论[M].北京:北京大学出版社,2011. [9]彭莫,刁增祥,党潇正.汽车悬架构建的设计计算[M].北京:机械工业出版设,2012. [10]马国清,檀润华.油气悬挂系统非线性数学模型的建立及其计算机仿真[J].机械工程学报,2002,38(5):95-99. [11]何渝生.汽车振动学[M].北京:人民交通出版社,1990. The vibration character analysis of quarter-car suspension system YAN Hong-wei, PENG Wan-wan, LU Hui-shan, GAO Qiang 建立了汽车双质量二自由度线性化振动模型,推导出无阻尼自由振动时二自由度系统主振型的表达式,分析了在不同频率下车身和车轮的振动特性,得出在低频和高频激振力下,车身振幅和车轮振幅分别对系统的振动起主导作用,并基于AMESim对该系统进行仿真,验证了结论的可靠性,提出了提高车辆行驶安全性的措施,为系统的设计汽车悬架奠定了研究基础。 悬架;二自由度模型;主振型;振动特性;AMESim 闫宏伟(1969 -),男,山西太原人,博士,研究方向为智能设计与监测技术。 U469.3 A 1009-0134(2014)06(上)-0089-03 10.3969/j.issn.1009-0134.2014.06(上).26 2014-03-16 山西省自然科学基金项目(2013011026-2);国家自然科学基金资助项目(50775154)
3.2 双质量车身车轮振动的AMESim模型

4 仿真结果
4.1 模态振型与激振频率的关系


4.2 弹簧刚度与激振频率的关系



5 结论

