一种有效的面向高维数值型数据的聚类方法
李顺勇,宋云胜,赵兴旺
(1.山西大学 计算机与信息技术学院,山西 太原 030006;2.山西大学 数学科学学院,山西 太原 030006)
0 引言
聚类作为数据挖掘中的一项重要技术,人们利用对数据的分析从中发掘有用的信息。作为一种无监督的学习方法,聚类从数学分析的角度提供了一种对数据进行准确、细致的分析工具。对一个给定的数据(对象、记录)集,聚类或划分的目的就是把这些对象归到相应的组或“簇”中,使得类内(intra-class)数据或对象的相似性最强,以紧致度描述;类间(inter-class)数据或对象的相似性最弱,以分离度描述。聚类质量的高低通常取决于聚类方法所使用的相似性度量方法和实现方式,作为一种无监督的学习方法(unsupervised learning),能够从研究对象的特征数据中挖掘出有用的模式。因此,聚类是一种强有力的信息处理方法。它在数据挖掘、图像分割、模式识别、空间遥感技术、特征提取、信号压缩以及在中医医药等诸多领域中有着广泛的应用,并取得了一些令人满意的效果。
数据挖掘涉及的数据可能包括很多属性,有时可达成百乃至上千、上万。聚类方法在处理这样的高维数据时往往会碰到较大的困难。聚类方法的选择取决于数据的类型和聚类应用的目的。常用的聚类方法有基于划分的、基于层次的、基于密度的、基于网格的以及基于模型的等。而相似性常常是用来计算聚类的有效方法。本文提出了一种针对高维数值型数据进行聚类的有效方法,利用相关数据进行了验证,实验结果证明了其理论和应用的有效性。
UCI Machine Learning Repository中有许多高维数值型数据集,部分数据集见表1。

表1 UCI中的部分数值型数据集Table 1 Parts of the UCI numeric data set
我们以SPECTF Heart为例,该数据集有267个对象,44个属性,分为两类,其数据表示如图1,其中横坐标为维数个数(Dimension(a)),纵坐标为无量纲化的数值(Dimensionless Number),图2类似。
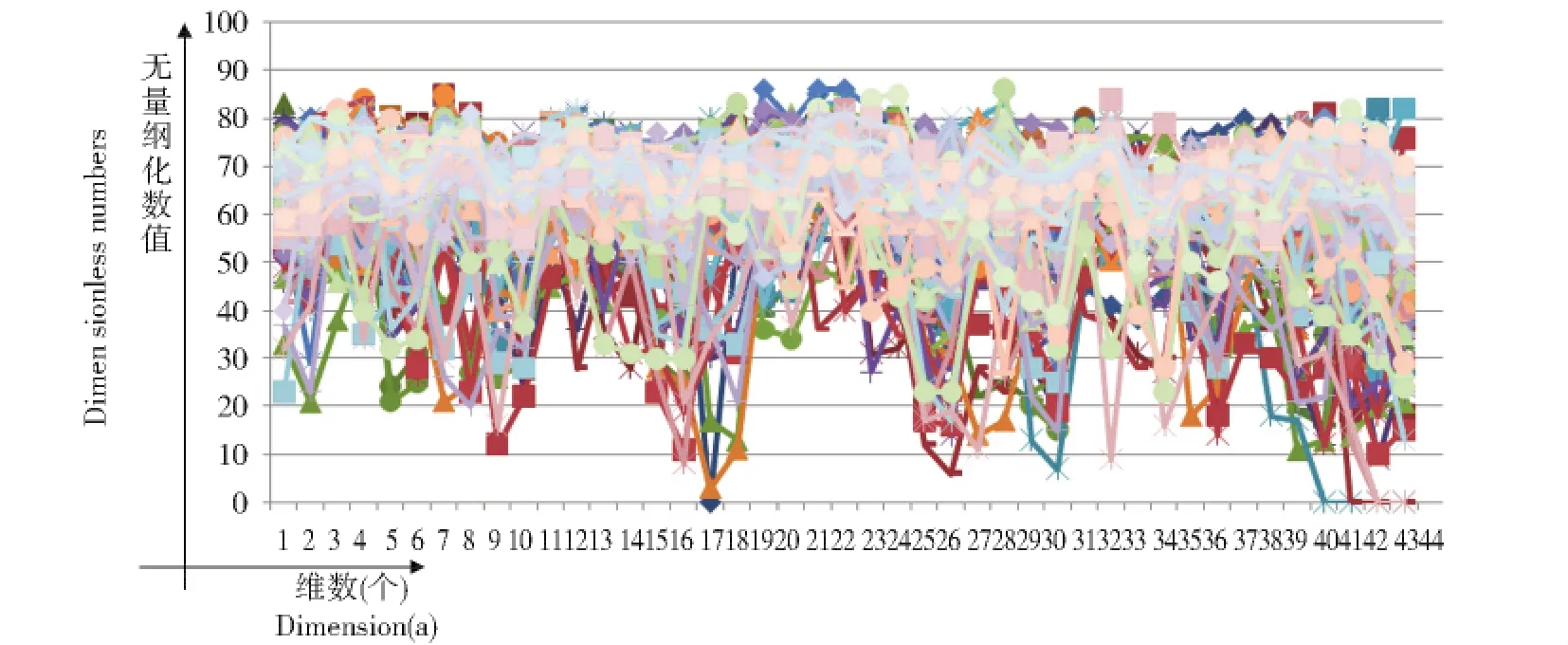
Fig.1 Discrimination of SPECTF Heart data图1 SPECTF Heart数据区分
从图1中我们很难区分它们之间的相似度或类别归属。为了清楚地表示数据之间的区别,以Anseombe数据[1]为例。图2中显示Anseombe数据中的x1,x2,x3以及y的11个属性值都比较接近,较难区分,那么哪个和y更接近(或可归为一类)?

Fig.2 Discrimination of Anseombe data图2 Anseombe数据区分
实际问题当中,有许多这样的数据需要区分或对它们进行归类。一个“好”的方法只有在实际应用中才能体现其优势。
1 三类经典的距离度量方法[2]
设,x=(x1,x2,…,xn),y=(y1,y2,…,yn)为两个向量。
1.1 相关系数(Pearson correlation coefficient)
相关系数通常用来描述两个向量的相关性。

|ρ|值越大,x,y相似性越好。
1.2 瑞利熵(Rênyi entropy)[3]
熵用来度量无序性,熵值越大越好,类的区分度也越好[4],其中α=2,σ=3。

1.3 欧氏距离(Euclidean distance)

dE值越小,x,y相似度越大,dE=0时,表明x,y二者完全一样。
以上三种方法都是经典的计算相似性的方法,各有优劣,还有一些计算相似性的方法见文献[5-9]。利用1.1、1.2、1.3对Anseombe中的数据计算x1,x2,x3和y的相似度,其结果如表2。

表2 经典方法相似度比较Table 2 Similarity comparison of Classical method
表2显示三种经典方法对x1,x2,x3和y的整体相似度区别不大,有的几乎难于区分,但图2显示x1,x2,x3和y还是有区别的。
为了有效地区别x1,x2,x3和y,本文提出了新的线性相似度(Linear Measure)。
2 新的线性相似性度(LM)

3 实验性分析对比
为了检验文中提出方法的有效性,我们重新对表1中的数据进行了相似度计算,结果见表4。

表3 LM-dnew方法Table 3 LM-dnew method
由表3我们明显可以看出x3和y最相似,可以归为一类(组),x2和y次之,x1和y最差。图3为LM-dnew和三种经典方法的比较演示,图3中显示新的线性相似度对该类数据有较好的灵敏度。
在相似性计算和聚类问题上,我们所寻求的方法,一方面希望相似性越精确越好,另一方面,更希望方法越简单越好。
文中提出的方法既然能处理两两数据之间的相似性问题,那么它也就能处理一个数据和一个类之间的问题,同时也就能处理类和类之间的问题,这将会是我们以后研究的新方向。

Fig.3 Comparison of four methods图3 四种方法比较演示
4 结论
本文提出了一种有效的面向高维数值型数据的聚类方法,通过实验比较,结果显示该方法有较好的灵敏度,能对某些高维数值型数据起到较好的聚类效果,值得进一步研究和推广。
[1] Suykens J A K.Nonlinear Modeling and Support Vector Machines[J].IEEEInstrumentationandMeasurementTechnologyConference.Budapest,Hungary,2001:21-23.
[2] 张宇,刘雨东,计钊.向量相似度测度方法[J].声学技术,2009,28(4):532-536.
[3] Renyi A.On Measures of Entropy and Information[C].Proceeding of the 4th Berkeley Symposium on Mathematics of Statistics and Probability,1961:547-561.
[4] Liang Ji-ye,Zhao Xing-wang,Li De-yu,etal.Determining the Number of Clusters Using Information Entropy for Mixed Data[J].PatternRecognition,2012,45:2251-2265.
[5] Jiang Qing-shan,Zhang Yan-ping,Chen Li-fei.An Initilization Method for Subspace Clustering Algorithm[J].IJIntelligentSystemsandApplications,2011,3:54-61.
[6] Christian Borgelt.Accelerating Fuzzy Clustering[J].InformationSciences,2009,179:3985-3997.
[7] Cheng Victor,Li Chun-hung,Kwokb James T,etal.Dissimilarity Learning for Nominal Data[J].PatternRecognition,2004,37:1471-1477.
[8] Rudi L.Cilibrasi and Paul M.B.Vitanyi.The Google Similarity Distance[J].IEEETransactionsonKnowledgeandData Engineering,2007,19(3):370-383.
[9] Nikolaj Tatti.Distances Between Data Sets Based on Summary Statistics[J].JournalofMachineLearningResearch,2007,8:131-154.
[10] Cao Fu-yuan,Liang Ji-ye,Li De-yu,etal.A Dissimilarity Measure for the k-Modes Clustering Algorithm[J].Knowledge-BasedSystems,2012,26:120-127.

