附合水准路线的蚁群智能平差方法

吕彩忠，廖小辉

附合水准路线是工程建设中水准控制测量的一种主要测量路线，在公路工程、土木建筑工程、水利工程、电力工程及变形监测等工程建设项目中广泛使用。附合水准路线测量的精度与工程建设的质量有着密切的关系，因此，对附合水准路线测量的误差处理方法开展研究，具有重要的意义。

为提高附合水准测量的精度，许多学者对附合水准测量的误差处理方法开展了一系列的研究。张琦［1］等人对附合的1条水准路线图解平差方法研究发现，该方法作业步骤简单，且能够满足三、四等水准测量的精度要求。王磊［2］等人通过对间接平差模型的简化，利用Matlab编制了附合水准网经典平差系统，并用假设检验理论检验系统的可靠性，通过实例验证发现，该平差系统可以对一、二、三、四等及等外附合水准网开展经典平差计算。余章蓉［3］等人对水准网间接平差方法进行改进，采用直接观测信息构建方程的方法实现了间接平差，该方法实现程序编制简单、快捷、高效，方便了大型水准网平差计算。

相比之下，水准网平差的人工智能计算方面的研究甚少。吴良才［4］等人把遗传算法和神经网络技术结合在一起，用于GPS高程的转换。通过实例计算，表明人工智能算法用于GPS高程转换的精度较高。

作者拟建立附合水准路线的通用平差模型，研究建立蚁群智能水准平差方法。其目的在于改进平差手段，提高水准平差的精度。

1 平差模型的建立

如图1所示，假定待测点为1，2，…，i，…，j，从BMA到BMB之间设置了n个测段，按照五等水准测量的方法施测，各测段的实测高差分别为h1，h2，…，hn，各测段的距离分别为 L1，L2，…，Ln，设各测段的高差真值分别为h～1，h～2，…，h～n，设各测段的真误差分别为Δ1，Δ2，…，Δn，则

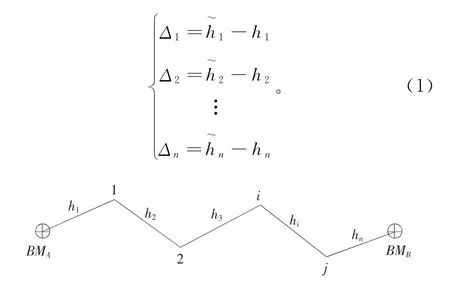
图1 附合水准路线示意Fig.1 The schematic diagram of annexed leveling

显然，该水准路线的必要观测数为n－1，由此可以获得该水准路线的条件平差方程为：

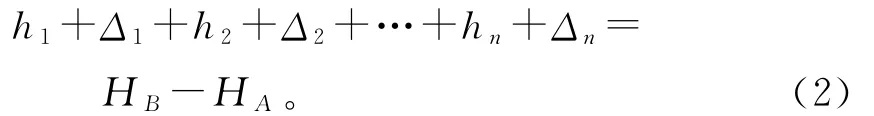
若使用同一套仪器，同样的测量人员对路线进行水准测量，很显然，测段距离越长，测站数也就越多，相应的测量误差也就越大，因此，可以假定第i测段的误差Δi与测段距离成正比关系，即

式中：ki为［0，1］间的参数；Li为第i测段的距离.

可以确定，若Li＜Lj，则Δi＜Δj。

将各测段实测高差按距离排序，整理得：

由于该水准路线采用了等外水准测量，按《工程测量规范（GB50026－2007）》规定，误差的限差为±30，由此，可以得到各测段的误差限差：

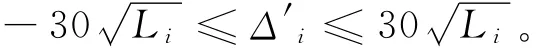
水准路线总的误差限差为：

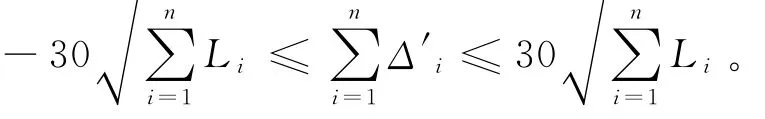
由最小二乘法原理可得到附合水准路线的平差数学模型为：

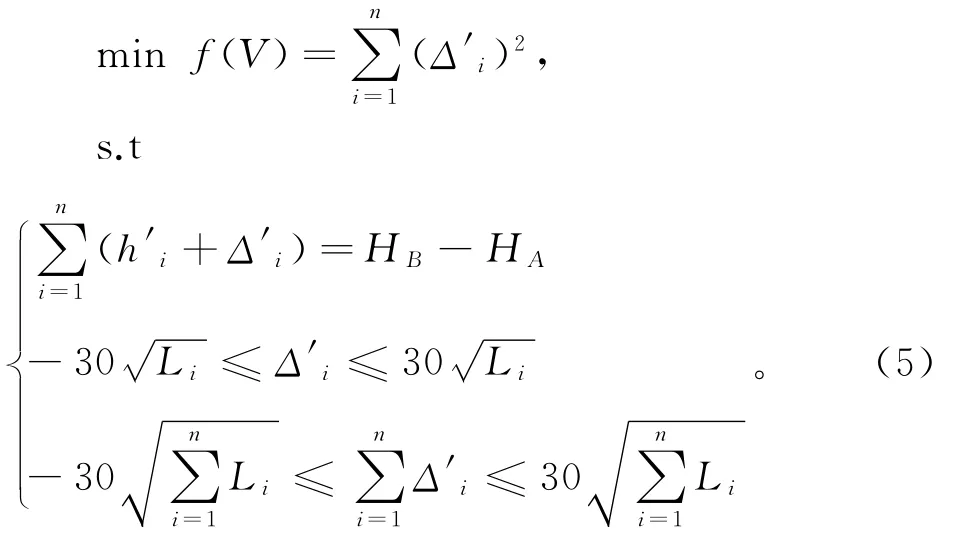
2 附合水准路线平差的蚁群算法

2.1 蚁群算法

20世纪90年代，意大利学者Dorigo［5］等人提出模拟蚁群觅食的蚁群算法。该算法的特点是：拥有强鲁棒性、优良的分布式计算机制，且易与其他优化理论相结合［6－7］。该方法已经被用于解决大多数的优化问题［8］。目前，其应用领域已逐步扩展到工程建设方面。

2.2 蚁群搜索方式设计

蚂蚁i的搜索方向与蚁群中其他蚂蚁的位置的信息素以及距离有密切关系，信息素越大，且与当前蚂蚁i的距离越小，被当前蚂蚁选定为搜索方向的概率也就越大，若蚂蚁i与蚂蚁j的距离为dij，则

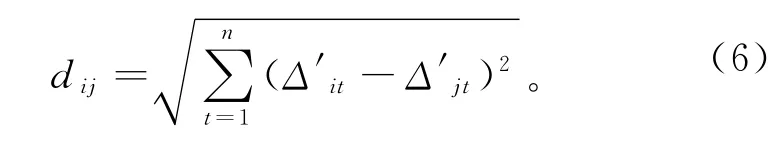
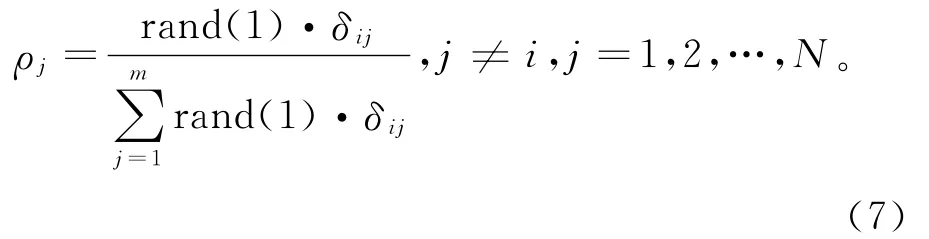
2.3 蚂蚁行进策略设计

确定蚂蚁i向蚂蚁j方向行进后，设计当前蚂蚁i的移动方案为：

1）预先设定蚂蚁的移动范围r。若dij＞r，则蚂蚁i朝蚂蚁j方向移动r距离；相反，蚂蚁i移动到蚂蚁j的位置。

2）对蚂蚁i移动后的位置增加扰动系数φ，即V′i＝Vi·φ＝（Δi1·φ，Δi2·φ，…，Δin·φ）。

2.4 精英保留策略

在蚁群平差优化计算过程中，采用精英保留策略，可以提高平差的进度。具体实现方法为：对每代蚁群搜索的结果，将平差结果的最优值（即fi（V）最小值）提取出来，替换下一代蚁群搜索的解中的最劣解。如此反复，实现在迭代过程中将各代的最劣解淘汰，而各代的最优解被保存到下一代中。

2.5 蚁群算法基本步骤

为求解式（5），设计蚁群算法步骤为：

1）根据式（5）确定的约束条件，随机产生初始蚁群POP，确保蚂蚁初始位置所代表的解为可行解，设蚁群规模为N，计算初始蚁群中蚂蚁个体所在位置的目标函数为fi（V），i＝1，2，…，N，确定和存储当前最优解W0＝minfi（V）。

2）令迭代次数计数值Nc＝0，即蚂蚁开始觅食。

3）令i＝1，即控制对第i只蚂蚁的行进。

4）产生随机数p，p∈［0，1］，对当前蚂蚁i，按式（7）计算蚂蚁i向蚂蚁j方向移动的概率，确定蚂蚁i的行进方向。

5）按蚂蚁行进策略设计的方法移动蚂蚁i，计算蚂蚁i新位置的目标函数fi（V）。

6）i＝i＋1，若i≤N，则跳转到4）；否则，跳转到7）。

7）若当前代的最优解优于原有的最优解，更新W；若原有的最优解优于当前代的最劣解，则用原有的最优解替换当前代的最劣解。

8）令Nc＝Nc＋1，若Nc＜Ncmax，跳转到3）；否则，输出计算结果。

2.6 蚁群算法流程图

基于蚁群算法的附合水准路线平差方法的具体流程如图2所示。

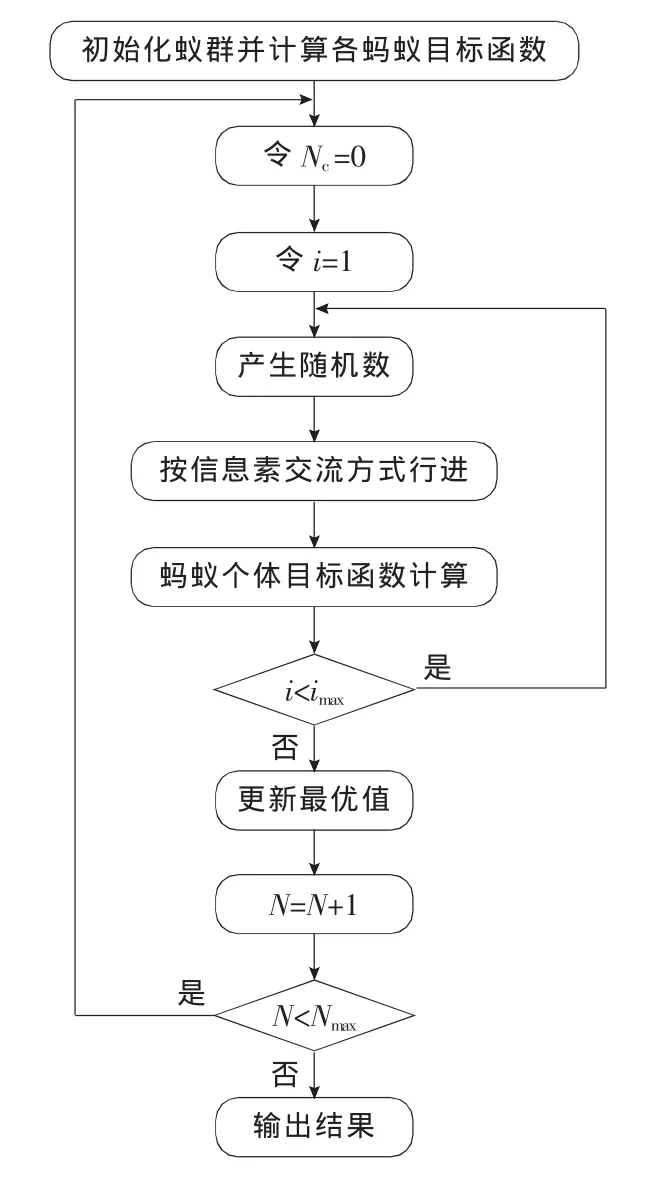
图2 蚁群算法流程Fig.2 The flow chart of ant colony algorithm

3 工程应用

一附合水准路线测量如图3所示，A和B分别为已知高程的水准点；1，2和3分别为待定高程的水准点；h1，h2，h3和h4分别为各测 段 观 测高差；n1，n2，n3和n4分别为各测段测站数；L1，L2，L3和L4分别为各测段长度。现已知HA＝65.376m，HB＝68.623m，各测段站数、长度及高差均注于图3中。

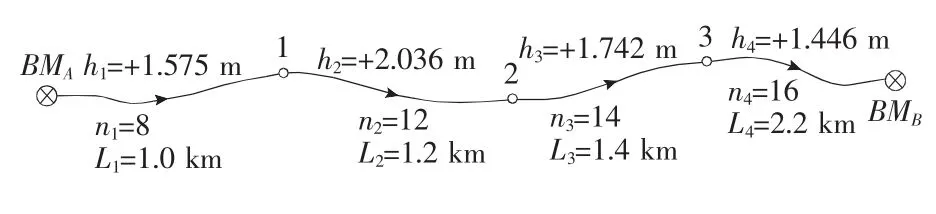
图3 附合水准路线观测示意Fig.3 The survey schematic diagram of annexed leveling

3.1 平差函数的建立

根据式（5）可得平差函数为：

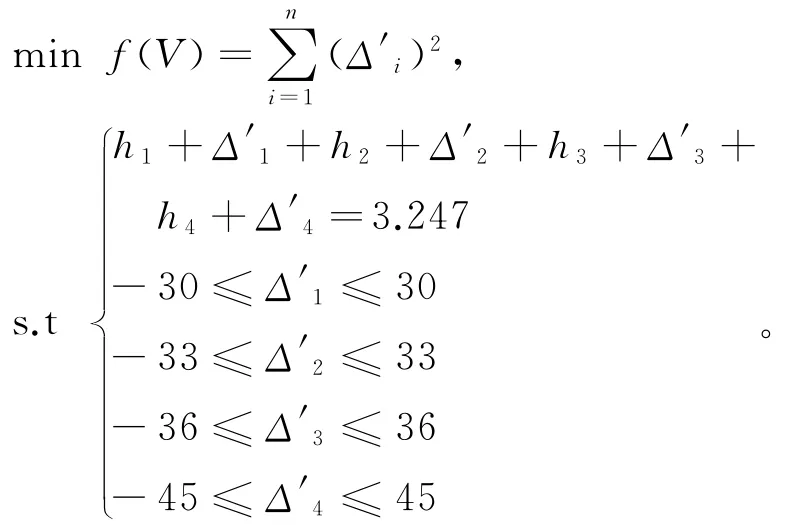
3.2 平差结果

该案例使用Matlab7.0编制蚁群算法计算程序，设置初始蚁群规模为20，随机产生初始种群见表1。设置迭代次数为30次，迭代过程如图4所示。平差的结果为：Δ1＝－16，Δ2＝Δ3＝－17，

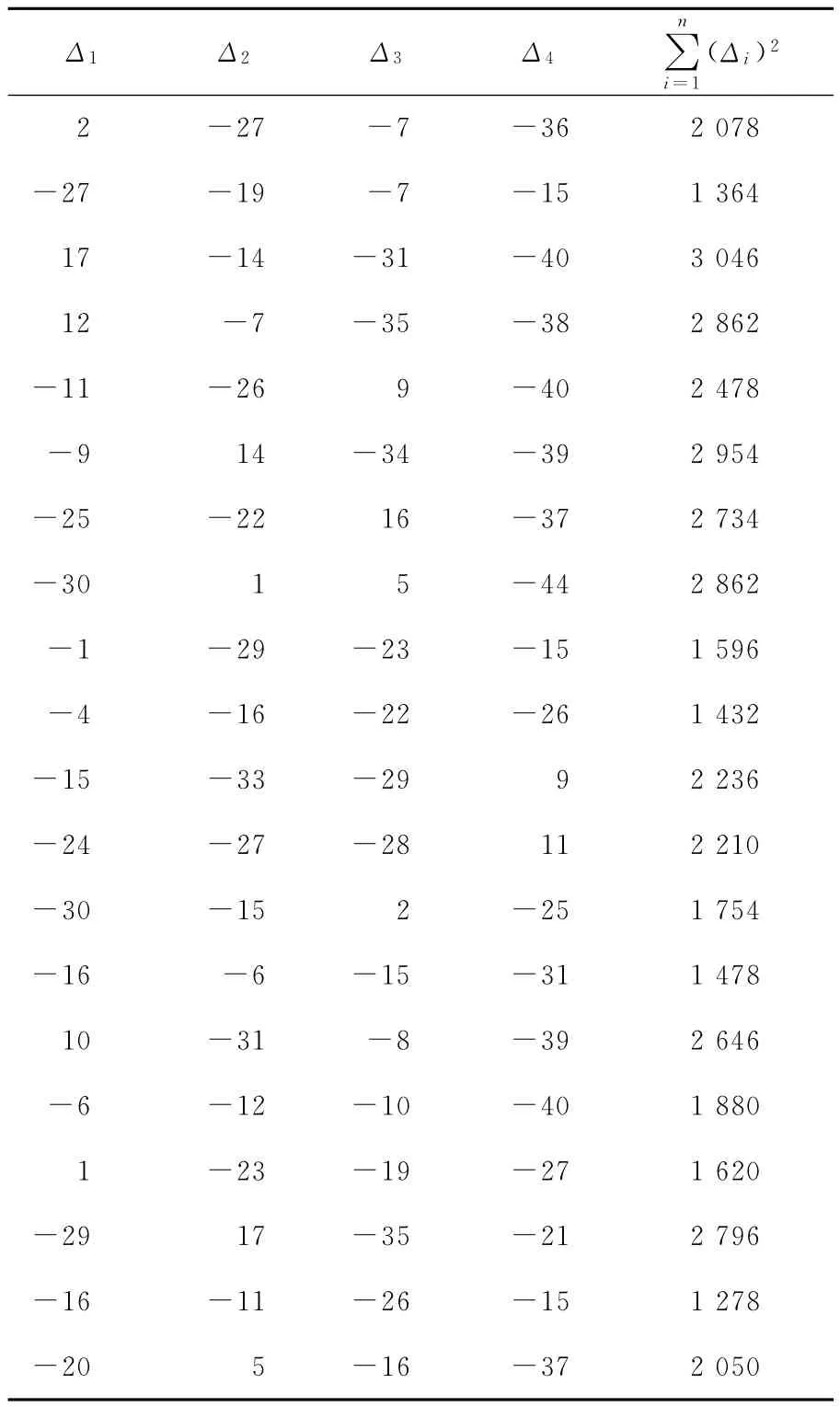
表1 初始蚁群Table 1 The initial ant colony

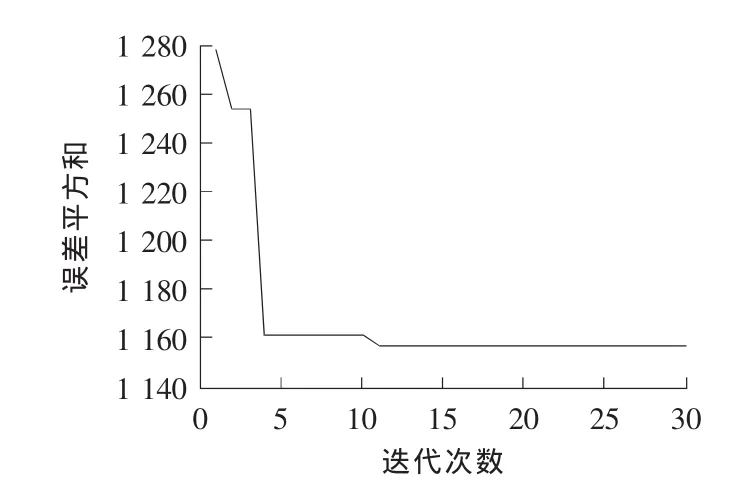
图4 附合水准路线蚁群智能平差法迭代过程Fig.4 The iterative process about adjustment calculation of annexed leveling based on ant colony algorithm

3.3 平差精度分析

假设各测站观测高差是精度相同的独立观测值，其方差为σ2，若按传统平差方法，即按水准路线总测站数或水准路线的总距离平均分配，本例按总测站数平均分配，显然，各测段的中误差分别为：

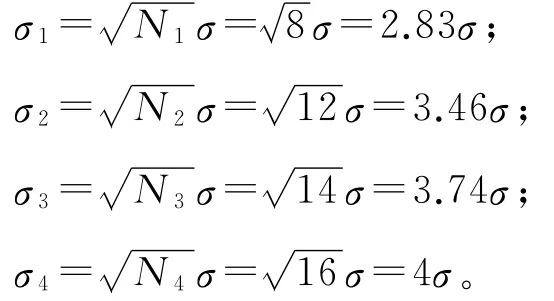
假设该水准路线观测的总误差为Δ总，且误差分配后各测段的高差分别为，则：

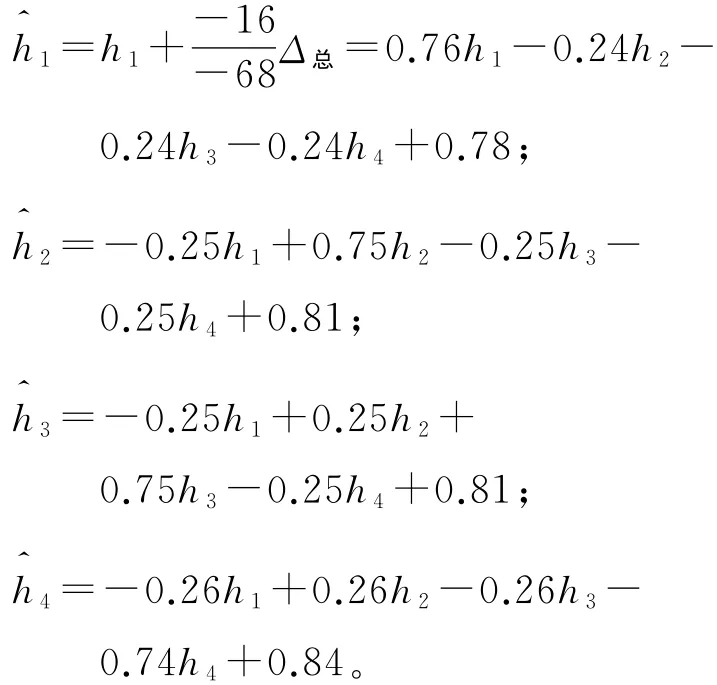
所以，

由此可得：

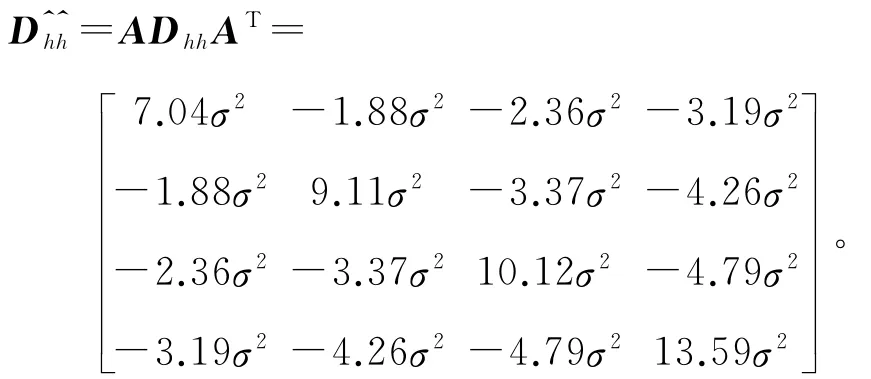
从分析可见，按蚁群算法分配，各测段的中误差为：

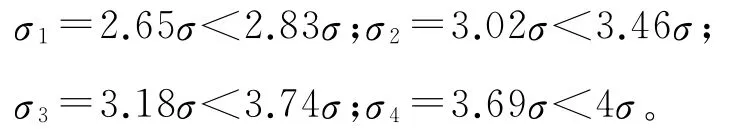
4 结论

1）通过对附合水准路线测量的误差特点分析，建立了附合水准路线的误差处理通用优化模型，便于计算机程序优化计算。

2）提出了附合水准路线的蚁群智能平差方法，建立了附合水准路线平差的蚂蚁搜索方案和蚂蚁的行进策略。采用精英保留策略，实现快速、高精度平差。

3）通过实例计算可以发现，附合水准路线采用蚁群智能平差方法的精度明显高于采用传统经典平差方法的精度。

（

）：

［1］ 张琦，修涛.单一结点或附合的水准路线的精度评定［J］.露天采矿技术，2013（2）：52－56.（ZHANG Qi，XIU Tao.Evaluation of the accuracy of a single node or annexed leveling line［J］.Opencast Mining Technology，2013（2）：52－56.（in Chinese））

［2］ 王磊，谭志祥，张鲜妮，等.基于 MATLAB的水准网经典平差系统的开发和应用［J］.测绘科学.2010，35（9）：223－225.（WANG Lei，TAN Zhi－xiang，ZHANG Xian－ni，et al.Exploiter and application of classical adjustment system of elevation net based on MATLAB［J］.Science of Surveying and Mapping，2010，35（9）：223－225.（in Chinese））

［3］ 余章蓉，王友昆.不构建误差方程系数阵B实现水准网间接平差［J］.城市勘测，2008（2）：75－78.（YU Zhang－rong，WANG You－kun.Don’t build error equation coefficient matrix B level net indirect adjustment［J］.Urban Geotechnical Investigation ＆ Surveying，2008（2）：75－78.（in Chinese））

［4］ 吴良才，危志明.转换GPS高程的遗传神经网络方法［J］.测绘科学技术学报，2007，24（4）：243－246.（WU Liang－cai，WEI Zhi－ming.Conversion of height by genetic neural network method［J］.Journal of Zhengzhou Institute of Surveying and Mapping，2007，24（4）：243－246.（in Chinese））

［5］ Dorigo M.Optimization，learning and natural algorithms［D］.Milano，Italy：Politecnico di Milano，1992.

［6］ Colorni A，Dorigo M，Maniezzo V，et al.Distributed optimization by ant colonies［A］.Proceedings of the 1st European Conference on Artificial Life［C］.Paris，France：Elsevier Publishing，1991：134－142.

［7］ Dorigo M，Maniezzo V，Colorni A.Ant system：Optimization by a colony of cooperating agents［J］.IEEE Transaction on Systems，Man and Cybernetics－Part B，1996，26（1）：29－41.

［8］ 段海滨，王道波，朱家强，等.蚁群算法理论及应用研究的进展［J］.控制与决策，2004，19（12）：1321－1326，1340.（DUAN Hai－bing，WANG Dao－bo，ZHU Jia－qiang，et al.Development on ant colony algorithm theory and its application［J］.Control and Decision，2004，19（12）：1321－1326，1340.（in Chinese））