单交叉口多相位在线Q学习交通控制模型

卢守峰，张 术，刘喜敏

随着车辆保有量的增加，中国大中城市交通拥挤的时段和范围逐渐增大。对于城市的中心区，不仅是早晚高峰出现交通拥挤，而是多个时段出现交通拥挤。交通压力增大的直接体现是排队长度增加，过饱和交叉口在一个周期内不能够将排队清空。以长沙市SCATS控制系统为例，其控制原理是绿灯时间饱和度，即被车辆通行占用的绿灯时间与总绿灯时间的比值。对于过饱和交叉口，由于要通行的交通需求较大，总绿灯时间扣除车间时距几乎均被占用。这种情况下，SCATS控制系统的配时方案等同于定周期配时，绿灯期间排队车辆被放行一部分，后面的排队车辆向前挪动一部分，工作效率较低。随着交通检测器技术的发展，视频检测技术在数据采集方面已得到发展，如：全景视频技术［1］能够提供整个交叉口范围内的交通参数。排队长度较长是过饱和交叉口的主要特征，如何平衡交叉口不同相位的排队长度、综合优化整个交叉口的时间与空间资源是本研究的重点。

交通系统的运行效率由供、需两个方面决定，这两个方面都具有不确定性和动态性的特点，再加之驾驶员行为的不确定性，经过同一个交叉口的不同驾驶员具有不同的驾驶行为，即使同一个驾驶员在不同时间也会表现出不同的驾驶行为。这决定了状态集的数量很大，难以事先枚举出所有状态，为每种状态都存储一个最优方案很困难。提高交通控制系统的智能性是当前研究的一个趋势。对于交通控制系统而言，智能最重要的体现是具有学习能力。如果交通控制模型具有了学习能力，那么就可以记住经验、对未经历的状态采取经验复用。利用强化学习理论，建立具有学习能力的交通控制模型最具代表性。该方法能够学习控制行为与其对环境作用效果之间的关系，近些年来被应用于交通控制系统研究。Oliveira［2－3］等人采用基于环境检测的强化学习方法，对噪音环境下的配时优化进行了研究，通过检测环境的改变来学习动态的流量模式，自动对流量模式进行识别，执行对应的策略，跟踪环境转换的预估误差和奖励。Chen［4］等人研究了一种基于近似动态规划的自适应交通信号实时控制算法，利用线性近似函数代替动态规划中的值函数，其中线性近似函数的参数由时间差分强化学习和扰动强化学习两种方法在线学习，极大地提高了模型的计算效率，而且模型优化的时间步长越小，其性能越优。Wiering［5］等人研究了基于“车辆投票”的强化学习优化模型，通过估计每个车辆的等待时间，决定配时方案，该模型优于固定信号配时模型。Abdulhai［6］等人建立了基于Q学习模型的配时优化模型，需要对所有连续状态进行整合加以描述，计算时间随着车道数量和交叉口数量指数增加，限制了该模型只能用于小型路网。随后，Prashanth［7］等人基于函数近似的强化学习算法对信号配时优化进行了研究，提出了基于特征的状态描述方法，将状态离散为低、中和高3个区间，解决了状态—行为对的维数灾难问题。Bingham［8］使用神经网络调整模糊交通信号控制器的成员函数，使用强化学习评估神经网络采用的行为效用，改进了模糊控制的效果。马寿峰［9］等人将Agent与经验知识和Q学习算法相结合，研究单个路口的动态配时问题。承向军［10］等人采用Q学习方法以减少延误为目标对单路口进行信号配时的优化，并应用模糊控制规则改善信号控制，该方法优于定时控制和感应式控制。赵晓华［11－12］等人将Q学习及BP神经元网络应用于切换式的信号控制优化，该模型能够感知交通流变化，并能够自适应控制，与定时控制相比，具有明显的优势。卢守峰［13－14］等人在周期和绿信比等概念的基础上，分别以等饱和度、延误最小为优化目标建立了单交叉口离线 Q学习模型。Simon［15－16］等人将具有人工干预的监督学习和时间差分强化学习应用于信号配时优化。

作者以总关键排队长度差最小为优化目标，拟研究交通控制的在线学习模型。传统的Q学习模型在应用时强调构造状态与行为的并重，状态分为连续型状态和离散型状态，因此，原有模型的状态－行为组合庞大，遍历时易造成维数灾难。本研究拟对Q学习模型构建新的目标函数和新的离散化的奖励函数，对Q学习公式进行简化，弱化对状态的构造，使得排队长度小于某一长度时为一个状态，当它大于某一长度时为另一状态，将这个长度取无穷大则状态不变。使状态－行为组合简化为行为组合，以减少重复，加快学习速度。

1 Q学习模型

1.1 Q学习公式的简化及参数的取值

强化学习模型通过与动态环境交互进行决策学习，是一种试错型的学习模型，其基本原理是学习模型在某个环境状态下选择并执行某个行为，作用于环境状态并得到相应的奖励。该奖励用于强化这个环境状态与最佳行为之间的映射关系，反复执行这个过程，学习模型即可获得在任意环境状态下选择最佳行为的能力。学者们提出了多种强化学习算法［17］，比较成功的算法有：蒙特卡罗算法、瞬时差分（Temporal Difference，简称为TD）算法、Sarsa学习算法、Q学习算法、Dyna学习算法及R学习算法等。其中，应用最为广泛的是Q学习算法，被公认为强化学习算法发展过程中的一个里程碑，由 Watkins［2］于1989年提出。Q学习算法中，模型通过反复映射、迭代优化Q值函数来提高学习能力，Q函数的初始值可任意给定，Q 学习的公式［17］为：

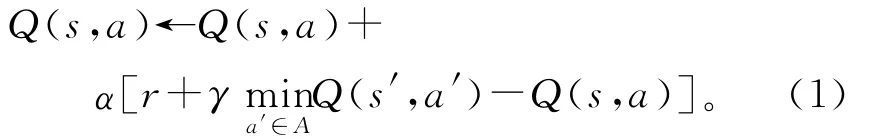
式中：α∈［0，1］为学习率；γ∈［0，1］为折扣因子；A 为行为的集合；Q（s，a）是当前状态s、行为a对应的Q 值；Q（s′，a′）是下一状态s′、行为a′对应的Q值；r是当前奖励。

当状态不改变，即s等于s′时式（1）可简化为：

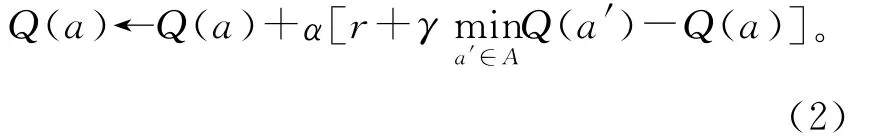
经过多次的仿真测试，对于信号配时优化问题，当α取0.1～0.2、γ取0.7～0.9时，效果最好。参数取此范围之外时，易出现两种状况：①无论学习多久，Q学习也不会收敛，即所有行为所对应的Q值都在不断增加，没有任何一个行为的Q值会连续下降；②当Q学习已收敛于某一行为时，由于Vissim中车流量服从泊松分布，可能某个时间突然到达较大的车流量，造成奖励r突然增大，造成Q值剧烈增加，从而使得Q学习模型容易跳出当前收敛状态，即干扰量对模型收敛影响很大，模型不够稳定。通过多次测试，选择参数合适的范围，使得Q学习既能收敛到最优行为又能保持足够的稳定性。

1.2 建立状态、行为、奖励的模型

建立状态、行为、奖励的模型是决定强化学习模型性能的关键。以交叉口进口的流量为状态。选取各相位绿灯时间的排列组合作为行为。定义同一相位内排队长度最大的流向为关键车流。定义关键车流的排队长度为关键排队长度。各相位关键排队长度之差的绝对值的总和为总关键排队长度之差。多个周期的总关键排队长度之差的平均值为平均总关键排队长度之差。优化的目标函数定义为4个相位的总关键排队长度之差最小。以4个相位的总关键排队长度之差最小作为目标函数是为了使4个相位的排队长度尽量相等。根据各相位排队长度实时动态分配绿灯时间，增加排队长度过长的相位的绿灯时间，使其排队不再增加或消散，减少排队长度过短的相位的绿灯时间，保证绿灯时间得到充分利用。研究中发现：这个目标函数对于相近的配时方案的取值相差不大，即不敏感。为此，利用这个目标函数重新构造了奖励。例如：l为总关键排队长度之差的当前值，l′i为各相位关键排队长度之差，l 为总关键排队长度之差的历史平均值，r为当前奖励，k为正数。以l离散为5个部分为例，说明奖励函数的构建，k取10。

如果0≤l≤0.5l，则r＝0.5k；如果0.5l≤l≤l，则r＝k；如果l≤l≤1.5l，则r＝1.5k；如果1.5l≤l≤2l，则r＝3k；如果l≥2l，则r＝5k。

离散的目的是拉大奖励的差距，从而强化学习模型能够区分行为之间的优劣。由于每个奖励对应关键排队长度差的一个区间，因此离散方法能够减少交通流随机性带来的不稳定性，提高鲁棒性。行为得到的奖励越少，说明行为越好。

对于交叉口控制，行为是各相位绿灯时间，涉及定周期和变周期两种情况。对于定周期情况，各相位绿灯时间之和等于周期减去总损失时间，行为取值受到周期的约束。对于变周期情况，行为取值不受到周期的约束，在取值范围内，分别选取各相位绿灯时间，各相位绿灯时间之和加上总损失时间即为周期。变周期模式的行为数量比定周期模式的行为数量大得多，定义域的增大为得到更优的结果提供了可能。

1.3 行为选择函数

根据Pursuit函数［17］，更新行为，选择概率。在第t＋1个周期，选择最优行为a＊t＋1的概率为：

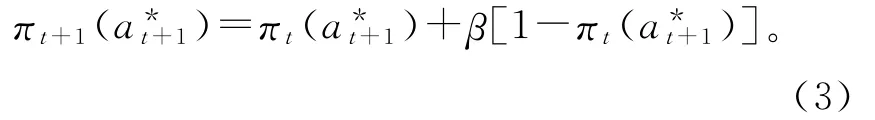
选择其他a≠a＊t＋1行为的概率为：

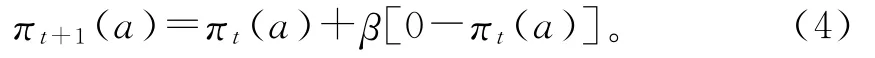
式中：πt（a）表示在周期为t时选择行为a的概率；a＊t＋1表示最优行为，在本研究中最优行为指当前状态下最小Q值所对应的行为，当有多个最优行为时随机选择一个；β的取值为0＜β＜1。

初始化行为选择概率矩阵时，每个初始行为概率都相等且概率总和为1。通过调整β，Pursuit函数既能确保以较大的概率选择最优行为，又能探索没被选中过的行为，使行为的探索与利用保持平衡。

2 在线学习流程

用Excel VBA、Vissim及Matlab集成仿真平台的方法［18］进行了研究。Excel VBA与 Matlab的集成通过Excel link扩展接口实现，Excel VBA与Vissim之间通过COM接口集成。基于这个集成仿真平台，可以实现在线和离线两种学习方法。对于离线学习方法，Matlab存储已收敛的强化学习矩阵，Excel VBA基于这个矩阵和Vissim检测到的排队长度选择信号配时方案。对于在线学习方法，Matlab存储的强化学习矩阵在每个周期都被更新一次，Excel VBA基于强化学习矩阵的当前值和Vissim检测的排队长度选择信号配时方案。随着程序的运行，通过不断地对强化学习矩阵进行更新，使得该矩阵逐渐收敛。因此离线方法和在线方法的主要区别在于强化学习矩阵。对于离线学习方法，使用收敛的强化学习矩阵，适用于波动小的交通模式；对于在线学习方法，程序边运行边更新强化学习矩阵，适用于波动大的交通模式。作者采用在线学习方法的流程可描述为：

1）启动Excel VBA、Vissim及 Matlab集成仿真平台，在VBA中，初始化行为选择概率矩阵、Q值矩阵。

2）在Matlab中，更新行为选择概率，并选取当前行为。

3）将当前行为对应的绿灯时间传回Vissim，单步运行一个周期后，提取排队长度，传回 Matlab。

4）Matlab处理数据，得到总关键排队之差及奖励。

6）判断是否满足终止条件。若不满足，则转向2）；否则，终止。

3 到达流量均值固定情况的模型性能对比分析

将定周期Q学习模型、不定周期Q学习模型与Transyt配时模型进行性能对比分析。算例设置：对于一个十字型交叉口，采用4相位控制，各进口方向直行2个车道、左转1个车道，右转不受控制。相位设置：东西直行为相位1，东西左转为相位2，南北直行为相位3，南北左转为相位4。流量设置：东西直行流量为1 168 892veh／h，东西左转流量为416 344veh／h，南北直行流量为132 272veh／h，南北左转流量为420 152veh／h。

3.1 Transyt配时方案

采用Transyt 14版本进行计算，黄灯时间均为3s，全灯时间在相位2，3之间和相位4，1之间设置，设为2s，即总绿灯损失时间为16s。相位和相序如图1所示。利用Transyt的周期优化功能，优化得到最佳周期为70s。然后，将此周期时间输入Transyt中，优化出各相位绿灯时间，按相序分别为 ［15，13，13，13］。在 Vissim 中 画 出 与Transyt同数量同宽度的车道，并输入相对应的流量，设置相同的相位时间间隔及相序，将Transyt中的流量及信号配时输入Vissim中进行仿真，提取数据的时间步长与周期相同，即每隔70s提取一次各流向关键车流的最大排队长度，仿真总步长设为2 000步。

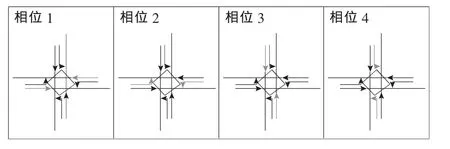
图1 相位及相序Fig.1 Phase and phase sequence

3.2 定周期Q学习配时方案

作为对比，定周期Q学习配时方案周期采用Transyt最优周期，即70s。各相位的最小绿灯时间设为10s，最大绿灯时间为24s。以2s为间隔取值，一个相位绿灯时间可选范围为［10，12，14，16，18，20，22，24］。当4个相位选择的绿灯时间总和等于70～16s时，为一个行为（总共有120个行为）。奖励为总关键排队长度之差l。 在线对Vissim进行仿真，仿真总步长设为2 000步，每步70s。各状态－行为对的初始Q值均设为47，行为的初始概率均设为1／120。单步运行，每一仿真步内用排队长度计数器采集各相位关键车流的排队长度，通过Q学习得到新的配时方案，并写入Vissim中。其仿真结果分别如图2～4所示。

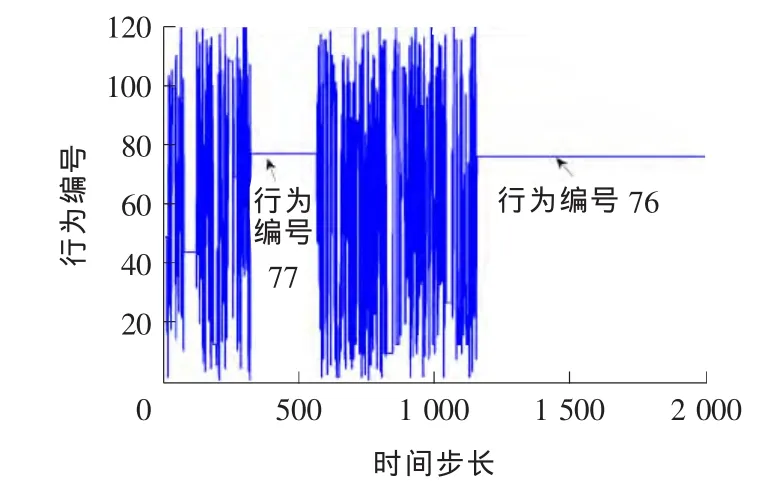
图2 行为变化Fig.2 Behavior change

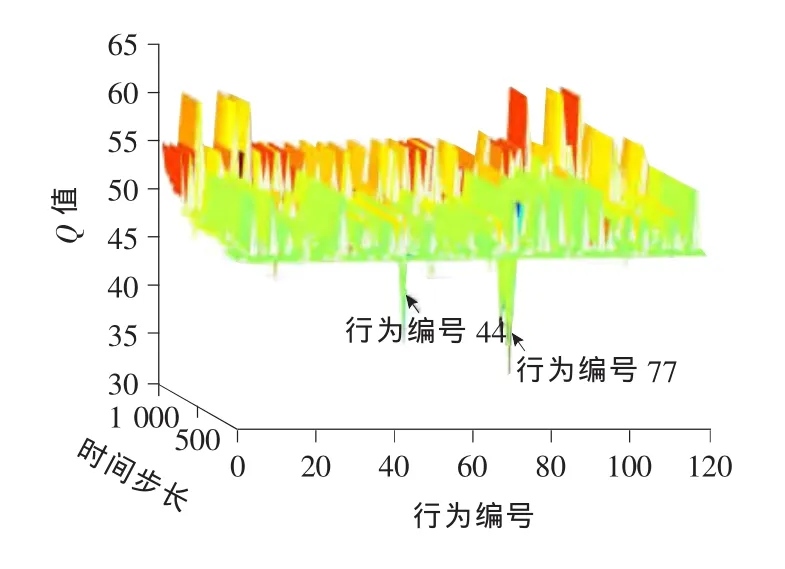
图3 前1 000步Q值变化Fig.3 The Qvalue changes before the first 1 000steps

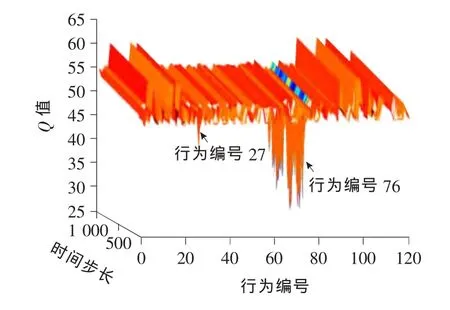
图4 后1 000步Q值变化Fig.4 The Qvalue changes after the last 1 000steps

行为编号76对应各相位绿灯时间分别为［14，14，10，16］。由图2可知，运行2 000步以后，行为选择收敛于编号76。在Q学习过程中，一个时间步内只选择一次行为，被选中的行为Q值得到更新，其他行为的Q值则保持不变。收敛即意味着同一行为被连续选中，该行为对应的Q值不断地被更新，但始终比其他行为所对应的Q值小，其对应的图像是一块底部呈锯齿状的薄片，矩形薄片表示未被连续选中的其他行为。由图3，4可知，由于Q学习具有全局探索学习的能力，即使在局部收敛于行为编号77（对应的各相位绿灯时间［14，14，12，14］）后也能继续探索新行为直至学习到最优行为76（对应的各相位绿灯时间［14，14，10，16］）。

3.3 不定周期Q学习配时方案

虽然定周期Q学习配时模型具有很好的性能，但其缺陷在于：其配时方案的优化要事先确定周期时间，即要先优化出周期，然后才能优化出各相位绿灯时间。与Transyt相同，对不同的流量要优化出不同的周期时间及配时方案，对于现实生活复杂的交通流来说，显得十分的繁琐。而不定周期Q学习配时模型则具有同时优化周期及绿灯时间的功能，能有效解决这些问题。不定周期仿真中Vissim的各种设置与定周期Vissim的一致，各相位的最小绿灯时间设为10s。为避免维数灾难以及考虑到定周期配时和Transyt配时最大绿灯时间均不超过18s，最大绿灯时间设为18s，以2s为间隔取值，一个相位绿灯时间可选范围为［10，12，14，16，18］，4个相位共有625种组合，即625个行为。周期时间为4个相位绿灯时间之和加上16s的绿灯损失时间。在线进行仿真，各状态－行为对的初始Q值均设为47，行为的初始概率均设为1／625。仿真总步长设为5 500步，每步步长等于当前周期时间，单步运行，每一仿真步内用排队长度计数器从Vissim中采集各相位关键车流的排队长度，通过学习，得到不定周期新的配时方案后，写入Vissim中，继续仿真。其仿真结果分别如图5，6所示。

从图5，6中可以看出，不定周期Q学习的最优行为是编号为354（对应的相位绿灯时间［14，18，10，16］）的行为，其对应的最优周期时间是74s。

3.4 3种方案的对比

Transyt配时方案、定周期Q学习配时方案及不定周期Q学习配时方案的性能对比见表1和如图7所示。

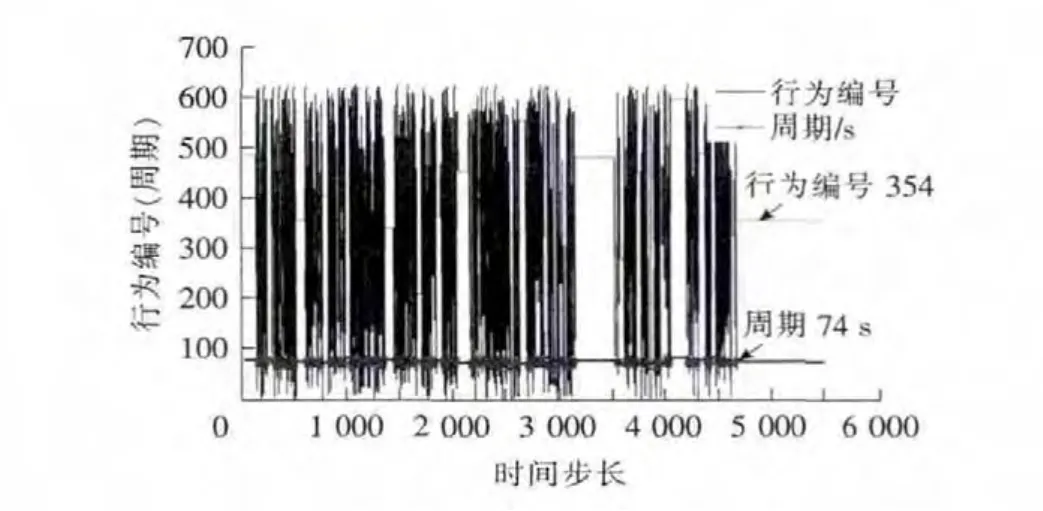
图5 行为与相对应的周期变化Fig.5 Behavior and the corresponding periodic change

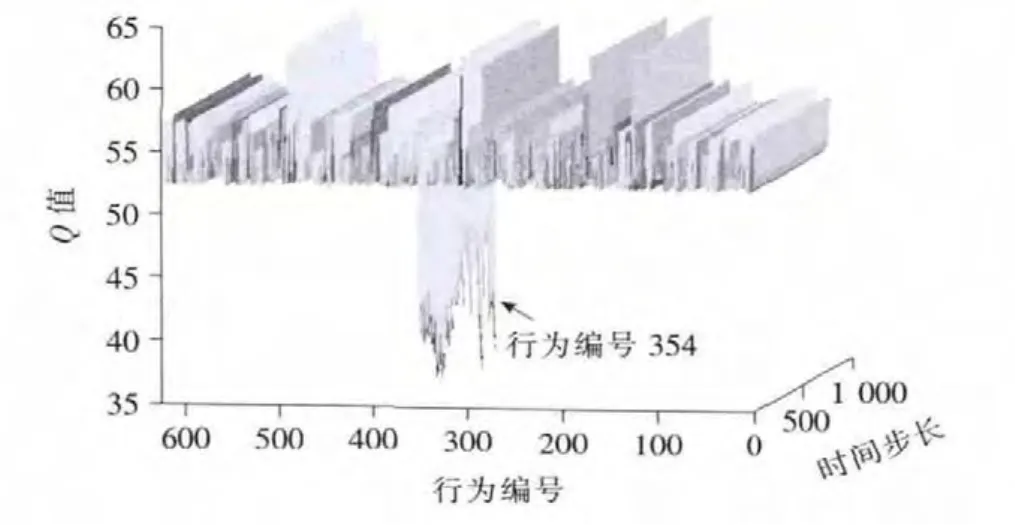
图6 最后1 000步Q值变化Fig.6 The Qvalue changes in the last 1 000steps

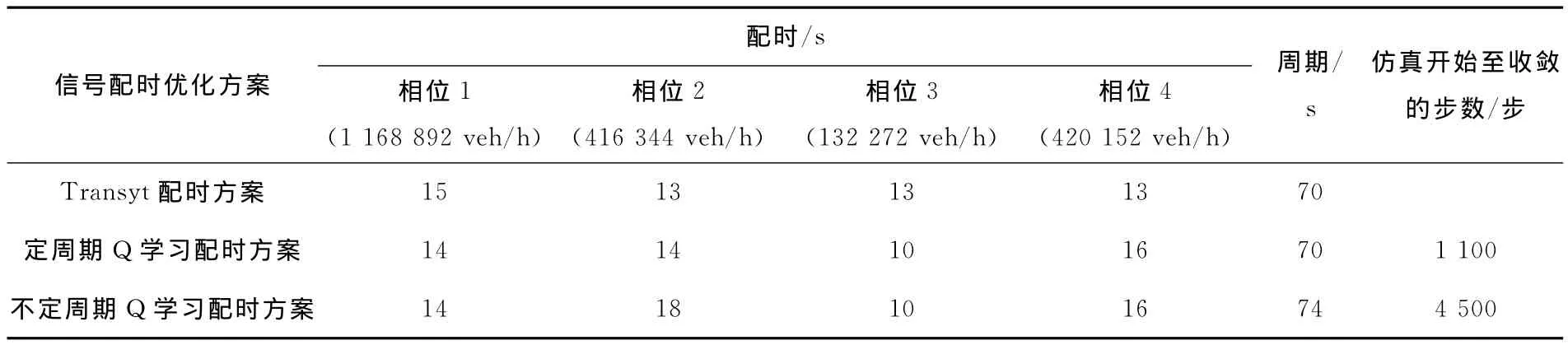
表1 相同流量下不同的配时方案Table 1 The different timing plans under the same flow

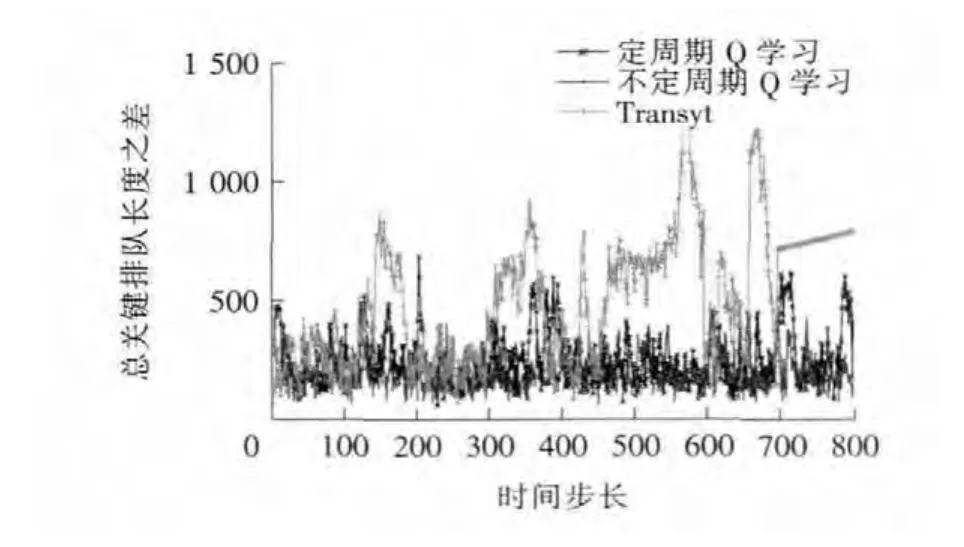
图7 行为收敛后总关键排队长度之差的对比Fig.7 The contrast among the differences of total critical queue length after behavior convergence

从表1中可以看出，定周期Q学习配时、不定周期Q学习配时与Transyt配时结果非常接近。从开始仿真到选择最优行为，定周期Q学习配时所用步数1 100步远小于不定周期Q学习配时4 500步。这说明在以周期优化为前提的情况下，定周期Q学习有更高的学习效率。从图7中可以看出，不定周期Q学习和定周期Q学习行为收敛后的配时所造成的总关键排队长度之差在平均值及波动幅度上都要比Transyt配时的要小一些。这说明Q学习模型的配时性能是较优的，且不定周期Q学习具有更好的效果。3种方案对比说明：①定周期Q学习模型的学习速度更快，在周期确定的情况下可优先考虑；不定周期Q学习模型的整体性更好，周期及各相位配时都能同时优化，且性能更好。②两种Q学习模型都具有探索全局最优行为的性能，不会陷入局部最优。

4 到达流量均值变化情况下的不定周期Q学习配时方案

由于不定周期Q学习模型具有较好的性能，因此，通过改变到达流量均值，能检验不定周期Q学习模型在流量变化状况下的学习性能。本研究中的算例计算都是以Vissim软件为平台的，在该软件中，到达流量服从输入流量的泊松分布，流量设置见表2，计算结果分别如图8～10所示。

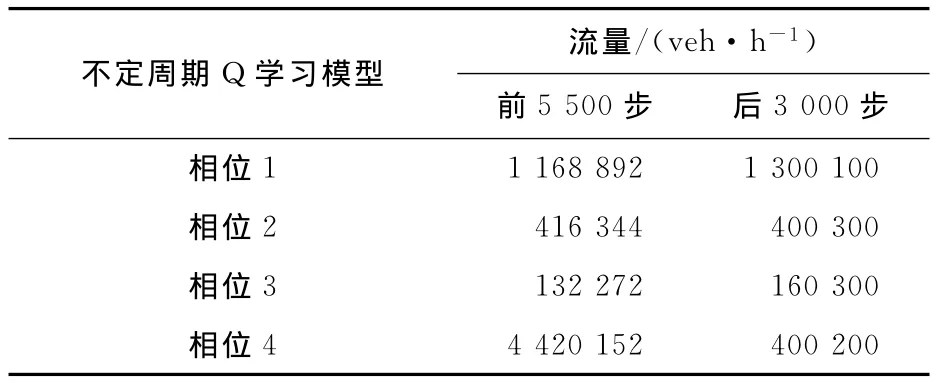
表2 流量设置Table 2 The input flow rate

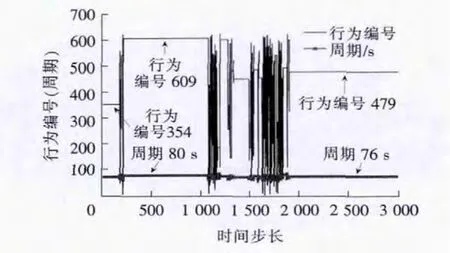
图8 流量改变后，行为与相对应的周期变化Fig.8 Behavior and the corresponding cycle

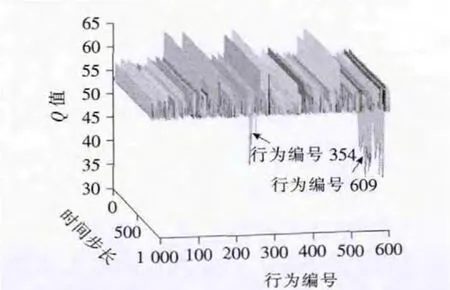
图9 流量改变后，前1 000步Q值变化Fig.9 The Qvalue changes for the first 1 000steps

从图8中可以看出，流量改变后，经过短暂探索局部收敛于行为编号609（对应的相位绿灯时间［18，18，12，16］），对应周期为 80s，经过大约2 000步的探索收敛于全局最优行为479（对应的相位绿灯时间［16，18，10，16］），对应周期为76s。第一次收敛需要4 500步，流量变化后，第二次收敛需要2 000步。可以看出，第二次收敛步数明显减少。这说明：①对于流量改变情况，不定周期Q学习模型能给出相对应的配时方案；②Q学习模型能够利用流量改变前的学习经验应对新环境，加快了收敛速度。

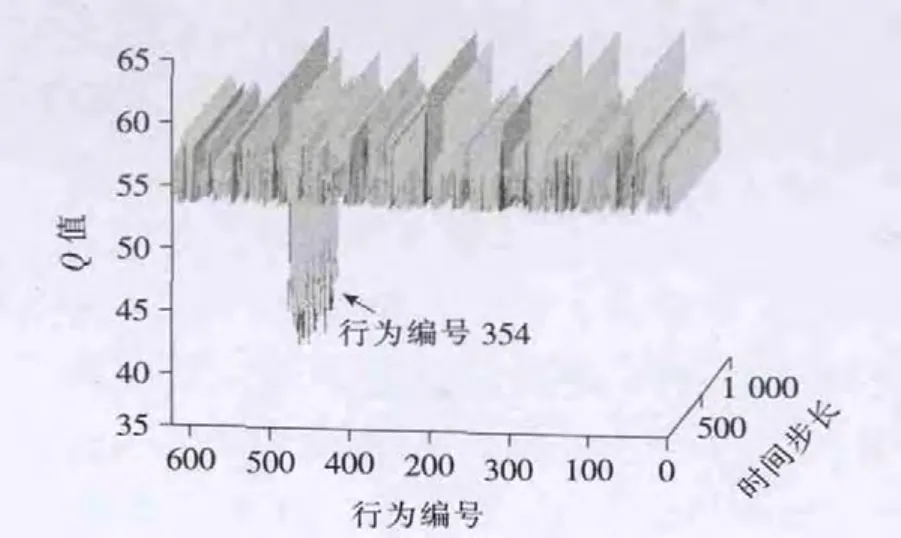
图10 流量改变后，最后1 000步Q值变化Fig.10 The Qvalue changes for the last 1 000steps

5 结论

本研究构建了新的目标函数和新的离散化的奖励函数，对Q学习公式进行了简化。通过Excel VBA、Vissim及Matlab集成仿真平台进行了研究。仿真结果表明：建立的以总关键排队长度之差最小为优化目标的单交叉口多相位在线Q学习模型能够探索全局最优行为，不会陷入局部最优，其最优配时方案比Transyt配时方案具有更好的效果。定周期Q学习模型的学习速度更快，在周期确定的情况下可优先考虑。不定周期Q学习模型的整体性更好，周期及各相位配时都能同时优化，且准确性更好。在流量改变情况下，不定周期Q学习模型能够及时适应环境的变化，较快地寻找到相应的最优配时，并且利用学习经验，加快了学习速度。

本研究建立的Q学习模型能对多相位单交叉口的周期时间及各相位绿灯时间进行动态优化，具有一定的实用价值。模型中采用的是固定的相位及相序，Q值更新公式参数是通过反复测试确定的经验值，对参数进行敏感性分析及相位和相序的优化是下一步的研究方向。

（

）：

［1］ 郑嘉利，覃团发.基于仿射运动估计的旅游景观全景视频系统［J］.广西大学学报：自然科学版，2010，35（5）：817－820.（ZHENG Jia－li，QIN Tuan－fa.Panoramic video system based on affine motion estimation for tourist landscape showing［J］.Journal of Guangxi University：Natural Science Edition，2010，35（5）：817－820.（in Chinese））

［2］ Oliveira D，Bazzan A L C，Silva B C，et al.Reinforcement learning based control of traffic lights in nonstationary environments：A case study in a microscopic simulator［A］.Proceedings of the 4th European Workshop on Multi－Agent Systems［C］.Lisbon，Portugal：［s.n.］，2006：31－42.

［3］ Ilva B C，Oliveira D，Bazzan A L C，et al.Adaptive traffic control with reinforcement learning［A］.Proceedings of the 4th Workshop on Agents in Traffic and Transportation［C］.Hakodate，Janpan：［s.n.］，2006：80－86.

［4］ Chen C，Chi K W，Benjamin G H.Adaptive traffic signal control using approximate dynamic programming［J］.Transportation Research Part C，2009，17（5）：456－474.

［5］ Wiering M，Veenen J V，Vreeken J，et al.Intelligent traffic light control，institute of information and computing sciences［R］.Dutch：Utrecht University，2004.

［6］ Abdulhai B，Pringle R，Karakoulas G J.Reinforcement learning for true adaptive traffic signal control［J］.Journal of Transportation Engineering，2003，129（3）：278－285.

［7］ Prashanth L A，Shalabh B.Reinforcement learning with function approximation for traffic signal control［J］.IEEE Transactions on Intelligent Transportation Systems，2011，12（2）：412－421.

［8］ Bingham E.Reinforcement learning in neurofuzzy traffic signal control［J］.European Journal of Operational Research，2001，131（2）：232－241.

［9］ 马寿峰，李英，刘豹.一种基于Agent的单路口交通信号学习控制方法［J］.系统工程学报，2002，17（6）：526－530.（MA Shou－feng，LI Ying，LIU Bao.Agentbased learning control method for urban traffic signal of single intersection［J］.Journal of Systems Engineering，2002，17（6）：526－530.（in Chinese））

［10］ 承向军，常歆识，杨肇夏.基于Q学习的交通信号控制方法［J］.系统工程理论与实践，2006，26（8）：136－140.（CHENG Xiang－jun，CHANG Xin－shi，YANG Zhao－xia.A traffic signal control method based on Q－learning［J］.System Engineering Theory and Practice，2006，26（8）：136－140.（in Chinese））

［11］ 赵晓华，石建军，李振龙，等.基于 Q－learning和BP神经元网络的交叉口信号灯控制［J］.公路交通科技，2007，24（7）：99－102.（ZHAO Xiao－hua，SHI Jian－jun，LI Zhen－long，et al.Traffic signal control based on Q－learning and BP neural network［J］.Journal of Highway and Transportation Research and Development，2007，24（7）：99－102.（in Chinese））

［12］ 赵晓华，李振龙，陈阳舟，等.基于混杂系统Q学习最优控制的信号灯控制方法［J］.高技术通讯，2007，5（17）：498－502.（ZHAO Xiao－hua，LI Zhen－long，CHEN Yang－zhou，et al.An optimal control method for hybrid systems based on Q－learning for an intersection traffic signal control［J］.High Technology Communication，2007，5（17）：498－502.（in Chinese））

［13］ 卢守峰，邵维，韦钦平，等.基于绿灯时间等饱和度的离线Q学习配时优化模型［J］.系统工程，2012，30（7）：117－122.（LU Shou－feng，SHAO Wei，WEI Qin－ping，et al.Optimization model of the of f－line Q learning timing based on green time equi－saturation［J］.Systems Engineering，2012，30（7）：117－122.（in Chinese））

［14］ 卢守峰，韦钦平，刘喜敏.单交叉口信号配时的离线Q学习模型研究［J］.控制工程，2012，19（6）：987－992.（LU Shou－feng，WEI Qin－ping，LIU Xi－min.The study on off－line Q－learning model for single intersection signal signal timing［J］.Control Engineering of China，2012，19（6）：987－992.（in Chinese））

［15］ Simon B，Ben W.An automated signalized junction controller that learns strategies from a human expert［J］.Engineering Applications of Artificial Intelligence，2012，25：107－118.

［16］ Simon B，Ben W.An automated signalized junction controller that learns strategies by temporal difference reinforcement learning［J］.Engineering Applications of Artificial Intelligence，2013，26：652－659.

［17］ Sutton R S，Barto A G.Reinforcement learning：An introduction［M］.Cambridge，Massachusetts：MIT Press，1998.

［18］ 卢守峰，韦钦平，沈文，等.集成 Vissim、Excel VBA、Matlab的仿真平台研究［J］.交通运输系统工程与信息，2012，12（4）：43－48.（LU Shou－feng，WEI Qin－ping，SHEN Wen，et al.Integrated simulation platform of Vissim，Excel VBA，Matlab［J］.Journal of Transportation Systems Engineering and Information Technology，2012，12（4）：43－48.（in Chinese））