基于风险避免强化学习的单交叉口配时优化
毛盈方,卢守峰
近年来,交通问题逐渐成为了制约经济发展的主要问题之一。为了解决交通问题,智能交通逐步成为大家研究的主要课题之一。强化学习就是其中重要的研究方面,并且取得的了一定的成果。强化学习的优化法则是马尔可夫决策问题的预测回报,但在实际问题中并不是最适合的法则。许多实际问题要求鲁棒性控制策略考虑回报的变动问题,尤其是在运行过程中风险较大的特殊情况。
在交通信号配时优化方面,应用强化学习的研究有了一些进展。Ilva[1-2]等人针对噪音环境建立了基于环境检测的强化学习模型对配时优化。通过检测周围环境的改变来学习动态的流量模式,自动对流量模式进行识别,执行对应的策略,跟踪环境转换的预估误差和奖励。黄艳国[3]等人把Agent技术与强化学习算法相结合,提出了基于Agent技术的交通信号控制方法。根据交叉口的实时路况信息,利用强化学习来实现自适应控制,减少路口排队车辆的平均延误时间。Wiering[4]等人研究了基于“车辆投票”的强化学习优化模型,核心理论是通过估计每个车辆的等待时间,决定信号配时方案,该模型优于固定信号配时模型。戴朝晖[5]等人采用智能体系统动态分层强化学习算法,研究未知环境下大规模学习时的“维度灾难”问题,采用基于模型的强化学习利用已有的经验来学习最优策略,大大提高系统的学习效率。卢守峰[6]等人对固定周期和变周期两种模式下的单交叉口信号配时优化进行研究,构造了等饱和度优化目标的奖励函数,建立了等饱和度和延误最小两个优化目标的离线Q学习模型,有效地解决了状态维数爆炸问题。这些模型都利用了风险中立的强化学习理论,其缺点在于风险中立的强化学习模型的稳定性与鲁棒性不是很好,同时运行过程中收敛效果不明显,速度较慢。针对该问题,作者拟提出风险避免强化学习信号配时模型,以期有效地解决风险中立强化学习模型的不足。
1 风险敏感强化学习理论方法简介
处理风险敏感最优目标问题的方法有3种:
1)最坏情况控制方法。该方法的核心是找出最坏情况下的回报。如果该情况下满足要求,那么其他较优的情况下的回报也能满足。该方法的缺陷是所考虑的最坏情况在实际状况中出现的概率很低,甚至不会出现。但对有的行业是非常必要的,特别是航空领域,其系统庞大,造价极贵,一旦出现问题,就会造成极大的损失。Heger[7]针对这种情况发展了最坏情况强化学习算法,比较纯粹的最坏情况控制,他在训练的最后阶段不考虑这种在现实中出现概率极低的情况。
2)指数效应函数控制理论[8]。该方法是通过类似的效应函数来改变逐步累积的回报,从而寻求最优策略。该方法较最坏情况控制方法取得了一定改进,然而,也存在着不足:它的等式结构不适用对应的无模型强化学习法则。同时,经过多次的运算,最优策略的不稳定性会表现出来,当前的情况在下一步没出现之前不能进行判断,存在滞后性。
3)时间差分风险敏感强化学习理论框架[9]。该理论框架是在学习过程中改变时间差分。同时,通过对算法的改进,成功并有效地解决了控制理论中的问题。本研究拟运用该框架对交叉口信号配时进行优化。
时间差分风险敏感强化学习理论:在描述马尔可夫决策问题时,给定状态集S和行为集A,一系列的状态i,j,…∈S和行为a∈A,当整个系统处在状态i时,接下来向下一个状态j转移,有多个不同的行为选择,根据不同的行为选取概率,在其中选取一个最优的行为a,pij(a)为选取行为a的选择概率。同时最后得到行为奖励gij(a)。假设行为的选取是一系列的策略(函数)π∈Л,那么π(i)是行为函数。π(i)∈A,同理Jπ(i)为状态i以后所有状态行为采取后所得到的奖励折扣期望。于是,得到这样的等式:
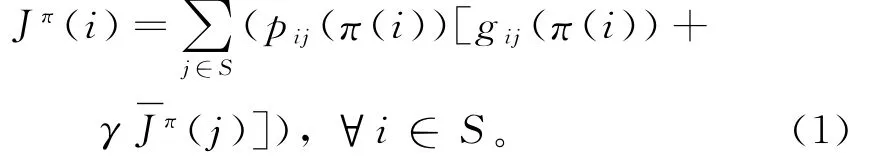
式中:γ 为折扣因子,γ∈[0,1]。
等式移项可得:
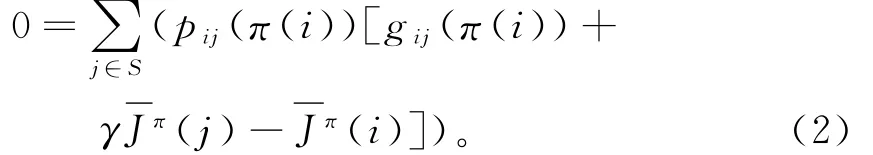
Singh[9]提出的风险敏感控制理论是:定义k∈(-1,1)的范围参数来描述风险的敏感,包括风险寻求和风险避免。定义变换函数为:
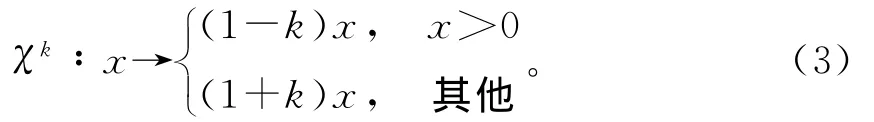
把变换函数加入到式(2)中,得到:
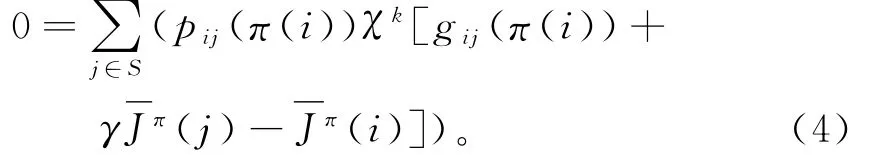
在式(3)中,如果k=0时,式(4)与式(2)是一致的,即式(2)是式(4)的一种特殊情况,此时退化为风险中立强化学习模型。当k>0时,时间差分为:gij(π(i))+γJπ(j)-Jπ(i)<0。得到的奖励小于奖励平均值;当k<0时,得到的奖励大于奖励平均值。即如果k>0,函数是趋向于风险避免;如果k<0,函数是趋向于风险寻求。
2 时间差分风险避免在线Q学习信号配时模型
在城市道路交叉口中,车辆的到达是随机的,波动性较大。一旦出现突发情况,这就对信号配时要求较高,以便解决各种情况并保证交通顺畅。保证交通的稳定性和鲁棒性至关重要。针对这种情况,构造新的信号配时控制模型:风险避免在线Q学习信号配时控制模型。
2.1 Q值更新函数的建立
对于Q值函数的研究,其中最经典的是Sutton[10]提出的,给定时刻t,观察该时刻的环境状态是s,同时选取的行为是a,然后执行行为,在接下来的时刻t+1,状态转移到s+1,系统得到了一个奖励rt,从而对Q值进行实时更新,规则为:
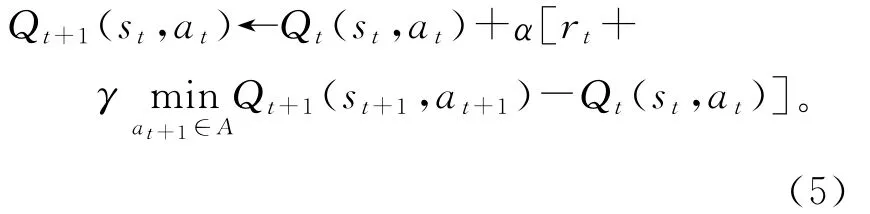
式中:st为t时刻环境的状态;at为t时刻选取的行为;Qt(st,at)为t时刻下状态行为(st,at)的Q值;Qt+1(st,at)为t+1时刻下状态行为(st,at)的Q值;rt为t时刻后的回报值;α为学习速率,α∈[0,1];γ 为折扣因子,γ∈[0,1];A 为行为集合。
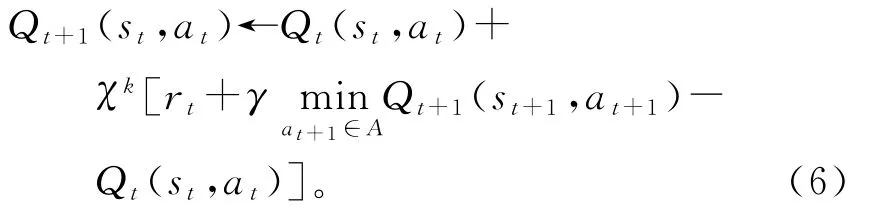
又因为在式(5)中α的取值范围为[0,1],为了保证公式的一致性,故而χk的取值必须为[0,1],但观察式(3)时,χk的取值为[0,2]。故对式(6)中χk前加入1/2进行变换:
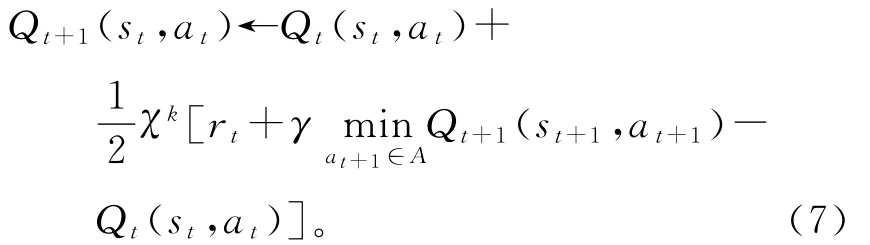
2.2 状态、行为的选择
状态是交叉口进口道的排队长度,以最简单的二相位信号配时为例,它的关键车流有2个,如果取排队长度区间[0,N],那么状态数就有N2个。在城市道路中,N 较大,这就形成了维数灾难问题,难以对状态集进行学习。因此,将排队长度区间进行离散划分,以划分为4个小区间为例,状态数减少至16个。
行为是交叉口的信号配时方案,以最简单的二相位信号配时为例,假定交叉口的配时方案的绿灯时间区间为[20,60],以2s为间隔,那么绿灯时间集合有:G={gi|i=1,2,…,21}={20,22,…,60},其中:gi表示行为编号。划分为21个行为,行为与绿灯时间的转换关系式为:(行为编号+10)×2=绿灯时间。如:行为编号g3对应的绿灯时间为26s。
2.3 奖励函数的构造
选取排队长度作为交通评价指标,利用排队长度之差的绝对值来建立奖励函数。以平均排队长度差作为基本单位将奖励进行离散,以划分成5个部分为例,见表1。
离散的目的是将不同行为对应的Q值区分开,从而将行为的选择概率区分开,好的行为选择概率增大,且不易被突然增加的排队长度造成Q值剧增和选择概率减小所影响。这样,减小了车辆到达的随机性,造成模型的不稳定性,提高了模型的鲁棒性。
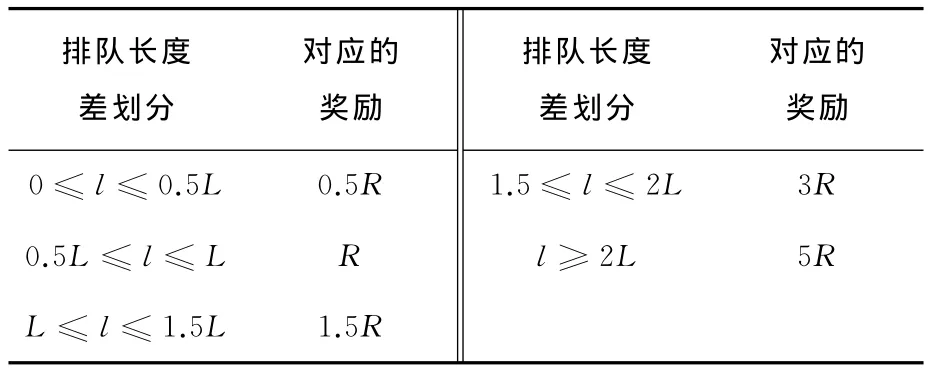
表1 奖励的构造Table 1 Reward value
2.4 行为选择机制
选取Pursuit函数作为行为选择机制,根据Pursuit函数,更新概率。当运行t个周期后,在t+1周期时,选择最优行为a*t+1的概率为:
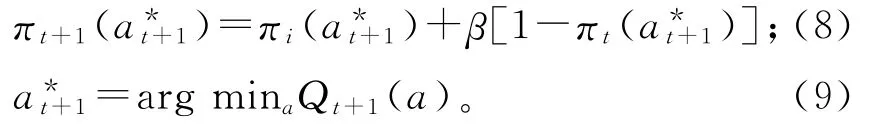
选择其他a≠a*t+1行为的概率为:
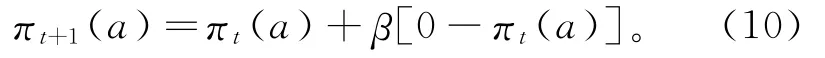
式中:πt(a)为在周期为t时选择行为a的概率;at*+1为最优行为;β的取值为0<β<1。
通过调整β,Pursuit函数既能确保以较大的概率选择最优行为,又能探索没被选中过的行为,使行为的探索与利用保持平衡。
2.5 在线学习的步骤
在线学习模式是利用强化学习算法,对实际问题进行实时交互。在交互的过程中,系统获取环境中的各种信息,得到经验,然后,利用Q值函数,通过策略,形成优化后的行为,再作用到环境中,不断地学习,逐步得到问题的最佳状态-行为对。模型中的折扣因子γ取值为0.8。
在线风险避免Q学习信号配时优化算法步骤为:
1)初始化Q值为任意值。
2)检测当前的排队长度,作为初始状态s。3)利用Q值经验,在状态对应的配时方案中,依据策略,选取配时方案a。
4)执行方案a,获取奖励r和新的状态s′。
6)更新Q 值法则:Qt+1(st,at)←Qt(st,at)+Qt+1(st+1,at+1)-Qt(st,at)]。
7)将新的交通状态s′赋予状态s。
8)重复3)~7),直到Q值收敛。
3 实例分析
选取长沙市猴子石大桥的西端上桥路口进行分析,猴子石大桥是连接长沙河西与河东的重要通道,它的交通作用非常关键,对信号配时的要求非常高。该路口是由主干道和上桥辅道构成,主要流量来自于主干道,几何线形如图1所示。
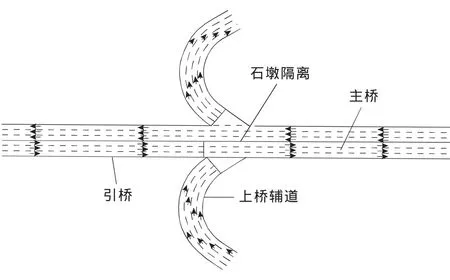
图1 猴子石大桥西路口示意Fig.1 Geometry of Houzishi bridge
根据实际调查取得的数据,主桥的流量为3 024veh/h,上桥辅道的流量为1 502veh/h。现状采用固定周期两相位信号配时,信号周期为154s。根据实测数据,主桥上的排队长度区间为[0,960]m,上桥辅道的排队长度区间为[0,400]m。设定每个相位全红时间为2s,黄灯时间为3s,每个周期绿灯总损失时间为10s。将辅道绿灯时间的选择设为学习的直接目标,设定辅道最小绿灯时间为22s,最大绿灯时间为62s。以2s为间隔,划分为21个行为,行为与绿灯时间的转换关系式为:(行为编号+10)×2=绿灯时间。在线学习的时间步长为周期时间,初始Q值设为45,行为的初始概率设为1/21。针对进口道流量较大,容易造成维数灾难,故对交通流量进行分段的离散划分。把主干道的排队长度区间[0,960]划分为4个分段,把辅道的排队长度区间[0,400],同样划分为4段,得到:Flow1={fi|i=1,2,3,4}={[0,240),[240,480),[480,720),[720,960]};Flow2={hj|j=1,2,3,4}={[0,100),[100,200),[200,300),[300,400]}。从而得出有16个状态的状态集:S={s(i,j)|i=1,2,3,4;j=1,2,3,4}={(fi,hj)|1,2,3,4;j=1,2,3,4}。
为了验证模型的效果,采用本课题组开发的集成VISSIM、ExcelVBA及Matlab的仿真平台[11]进行研究。在仿真平台上,在线风险避免Q学习信号配时优化算法步骤的实例运行为:
1)在Excel中建立初始矩阵,取35为初始值。
2)在VISSIM中获取猴子石大桥的西端上桥路口主桥和辅道上的排队长度,检测得到关键排队长度,并与Flow1和Flow2进行比对,得出相应的i和j,并利用公式State=(i-1)×4+j,得到状态。
3)利用Q值矩阵,在该状态对应的21个行为中,依据行为选择机制,选取最优的行为,即最优的配时方案。
4)对选取的配时方案进行仿真,再次得到两个方向的关键排队长度和新的状态,同时根据奖励函数和排队长度,获得对应的奖励,即排队长度差。
5)把4)中获得的相应数据代入rt+γ·Qt+1(st+1,at+1)-Qt(st,at)中,得到时间差分,判断正、负,选取χk。
6)根据式(7),对Q值进行更新。
7)将新的交通状态s′赋予状态s。
8)若Q值矩阵不收敛,重复3)~7);否则,结束。
根据步骤和式(7),分别选取k=0.1和k=0.9,来探索k取值的不同对应信号交叉口配时的影响。分别在仿真平台上运行多次直至收敛,一次为一个信号周期。然后,选取其中一个迭代次数较多的状态(2,2),进行对比分析,如图2所示。
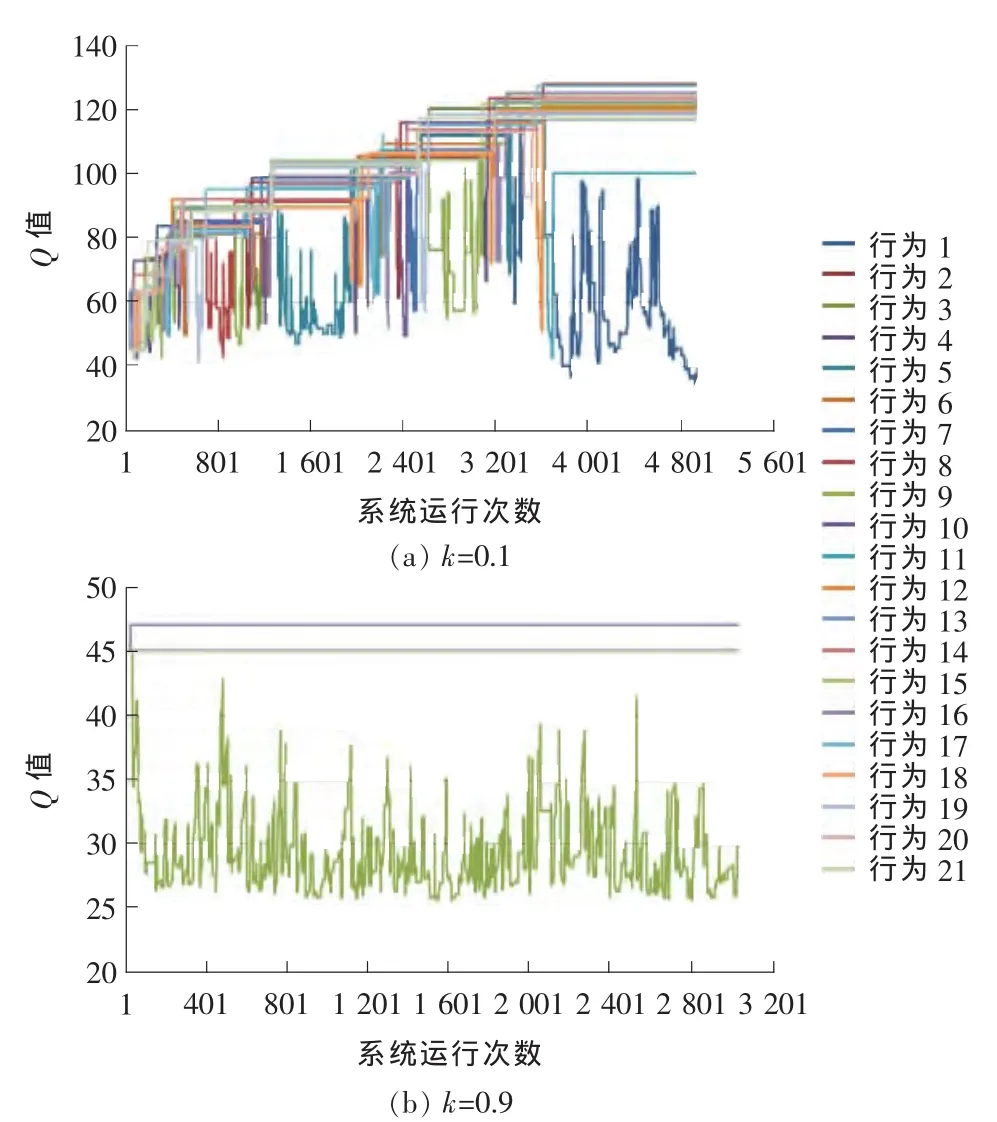
图2 k=0.1和k=0.9时,Q值运行情况对比Fig.2 Qvalues for k=0.1and k=0.9
图2 中,不同颜色的线条表示21个不同的行为,横线表示在运行中系统许久没有选取该行为了,线条的连续波动表示系统连续选取了该行为。如果一条波动线一直保持在21条线的最低Q值且连续跳动,则表示在该状态下系统收敛于该行为。k越大,风险避免的程度越高。如:k=0.1时,状态(2,2)的收敛出现在系统运行3 600次时;而k=0.9时,在系统运行100次时就开始收敛了。对于配时方案的稳定性,二者达到收敛后都较稳定。对于k=0.1时,状态(2,2)收敛于行为1,得到的两相位绿灯时间为(22,122)s。收敛后的主干道平均排队长度为230.35m,辅道平均排队长度为150.01m,排队长度差为80.34m。对于k=0.9时,状态(2,2)收敛于行为9,得到的两相位绿灯时间方案为(38,106)s。收敛后的主干道平均排队长度为274.82s,辅道平均排队长度125.01s,排队长度差为149.81m。总的来说,k越大,收敛性越好且越快,但它探索的行为的个数较少。k分别取0.1和0.9时,它们的性能差别较大。
为了寻求既能保证收敛又能有较好性能的学习方法,采用将k小步距递增的方式。提出在仿真过程中,可以等比例地把k从0逐步增加趋近于1,共运行10 000次,k从0以0.1为步长逐步增加至0.9。然后与风险中立的Q学习交通信号配时算法进行对比。运行10 000步后,取运行次数较多的前8个状态进行对比分析,得出结果见表2。
从表2中可以看出,风险避免的Q学习交通信号配时算法在运行相同次数时,收敛状态的个数较多,收敛速度较快,同时配时方案效果也较好。这说明该方法运用在交叉口信号配时控制中较为理想。
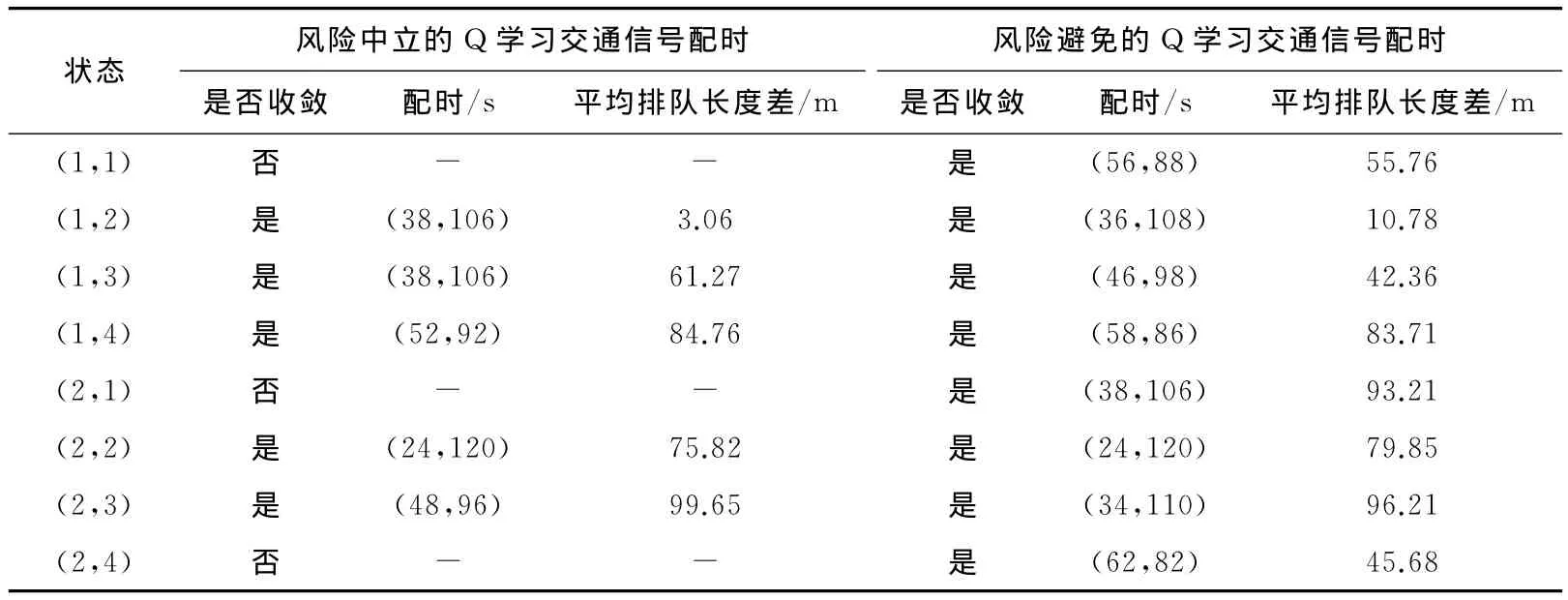
表2 结果分析对比Table 2 Comparative analysis
4 结论
本研究建立了风险避免Q学习交通信号配时在线学习模型,相对于已有文献的风险中立的Q学习模型配时方案的稳定性有较大改进,收敛速度更快。风险避免程度越大,收敛速度越快,模型越稳定。针对风险系数k的变动进行了分析,并分析了它对配时方案和收敛性的影响。与风险中立Q学习模型相比,平均排队长度差相当,但是,能够保证模型收敛,且速度较快。因此,针对交通信号配时优化这类问题,由于其随机性较大、干扰因素较多,应该采用风险敏感强化学习模型。又由于k的取值不同对模型的性能有较大差别,因此,采用k小步距递增的方式,适合于交通信号配时优化。
(
):
[1] Oliveira D,Bazzan A L C,Silva B C,et al.Reinforcement learning based control of traffic lights in nonstationary environments:A case study in a microscopic simulator[A].Proceedings of the 4th European Workshop on Multi-Agent Systems[C].Lisbon,Portugal:[s.n.],2006:31-42.
[2] Ilva B C,Oliveira D,Bazzan A L C,et al.Adaptive traffic control with reinforcement learning[A].Proceedings of the 4th Workshop on Agents in Traffic and Transportation[C].Hakodate,Japan:[s.n.],2006:80-86.
[3] 黄艳国,唐军,许伦辉.基于Agent的城市道路交通信号控制方法[J].公路交通科技,2009,26(10):126-129.(HUANG Yan-guo,TANG Jun,XU Lunhui.City road traffic signal control method based on Agent[J].Highway Traffic Science and Technology,2009,26(10):126-129.(in Chinese))
[4] Wiering M,Veenen J V,Vreeken J,et al.Intelligent traffic light control,institute of information and computing sciences[R].Dutch:Utrecht University,2004.
[5] 戴朝晖,吴敏.基于混合抽象机制的多智能体系统动态分层强化学习算法研究[D].长沙:中南大学,2011.(DAI Zhao-hui,WU Min.Multi-agent dynamic hierarchical reinforcement learning based on hybrid abstraction[D].Changsha:Central South University,2011.(in Chinese))
[6] 卢守峰,韦钦平.单交叉口信号配时的离线Q学习模型研究[J].控制工程,2012,19(6):987-992.(LU Shou-feng,WEI Qin-ping.Study on off-line Q-learning model for single intersection signal timing[J].Control Engineering,2012,19(6):987-992.(in Chinese))
[7] Heger M.Consideration of risk and reinforcement learning[A].Machine earning:Proceedings of the E-leventh International Conference[C].San Francisco:Morgan Kaufmann Publishers,1994:105-111.
[8] Howard R A,Matheson J E.Risk-sensitive markov decision processes[J].Management Science,1972,18(7):356-369.
[9] Singh S.Risk-sensitive reinforcement learning[J].Machine Learning,2002,49(2-3):267-290.
[10] Sutton R S,Barto A G.Reinforcement learning:An introduction[M].Cambridge,MA:MIT Press,1998.
[11] 卢守峰,韦钦平,沈文,等.集成 VISSIM、ExcelVBA和MATLAB的仿真平台研究[J].交通运输系统工程与信 息,2012,12(4):43-48.(LU Shou-feng,WEI Qin-ping,SHEN Wen,et al.Integrated simulation platform of VISSIM,Excel VBA and MATLAB[J].Journal of Transportation Systems Engineering and Information Technology,2012,12(4):43-48.(in Chinese))

