基于元胞自动机的城市道路偶发性拥堵交通行为模拟

吴义虎，李意芬，喻 伟，喻 丹

城市交通拥堵通常分为两类：常发性拥堵和偶发性拥堵。常发性拥堵是由交通需求超过道路通行能力造成的，如：城市道路在上、下班高峰期出现的拥堵现象。偶发性拥堵是指路网因某种交通事件（如：道路交通事故和道路损毁等），使路段通行能力下降，而导致的交通拥堵，具有偶然性。偶发性拥堵产生的原因是由突发事件造成的交通需求突然增加或道路通行能力的突然降低。偶发性拥堵是随机出现的，事前不可预知其出现的时间和地点，交通疏散难度大，会严重地影响路网运行效率。局部路段偶发拥堵时，若拥堵疏散控制不及时或控制策略不佳，容易引起拥堵漂移，拥堵会向车流的上游传播，有可能在上游交叉口形成死锁现象。这类偶发事件的特性有：①空间和时间上的随机性：事件发生的时间和地点无法预测，很难事先制定具体的应急方案。②衍生性：偶发事件在造成局部路段交通通行能力大幅下降的同时，容易引起拥堵漂移，进一步引发其他区域的大面积拥堵。

偶发性交通拥堵在日益严峻的城市交通网络中产生越来越大的影响，已成为道路交通拥堵的主要问题之一，而引起许多学者关注，并开展相关研究。国内、外相关研究集中在两个方面：①突发事故引起的偶发性拥挤传播规律，主要研究了交通事故发生后交通拥堵传播在空间和时间上的特性，事故发生地点、占道宽度、道路面积和长度等因素对交通拥堵传播的影响［1］；②偶发性拥堵消散控制策略，分析了道路部分车道禁行、交通信号引导在降低偶发性交通拥堵上的效果差异，采用临时车辆放行措施，制定了适应具体交通路网特征的拥堵消散控制策略［2－5］。作者拟考虑驾驶人性格差异，建立一种描述城市偶发性交通拥堵区域交通行为的元胞自动机仿真模型，分析城市主干道拥堵的形成规律与传播机理，对交通管理部门控制偶发事件诱发的偶发性拥堵有一定的借鉴意义。

1 基于元胞自动机的交通流模型

作为一种在时间和空间上都离散的动力学模型，元胞自动机模型已广泛用来描述非线性问题，尤其适合于交通流这样复杂系统的动态时空演化模拟。元胞自动机（cellular automaton，简称为CA）由一系列的模型规则构成，而其他动力学模型则由严格的方程和函数组成。元胞自动机模型实际是一类拥有相同规则的模型的总称，主要由元胞、元胞空间、邻居及规则组成。元胞是元胞自动机最基本的组成单位，它分布在离散的元胞空间中，本身为离散的且具有限个状态。它是一个离散的空间网点集合，可以是任意维数的欧几里得空间划分，具有几何形状和边界条件。邻居用来描述系统的动态行为，在元胞与元胞空间所表述的静态之外，通过规则演化来表述元胞的状态变化。规则定义在一个或多个元胞范围内，是根据元胞与相邻元胞状态确定下一时刻状态的转移函数。根据局部范围规则，元胞下一时刻的状态取决于它与相邻元胞的状态，相邻元胞在规则之中便定义为邻居。

对于一维单车道CA交通流情况，Nasch模型［6－7］是最典型的一种，模型中的每个元胞代表一个空闲位置或是一辆具有离散数字代表车速的车辆。设dn（t）为车头间距，xn（t）是车辆在某一时间的位置函数。加速与减速规则是对车辆在道路上安全行驶速度变化情况的表述，每位驾驶人都希望车速能保持尽可能大的数值，但同时出于安全考虑，在与前车接近时，开始以概率p减速来保持一个安全的车头间距。驾驶人行为因素的影响采用随机慢化概率来描述，它受道路上各种随机因素的影响，如：驾驶人驾驶车辆时的各种随机行为（如：时走时停现象）。因为是一维模型，只能模拟单车道情况，每个元胞所代表的车辆只需考虑其前、后方的元胞状态，在4条规则下进行状态的转移。这4条规则为：①加速规则，vn（t）＝min（vn（t）＋1，vmax），如 果 车 辆 速 度 没 有 达 到vmax，增加1；②减速规则，vn（t＋1）＝min（vn（t），dn（t）），如果车辆速度vn与前车速度之差与时间的乘积大于前车车头间距dn，则vn降至vn（t）－1；③随机慢化，vn（t＋1）＝ max（vn（t）－1，0），即车辆速度vn以概率p降低1；④位置更新，xn（t＋1）＝xn（t）＋vn（t），车辆以新获取的速度向前更新位置。

假定车辆随机分布在一维离散的格点链上，vn和xn分别表示第n辆车的速度和位置；vmax为最大速度。Nasch模型将车辆演化过程分为加速、减速、随机慢化及位置更新4个阶段。

在这4条规则下，车辆运动能再现道路交通中单台车辆行驶速度的分散现象。由于NS单车道模型的特点，它简洁地描述了道路交通流的一部分现征，可实现单车道的模拟。但对于实际交通流中大量存在的车辆换道情形却缺乏考虑，国内、外许多学者通过研究道路上车辆换道行为，结合实际驾驶情况，提出了适用于实际交通流的元胞自动机模型。其中，Chowdhury［8］提出了对称双车道元胞自动机模型（STCA），该模型在NS模型的基础上提出了符合现实交通流状态的“双车道换道规则”，按NS模型进行状态更新，且按设定的规则进行换道，即：

1）dn，fore＜min（vn（t）＋1，vmax），表示第n 辆车在原车道受到阻挡。

2）dn，other，fore＞dn，fore，表示该受阻车辆可以在另一车道上达到更快的速度。

3）dn，other，back＞dsafe，表示如果换道，安全换道间距符合条件，即另一条车道上，后方的车辆与其有一定距离。

在 这 3 条 规 则 中，dn，fore、dn，other，fore以 及dn，other，back分别为第n 辆车与前方车辆的间距、与相邻车道前方车辆的间距及与相邻车道后方车辆的间距；dsafe为模型中限定的安全换道间距。在STCA模型中，dsafe＝vmax。只有当这3条规则同时满足时，cn（t）＝1－cn（t）。其中，cn为第n 辆车所在车道，且cn＝1或0。

2 车辆换道模型

STCA模型是模拟双车道交通流较为成功的模型，但考虑到城市道路偶发性拥堵发生时，车辆的换道间距并不容易产生，而实际情况是即使在拥挤的路段，仍然存在着换道行为。根据这种情况，王永明［9］等人提出了通过设置挤车变道规则，对STCA模型进行了改进，以更加符合实际的拥挤路段，建立了拥挤车流的车辆换道元胞自动机CACF模型。在拥堵的交通流中，当车辆间不存在换道间距时，前方多辆车停滞不前，短期内无法前行。当相邻车道的车辆缓慢前行时，车辆之间存在着空隙，一部分驾驶人存在希望尽快前行的心理，会采取强行变道的行为，以达到前行的目的。换道时后方车辆根据前方转向灯的指示减速，以避免追尾事故发生。而另一部分驾驶人因为谨慎或是看不到事故前方的车道，短期内不能前行，也不会轻易选择变道行为。

CACF模型中的拥堵变道规则要求同时符合空间条件和堵塞条件，即当本车道发生堵塞时，前方至少3辆车停滞不前（堵塞条件），此时邻车道元胞及邻车道前方元胞同时为空，满足挤车变道的条件（空间条件）。拥堵变道过程如图1所示。

图1 强行变道示意Fig.1 Scheme of the forced change of lanes

图1 中，数字表示车辆的速度，t时刻车辆a满足拥堵变道条件，通过转向灯准备换道，同时后方车辆b减速以避免追尾，t＋1时刻车辆a完成换道。将交通流分为非拥堵交通流和拥堵交通流。

1）非拥堵交通流的换道规则

非拥堵交通流中车辆遵循STCA模型建立的规则进行更新并加入驾驶人行为因素的影响，即车辆换道的条件满足时，仅以一定概率p0发生换道（设p0＝0.7）。

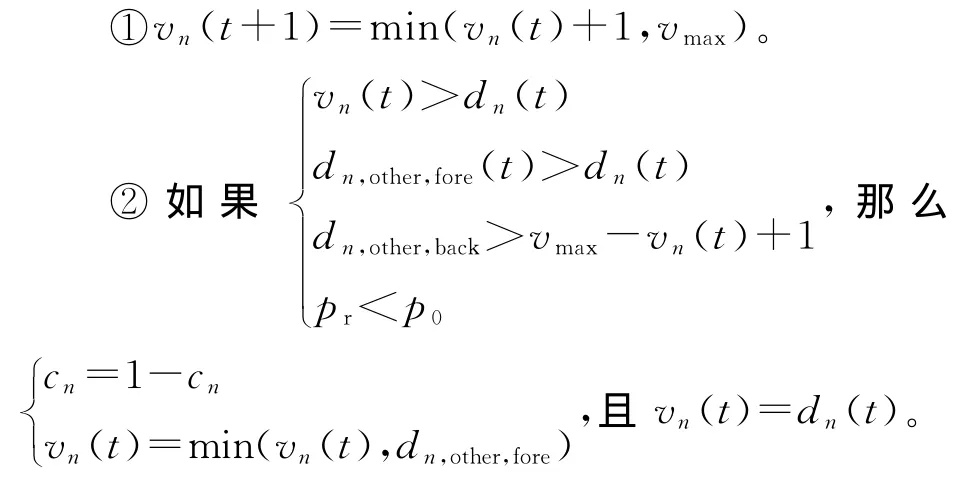
③如果pr＝p1，那么vn（t）＝max（vn（t）－1，0）。

在非拥堵交通流的情况下，①为前进规则，②为非拥堵条件下的换道规则。当前方发生阻挡而相邻车道前方没有阻挡时，dsafe＝vmax－vn（t）＋1，保证换道时后方车辆在下一个时间步不会发生碰撞，pr为随机概率，模拟驾驶人行为因素。当pr小于p0（设p0＝0.7）时，发生换道［10］。③为随机慢化。

2）拥堵交通流的换道规则

对于拥堵交通流中的车辆，当空间条件和堵塞条件都满足时，同样以一定概率p1发生换道（设p1＝0.95）。

①挤车换道：

②后方车辆减速：

因此，拥堵交通流的换道规则为：在满足前方3辆车停滞不前的拥堵条件下，同时符合拥堵变道的空间条件时，以概率p1进行变道，前方车辆换道时以转向灯为信号开始减速，否则，按照非拥堵交通流的规则更新［11］。

3 偶发性拥堵道路交通流模型

考虑在单向双车道的路段上由偶发性事件引起的交通拥堵，此时事件发生点附近的车辆行为将会发生变化。主要表现在事件的发生区域和上游区域的车辆普遍将减速行驶，并根据拥堵的发生车道，适当地选择换道；而在拥堵的下游区域，此时，车辆普遍会加速行驶以尽快离开拥堵区域。综上所述，将主干道偶发性拥堵分4个区域进行分析，分别是上游区域、核心区域、下游区域以及正常区域，如图2所示。考虑驾驶人行为因素，对不同的区域分别进行分析。

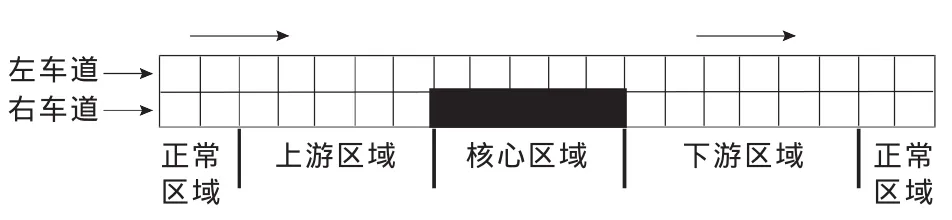
图2 道路拥堵示意Fig.2 Scheme of the congestion on the road

3.1 偶发性拥堵上游区域的CA规则

设定偶发性交通拥堵的上游区域为距拥堵事件发生点上游150m开始，向车流上游延伸到300m处范围内的区域。拥堵发生后，车辆排队开始向上游蔓延，导致上游车辆缓慢前行，随着排队长度的增长，在距离事发地点较远处，因为无法确定发生交通事故的确切车道，大部分车辆选择低速前行，由于驾驶人有尽快前行的愿望，出现换道情形时以正常换道随机进行，可采用CACF规则，因此偶发性交通拥堵的上游区域属于正常换道，并设换道概率p＝0.5。

3.2 偶发性拥堵核心区域的CA规则

偶发性交通拥堵的核心区域设定为事件发生地点至向上游延伸150m范围内的区域。在拥堵核心区域内，交通流为拥挤交通流，所有的换道都为挤车换道，在发生拥堵车道上的车辆由于能够判断出本车道的前方发生了拥堵，车辆无法在这条车道通行，因此该车辆驾驶人表现出强列的换道意愿，一旦拥挤换道的条件满足，便会采取换道行为，设换道概率p＝1，符合拥挤状态下的CACF规则；相反，在未发生拥堵车道上的车辆发现在本条车道的前方并未发生拥堵，换道概率p＝0，即车辆保持不换道且时停时走的低速行驶，考虑到不会发生换道行为，可以使用单车道NS模型进行模拟［12－13］。

3.3 偶发性拥堵下游区域的CA规则

设定拥堵下游区域为从事件发生地点至车流下游150m范围内的区域。在偶发性拥堵的下游区域，在车辆离开事件发生地点时，由于想尽快摆脱刚刚在拥挤状态下缓慢前行甚至是停止无法前行的状态，驾驶人会产生加速行驶的愿望。因此，在每一个CA仿真的时间步内，离开事件发生地点的车辆会首先观察前方离本车最近的车辆，然后选择在与自己相距最近车辆的不同车道加速前行。

拥堵下游区域的CA规则用公式表示为：

1）如果dn＜dn，other，那么车辆换到相邻车道；

2）如果dn≥dn，other，那么车辆不换道。

其中：dn为在离开事件地点后与在同一车道的前方最近车辆之间的距离；dn，other为与自己在不同车道的前方最近车辆之间的距离。

3.4 其他区域的CA规则

离偶发性拥堵事件有一定距离的其他区域，因为不满足拥挤条件下的挤车变道，故可按照STCA模型的规则进行处理。

4 仿真实验

基于改进的元胞自动机建立数学模型，通过MATLAB7.0对双车道路线核心区域进行仿真模拟［14］。模拟选择直线双车道主干道拥堵的核心区域，拥堵事件占用一个车道，实验中首先假设车辆正常行驶，在其中某个时间步产生拥堵事件，随后拥堵事件消除，仿真整个过程中拥堵产生、拥堵过程中及拥堵消散后的道路交通流情况，即交通流中车辆平均速度和车辆排队长度的实时变化情况。

4.1 实验参数选择

考虑一条长1km的单向双车道主干路，设元胞长度5m，共有200个元胞，整个路段为400个元胞，同一时刻一辆车占用一个元胞，通过MATLAB在离散的时间（s）步中进行模拟，在每一个时间步中，先根据前方车辆判断本车的前进步数，然后根据换道规则来判断本车是否换道，总共设200s，在第50秒时刻其中一车道发生交通事件。

为仿真不同交通流密度情况下的交通行为，分别模拟低密度与高密度下的交通流，实验中设置低密度车流（密度为0.5辆车／元胞）和高密度车流（密度为1辆车／元胞），设非拥堵交通流的换道概率为0.7，拥堵交通流的换道概率为0.95。

4.2 仿真实验结果与分析

1）高密度下拥堵车辆平均速度和排队长度

仿真路段内所有车辆的平均速度如图3所示，其中第50秒发生拥堵事件，至第100秒拥堵消除，拥堵事件发生时路段平均速度呈下降趋势，事件发生前和事件消除后平均速度保持平稳的变化。仿真路段内车辆排队总长度如图4所示，在高密度的情况下，当没有发生拥堵事件时，由于车辆密度较大以及受车辆随机换道的影响，也会有短暂的排队事件产生。在偶发事件产生时，则会伴随道路拥堵事件，出现明显的排队现象，并导致车流平均速度下降。

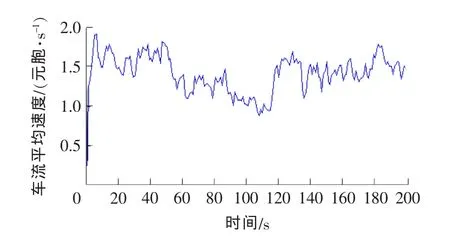
图3 高密度下的车流平均速度Fig.3 Vehicles’average speed under the high density of the traffic

图4 高密度下的车辆排队长度Fig.4 Vehicles’queuing length under the high density of the traffic

从第50秒发生偶发事件后，平均速度明显地下降，而此时排队长度开始上升，在第100秒时偶发事件取消，但平均速度与排队长度并没有立即恢复原来的状态。这说明在拥堵结束以后，事件对交通流的影响仍然存在，与实际道路交通流情况相同［15］。因此，交通事故排除后的一段时间内，仍然需要加强交通路段的管理，直到排队消除，平均车速恢复，以避免再次引发拥堵。

2）低密度下拥堵车辆平均速度与排队长度

仿真路段内低密度情况下的车流平均速度变化情况如图5所示。在拥堵事件发生过程的时间段内，速度仍然受到事件的影响，但受影响的时长相当于高密度车流明显减少。仿真路段内低密度情况下车辆排队长度如图6所示。当没有发生拥堵事件的前50s内，车辆因为随机换道和自由流也有很小的排队长度现象，比在高密度下的降低了很多。

图5 低密度下车流平均速度Fig.5 Vehicles’average speed under the low density of the traffic

图6 低密度下车辆排队长度Fig.6 Vehicles’queuing length under the low density of the traffic

低密度下车辆在第50秒至100秒偶发交通事件发生的时间段，平均速度和排队长度受到了交通事件的影响。相对于高密度的情况，拥堵事件产生时段的排队长度明显地下降了，但事件消除后仍会有一段时间的排队现象没有立即消除，同时拥堵事件对车速和排队长度产生影响的时间较高密度情况下的有明显的推后，在第70秒时平均速度开始出现下降，到了第80秒排队长度才开始快速上升。

3）偶发性拥堵事件不撤除拥堵车辆排队长度

当交通事件发生后长时间不撤除，拥堵车辆排队长度的仿真结果分别如图7，8所示。

图7 高密度下交通事件不消除时的排队长度变化Fig.7 Changes of queuing length with the traffic accident under the high density of the traffic

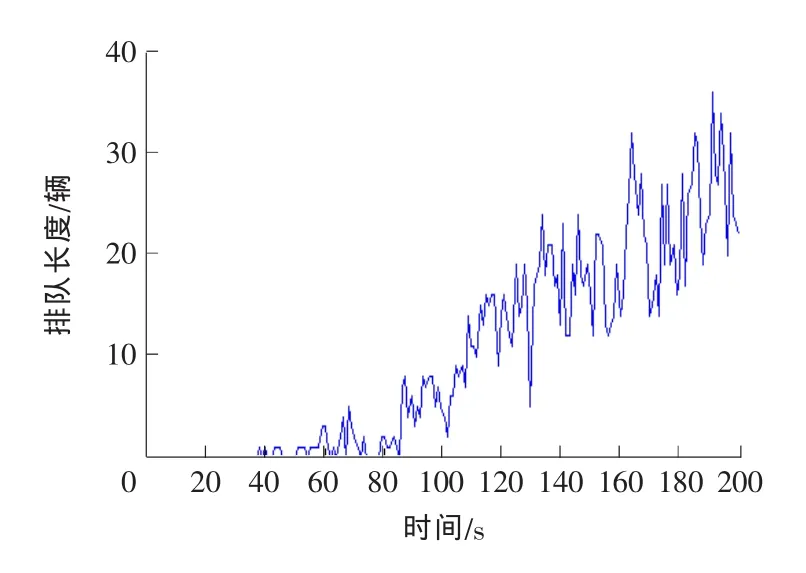
图8 低密度下交通事件不消除时的排队长度变化Fig.8 Changes of queuing length with the traffic accident under the low density of the traffic

从图7中可以看出，高密度车流时，在第100秒发生偶发性拥挤，且事件暂不撤除时的车辆排队变化情况，排队长度在拥挤发生后一直处于直线上升的趋势。如果事件不消除，排队长度一直延续增长下去，将堵塞整条道路，上游路口车辆无法进入，拥堵将蔓延至其他道路，最终影响整个交通网络。

从图8中可以看出，低密度车流时，发生偶发性事件排队长度虽然也在增长，但增长相对高密度车流的要平稳缓慢，即使拥堵事件暂不消除，经过一段时间后，排队长度缓慢增长至某个平稳值，之后不再有太大的变化。

5 结论

1）以元胞自动机模型为基础，在传统的车辆换道规则上引入驾驶人行为因素，建立了一种适用于城市道路偶发性拥堵交通流行为分析的元胞自动机改进模型。其主要特点是：将道路偶发性拥堵分4个区域进行分析，分别是上游区域、核心区域、下游区域以及正常区域。根据不同区域交通流特点和驾驶行为特点，给出了不同的车辆换道规则。

2）运用建立的模型，模拟了城市道路偶发性拥堵区域的交通流行为，对比了在不同交通流密度道路上发生拥堵事件时车辆平均速度和排度长度的变化情况。模拟结果表明：在高密度交通流情况下，短时交通事件产生的通行能力降低的影响相对于低密度交通流的情况更严重，这与实际道路交通流的情况相符合。

3）运用建立的模型可以模拟城市道路不同路段偶发性拥堵区域的交通流行为，对城市道路偶发性拥堵的传播和消散规律研究有实际的应用价值，为交通管理部门在车流密集区域（如：城市主干道、入口匝道及车道合流处等）的科学管理提供了参考依据。

（

）：

［1］ 张敖木翰.突发事件下非重复性交通拥堵传播规律与控制策略研究［D］.北京：北京交通大学，2012.（ZHANG Aomuhan.Studies on properties and con－trol strategies of incident－based non－recurrent traffic congestion propagation［D］.Beijing：Beijing Jiaotong University，2012.（in Chinese））

［2］ 龙建成.城市道路交通拥堵传播规律及消散控制策略研究［D］.北京：北京交通大学，2009.（LONG Jiancheng.Studies on congestion propagation properties and dissipation control strategies of urban road traffic［D］.Beijing：Beijing Jiaotong University，2009.（in Chinese））

［3］ 张敖木翰，高自友，任华玲.突发事故下交通拥堵控制策略［J］.中国科学：技术科学，2011，41（7）：955－961.（ZHANG Aomuhan，GAO Zi－you，REN Hualing.Incident－based traffic congestion control strategies［J］.Science China：Technology Science，2011，41（7）：955－961.（in Chinese））

［4］ Cremer M，Ludwig J.A fast simulation model for traffic flow on the basis of Boolean operations［J］.Mathematics and Computers in Stimulation，1986，28（4）：297－303.

［5］ Nagel K，Schreckenberg M.A cellular automation model for freeway traffic［J］.Physique I France（S1155－4304），1992，2（12）：2221－2229.

［6］ 王永明.非常态事件影响下的交通组织规划及交通流模拟研究［D］.北京：北京交通大学，2009.（WANG Yong－ming.Studies on traffic organization planning and traffic flow simulation under the influence of major public emergencies［D］.Beijing：Beijing Jiaotong University，2009.（in Chinese））

［7］ Newell G F.A simplified theory of kinematic waves in highway traffic，Part I：General theory［J］.Transportation Research Part B，1993，27（4）：281－297.

［8］ Debashish C，Dietrich E W.Practical hopping models for two－lane traffics with two kinds of vehicles：Effects of lane－changing rules［J］.Physical A（S0378－4371），1997，235（3）：417－439.

［9］ 王永明.基于元胞自动机的道路交通堵塞仿真研究［J］.系 统 仿 真 学 报，2010，22（9）：2149－2154.（WANG Yong－ming.Study on the traffic congestion's simulation based on the cellular automa－ton model［J］.Journal of System Simulation，2010，22（9）：2149－2154.（in Chinese））

［10］ 罗钧.短时交通事件干扰下的交通流仿真研究［D］.广州：华南理工大学，2012.（LUO Jun.Research on the traffic flow simulation with the disturbance of short－term traffic incidents［D］.Guangzhou：South China University of Technology，2012.（in Chinese））

［11］ 张水潮，任刚，王炜.面向交通规划的城市道路交通拥堵度分析模型［J］.吉林大学学报：工学版，2009，39（2）：111－115.（ZHANG Shui－chao，REN Gang，WANG Wei.Model of urban road traffic congestion degree analysis of traffic planning［J］.Journal of Jilin University：Engineering and Technology Edition，2009，39（2）：111－115.（in Chinese））

［12］ 贾斌，高自友，李克平，等.基于元胞自动机的交通系统建模与模拟［M］.北京：科学出版社，2007.（JIA Bin，GAO Zi－you，LI Ke－ping.Modeling and simulation of the traffic system based on the cellular automaton［M］.Beijing：Science Press，2007.（in Chinese））

［13］ 王宏.基于元胞自动机的交通流仿真及其与信号预测控制相结合的研究［D］.北京：北京交通大学，2009.（WANG Hong.Based on cellular automata simulation of traffic flow predictive control with the combination of research and its signal［D］.Beijing：Beijing Jiaotong University，2009.（in Chinese））

［14］ 商蕾.城市道路交通流仿真系统研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（3）：587－590.（SHANG Lei.Research of the urban traffic simulation system［J］.Journal of Wuhan University of Technology：Transportation Science ＆ Engineering，2010，34（3）：587－590.（in Chinese））

［15］ 邓文，陶茂华.基于激波分析理论的交通拥堵传播和消散机理研究［J］.物流技术，2012，31（4）：71－101.（DENG Wen，TAO Mao－hua.A shock wave theory based analysis of the propagation and dissipation mechanism of the traffic congestion［J］.Logistics Technology，2012，31（4）：71－101.（in Chinese））