沙质海床形态变化对波浪变形影响的试验
汪文诚,程永舟,潘 昀,李青峰
波浪在近岸浅水沙质床面上传播时,随着水深变浅,波高增大,将使床面泥沙颗粒悬浮或推移运动,在波浪破碎时尤为突出,它将导致床面形态的变化。底床形态发生变化,形成沙纹、沙坝床面。沙纹、沙坝床面阻力的增大,引致波能损耗和波浪衰减。研究波浪传播和床面形态的相互关系对于深入分析近岸波浪变形和岸滩演变具有重要意义。
近岸波浪传播和变形研究多集中考虑建筑物、地形及海床渗透性等影响。Beji[1]等人通过实验,研究了波浪在斜坡上潜堤时沿程波高的变化,分析了波浪频谱演化特性。Smith[2]等人对波浪分别通过斜坡及在斜坡上形成沙坝时的破碎特性进行了研究,指出波浪在斜坡与形成沙坝时的破碎形态和破碎指标不尽相同。蒋昌波[3]等人基于PIV研究了波浪在斜坡平台上的传播特性,表明波浪在通过斜坡时,波形不对称性明显,波能在平台上剧烈衰减,破碎导致涡结构扩散。彭延建[4]等人建立了波浪在缓变底床上传播的数学模型,得到了变水深区域波浪速度势以及自由面的分布。刘忠波[5]等人为研究海床的渗透性对波浪传播变形的影响,将一组高阶Boussinesq水波方程拓展到可适用渗透海床的情况,讨论了方程的相速度及衰减率的精确度。Karunarathna[6]等人建立了可以分析波浪在各种渗透性海床上衰减的数学模型。Corvaro[7]等人分析了海床参数对波浪衰减的影响。Dulou[8]等人通过波浪水槽试验,研究了破碎波作用下沙坝的形成过程和沙坝对波浪传播的影响。秦崇仁[9]利用波浪水槽实验,探讨了沙纹床面摩阻引起的波高沿程衰减,并将理论成果与实验成果进行比较,得出了两者符合很好的结论。
以往文献中大多针对固定底床、防波堤及潜堤对斜坡波浪传播和变形进行研究,而对沙质动床面的研究并不多见。波浪作用下泥沙运动导致海床形态变化,而床面形态变化又会影响波浪的传播和变形。作者拟利用水槽试验模拟浅海海床进行试验,观察波浪和沙床互相作用及其对各自形态变化的影响,探讨波浪和床面互相作用变化之间的关系。
1 试验设计
1.1 试验模型
试验在长沙理工大学港航中心实验室的波浪水槽中进行,水槽壁由钢化玻璃加钢桁架结构组成,底板为混凝土防渗底板,水槽长40m、宽0.5m、深0.8m。试验系统主要由大连理工大学研制的造波控制系统、试验模型系统、加拿大RBR公司 WG-50型浪高仪数据测量与采集系统以及武汉大学开发的URI-IIU型超声三维地形仪地形测量系统4部分组成。该测试系统可以产生稳定、均匀的波浪,完成沿程典型位置浪高变化及水下地形变化等数据的测量与采集。
1.2 模型设计和试验参数
试验模型的布置如图1所示。采用中值粒径为0.47mm的原型沙铺建1∶20的斜坡海床模型。模型顶部高0.5m,水槽各处相隔,安置8个浪高仪,以采集典型位置的波高。用地形仪采集水槽沿程中心线两侧0.1m处的两断面水下地形数据,地形仪对的测量范围是1m。根据试验前率定结果,试验选取周期T同为2s,波高H 和水深h不同 的4种工况(工况1:H=7cm,h=25cm;工况2:H=8cm,h=25cm;工况3:H=7cm,h=35cm;工况4:H=8cm,h=35cm)进行分组造波,每种工况每次连续造波300个周期(约10min)后,停止。待水面平静后,再进行下一组造波。分组造波既可准确分析床面形态的变化,又可减少波浪二次反射的影响。

图1 试验模型示意(单位:m)Fig.1 The sketch of the experimental model(unit:m)
2 波浪传播与变形
波浪在斜坡上传播,水深递减,波长减小,波陡增大。当波陡增大或水深减小到一定程度时,波浪破碎。破碎后,波浪互相冲击激起水点,形成浪花。随后,波浪继续向岸侧传播,并形成新的波高。随着水深再次变浅,波浪再次破碎,直至能量全部损失掉。波浪破碎伴随水体强烈紊动,长期作用后,破碎带范围内沙粒悬浮移动并形成沙纹、沙坝和沙坑。沙纹、沙坝及沙坑将与后续的波浪互相作用,从而引起一系列自身和波浪形态的变化。
试验中观测到前5组波浪作用后,底床已形成相对稳定的沙坝。波浪在初始平斜坡上和造第5组波浪后,斜坡上不同位置波面历时曲线如图2所示。分析该两组波面历时曲线可直观反映出沙坝床面对波浪传播的影响。从图2中可以看出,坡脚前的3#浪高仪和斜坡坡脚处的4#浪高仪波浪传播受斜坡影响较小,波浪形态的变化很小,可以忽略不计。位于破碎带中6#、7#和8#浪高仪数据显示,斜坡高程越高,波高越大,同时波峰变尖,波谷坦化。8#浪高仪处波浪已经破碎,波浪卷入空气,波高骤然减小。根据初始时和造第5组波浪作用后不同位置波面线对比可知,由于波浪作用下底床上形成沙纹和沙坝,波形发生了变化,破碎带前波高有明显的减小趋势。由于床面的变形,导致破碎带移动。破碎处浪高仪因浪花溅射,引起仪器实时数据忽变。故破碎带中和破碎带后的波高时有增大、时有减小,且波谷出现明显次波。
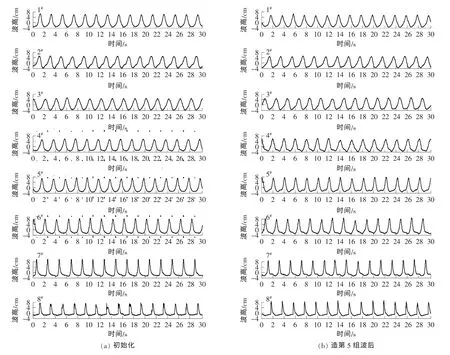
图2 不同位置波面变化(工况4)Fig.2 The wave surface elevations under different positions(case 4)
3 沙质斜坡海床上波高变化
3.1 平均波高沿程变化
工况1~4波浪作用下每组波浪的平均波高沿程变化依次如图3(a)~6(a)所示,其中平均波高为每组波浪前30个波浪波高的平均值。工况1~4波浪作用下每组波浪开始造波前破碎带处水下沙床面层形态依次如图3(b)~6(b)所示。分析该两组图,可得出每组波浪作用后波形和床面形态变化之间的关系。

图3 平均波高沿程变化及相应时刻地形变化(工况1)Fig.3 The variation of the average wave height and the charge of corresponding time topography(case 1)
图3 (a)中,7#浪高仪(水平位置X=22.6m)平均波高为9cm,随之骤减,波浪破碎在7#浪高仪位置附近。经第1组波和第6组波作用后,平均波高无明显变化。这表明此时波浪形态受床面形态变化影响较小。
图4(a)中,6#浪高仪(水平位置X =21.8m)平均波高达到11cm,随之骤减,其波浪破碎位置相对于图3(a)的提前了,在6#浪高仪位置附近。6#~8#浪高仪处平均波高随波浪作用组次的增加而逐渐发生变化。这表明此时波浪形态受床面形态变化的影响较大。
分析波高变化的原因有:工况1的波高和水深较小,波能较弱,对沙床形态的改变较慢。在经第5组波浪作用后,沙床才形成明显的沙纹,且尺寸和规模都较小,对波浪传播不产生阻力,平均波高无变化,波浪形态保持不变。工况2在第2组波浪作用后就形成较大规模的沙坝和沙坑,破碎带附近平均波高在沙床形态变化后开始减小。
图5(a)中,7#浪高仪 (水平位置X=22.6m)平均波高达到10cm,随之骤减,波浪破碎在7#浪高仪位置附近;图6(a)中,7#浪高仪处平均波高达到11cm后波浪发生破碎。图5和图6均显示平均波高随着沙床床面形态的变化而变化,破碎带范围变大,破碎位置不固定。图5中沙床床面在第2组波浪的作用后形成稳定的沙坝,破碎前平均波高有减小的趋势,最大平均波高发生处向岸侧偏移,即破碎带位置向岸侧移动。图6中沙床床面在第1组波浪作用后就形成了一定规模的沙坝,随着波浪作用组次的增加,周期性地出现沙坝、沙坑,破碎带前、后平均波高将出现剧烈无规律的变化。
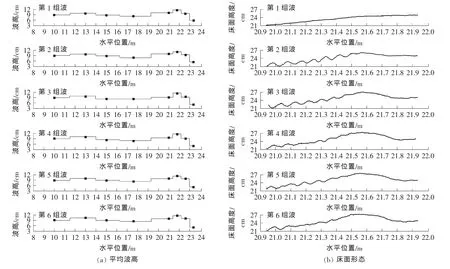
图4 平均波高沿程变化及相应时刻地形变化(工况2)Fig.4 The variation of the average wave height and the change of corresponding time topography(case 2)

图5 平均波高沿程变化及相应时刻地形变化(工况3)Fig.5 The variation of the average wave height and the change of corresponding time topography(case 3)
分析结果表明,波浪形态变化受沙纹和小型沙坝的影响较小,受一定规模且稳定的沙坝影响较大。这是由于大型沙坝有等同于潜堤的效应,使得波浪能量减小,平均波高在破碎前逐渐减小,最大平均波高发生的位置向岸侧偏移。当波高和水深均较大的波浪在斜坡海床上传播时,波能巨大,对底床冲刷剧烈,短时间内会破坏床面并周期性地形成沙坑、沙坝,同时改变波浪形态和波浪破碎位置。波浪形态和沙床床面形态是互相作用、互相影响的。

图6 平均波高沿程变化及相应时刻地形变化(工况4)Fig.6 The variation of the average wave height and the change of corresponding time topography(case 4)
3.2 波高变化率和沙坝高宽比
为进一步揭示平均波高与沙床床面形态相互变化之间的关系,作者拟通过定义参数的方法,寻找两者之间变化的规律。定义波高变化率为K1,典型沙坝(一个工况中破碎带处较大型沙坝)高宽比为K2,用公式表示为:


式中:H1为波浪在斜坡上传播时任意位置处的平均波高;H入为深水平均波高(1#浪高仪处平均波高);l沙坝和h沙坝分别为波浪作用后沙床床面形成沙坝的长度和高度。

图7 相对波高变化率K1和沙坝高宽比K2历时变化Fig.7 The relatively wave height variation rate K1and the ratio of sandbar aspect ratio changes with time
根据公式分别计算本试验各工况中的K1和K2,K1和K2历时变化如图7所示。从图7中可以看出,在水深为25cm时,K1增大,K2亦增大;在水深为35cm时,K1减小,K2亦减小。这表明相对波高变化率和沙坝的规模成正比关系。
4 结语
利用水槽试验模拟1∶20坡度浅海海床上的波浪传播,得到了波浪和沙床床面形态互相作用变化规律:
1)波浪在浅海传播至岸侧,沿程斜坡高程逐渐增大,水深变浅,波高增大,同时波峰变尖,波谷坦化,破碎后波浪有明显次波产生,波浪形态紊乱,不对称性加剧。
2)波浪形态变化受沙纹和小型沙坝的影响较小,受一定规模且稳定的沙坝影响较大。这是由于大型沙坝有等同于潜堤的效应,使得波浪能量减小,平均波高在破碎前逐渐减小,最大平均波高发生的位置向岸侧偏移。当波高和水深均较大的波浪在斜坡海床上传播时,由于波能巨大,对底床冲刷剧烈,短时间内破坏床面并周期性形成沙坑、沙坝,同时改变了波浪形态和波浪破碎位置。波浪形态和沙床床面形态是互相作用、互相影响的。
3)不同波浪条件下,相对波高变化率和沙坝的规模成正比关系。
(
):
[1] Beji S,Battjes J A.Experimental investigation of wave propagation over a bar[J].Coastal Engineering,1993,19(1-2):151-162.
[2] Smith E R,Kraus N C.Laboratory study of wave breaking over bars and artificial reefs[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1991,117(4):307-325.
[3] 蒋昌波,张陈浩,姚宇,等.斜坡平台上波浪破碎变形PIV试验研究[J].水动力学研究和进展,2012,27(4):417-423.(JIANG Chan-bo,ZHANG Chenhao,YAO Yu,et al.Laboratory study of wave transformation and breaking over a sloping platform using the PIV technology[J].Chinese Journal of Hydrodynamics,2012,27(4):417-423.(in Chinese))
[4] 彭延建,刘应中,时钟.波浪在缓变海底上传播的一个简单数学模型[J].海洋通报,2010,29(3):302-309.(PENG Yan-jian,LIU Ying-zhong,SHI Zhong.A simple mathematical model for the wave propagation over a gently sloping sea bottom[J].Marine Science Bulletin,2010,29(3):302-309.(in Chinese))
[5] 刘忠波,孙昭晨,房克照.波浪在渗透海床上传播的数学模型及其验证[J].大连理工大学学报,2013,53(3):417-422.(LIU Zhong-bo,SUN Zhao-chen,FANG Ke-zhao.Mathematical model for the wave propagation over a porous seabed and its numerical validation[J].Journal of Dalian University of Technology,2013,53(3):417-422.(in Chinese))
[6] Karunarathna S A S A,Lin P Z.Numerical simulation of wave damping over porous seabeds[J].Coastal Engineering,2006,53:845-855.
[7] Corvaro S,Mancinelli A,Brocchini M,et al.On the wave damping due to a permeable seabed[J].Coastal Engineering,2010,57:1029-1041.
[8] Dulou C,Belzons M,Rey V.Bar formation under breaking wave conditions:A laboratory study[J].Journal of Coastal Research,2002,18(4):802-809.
[9] 秦崇仁.沙纹床面摩阻引起的波高沿程衰减[J].海洋学报,1993,15(2):97-107.(QIN Cong-ren.Wave damping induced by bottom friction on ripple beds[J].Acta Oceanologica Sinica,1993,15(2):97-107.(in Chinese))

