基于桥面不平整度大跨度斜拉桥的货车行车舒适性

刘 扬，赵 鹃，殷新锋

随着经济的快速发展，交通事业也在快速发展，汽车行驶在道路和桥梁上的安全性要求是毋容置疑的，同时行车舒适性也越来越受到人们的关注。汽车行驶在桥梁上发生振动的影响因素有很多：桥面的不平整度、汽车发动机的振动、移动荷载激励下桥梁发生的振动反作用于汽车。斜拉桥作为一种相对比较柔性的结构，其振动效应相对其他桥型会更加明显，而现在的桥梁动力学研究主要集中在车桥耦合振动下的冲击系数分析以及桥梁振动响应（跨中挠度和加速度等）分析，而以行车舒适性为研究对象相对较少。

Reiher［1］最早对人体在车桥耦合作用下行车舒适进行了研究，将舒适度分为6种不同的忍受状态，迄今为止还在使用；根据实验［1］，对人体的振动影响进行了频率（0～100Hz）范围划分，为后续对ISO2631标准的制定提供了理论依据，唐传茵［2］等人采用遗传算法神经网络与神经网络辨识算法，对汽车振动舒适性进行了研究；胡振东［3］等人采用简支梁作为分析模型，得出车速以及垂向加速度对于行车舒适性影响的结论；殷新锋［4］对高墩连续梁桥进行了行车舒适性的分析；李江龙［5］等人运用自编的车桥耦合振动程序，得出了随机路面不平整度是影响斜拉桥行车舒适性主要因素的结论。行车振动舒适性是乘客人员在汽车行驶过程中对振动忍受程度的一种综合度量指标。根据ISO2631标准，提出了3种限度：承受限度、工作降低限度以及舒适度下限度。作者拟采用舒适度下限度的方法，通过其挠度限值、加权加速度均方根以及其振动频率的方式，来综合评价汽车行驶桥梁上的行车舒适性。

1 车－桥耦合系统动力分析理论

1.1 车辆模型的选定

车辆运动方程分为1／4车辆模型运动方程，1／2车辆模型运动方程以及三维车辆模型运动方程。本研究采用三维车辆模型，其正视图如图1所示和侧视图如图2所示。其中整车的自由度为：车体3自由度分别为点头转动θt、侧翻转动Φt以及车体质心竖向位移yt；车轮4自由度分别为前、后轮的翻滚转动Φ1a和Φ2a，以及前、后轮的竖向位移y1a和y2a。在计算车体横向和纵向加速度时，用桥梁结构相应的振动加速度进行替代。

图1 三维车辆模型正视图Fig.1 Front view of the three－dimensional model of vehicles

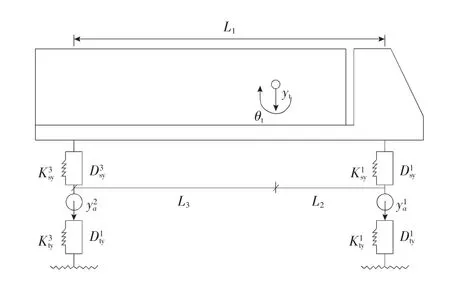
图2 三维车辆模型侧视图Fig.2 Side view of the three－dimensional model of vehicles

另外，分析车－桥耦合振动时，要对车体和行驶速度进行假设：①车体是刚体，在行驶过程中忽略车体发生相对变形；②车辆沿着某一车道直线匀速行驶，不发生变道、刹车或加减速的现象；③车轮与地面进行点接触简化，车轮与地面不发生相对滑动和脱离的现象。

1.2 车桥耦合运动方程的建立

车辆运动微分方程：

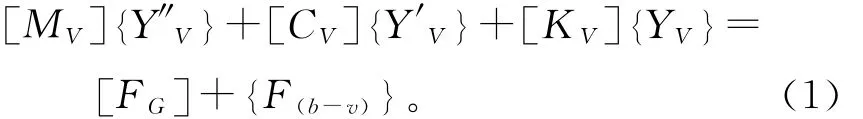
桥梁运动微分方程：

式中：［MV］，［Mb］分别为车辆和桥梁的质量矩阵；［CV］，［Cb］分别为车辆和桥梁阻尼矩阵；［KV］，［Kb］分别为车辆和桥梁的刚度矩阵；｛Yv｝，｛Yb｝分 别 为 车 辆 和 桥 梁 的 位 移 向 量；｛Fv－b｝，｛Fb－v｝分别为车辆和桥梁的相互作用力。

根据车轮与桥梁这两个系统在接触点的位移协调和作用力平衡关系，可得：

式（1）～ （4）为车桥耦合振动系统的方程组。

2 桥面不平整度的分类

桥面不平整度对车桥振动的影响比较大，尤其是对车辆行驶在桥梁上的行车舒适性，故有必要将之考虑进去；最早开始，对路面不平整度采用三角函数模拟，之后，随着研究的深入，采用功率谱密度函数模拟。现在有两种不同的表示方法：国际标准组织化协会（ISO）制定的ISO SC2／WG4国际标准［6］见表1以及中国标准局发布的GB／T 7031－86标准［7］见表2。本研究采用中国标准局发布的标准。

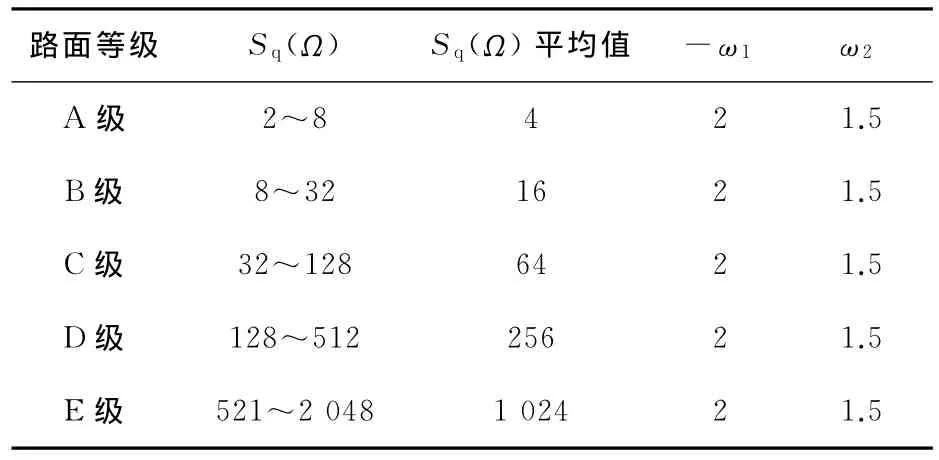
表1 国际化标准Table 1 International standards

式中：等级A～E级分别路面状况由良好～较差的划分；Ω0为空间频率的标准值，Ω0＝0.16cycle／m；Sq（Ω）为路面功率谱密度，m／cycle；ωθ（θ＝1，2）为路面不平整度频率指数。

表2 中国标准Table 2 China standards

式中：n为空间频率，n0＝0.1m－1是标准空间频率；Gq（n0）为路面不平度系数；θi为0～2π之间均匀分布的随机数。

3 行车舒适性的评价标准

在桥面不平整度的激励下，车体会产生3个方向的加速度：纵向加速度、横向加速度以及竖向加速度；同时也会产生一定的振幅和频率。本研究以ISO263－1［8］为评价标准，以车辆加权加速度均方值作为行车舒适性的定量判断依据，其行车舒适性与加速度均方值的关系见表3。

表3 ISO263－1行车舒适性标准Table 3 Standards of ISO263－1driving comfortness

其中“人体振动测量仪”采用加权振级Law。

式中：a0为加权加速度参考值，a0＝10－6m／s2。

式中：awi分别为纵向、横向及竖向加权加速度历程值，i＝x，y，z；T 为振动统计时间，取120s。

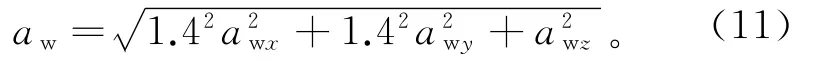
4 大跨度斜拉桥的舒适性研究

4.1 桥梁模型与车辆参数的选定

以四川省泸州市某特大斜拉桥作为研究对象，运用Midas civil建立了有限元模型，其主跨为420m预应力混凝土双塔斜拉桥，双塔双索面、密索、对称扇形布置，索塔高为146.3m。其桥梁模型如图3所示，桥梁模态分析前10阶的频率和阵型描述见表4。接着运用空间模型以及课题组研究编制的车桥耦合软件，分别从车速、车重以及桥面不平整度这3个方面对行车舒适性进行研究，同时比较其对行车舒适性影响的差异。

图3 康博大桥的桥梁模型Fig.3 Model of Kangbo bridge

表4 桥梁模态参数Table 4 Parameters of the bridge model

由于车辆过桥具有较大的随机性［9］，其中包括车型、车距、车重及车速等，根据已有对该桥的随机车流统计［10］，C1车型和C5车型的占有率分别为33.16%和22.95%，选用车辆型号为C5车型，其参数选用20t的双轴货车参数：Mt1为16 000kg，Mt2为0kg，Izt为172 160kg·m2，Ixt为61 496kg·m2，Ma1为1 415kg，Ma2为2 834kg，Ixa1为2 260kg·m2，Ixa2为2 260kg·m2，Ksy1为242 604N／m，Ksy2为1 903 172N／m，Dsy1为2 190N·s／m，Dsy2为7 882N·s／m，L1为4.85m，L2为3.73m，L3为1.12m，S1为2.4m。

4.2 桥梁模型与车辆参数的选定

车速和桥面不平整度是影响车桥振动的重要因素。以20t两轴货车为例，分别采用常见不同的路面等级A，B和C，以常见速度（60，80，100及120km／h）通过该桥梁，得到相应的各向加速度时程图。车速在60km／h且路面等级B级的竖向、横向及纵向的时程分别如图4～6所示。其中在自编程序里设置车辆起步于振动桥梁前端头的200m处，从图4～6中可以发现，在t＝0s（车体发动的时刻）至t＝12s（车体驶入桥梁的时刻）这个时间段内，相对车辆振动加速度比较小，车体处于一个稳定状态；而当车辆驶入桥梁之上瞬时，各向加速度明显增大，出现了较多的波峰。参照这些时程导出的数据，计算出其相对应的加权加速度。运用行车舒适性标准，评价不同路面平整度在不同车速下的行车舒适性，见表5。

图4 车体竖向加速度Fig.4 The vertical acceleration of the vehicle body

图5 车体横向加速度Fig.5 The lateral acceleration of the vehicle body

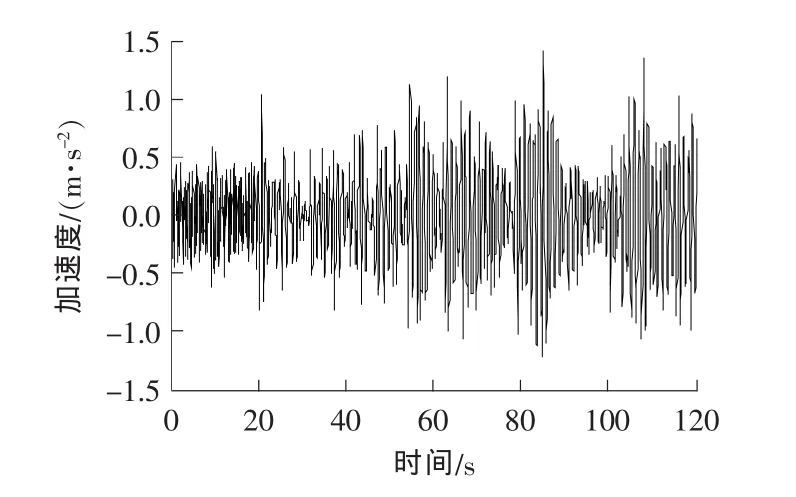
图6 车体纵向加速度Fig.6 The longitudinal acceleration of the vehicle body

从表5中可以看出，车辆随着车速以及桥面不平整度等级的提高，车体的各向（纵向、横向以及竖向）加速度相应地变大，行车舒适性也随之变差；在同一等级桥面不平整度下，车体加速度随速度的提高而增大，其中纵向加速度和横向加速度相对于竖向加速度的变化较为突出，这是由于斜拉桥在纵向和横向均有相应的约束，致使车辆振动激励在相应的方向进行衰减，而在竖向没约束，故其加速度的变化较大；在同一速度下，随着路面状况等级的降低，加速度加权均方值的变化增大，行车舒适性也越来越不舒服。

表5 不同速度与路面等级下的行车舒适性Table 5 Driving comfortness under different speeds and road surfaces

4.3 不同车重的行车舒适性

车重是影响车桥耦合振动的重要因素。根据自编程序得到车体加权加速度，采用5种（8，12，16，20和24t）不同车重的货车在常见B级路面等级以80km／h通过该桥梁。通过分析其各向加速度时程图，得到不同车重下加权加速度均方值与行车舒适性的关系，见表6。从表6中可以看出，随着车重的增加，加权加速度均方值变大，舒适性等级都保持在第2等级。

表6 不同车重下的行车舒适性Table 6 Driving comfortness under different vehicle weight

4.4 良好行车舒适性下的建议车速

桥面不平整度和车速是影响行车舒适性的重要因素。基于行车舒适性，对不同路面状况的行车速度进行分类，为良好行车舒适性的车辆速度提供相对应的范围。选用常见不同路面等级（A，B和C路面）以及不同速度下车体相对应振动加权加速度的离散点在origin中拟合成曲线（如图7所示），其中路面等级取几何平均数，求解良好行车舒适性临界速度的流程如图8所示。

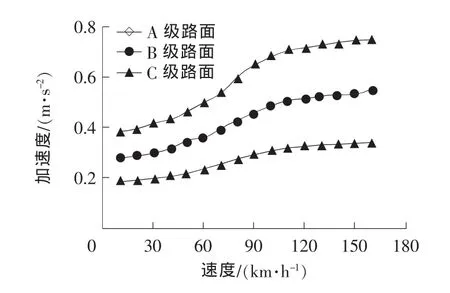
图7 车体振动加权加速度与速度的关系Fig.7 Diagram of the body vibration weighted acceleration and velocity

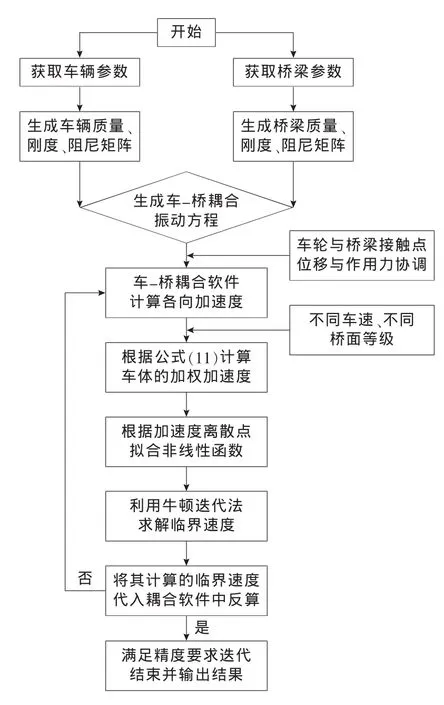
图8 临界速度的求解流程Fig.8 The flowchart of solving the critical speed

根据图7，分别拟合出不同路面等级下的非线性函数［11－12］，选用常见路面等级 A，B和 C 3级的功率谱密度输入，以ISO263行车舒适性加权加速度均方值0.5m／s2为上限标准，计算出其相对应的速度界限值，以满足第2等级行车舒适性的要求。良好行车舒适性的临界速度见表7。

表7 不同路面下的临界速度Table 7 Critical speed on different roads

根据表7可知，随着路面等级的降低，第2等级舒适性的临界速度从A级路面的∞km／h变到B级路面的107.45km／h和C级路面的61.82 km／h，变化率到达100%以上，故路面等级是影响行车舒适性的重要因素。从拟合函数可以得到：

式中：x为速度变量；y为振动加权加速度函数变量；a为函数拐点，所对应的车速常量。

根据式（12）可知，对于同一路面等级下的车体，车体振动加权加速度与速度呈现非线性关系。由该拟合函数的凹凸性可以得到，车体振动加权加速度增加显示出先急后缓的变化规律，当速度达到Va（即拟合函数的拐点）时，影响行车舒适性的主要因素是桥面等级。因此，想要保障交通安全和提高服务水平，有必要对桥面进行定期的维护。

5 结论

根据有限元软件midas，计算出斜拉桥的振型和频率。结合移动车辆作用下的整车模型编制而成的车桥耦合软件，计算在不同路面等级和不同速度车辆的竖向、横向以及纵向加速度时程图，以ISO2631为标准，评价其大跨度斜拉桥的行车舒适性，同时以车体振动加权加速度0.5m／s2为上限，根据拟合的函数，给出良好行车舒适性的建议车速。

1）在同一路面等级下，随着速度的增加，车体振动加权加速度变大，行车舒适性也随之降低；在同一速度下，随着路面等级的降低，车体振动加权加速度变大，行车舒适性也随之降低；对于同一路面和同一速度下，行车舒适性随着车重的增加而降低。

2）在不同路面等级下，B和C级路面等级良好行车舒适性的建议车速分别为107.45km／h和61.82km／h以下，而A级路面等级的设计车速都满足良好行车舒适性的要求。

3）车辆高速行驶时，车速对车体振动加权加速度的影响较小。此时，影响行车舒适性的因素主要是路面状况，故想要保障交通安全和提高服务水平，有必要对桥面进行定期的维护。

（

）：

［1］ 陆伟东，刘学晨，文建国，等.基于振动舒适度的建筑物楼板设计方法［J］.南京工业大学学报：自然科学版，2008，30（1）：16－18.（LU Wei－dong，LIU Xuechen，WEN Jian－guo，et al.Floor slab design method based on the vibration comfort degree［J］.Journal of Nanjing University of Technology：Natural Science Edition，2008，30（1）：16－18.（in Chinese））

［2］ 唐传茵，张天侠，李华，等.汽车振动舒适性评价研究［J］.振 动 与 冲 击，2008，27（9）：158－166.（TANG Chuan－yin，ZHANG Tian－xia，LI Hua，et al.Evaluation of riding comfortness of a vehicle［J］.Journal of Vibration and Shock，2008，27（9）：158－166.（in Chinese））

［3］ 胡振东，王华林.高速车辆过桥时的舒适性分析［J］.振动 与 冲 击，2002，2l（4）：104－107.（HU Zhendong，WANG Hua－lin.Analysis of comfort properties for the high－speed vehicle moving over bridges［J］.Journal of Vibration and Shock，2002，2l（4）：104－107.（in Chinese））

［4］ 殷新锋.汽车荷载作用下梁式桥与斜拉桥的动态响应分析［D］.长沙：湖南大学，2010.（YIN Xin－feng.Dynamic responses of beam bridges and cable－stayed bridges under vehicular loads［D］.Changsha：Hunan University，2010.（in Chinese））

［5］ 李江龙，李岩，盛洪飞，等.基于车桥耦合振动分析的斜拉桥行车舒适性评价分析［J］.科学技术与工程，2009，9（7）：1792－1796.（LI Jiang－long，LI Yan，SHENG Hong－fei，et al.Evaluation and analysis on ride comfortness for a cable－stayed bridge based on the vehicle－bridge vibration［J］.Science Technology and Engineering，2009，9（7）：1792－1796.（in Chinese））

［6］ 冯秀丽，李晓林，杨洪扣.路面不平度与汽车速度对动态汽车衡称重的影响［J］.中国科技论文，2012，7（11）：857－861.（FENG Xiu－li，LI Xiao－lin，YANG Hong－kou.Effects of road roughness and the speed of cars on dynamic car scale weighing［J］.China Science Paper，2012，7（11）：857－861.（in Chinese））

［7］ 长春汽车研究所.GB／T 7031－86，车辆振动输入与路面平整度表示方法［S］.北京：中华人民共和国机械工 业 部，1986.（Changchun Automotive Research Instittute.GB／T 7031－86，Vehicle vibration－describing method for road surface irregularity［S］.Beijing：The People’s Republic of China Ministry of Machine Building，1986.（in Chinese））

［8］ 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB／T 13441.2－2008／ISO2631－2－2003，机械振动与冲击，人体暴露于全身振动的评价，第2部分：建筑物内的振动（1Hz～80Hz）［S］.北京：中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会，2008.（The State Administration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China，China National Standardization Management Committee.GB／T 13441.2－2008／ISO2631－2－2003，Mechanical vibration and shock，the evaluation of the human exposure to the whole－body vibration，Part2：Vibration in buildings（1Hz to 80Hz）［S］.Beijing：The State Administration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China，China National Standardization Management Committee，2008.（in Chinese））

［9］ 王达.基于有限元模型修正的大跨度悬索桥随机车流车－桥耦合振动分析［D］.西安：长安大学，2008.（WANG Da.Analysis of vehicle－bridge coupled vibration for long－span suspension bridge with finite element model updating under random traffic flowing［D］.Xi’an：Chang’an University，2008.（in Chinese））

［10］ 胡晓.随机车流作用下大跨度斜拉桥振动响应分析［D］.长沙：长沙理工大学，2013.（HU Xiao.Random traffic flow under the action of the vibration response analysis of a long－span cable－stayed bridge［D］.Changsha：Changsha University of Science ＆Technology，2013.（in Chinese））

［11］ 杨君岐.数据分析软件的开发及应用——变量间最佳拟合函数、误差分析、趋势预测系统［J］.陕西科技大学学报，2003，21（6）：118－123.（YANG Jun－qi.Application and creatiom of the data analysis software－The system of opitimal imitated function，error analysis and tendence forecasting between variables［J］.Journal of Shanxi University of Science ＆Technology，2003，21（6）：118－123.（in Chinese））

［12］ 柳辉.解非线性方程的牛顿迭代法及其应用［J］.重庆工学院学报：自然科学版，2007，21（8）：95－98.（LIU Hui.Newton iteration method for nonlinear equation solutions and its application［J］.Journal of Chongqing Institute of Technology：Natural Science Edition，2007，21（8）：95－98.（in Chinese））