网络中λ阶短路径的最小边序号法

周勤,周炳生

（1.金陵科技学院图书馆,江苏南京211169；2.南京大学信息管理学院,江苏南京210093）

求两点间最短路径是网络中最基本的问题之一,已有一些方法,如：D（Dijkstra）算法[1-2]、A*算法、SPFA算法、Floyd-Warshali算法、Johnson算法等[2].在实际中,有些求最优问题,可转化为网络中最短路径问题[3-4].在这些算法中,D算法为其代表,但这些算法只能用以求最短路径.文献[5]中,首次引入延长矩阵的概念,用来表示网络中点与点和边的关系,从而使求最短路径的延长可用点与延长矩阵的运算来表示.实际中有些求最优问题,除了要获得最优的第一方案外,还希望获得次优的第二方案、…、第λ方案.文献[6]中,首次引入λ阶短路径的概念并介绍相应的Z算法,Z算法可根据给予的λ值,获得最优的第一方案、次优的第二方案、…、第λ方案.该算法可同时处理多始点与终点,处理方法是由一点延长到相邻的所有点后才作下一步处理（参阅该文献中的例）,为横向延长,数据较多,处理不方便.文献[7]中,分析了延长产生的相关两条路径的阶的相互关系,获得λ阶短路径的构造原则,并得到λ阶短路径的D算法.算法的处理过程,用D算法生成表来表示（参阅该文献中的例）,处理也不太方便.本文采用文献[5]的延长矩阵的概念,设计了一种λ阶短路径的最小边序号算法.

1 λ阶短路径最小边序号法

连通网络G（n,m）中点的集合记为V={x1…xn},边的集合记为E={ek}={（xixj）},其中点的个数为n=│V│,边的个数为m=│E│,边的权wk（xixj）＞0,边（xixj）中xi为xj和边（xixj）的前导点,xj为xi和边（xixj）的后继点,xi的所有相邻边的集合记为Γ（xi）.从xi不断沿相邻边延长到xj的点序列xi…xk…xj中,除了xj=xi外,其他点都不相同的序列为回路,而没有相同点则为xi到xj的路径,其他情况则为通路.路径中边的个数为路径的长度,路径的长度≤n-1.xi到xj的路径中所有边的权wk（xixj）的和为该路径的权W.

定义1 xi的相邻边集合Γ（xi）中,边按权值从小到大排序的集合称为有序边集合Γyx（xi）,即Γyx（xi）={ttxj/wk（xixj）│tt=1到│Γ（xi）│,（xixj）∈Γ（xi）},其中tt为边（xixj）的权wk（xixj）在Γ（xi）中排序的序号,权值相同的边序号相连.

定义2 Eyx为Γ（n,m）的有序边延长矩阵

其中Eyx中的项：当边（xixj）属于Γyx（xi）时有ttxj/wk（xixj）,当边（xixj）不属于Γyx（xi）时ttxj/wk（xixj）为空白.Eyx中项显示tt的称为显式有序边延长矩阵.序号tt可省去,而由矩阵的列数来表示,称Eyx中项没有显示tt的为隐式有序边延长矩阵.

连通网络G（n,m）中任两点都存在路径,从xi开始可以不断和有序边延长矩阵Eyx进行延长运算,延长到xj的序列为xi…ttxk/wk（xixk）…xj或xi…xk/wk（xixk）…xj.

定义3称路径序列xi…ttxk/wk（xixk）…xj为xi到xj的显式有序边点序列.xi…ttxk/wk（xixk）…xj为xi到xj的隐式有序边点序列.

序列xi…ttxk/wk（xixk）…xj中,项ttxk/wk（xixk）之间可用空格分开,以便识别,但通常用点序列L=xi…xk…xj/W来表示即可,其中W为点序列L的权.

定义4当点序列L=xi…xk…xj/W为路径,而xj为所求终点时,则L为结果路径.

xi到xj路径中相邻两点是由边的前导点和后继点构成的.网络中任意1条路径最大长度≤n-1,从xi最多可延长n-1次.当点序列L为通路、回路、结果路径时,再延长也不能构成新的路径,便可结束该点序列L的延长.根据文献[5],点序列L=xi…xk…xk/W与有序边延长矩阵Eyx进行延长运算L○+Eyx,是从Eyx的xk行的列中取出所有分别相关的点添加到L末,而获得新的L矩阵.而这里使用的最小边序号延长法,每次只选择有序边延长矩阵中一条可用的序号最小的边进行延长.这样获得的新L矩阵中只有1条点序列L,该点序列L其实是在原L的末点添加Eyx中1个相关的点.所以,这里L与有序边延长矩阵Eyx进行的延长运算L○+Eyx,可直接用“在L的末点添加有序边延长矩阵Eyx中相关的1个点”来表示延长运算过程.

这样,求始点xi的点序列L的最小边序号延长法是：从L=xi开始（即xi为始点）,每次选L末点为行,而相应Eyx中列为序号1的边延长.当点序列L为通路、回路、结果路径（结果路径需另外保存）时,则后退到刚延长边的前导点,即删除点序列L的末点,如刚后退获得的新L仍不能延长,则继续后退.后退后L首先选比该末点已选边序号大1的边延长,以后仍选序号为1的边延长.如此反复这些操作,直到点序列L中只有唯一点xi,有序边延长矩阵Eyx中xi行又没有可用以延长的边,便结束操作.

上述最小边序号延长法,保证xi到xj的所有结果路径都被选过1次,从而获得所有结果路径.因为,如结果路径L0未被选到过,被选过的结果路径中一定有一条与L0路径相比,这两条路径中,从xi开始一定具有一段相同点的点序列（因至少xi相同）,而该段点序列末点的后一个点一定不同（否则两条路径一样）,这表明这里的边有不同的边序号,如该处L0比该路径的边序号大,则L0在该路径以后应被选；如L0比该路径的边序号小,则L0应在该路径以前被选.否则与选法矛盾,故L0亦在结果路径中.

定义5 xi到xj的所有路径按路径权的大小排序,序号为λ的路径称为λ阶路径.规定λ=1为最短路径,λ=2为次短路径,其他类推.

在求xi到xj的λ阶短路径中,只要求1到λ阶的短路径,不必一定求出所有路径.

定义6令P为存1到λ阶的短路径的集合.B为存1到λ阶的短路径权的集合,即B={w（k）│k=1…λ}.令 B 中最大权 Mw=max{w（k）│k=1…λ},B 中最小权 mw=min{w（k）│k=1…λ}.

在求xi到xj的λ阶短路径中,当│B│=λ时,如正在延长的路径的权值已大于Mw值再延长,获得的新路径的权值将更大于Mw值,故这样的路径不需要再延长.

定义7当│B│=λ时,点序列L为路径且L的权≥Mw,则L为无效路径.

定义8 Eyx中可以被选用的边为显性边,不可以被选用的边为隐性边.

定义9删除点序列末点的操作为后退.

定义10点序列延长后增加的点为新延长点.后退操作后点序列的末点为后退延长点.

因此,点序列L的延长操作,即为在L末添点.而L的后退操作,即为在点序列L末删除点.

根据前面的最小边序号延长法,可获得下面的λ阶短路径的最小边序号法.

（1）初值：

令 L=xi,始点 xi为新延长点,P=｛｝,B=｛｝,Mw=0,mw=0,Eyx中边为显性边.给 λ 值（λ≥1）.

（2）每次获得的点序列L的处理：

①若为通路、回路,则点序列L后退.

②若为路径,求路径的权值W：

a.如为结果路径,当│B│小于λ时,则将路径权值W存入B,结果路径存入P,计算Mw和mw,点序列后退.

b.如为结果路径,当│B│=λ时,而路径权值W大于Mw,则路径为无效路径,点序列L后退.

c.如为结果路径,当│B│=λ时,而路径权值W∈B,则将结果路径存入P,点序列L后退.

d.如为结果路径,当│B│=λ时,而路径权值W小于Mw且W不属于B,则将结果路径存入P,权值W存入B,删除P中最大权值的结果路径,删除B中最大值和计算新Mw和mw,点序列L后退.

e.如不为结果路径,当│B│小于λ时,则点序列L的最后点为新延长点,点序列L继续延长.

f.如不为结果路径,当│B│=λ时,而权值W≥Mw,则路径为无效路径,点序列L后退.

g.如不为结果路径,当│B│=λ时,权值W小于Mw,则点序列L的最后点为新延长点,点序列L继续延长.

（3）后退操作后的处理：

①如后退后xi为点序列L中唯一的点,且xi的所有相邻边均为隐性边,则结束处理.

②如后退后序列L的最后点不为始点xi,若其所有相邻边均为隐性边,则该点的相邻边变为显性边,继续后退.

③如后退后序列L的末点不为始点xi,若其所有相邻边有显性边,则序列L的最后点为后退延长点,继续延长.

（4）延长的方法：

①新延长点：每次选Eyx中该点行的相应第1列的边（即序号为1边）延长（因均为显性边）,延长后该边为隐性边.

②后退延长点：每次选Eyx中该点行的相应列的序号最小的显性边（即比隐性边序号再大于1的边）延长.

这样,点序列L延长选边的方法：除后退后的第一次选序号增加1的边外,其他都选序号为1的边.

2 例证及讨论

2.1 例证

例：求图中x1到x5,λ=2的短路径.

解：根据上图,可获得隐式有序边延长矩阵

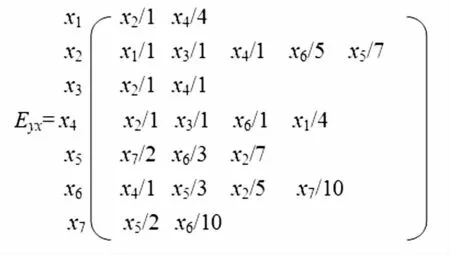
有初值：L=x1,始点 x1为新延长点,P=｛｝,B=｛｝,Mw=0,mw=0,λ=2（求最短和次短路径）.

下面L○+Eyx延长运算及获得结果L的处理,用处理过程中的部分点序列L和相应说明来表明.在点序列L处理过程中,后退操作后获得的L的末点为后退延长点,同时还表示从始点到该点为原L中需保留的那些点.被删除的点用字符加框标明,而后退延长点用下划线标明.

各处理过程说明如下：

（1）L为先取有序边延长矩阵x1行的第1列的边（x1x2）（边序号为1）延长,以后取有序边延长矩阵x2行的第1列的边（x2x1）（边序号为1）延长而得.L为回路,删除末点x1,x2为后退延长点.

（2）L为x2选有序边延长矩阵x2行第2列边（x2x3）（边序号为2的显性边）延长到x3,x3为新延长点.

（3）延长到x2后L为通路,删除末点x2,x3为后退延长点.

（4）经不断的延长和后退获得的L为x4经有序边延长矩阵x4行的第3列边（x4x6）（边序号为3）延长而得,x6为新延长点.

（5）L为通路,删除末点x4,x6为后退延长点.

（6）L 为第 1 条结果路径,存入后 P=｛x1x2x3x4x6x5/7｝,B=｛7｝,Mw=7,mw=0.删除末点 x5.

（7）L 为第 2 条结果路径,存入后 P=｛x1x2x3x4x6x5/7,x1x2x3x4x6x7x5/16｝,B=｛7,16｝,Mw=16,mw=7.删除末点 x5.

（8）L取边序号为2的边（x7x6）延长到x6后为通路,删除末点x6后,后退延长点x7因没有显性边可用以延长,删除末点x7后,x6又为后退延长点,同样因没有显性边,仍要删除末点x6,使x4为后退延长点.

（9）L为第3条结果路径,存入P且删除P中权为16的路径,有P=｛x1x2x3x4x6x5/7,x1x2x4x6x5/6｝,B=｛7,6｝,Mw=7,mw=6.删除末点x5,x6为后退延长点.

（10）因L的权为13,已大于7（Mw=7）,L为无效路径,删除末点x7,x6为后退延长点,因点x6没有显性边可用以延长,又删除末点x6,x4为后退延长点,x4选边序号为4的边（x4x1）延长到x1后为回路,删除末点x1,又因点x4没有显性边可用以延长,又删除末点x4,使x2为后退延长点.

（11）因L中只有点x1为后退延长点,又没有显性边可用以延长,所以结束处理.

最后得：P=｛x1x2x4x6x5/6,x1x2x3x4x6x5/7｝,B=｛6,7｝,Mw=7,mw=6.即：λ=1 的最短路径为 x1x2x4x6x5/6,λ=2 的次短路径为x1x2x3x4x6x5/7.

2.2 讨论

在处理过程中,处理的复杂性显然与网络的结构、相同权值的边的先后次序、始点与终点选择等有关.该算法特点为：①每次从可能的最小序号的边（即权小的边）开始延长,希望首先获得的用于参考的最大和最小权值较小.②采用无效路径和权值大的边在较后用于延长,使权值大的路径在延长中,可能因是无效路径而终止处理,从而提高效率.③每次延长和后退操作是在点序列末增加或删除一个点,点序列中其他点不动,操作简单,适用于手工和计算机处理.④可求得所有符合条件的路径.⑤如将需保存结果路径点序列的判别条件改为：回路或哈密顿回路的判别条件[8]、推销员或中国邮递员的判别条件[9],则算法将成为相应的λ阶短回路的最小边序号法.故算法具有可移植性和选择扩展功能的能力.

3 小结

本文设计的λ阶短路径的最小边序号法为纵向延长,即由一点延长到相邻的一个点后就作下一步处理,获得的数据单一、处理方便、操作简单.

[1]祝颂和,陆诗娣,陈建明,等.离散数学[M].西安：西安交通大学出版社,1991：224-228.

[2]吴华丽,吴进华,王玲玲,等.几种最短路径算法的比较[J].计算机科学,2010,37（7A）：196-197,233.

[3]施寅跃.城市道路网中蚁群最短路径算法的研究[D].南京：南京理工大学,2010.

[4]林月平,李军.最短路径算法在工程装备应急维修决策中的应用[J].科技信息,2011（13）：181.

[5]周炳生.网络中多始点与终点路径的延长算法[J].上海技术师范学院学报：自然科学版,1989（1）：32-38.

[6]周勤,周炳生.网络中短路径的Z算法[J].金陵职业大学学报,2002（1）：25-29.

[7]周勤,周炳生.网络中λ阶短路径的构造原则及算法[J].广西科学院学报,2008,24（3）：243-247,253.

[8]周炳生,周勤.λ阶短哈密顿回路的最小权法[J].广西科学院学报,2005,21（2）：67-70,75.

[9]周勤,周炳生.网络中选择路径的匹配法[J].科学研究月刊,2008（40）：93-97.