基于MATLAB的四杆／六杆颚式破碎机动态仿真

向小健，许尔威，刘浩宇

（东北大学 机械工程与自动化学院，辽宁 沈阳 110004）

0 引言

传统的颚式破碎机设计不仅周期长，且精度较低，特别是难以进行方案优化设计和比较。随着计算机技术的发展，在研究机械系统的运动规律时，借助计算机仿真技术可以大大缩短机构的设计周期，显著提高计算精度，并且还可以实现机构可视化，因此，本文利用Simulink求解机构运动约束方程，通过微积分获得最终的速度（或加速度），从而确定颚式破碎中四杆／六杆两种机构运动的位置（或速度）。

1 基于Simulink的运动学仿真

1.1 四杆／六杆破碎机机构方案简图

图1和图2分别为四杆／六杆颚式破碎机机构方案简图，其中数字代表机构各杆件标号，字母代表铰链点。

图1 四杆铰链式颚式破碎机方案简图

四杆破碎机各参数如下：其曲柄2的转速为170 r／min，lO1A＝0.04 m，lAB＝1.11 m，l1＝0.95 m，h1＝2 m，lO3B＝1.96 m，D为破碎阻力作用点，阻力始终垂直于颚板O3B，且lO3D＝0.6 m，阻力与曲柄2的角位移呈正比，当颚板4分别在左、右极限位置时，阻力分别为最大85 000 N和最小0 N。各杆的质量、转动惯量如下：m3＝200 kg，J3＝9 kg·m2，m4＝900 kg，J4＝50 kg·m2。曲柄2的质心在O1处，3，4构件质心在各构件的中心。

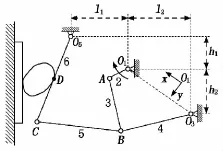
图2 六杆铰链式颚式破碎机方案简图

六杆破碎机各参数如下：其曲柄2的转速为170 r／min，lO1A＝0.1 m，lAB＝1.250 m，lO3B＝1 m，lBC＝1.15 m，lO5C＝1.96 m，l1＝1 m，l2＝0.94 m，h1＝0.85 m，h2＝1 m。各构件质量和转动惯量分别为：m3＝500 kg，J3＝25.5 kg·m2，m4＝200 kg，J4＝9 kg·m2，m5＝200 kg，J5＝9 kg·m2，m6＝900 kg，J6＝50 kg·m2。构件2的质心位于O1上，其他构件的质心均在各杆的中心处。D为破碎阻力作用点，lO5D＝0.6 m，破碎阻力的变化规律与四杆铰链式颚式破碎机相同。

1.2 四杆／六杆破碎机数学模型的建立

根据四杆颚式破碎机简图绘制出四杆机构的位移矢量图，如图3所示，其位移矢量方程如下：

其中：R1，R2，R3，R4分别为四杆机构各杆件的位移矢量。

根据六杆颚式破碎机简图绘制出六杆机构的位移矢量图，如图4所示，其位移矢量方程如下：

其中：R1，R2，R3，R4，R5，R6，L 分别为六杆机构各杆件的位移矢量。

将式（1）、式（2）、式（3）位移矢量分别投影到指定坐标系的x轴和y轴方向，建立四杆和六杆机构的位移代数方程组，对各代数方程进行两次微分计算得到各杆件加速度、角速度、角位移之间的关系方程组，再分别将四杆和六杆机构的关系方程组写成矩阵形式，分别如式（4）、式（5）所示。

图3 四杆机构的位移矢量图及角度参数

图4 六杆机构的位移矢量图 及角度参数

其中：ω2，ω3，ω4，ω5，ω6分别为对应杆件的角速度；α2，α3，α4，α5，α6分别为对应杆件的角加速度；θ2，θ3，θ4，θ5，θ6分别为对应杆件的角位移。

1.3 Simulink仿真框图的建立

根据加速度、速度、位移三者的积分关系搭建仿真框图，根据式（3）和式（4）的关系方程矩阵，编写相应的M程序。注意，用迭代法编程计算时必须知道初始条件，如曲柄的速度、加速度、角位移初值，各连杆的速度、角位移初值（为了简便计算，可以取曲柄在特殊位置时的初值），并且初值计算必须正确，否则，仿真不能进行。四杆和六杆机构的Simulink仿真框图分别见图5和图6。设置仿真时间为0.6 s，此时，曲柄运动大约为两个周期。

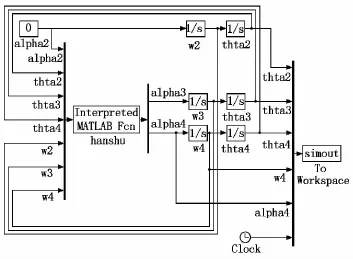
图5 四杆颚式破碎机Simulink仿真框图

2 Sim Mechanics动力学仿真

在Sim Mechanics环境中，是利用各构件之间的拓扑关系进行物理建模，它实现了构件、铰链、传感器、坐标系统等组成部分的建模和仿真，能对机构铰链约束处的受力进行求解，同时还能对机构实现实时动画显示。

根据四杆和六杆破碎机机构的拓扑关系，建立Sim Mechanics仿真模型，分别如图7和图8所示，根据杆件的质量、转动惯量、尺寸等设置模块参数（如Body的重心和端部坐标以及质量和转动惯量）。

图6 六杆颚式破碎机Simulink仿真框图

3 仿真结果及结论

运行Simulink进行各杆件角位移、角速度、角加速度仿真，输出结果到 MATLAB工作空间；运行Sim Mechanics进行各杆件角位移、角速度、角加速度以及铰链处反力和曲柄驱动力矩仿真，将反力和驱动力结果输出到MATLAB工作空间。

图9为四杆和六杆机构摆杆的角位移、角速度、角加速度曲线。由图9可知，四杆机构的摆杆角度变化范围、角速度幅值、角加速度最大值都要比六杆的小，连杆机构的整体波动性也小。

图10为四杆和六杆机构的摆杆（颚杆）铰链O3和O5处的反作用力曲线，图11为四杆和六杆机构曲柄驱动力矩曲线。通过以上比较说明：四杆机构的摆杆速度、加速度和驱动力矩的波动性以及摆杆铰链处的受力情况要好于六杆机构，四杆破碎机构的运行更平稳。

综上所述，四杆铰链式破碎机的机械性能比六杆 铰链式破碎机要好。

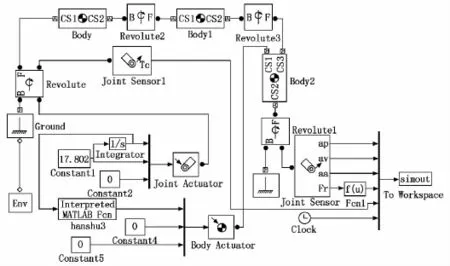
图7 四杆颚式破碎机Sim Mechanics仿真模型

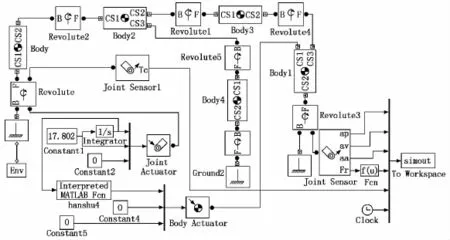
图8 六杆颚式破碎机Sim Mechanics仿真模型

图9 四杆和六杆机构摆杆的位移、速度和加速度

图10 四杆和六杆机构摆杆铰链处反力曲线

图11 四杆和六杆机构曲柄驱动力矩曲线

［1］ 窦照亮.颚式破碎机结构参数优化和破碎力仿真分析［D］.昆明：昆明理工大学，2010：1－67.

［2］ 傅彩明.新型颚式破碎机动态设计研究［D］.北京：北京科技大学，2004：1－48.

［3］ 刘菊蓉，王旭飞.偏置式曲柄滑块机构的优化设计及运动分析［J］.机械研究与应用，2005（12）：99－100.

［4］ 孔维忠，振兴.六杆机构的运动仿真及方法比较［J］.机械工程与自动化，2012（5）：67－69.

［5］ 赵晓东，刘艳娜.两足机器人的Sim Mechanics建模［J］.浙江大学学报，2010，44（7）：1361－1367.