铝板带材冷轧机压力AGC仿真对比与实验分析

安俊静，白 磊，赵春江，郝琳璐，石建辉

（1.太原科技大学 材料科学与工程学院，山西 太原 030024；2.重型机械教育部工程研究中心，山西太原 030024）

0 引言

随着社会的快速发展，工业生产中不仅对板带材的需求量在增加，更对板带材的几何尺寸精度的要求更加严格［1］。厚度精度是其最重要的品质指标之一［2］，所以对板带材的厚度自动控制系统（AGC）的研究越发重要。本文对在变刚度压力AGC（BISRAAGC）［3］、厚度计型 AGC（GM－AGC）［4］和动态设定型AGC（DAGC）［5］三种压力 AGC控制方式下的铝板带材冷轧机的AGC系统进行仿真对比，综合考虑铝板带材冷轧机现有设施的实际情况，对系统进行实验调试和研究，使自动厚度控制系统的控制精度得到一定改善，动态响应时间缩短。

1 系统组成

实验铝板带材冷轧机的AGC系统采用西门子S7－300PLC控制器，实现冷轧机主要设备的动作控制。AGC系统的执行机构包括电液伺服阀、压下伺服液压缸、位移传感器、液压泵站等。电液伺服阀的型号为FF－102／30，其额定压力为21 MPa，额定流量为30 L／min，额定电流为10 m A；压下伺服液压缸外径为330 mm，活塞杆直径为160 mm，工作行程为30 mm。

2 系统数学模型的建立

2.1 电液伺服阀的传递函数

设电液伺服阀的传递函数为G1（s），则有：

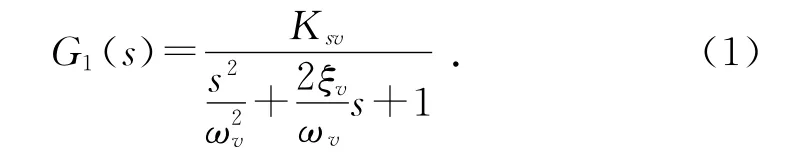
其中：ωv为伺服阀固有频率，ωv＝628 rad／s；ξv为阻尼比，ξv＝0.7；Ksv为伺服阀流量增益，Ksv＝0.070 7 m3／（s A）。将相关参数代入式（1），得：

2.2 伺服放大器的传递函数

设伺服放大器的传递函数为G2（s），则有：

其中：I为伺服放大器输出电流，I＝0.01 A；Us为输入电压，Us＝10 V。将相关参数代入式（3）得：

2.3 伺服阀控伺服液压缸的传递函数

设伺服阀控伺服液压缸的传递函数为G3（s），在质量－弹簧－阻尼系统中，由阀控液压缸的动态特征三大方程［6］得到其传递函数为：

其中：A为活塞有效作用面积，A＝0.038 0 m2；Kce为流量压力系数，Kce＝8.15×10－12m5／（Ns）；M 为冷轧机刚度值，M＝1.006×109N／m；ω0为二阶环节固有频率，ω0＝2 300 rad／s；ξ0为阻尼比，ξ0＝0.18；ψ为一阶环节转折频率，ψ＝2.84 rad／s。将所有数据代入式（5）中，得到：

2.4 位移传感器的传递函数

设位移传感器的传递函数为G4（s），则有：

其中：Uw为位移传感器输出电压，Uw＝10 V；Xp为位移传感器行程，Xp＝5×10－2m。将相关参代入式（7）得：

2.5 PID控制器的传递函数

设PID调节器的传递函数为G5（s），则有：

其中：Kp为比例系数，KI为积分系数。Kp和KI的值通过PID调节取得。

3 系统仿真与实验分析

3.1 系统仿真比较

根据AGC系统各元件的传递函数，应用MATLAB／Simulink软件分别对 BISRA－AGC，GM－AGC和DAGC模型下的系统控制过程进行仿真。图1、图2和图3分别为3种压力AGC的模拟控制模块图。

图1 BISRA－AGC模拟控制模块图

图2 GM－AGC模拟控制模块图

图3 DAGC模拟控制模块图

在开始仿真之前，根据实验系统的现有情况，设置相同的初始参数，按照以上3种控制方式分别进行模拟仿真。仿真时间为30 s，入口厚度为10 mm，轧制力为30×104N，通过前期调试确定PID参数Kp＝70、KI＝1，铝板塑性系数Q＝39.2×104N／mm。这样，当给定铝板厚度控制系统一个阶跃信号，得到了在BISRA－AGC控制、GM－AGC控制以及DAGC控制3种压力AGC控制模型下的系统仿真结果，如图4所示。

由图4可以看出：在BISRA－AGC和GM－AGC模型控制下系统的动态响应时间均为0.065 s左右，DAGC模型控制下系统的动态响应时间为0.045 s左右；当系统趋于稳定时，在三种压力AGC模型控制下，仿真厚度值均在10 mm以上，其中BISRA－AGC模型控制下的厚度正偏差约为0.6 mm，GM－AGC和DAGC模型控制下的厚度正偏差约为0.25 mm。综合比较之后得出结论：DAGC模型控制下系统的仿真效果更好，系统的动态响应时间更快，系统更稳定。

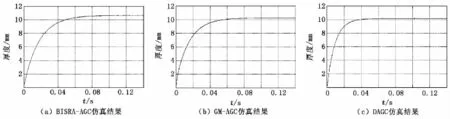
图4 3种控制模型下系统的仿真结果

3.2 轧制铝板的实验结果与分析

选取3块相同规格的铝板：长度为500 mm，宽度为200 mm，厚度大约为3.5 mm。以2 mm为间隔，在相同的板厚波动状态下进行实验，依次记录每块铝板的入口和出口厚度数据。设置相同的实验参数：初始辊缝值S0为2.00 mm，轧制力P0为4×105N，轧机刚度值M 为120×104N／mm，铝板塑性系数Q为39.2×104N／mm。

分析处理在每个控制模型下测得的实验数据，绘制出轧制3.5 mm铝板的入口厚度波动曲线，由于不同的控制模型下采用相同规格的铝板，所以入口厚度波动曲线大致相同，如图5所示。在BISRA－AGC、GM－AGC和DAGC三种控制模型下的铝板出口厚度波动对比曲线如图6所示。

图5 轧制铝板的入口厚度波动曲线

由图6可知：在BISRA－AGC控制模型下，铝板的出口厚度最大偏差为0.052mm；在GM－AGC控制模型下，铝板的出口厚度最大偏差为0.043mm；在DAGC控制模型下，铝板的出口厚度最大偏差为0.037mm。从3条曲线的波动趋势可知：DAGC控制模型下的铝板厚度波动更加趋于缓和、平稳。

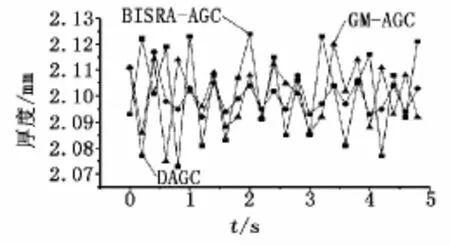
图6 3种控制模型下的铝板出口厚度波动对比曲线

4 结论

经过模拟仿真对比和实验分析得出结论：采用DAGC压力控制模型，能够以较低的成本投入，使得系统的动态响应时间得以提高，系统的控制更加稳定，控制精度大大提高，从而有效改善冷轧机的厚度自动控制效果。

［1］ 丁修堃.高精度板带钢厚度控制的理论与实践［M］.北京：冶金工业出版社，2009.

［2］ 王志霞，黄庆学，李玉贵.三种典型压力AGC的仿真研究［J］.装备制造技术，2007（5）：21－22.

［3］ E JM Geddes.Multivarable control of a high performance tandem cold rolling mill［C］／／IEEE Control Conference.［s.n.］：IEEE，1994：202－207.

［4］ Luis E Zarate.Neural networks and fuzzy rules basesd control for cold rolling process via sensitivity factors［C］／／27th Annual Conference of the IEEE Industrial Electronics Society.［s.n.］：IEEE，2001：64－69.

［5］ 张进之.动态设定型变刚度厚控方法（DAGC）推广应用［J］.冶金设备，2007（4）：1－5.

［6］ 王春行.液压控制系统［M］.北京：机械工业出版社，2011.