基于LQG理论的电子控制空气悬架控制策略研究
詹长书,孙世磊
(东北林业大学交通学院,哈尔滨150040)
悬架系统是汽车的重要组成部分之一,悬架对于汽车的行驶平顺性、乘坐舒适性、操纵稳定性起着至关重要的作用。在车辆负载相同时,空气弹簧较普通弹簧的振动频率更低[1],能够有效的提高汽车的行驶平顺性与乘坐舒适性。ECAS系统由传感器技术、控制器算法和执行机构组成。传感器技术与执行器可以在技术上解决,而控制策略是控制系统的关键部分。ECAS控制理论已经引起了国内外学者的高度重视,也取得了丰富的研究成果。例如赵丽梅提出利用模糊控制对空气悬架对车身加速度进行控制[2];王辉等设计了网络辨识器仿真并验证了神经网络自适应控制策略对电子控制空气悬架的有效性[3]。但是模糊规则表的设计比较繁琐且主观性较强。神经控制可以对权值系数进行学习训练,能够有效的适应不确定系统,但需要大量的数据进行训练。本文提出将线性二次型高斯控制理论(LQG)应用到电子控制空气悬架中,利用MATLAB/simulink仿真软件对ECAS进行了仿真研究。
1 路面输入模型的建立
路面输入模型采用滤波白噪声,其微分方程为[1]
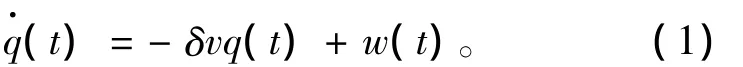
式中:q(t)为路面激励;δ为路面不平度系数,取B级路面0.1303;v为汽车运行速度,本文取50 km/h;w(t)为一路面白噪声。
2 车辆空气悬架模型的建立
当悬架质量分配系数接近1时[4],汽车前后悬架在垂直方向上的运动几乎是相互独立的。于是,可将车辆模型简化为1/4车辆的二自由度悬架系统(如图1所示)。尽管简单,但反映了汽车行驶平顺性性能分析的主要特征。电控空气悬架可等效为车身质量块与车轮质量块之间并联阻尼器、弹簧与悬架控制力的模型,将空气弹簧的作用力分解为定常刚度的弹簧力与可变悬架作用力。

图1 1/4悬架模型Fig.1 Model of quarter vehicle
取静力平衡位置为坐标原点,忽略轮胎阻尼,根据牛顿第二定律得到公式(2):

式中:m1、m2分别为车辆车身质量、轮胎质量;c为悬架阻尼系数;kt为悬架刚度系数;z1、z2、q分别为车轮垂向位移、车身垂向位移、路面输入位移;Fk为相对空气弹簧力;Ua为等效主动作用力(相当于空气弹簧气压变化引起的弹簧弹力变化量)。Fk=Fa-G,G为静载荷;Fa是与空气弹簧变形量、有效截面积、有效容积、空气弹簧内压力等相关的绝对空气弹簧力[5,9]。
最优控制器的设计以上文提出的模型作为参考模型,定常刚度的弹簧力为
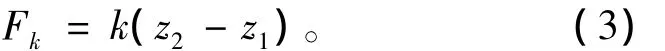
式中:k为被动空气悬架等效静刚度。
上式代入式(2)并整理可得
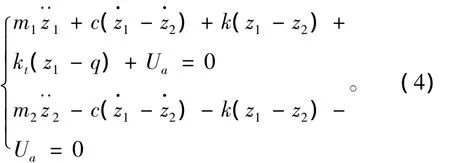
当Ua=0时,得到被动悬架的振动微分方程
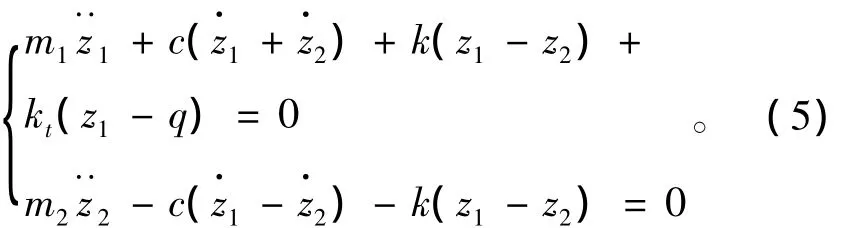

根据现代控制理论,得到空气悬架系统的状态方程和输出方程为
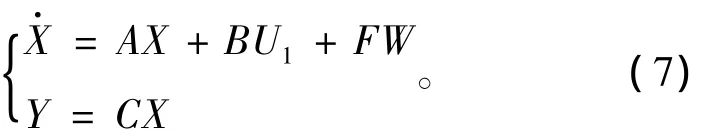
式中:C为单位矩阵。
3 控制器的设计
综合考虑悬架平顺性的评价指标:车身加速度、悬架动行程、轮胎位移。利用线性二次型高斯最优控制理论,寻求最优控制,使得下面的性能指标最小[6]
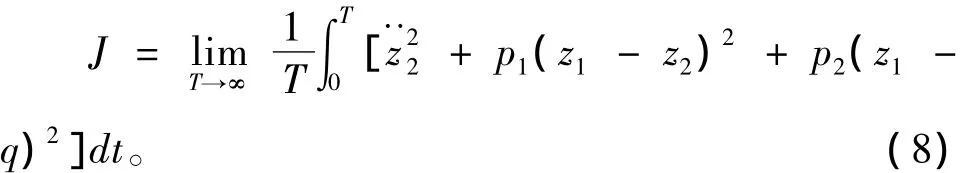

式(8)中:Q为状态变量的加权半正定矩阵;R为控制力的加权矩阵;N交叉项矩阵。
利用最小值原理求解,可归结为求解Riccati方程[7-8].利用 MATLAB中的黎卡提方程求解函数 lqr()[5],其格式[K,P,E]=LQR(A,B,Q,R,N),A,B,Q,R,N为输入矩阵。可求得最优反馈控制矩阵K。最优控制律U=-KX,即最优控制力
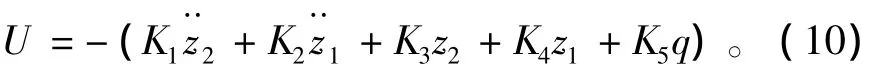

表1 系统仿真参数Tab.1 Simulation parameters
系统仿真参数见表1,代入仿真参数,解得最优反馈矩阵:

4 仿真分析
被动空气悬架系统与主动悬架系统采用相同的设计参数[10]。利用MATLAB/simulink工具箱搭建系统模型进行仿真,如图2所示。得到了仿真结果如图3~图8所示。由于车身加速度是汽车平顺性的重要评价指标,所以降低车身加速度是控制器设计主要考虑的任务之一。
表2给出了主动、被动悬架行驶平顺性的3个评价指标均方根值的性能对比。从表中可以看出当p1=20 000,p2=100时,基于LQG的主动空气悬架的车身加速度明显低于被动悬架的值,选择合适的加权值能够有效的降低汽车的车身加速度。主动悬架的动行程均方值也有一定的降低。但是主动悬架的轮胎动位移比被动悬架略有增大。

表2 性能对比Tab.2 The performance comparison
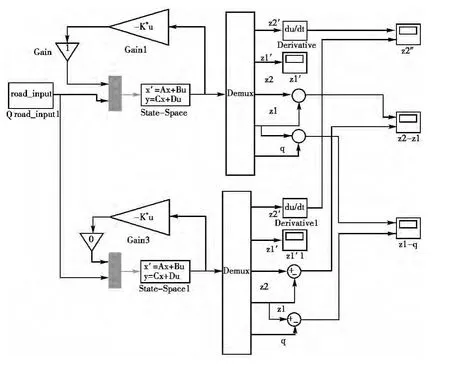
图2 悬架仿真模型Fig.2 Simulation Model of suspension

图3 被动悬架垂直加速度仿真曲线Fig.3 Simulated curves of passive suspension vertical acceleration

图4 主动悬架垂直加速度仿真曲线Fig.4 Simulated curves of active suspension vertical acceleration

图5 被动悬架动行程仿真曲线Fig.5 Simulated curves of passive suspension dynamic deflection
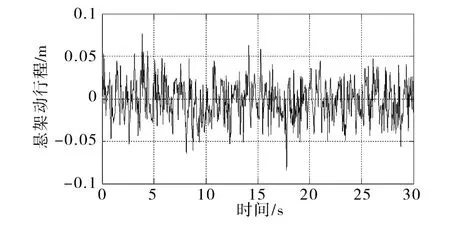
图6 主动悬架动行程仿真曲线Fig.6 Simulated curves of active suspension dynamic deflection

图7 被动悬架轮胎动行程仿真曲线Fig.7 Simulated curves of passive suspension tire dynamic deflection

图8 主动悬架轮胎动行程仿真曲线Fig.8 Simulated curves of active suspension tire dynamic deflection
5 结论
以上通过滤波白噪声作为路面激励,利用MATLAB/simulink工具箱模拟仿真了利用线性二次型高斯最优控制(LQG)在空气悬架中的动态响应。仿真结果表明,将LQG控制策略应用在空气悬架中能有效的降低汽车的车身加速度,并能在一定程度上减小悬架动行程与轮胎动行程。由于悬架的车身加速度、悬架动挠度、轮胎动位移三者之间存在一定的制约关系,当选取一定的加权系数使得某个或者某两个值明显降低时,往往导致另外的参数值升高。本文以车身加速度为主要的控制目标,使其有显著的降低。但使轮胎动位移略有增加,由于改变程度较小,对实际的轮胎行程的限值影响不大。由于实际运行中的车辆会受到多种因素的干扰,而利用软件仿真所考虑的因素有限,忽略的因素较多,会与实际状况有一定的出入。但是在一定程度上反映了利用LQG控制策略控制的空气悬架对提高车辆的乘坐舒适性有一定的效果。
[1]喻 凡,林逸编.汽车系统动力学[M].北京:机械工业出版社,2005.
[2]赵丽梅.半主动空气悬架模糊控制的仿真研究[J].汽车科技,2010(3):58-60.
[3]王 辉,朱思洪.半主动空气悬架神经网络的自适应控制[J].农业机械学报,2006(1):28-31.
[4]余志生.汽车理论[M].北京:机械工业出版社,2006.
[5]鲍卫宁.汽车空气悬架及其控制系统动力学仿真分析研究[D].武汉:华中科技大学,2011.
[6] 兰 波,喻 凡,刘娇蛟.主动悬架LQG控制器设计[J].系统仿真学报,2003(1):138-140.
[7]周 柔,郭志峰.主动悬架控制技术研究[J].计算机与现代化,2012(1):176-180.
[8] Yu F,Crolla D A.An optimal self- tuning controller for an active suspension[J].Vehicle System Dynamics,1998,29:51 -65.
[9]肖启瑞,樊明明.车辆工程仿真与分析:基于MATLAB的实现[M].北京:机械工业出版社,2012.
[10]李亮平,苏初旺,谢美芝,等.汽车电子稳定程序控制策略的研究[J].森林工程,2009,25(5):47 -50.

