航天器空间自主交会故障诊断*

刘伟杰，谌 颖

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

随着航天器交会对接任务的日益增多，尤其是空间自主交会技术的飞速发展，空间交会的安全性也成为一个普遍关注的问题［1-2］.在空间交会的最终逼近段，外部存在重力梯度等环境扰动，追踪航天器内部存在太阳能帆板的挠性运动等干扰，以及高精度的控制要求，使得这一阶段的交会操作得到了广泛的关注［3］.日本宇宙航空研究开发机构(JAXA)认为在国际空间站邻近空间的接近轨迹设计及其相对应的故障诊断、隔离与恢复(FDIR)，最终逼近段的闭环轨迹控制以及 H-转移飞行器(HTV)被国际空间站(ISS)的机械臂安全捕获是交会对接中的三大难点［4］.欧洲的自动转移飞行器(ATV)除了在最终逼近段应用导航敏感器监测追踪航天器的状态外，还监测加速度计的测量信息以及与“ISS俄罗斯对接港(DUP)”的相对状态矢量，从而达到 FDIR目的［3，5-6］.日本的 HTV 通过设计安全网(safety net)软件监测追踪航天器的姿态、加速度及轨迹等状态量［4，7］.美国的“天鹅座”在最终逼近段，除了有冗余导航敏感器进行追踪航天器的故障诊断与隔离(FDI)，还通过安全通道监视位置、速度以及计算长半轴导数等3个数据来保证追踪航天器轨迹的安全性［8］.工程上这种方法虽然简单实用，但由于航天器的推力发动机输出值可能会存在偏差，以及在外部干扰等作用下容易发生误报警，从而降低这种诊断方法的准确性.另外这种检测方法很难隔离故障，发生故障后最常见的对策就是关机进入安全轨迹或者进行避撞机动，这大幅增加了空间交会的成本.近年来故障诊断与容错技术的发展，在航空航天领域的应用越来越多［9-10］.但采用故障诊断的思路解决最终逼近段的广义FDIR问题，目前研究的较为少见.吴宏鑫等［2］采用基于系统输入输出信号处理的方法，结合Hill方程的理论解进行发动机的故障诊断研究.

基于解析模型的故障诊断方法是目前最常用的故障诊断方法之一，其理论得到了迅猛发展.Beard［11］最早提出了用解析冗余代替硬件冗余的思想，并研究了用故障检测滤波器生成FDI所需的方向性残差的方法.在空间交会过程中，考虑到故障误报及漏报的可能性，需要控制器具有一定的鲁棒性，再考虑到追踪航天器本身配置了很多的执行机构冗余和敏感器冗余，还希望控制器具有一定的容错性，至少故障发生后短时间内不会发生碰撞或者触发门限阈值.

本文设计了基于模型的未知输入鲁棒观测器以及H∞鲁棒控制器，探讨空间交会中控制器容错性的重要性，以及分析不同控制器作用下故障检测器的诊断效果，从而总结出最终逼近段故障诊断与控制器设计的研究方向.

1 未知输入观测器

假设目标飞行器在圆轨道上运动，定义目标轨道坐标系OXYZ为:O为目标飞行器质心，OZ指向地心，OX在目标飞行器轨道平面内与OZ垂直且指向前进方向，OY按右手法则确定在目标飞行器的轨道坐标系内，追踪飞行器的位置和速度分别表示为.在最终逼近段，空间交会操作往往限制于轨道平面内，追踪飞行器的运动方程由C-W方程［12］描述为

式中，ω0为目标飞行器的轨道角速度，ax'、az'为外部输入加速度.取令

此处系统只考虑执行机构故障，假定系统受加性未知输入干扰，则系统可以描述为

式中，f(t)∈Rh表示故障矢量，d(t)∈Rq表示系统的扰动矢量，y(t)∈Rm是输出矢量，R为故障分布矩阵，E表示扰动的输入系统矩阵，C表示系统的输出系数矩阵.设计基于全阶观测器的残差生成器

式中，r∈Rp是残差矢量和是状态与输出估计，K为需要设计的观测器参数，Q是残差加权因子.

式中H=QC.对故障和干扰响应的残差进行拉普拉斯变换后得到:

为了使残差r1(t)与干扰无关，必须使传递函数中所有残差与干扰有关的项设置为0［13］，即

而获得干扰解耦设计的必要条件为:QCE=HE=0.其通解为

式中，Q1∈Rp×m是任意设计的矩阵，(CE)+是矩阵CE的伪逆.如果rank(CE)=q，则有(CE)+=[(CE)T(CE])-1(CE)T.残差加权矩阵Q的行数为

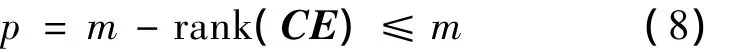
引理1［13］.如果 {C，A}能观，对于任何一组自共轭复数 λi(i=1，2，3，…，n)，总存在矩阵 K ∈ Rn×m，及非奇异矩阵L∈Cn×n，使得

式中，li=N(λi)gi，wi=M(λi)gi(i=1，2，…，n).M(s)与N(s)满足如下右互质因式分解:

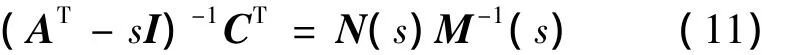
而gi是一组满足如下两个条件的参数矢量:

2)gi=gj当且仅当 λi=λj.

引理 2［14］.假定 E是列满秩的，C是行满秩的，{ C，A}能观，μ 是空间LKer(CE)的大小，且 ξi(i=1，2，…，μ )是 LKer(CE)的一组基.如果存在:①一组特征值 λi(i=1，2，…，n);②一组实数 αij，(i=1，…，p;j=1，…，μ );③一组矢量 gi∈ Cm(i=1，2，…，n).满足下列条件，那么鲁棒故障检测问题有解，并且故障观测器的加权矩阵 Q=［q1，…，qp］T(qi=αi1ξ1+αi2ξ2+αi3ξ3).

1)Re(λi)＜0，并且λi是互不相同的复数，并且两组 λi，i=1，2，…，p以及 λj(j=p+1，…，n)是自共轭复数.

4)由式(10)所给定的矩阵L非奇异.

鲁棒故障观测器的参数计算遵循以下步骤.步骤1.求解满足式(11)右互质因数分解的一对右互质多项式矩阵N(s)、M(s).

步骤2.确定LKer(CE)的大小μ.如果μ≠0，算出LKer(CE)的基 ξi(i=1，2，…，μ )，否则中止求解.

步骤 3.求解参数矢量 gi(i=1，2，…，p).gi的表达式

步骤4.本文中A∈R4×4，按照式(10)构成左特征矢量的一般形式.

步骤5.选择一组参数 λi，αij和gi(i∈p+1，…，n)，使其满足引理2的4个条件.

步骤6.将得到的λi，αij代入到步骤3中，得到gi的具体形式.

步骤7.基于前面设计的参数以及得到的gi，计算矩阵L和W，以及观测器增益矩阵K以及加权矩阵Q.

其中 N(s)、M(s)的求解采用 Duan［15］给出的方法，对于可观测矩阵对 {C，A}，取其增广矩阵，Tn通过将1的前 行进行一系列的行变换和后n+r列进行一系列的列变换，最终转换成的形式，则N(s)、M(s)的一般广义形式为

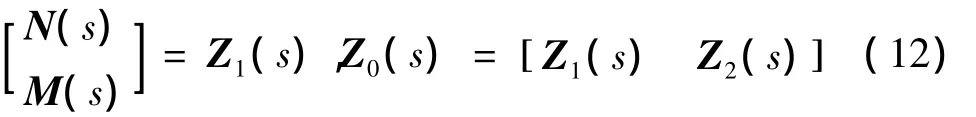
假设系统全状态可测，所以C=I.干扰只考虑地球摄动等外部干扰，取E=［0 1 0 1］T，可得p=3 .对于LKer(CE)的基可取为ξ1=［1 0 0 0］T，ξ2=［0 0 1 0］T，ξ3=［0 1 0-1］T.

对于观测器系统设计自共轭复数 λi={-1，-2，-3，-4 }，代入式(10)即可求得观测器增益

2 闭环控制器

考虑到交会过程中存在大量干扰，本文设计H∞控制器进行仿真研究，首先将系统(2)转换为广义系统的形式.

式中，z∈Rq表示系统可控输出，C1、D12表示状态和控制输入到可控输出的状态矩阵.设计状态反馈控制器

使得无故障时的闭环系统为

根据鲁棒控制理论［16］，对于系统(13)，存在状态反馈H∞控制器(14)，当且仅当存在正定矩阵X和矩阵W，使得以下不等式成立.

如果矩阵不等式(15)存在一个可行解X*、W*，则控制律为K1=W*(X*)-1.

3 仿真分析

仿真中目标航天器轨道高度400 km，初始时相对运动状态(相对位置单位m，速度单位m/s)为x0=［-50，0，0.45，0］.故障模型参数采用 ATV 推力发动机的工作参数.根据前一节中的方法，求得H∞控制律下闭环特征值为 λcl=为方便比较，引用PD控制律，控制参数为x'轴向上KPx=0.001 2，KDx=0.07，z'轴向上KPz=0.002，KDz=0.09 .

首先在没有故障发生时进行仿真，在两个轴上各用一个最大值为10-4m/s2的零均值白噪声表示外部干扰.从图1～2中可以看出，两种控制器下系统的响应曲线均十分理想，故障诊断器在两种控制器下都显示没有故障发生.

当系统发生加性故障，在z轴上170～200 s之间发动机的故障可表示为fz(t)=-0.01sin(0.2πt)m/s2，系统的仿真图如图3～4所示.

从仿真中可以看出，当故障发生后，PD控制器达不到控制的目标，追踪航天器有与目标航天器碰撞的可能，这种情况下故障诊断器的诊断效果十分理想.使用鲁棒控制器时，系统的运行轨迹没有显著变化，但故障诊断器产生的残差被大大削弱，有可能导致故障漏报，因此故障诊断器的设计与控制器的设计需要统一考虑.

图1 无故障情况下的相对位置Fig.1 Relative positions without fault

图2 无故障情况下诊断结果Fig.2 Detection results without fault

图3 故障情况下的相对位置Fig.3 Relative positions with fault

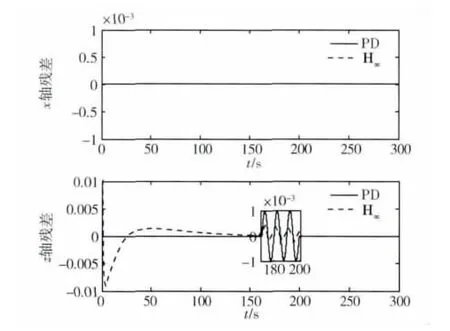
图4 故障情况下的诊断结果Fig.4 Detection results with fault

4 结论

本文针对空间交会最终逼近段的开环C-W方程，设计了基于开环模型的未知输入鲁棒故障观测器和鲁棒H∞控制器.通过对比仿真发现，系统的控制器和故障诊断器之间存在相互影响.因此，针对空间交会的最终逼近段，设计合理的控制器与故障观测器具有光明的工程前景.

［1］林来兴.四十年空间交会对接技术的发展［J］.航天器工程，2007，16(4):70-77.LIN L X.Development of space rendezvous and docking technology in past 40 years［J］.Spacecraft Engineering，2007，16(4):70-77.

［2］吴宏鑫，胡海霞，解永春，等.自主交会对接若干问题［J］.宇航学报，2003，24(2):132-143.WU H X，HU H X，XIE Y C，et al.Several questions on autonomous rendezvous docking［J］.Journal of Astronautics，2003，24(2):132-143.

［3］BOURDON J，DELPYP，GANETM，et al.Application of H∞design on ATV control loop during the rendezvous phase［C］//Proceedings of the 5thInternational ESA Conference on Spacecraft Guidance，Navigation and Control Systems.Nice，France:ESA，2002:289-296.

［4］UEDA S，KASAI T，UEMSTSU H.HTV rendezvous technique and GN＆C design evaluation based on 1st flight on-orbit operation result［R］.Washington D.C.:AIAA，2010.

［5］CAVROIS B，REYNSUD S，PERSONNE G，et al.ATV GNC and safety functions synthesis:overall design，main performances and options［R］.Washington D.C.:AIAA，2008.

［6］CAVROIS B，CHAVY S，DELPY P，et al.ATV control monitoring:adedicated ATV function to ensure the safety of the ISS during rendezvous［C］//Proceedings of the 1stIAASS Conference“Space Safety，A New Beginning”.Nice，France:ESA，2005:97-102.

［7］UEDA S，KASAI T，UEMATSU H.HTV guidance，navigation and control system design for safe robotics capture［R］.Washington D.C.:AIAA，2008.

［8］SARGENT R，MITCHELL I，BREGER L，et al.A fault management strategy for autonomous rendezvous and capture with the ISS［R］.Washington D.C.:AIAA，2011.

［9］邢琰，吴宏鑫，王晓磊，等.航天器故障诊断与容错控制技术综述［J］.宇航学报，2003，24(3):221-226.XING Y，WU H X，WANG X L，et al.Survey of fault diagnosisand fault-tolerance controltechnology for spacecraft［J］.Journal of Astronautics，2003，24(3):221-226.

［10］张森，于登云，王九龙.国外航天器故障诊断研究进展［C］//第二十届全国测试与故障诊断技术研讨会论文集.贵阳:中国计算机自动测量与控制协会，2011:1-7.

［11］BEARD R V.Failure accommodation in linear system through self reorganization［D］.San Francisco:Masschusetts Institute for Jet Engines，1975.

［12］林来兴.空间交会对接技术［M］.北京:国防工业出版社，1995:14-15.

［13］KARCANIAS N，KOUVARITAKIS B.The output zeroing problem and its relationship to the invariant zero structure［J］.International of Journal of Control，1979，30(1):395-415.

［14］CHEN J，RON J，PATTONR J.Robust model-based fault diagnosis dynamic systems［M］.Boston:Kluwer Academic Publishers，1999:94-96.

［15］DUAN G R.Solution to matrix equation AV+BW=VF and their application to eigen-structure assignment in linear systems［J］.IEEE Trans.Automat.Contr.，1993，38(2):276-280.

［16］俞立.鲁棒控制-线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002:41-52.