考虑风场条件的一类平流层飞艇返回过程建模与航迹规划研究*

孙 帅，李智斌，田科丰

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

平流层飞艇的上升与返回过程是目前飞艇研究领域的一个热点.如何使大型飞艇不依靠其他辅助工具(如降落伞等)，以一种保证外形恒定，保证安全的方式从平流层驶回地面并且精确返场，是目前国内外研究中的一大难题.

在平流层飞艇研究的相关文献中，对飞艇返回过程轨迹规划问题关注较少;而在已有研究上升过程轨迹规划问题的文献中，文献［1］中飞艇建模过程中只考虑了飞艇依靠浮力上升，忽略了气动力的作用;文献［2］中的飞艇模型假令质量随高度变化，在任意位置与飞艇的浮力平衡，但未考虑内外压差变化对飞艇外形的影响.本文根据飞艇气囊内外保持恒定压差的假设，利用浮力、气动力对飞艇进行操纵，建立了一种全新的飞艇三维运动模型.

同时，航迹规划问题是飞艇返回过程制导控制研究的基础.传统的航迹规划问题主要是以直接打靶法代表的直接法和基于Hamilton方程的间接法.而近年来发展起来的高斯伪谱法以其收敛速度快，精度高，逐渐被广泛采用于飞行器航迹规划研究中.

本文基于高斯伪谱法设计了飞艇返回过程时间最短和燃料消耗最优的准则下的参考航迹，同时考虑了大气密度温度状态，以及不同高度风场的变化，有一定的工程参考价值.

1 飞艇模型的建立

1.1 模型总体参数设计

本文中采用文献［2-3］所用的飞艇模型，其中艇长为l=200 m，气囊直径d=500 m，气囊总体积Uh=263 746 m3.

值得说明的是，文献［2］将飞艇的工作高度与压力高度设置为相同值，本文为确保安全，给飞艇高度控制留出一定裕量，在研究中将目标高度设置为21 km，略低于压力高度24 km.

另外，在文献［3］中将最大速度限设定为20 m/s，但其在仿真过程中速度已经超过速度限，并且从经验来看飞艇的速度即使达到35 m/s是完全正常的.故本文在研究中将速度限设定为

30 m/s.

1.2 建立坐标系

首先定义4个坐标系［4］:

1)艇体坐标系:原点取在飞艇质心(航迹研究中考虑压心、质心重合);Ox1轴与艇体纵轴重合，指向头部为正;Oy1轴位于艇体纵向对称平面内，与Ox1轴垂直，指向上为正;Oz1轴垂直于Ox1y1平面，方向按右手法则确定.

2)航迹坐标系:原点位于飞艇质心;Ox2与飞艇速度矢量方向V重合;Oy2轴位于包含速度矢量V的铅垂面内，垂直于Ox2轴，指向上为正;Oz2轴垂直于其他两轴并构成右手系，在航迹系中的速度为V2.

3)速度坐标系:Ox3轴与飞艇质心的速度矢量V重合;Oy3轴位于艇体向对称平面内与Ox3垂直，指向上为正;Oz3垂直于Ox3y3平面，与两轴构成右手系.

4)地面坐标系:原点A选在放飞起点上;Ax轴沿水平面指向目标点，Ay轴沿垂线向上;Az轴与其他两轴垂直并构成右手系.

需说明的一点是，下文中变量角标带数字的即说明该变量定义在对应坐标系内.

定义攻角α，侧滑角β，为速度矢量V在艇体对称平面内与体轴Ox1的夹角和速度矢量与艇体纵向对称平面的夹角.

定义航迹倾角θ，为飞艇速度矢量V与水平面间的夹角.速度矢量在水平面上方为正.航迹偏角为ψV，是速度矢量V在水平面中投影与地面系Ax的夹角.

1.3 大气及风场模型的建立

采用标准大气模型［5］可知0～30 km任意高度大气的温度和气压值，再通过理想气体状态方程，得到大气密度.

风场模型采用文献［3］中北半球某地秋季的风场数据，经过多项式拟合，得到

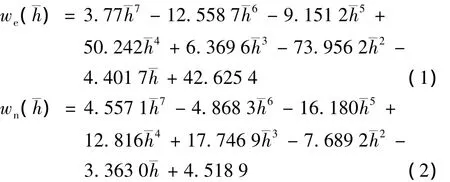
式中，we为风速Vw东向分量，wn为北向分量，利用正态化方法得到标准高度=(h-μd)/σd，正态化参数 μd=12 135，σd=902 2，h为飞艇距海平面垂直高度.

在海拔高度8～16 km东风的风速达到30 m/s以上，已经基本接近于飞艇的最大允许速度，这对飞艇的制导控制造成了很大的不便，所以设计出一条满足各项约束的返回轨迹就显得尤为重要.

1.4 飞艇质心运动动力学模型的建立

方程中各量角标均对应1.2节中坐标系.根据速度的合成与分解，对于航速矢量V，有

考虑到风速也是在地面惯性系下研究，而飞艇的速度则是在航迹坐标系下，所以需将飞艇的速度投影到惯性坐标系中得到

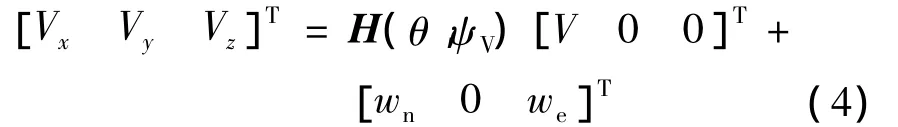
此时认为气流没有垂直方向的运动，H(θ，ψV)为速度系到地面系的坐标转换矩阵，得到

同时，根据牛顿第二定律

式中Ω为航迹坐标系相对地面系的转动角速度，m为飞艇总质量，其中合外力F如下所示:

式中G、B、A3和T2分别为重力，浮力，气动力和推力.因为受力情况在航迹坐标系中研究，所以须将上式中的量投影到航迹坐标系中.

在航迹坐标系下，有Ω×V2=VΩz2j2-VΩy2k2，根据航迹坐标系与地面惯性系的转换关系，有Ω=，其中j2、k2为单位向量

dVw项是在地面惯性系中，可以利用惯性系到航迹坐标系的转换阵将其投影到航迹坐标系，有

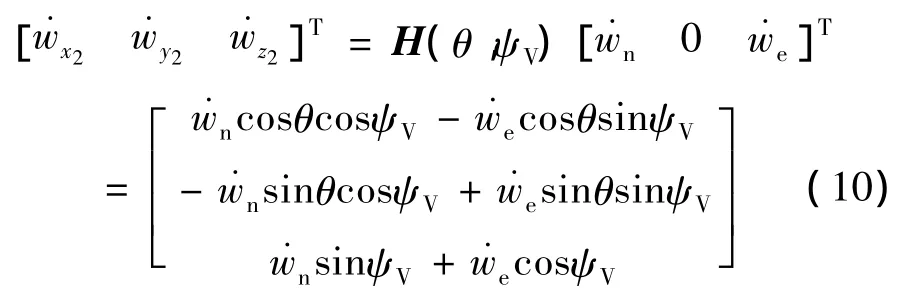
重力G与浮力B均在地面惯性系中，按照坐标系相对关系，有

气动力A3表示在飞艇速度系中，当不考虑速度系与航迹系的夹角速度倾斜角以及气动产生的侧向力时，速度系与航迹坐标系重合，于是有

式中，L为气动升力，D为气动阻力.

同理，螺旋桨推力T表示在航迹坐标系中有

H(α，β)为本体系到速度系的转换矩阵，同时在飞艇研究中，认为飞艇的速度系与航迹坐标系重合，则H(α，β)也为本体系到飞艇航迹坐标系的转换阵.

飞艇在下降过程中为了维持气囊内外恒定压差，则需不断吸入空气.此时飞艇质量会发生很大变化，有压强关系

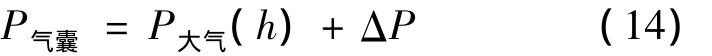
其中内外压差ΔP=300 Pa且飞艇内冲入的氦气质量是一定的，同时认为飞艇内部气囊与外界大气热量交换足够快，气囊内外气体温度一致，应用理想气体状态方程，氦气体积为

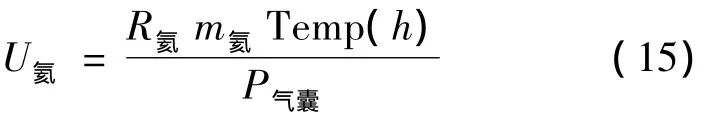
其中Temp(h)为不同高度上的大气温度，R氦为状态常数.

飞艇总体积一定，则空气体积可以得到U空气=Uh-U氦，则可以得到气囊中空气质量

从而可以得到飞艇质量随高度变化的关系式

式中ms为飞艇中气体以外的固定质量.

综合以上结果，可得

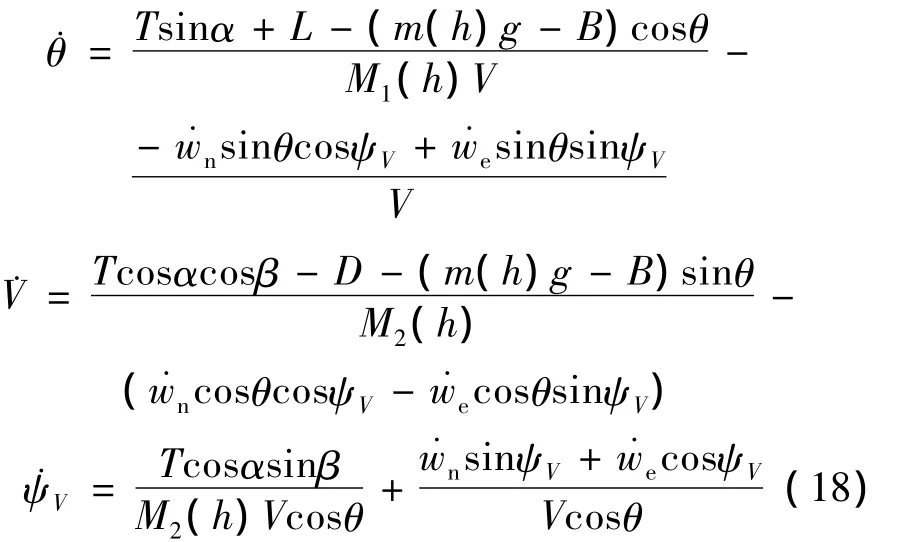
因为飞艇内部充满大量气体，其在大气中运动时产生的附加质量效应不能忽略，在上式中有［2］

2 优化问题的建立与求解

根据以上假设与推导建立了一类飞艇三维运动的动力学模型;根据此模型，将研究飞艇返回过程的航迹规划.轨迹规划问题可看作一个非线性规划问题来求解［2-3，6-7］，其中规划目标为燃料消耗最省或时间最优.其性能指标函数分别为

式中:u=［αTβ］T为飞艇的控制输入，其中α、T和β分别为瞬时平衡［4］的攻角、螺旋桨推力和侧滑角;A为控制量功率消耗加权阵;t0，tf分别为返回过程的初始时刻和末时刻.

考虑动力学的微分约束，利用辛普森公式将微分约束离散化

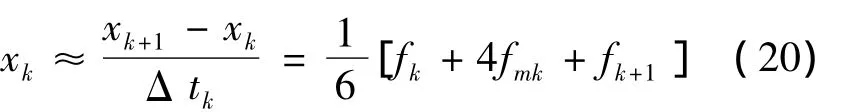
初始状态为

考虑边界约束与末端约束

再利用基于Matlab的GPOPS工具包，进行数值求解.

3 仿真结果分析

对于能耗最优回收模式，对应仿真结果为图1和图2，设定燃料消耗指标为式(19)，其中

因为u中第1，3项攻角和侧滑角的变化可以认为是升降舵和方向舵的舵面操纵，且变化速度较慢，能耗较小;而第二项为飞艇主推螺旋桨，考虑需要耗费较大的电能，所以加权值较大.

可将飞艇回收轨迹按任务时间可分为以下3个模式阶段:

1)水平巡航阶段(0～6 000 s):飞艇在21 km平流层高度，向东飞行45 km，向南飞行16 km.在起始阶段飞艇沿北风顺风飞行约4 km，随即逆风向南飞行.在此阶段飞艇推力，以及攻角、速度均保持在一个恒定值.此阶段主要是为穿越强风带，并且能够到达目标点留出足够多的空间裕量.

图1 能耗最优条件下飞艇状态分析(高度h，航速v，攻角α，推力T)Fig.1 The airship states under the optimal fuel consumption(height h，velocity v，attack angle α，thrust T)

图2 能耗最优条件下飞艇三维航迹Fig.2 The 3-D Trajectory of airship under the optimal fuel consumption

2)快速穿越阶段(6 000～9 000 s):飞艇从21 km到达4 km左右高度，其中快速穿越了8～18 km附近很强的东风带，穿越过程中飞艇顺风朝向东北方飞行，在此过程推力值及攻角不断增大.随攻角由负值变向正值的过程，飞艇下降速度由快到慢.

3)寻的调整阶段(9 000 s～tf):在此过程中，飞艇推力和攻角变化较为剧烈，不断调整航速以及航迹倾角与偏角，达到目标值.

对于时间最优回收过程，仿真结果对应图3和图4.其指标函数为式(19).以任务时间来划分，时间最优飞艇回收过程轨迹可分为两个阶段.

1)巡航调整阶段(0～1 000 s):飞艇在21 km高空逆风巡航飞行，飞艇推力保持在一个比较高的量级(＞5 kN)，使得飞艇一直在最大航速运行.

2)快速下降阶段(1 000～3 700 s):飞艇顺风飞行，并且推力保持在最大值，不断调整攻角，以调整航速，最终达到目标状态.

图3 时间最优条件下飞艇状态(高度h，航速v，攻角α，推力T)Fig.3 The airship states in the timing optimal process(height h，velocity v，attack angle α，thrust T)

图4 时间最优状态飞艇三维航迹Fig.4 The 3-D Trajectory of airship in the fuel consumption optimal process

4 结论

综上所述，在采用浮力与气动力复合控制方法下的定压飞艇的航迹较为类似，均在平流层巡航一段距离，然后以较大的速度顺风穿越激流区.最后到达目标状态.这也给工程实践带来一定启示.特别是燃耗最优的轨迹设计中，在高空阶段飞艇推力值要求较小，这对全电飞艇主推螺旋桨的选取提供方便，能够很好地结合工程实践.

在以后的工作中，可以进一步对压差变化的动态过程进行考虑，另外大气温度的变化也可更加细化的体现在模型中，从而设计出更具有实践参考价值的飞艇航迹.

［1］吴雷，李勇，李智斌.平流层飞艇高度压差协调控制策略［J］.中南大学学报(自然科学)，2011，42(1):327-332.WU L，LI Y，LI Z B.Coordinated control strategy of pressure difference and height of stratospheric airships［J］.Journal of Central South University(Science and Technology)，2011，42(1):327-332.

［2］JOSEPH B M，YIYUAN J Z.Optimal ascent trajectories for stratospheric airships using wind energy［J］.Journal of Guidance Control，and Dynamics，2009，32(4):1232-1244.

［3］SANGJIONG L，HYOCHOONG B.Three-dimensional ascent trajectory optimization for stratospheric airship platforms in the jet stream ［J］.Journal of Guidance，Control，and Dynamics，2007，30(5):1342-1352.

［4］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2012:30-43.

［5］U.S.Standard Atmosphere.National oceanic and atmospheric administration［S］.TR NOAA-ST 76-15672，Washington D.C.，1976.

［6］GUO X，ZHU M，ZHENG Z W，et al.Ascent trajectory optimization for stratospheric airship with thermal effects［R］.Washington D.C.:AIAA，2012:1-19.

［7］李智斌，孙帅，田科丰.考虑热力耦合和质量变化的平流层飞艇运动建模［J］.浮空器研究，2012，6(4):15-17.LI Z B，SUN S，TIAN K F.The study of dynamic coupling with thermodynamics model of high altitude soft airship［J］.The Study of LTA，2012，6(4):15-17.