基于多目标遗传算法的水资源优化配置研究——以徐州市为例

张伟 聂锐 王慧

基于多目标遗传算法的水资源优化配置研究
——以徐州市为例

张伟 聂锐 王慧

本文以可持续发展理论为指导思想，以社会、经济和生态环境多目标协调发展为宗旨，构建水资源优化配置模型，借助Matlab工具箱中的多目标遗传算法进行求解，以期获得社会、经济、生态环境协调发展的最佳综合效益。并以徐州市沛县为例进行算例分析，得出沛县2015年规划水平年的水资源优化配置方案，验证了该方法的可行性和有效性，为徐州市水资源的高效利用提供理论借鉴和实践依据。同时本文的研究还对保护南水北调东线工程的顺利实施，促进整个南水北调沿线地区的社会经济发展也有着重要的意义。

水资源配置 多目标 遗传算法 徐州市

一、引言

近年来，资源短缺、环境恶化、灾害频发等严重阻碍了我国社会经济的发展，特别是我国水资源东多西少、南多北少，空间和时间的分布不均使得水资源利用率及其低下。因此如何合理分配有限的水资源、提高水资源的利用价值便成为亟待解决的问题。本文以区域水资源系统为研究对象，依据可持续发展基本理论和技术、经济、管理等手段，对地表水、地下水、南水北调水和中水四种水源，通过技术手段和管理方式的优化，在各分区内的工业、农业、生活和生态环境四种用水部门间进行科学分配，以规避该地区水资源时间和空间分布的不均衡风险，实现水资源的高效利用和社会、经济、生态环境的协调发展。为了研究的便捷性和直观性，本文以徐州市为例进行水资源配置的算例分析[1]薛丽芳、谭海樵、孔祥光：《基于水安全的徐州城市发展策略》，《成都理工大学学报(自然科学版)》2009年第5期。。

徐州市位于江苏省西北部、苏鲁豫皖四省交界处，是重要的综合性交通枢纽和淮海经济区的中心城市。早在八十年代，徐州市就被列为全国40个严重缺水城市之一。改革开放以来徐州市人口、经济和空间快速增长，与此同时带来了资源匮乏、环境破坏等严重不协调问题，特别是水资源和水环境问题。近年来，水质型缺水更为严重，水资源问题已严重制约了该地区经济社会的持续发展。因此，如何高效利用有限的水资源，提高水资源的利用率，便成为徐州市社会经济发展亟待解决的问题。对徐州市水资源进行优化配置，不仅有利于徐州市水资源的合理开发和高效利用，还对保护南水北调东线工程的顺利实施，促进整个南水北调沿线地区的社会经济发展也有着重要的意义[1]钱学智:《南水北调实施后徐州市水资源利用问题及对策》，〔蚌埠〕《治淮》2009年第5期。。

根据以上研究目标，本文以可持续发展理论为指导思想，构建基于经济、社会、环境协调发展的多目标优化模型，并借助遗传算法进行求解，以获得该地区的最佳综合效益，最后以徐州市沛县为例进行算例分析，验证该方法的可行性和有效性。

二、水资源优化配置的内涵

区域水资源优化配置具有其独特的内涵，其中的“优化”主要是指水资源“质”和“量”在空间和时间上的合理分配及不同用途水源的合理转化；“配置”既包括不同用途水源质和量的转化，也包括水资源时间和空间二维度质和量的分配[2]Jonathan I.Matondo.A comparison between conventional and integrated water resources planning and management. Physics and Chemistry of the Earth,2002，27（11-22）：831-838.。水资源优化配置需从我国国情和水情出发，结合当地的社会、经济和生态环境情况，因地制宜，按当地发展计划，有条件分阶段的实现水资源开发上的优化配置和水资源使用上的优化配置，从而获得社会、经济、生态环境协调发展的最佳综合效益[3]杜守建：《区域水资源优化配置研究——以南水北调东线山东受水区为例》，西安理工大学出版社2006年版，第20-23页。。

1.水资源优化配置的内容

量、质、时、空是自然资源的基本属性。水资源优化配置包括水量、水质、时间和空间这四种基本配置要素[4]李少华、董增川、李玉荣：《水资源统筹配置综述与展望》，〔南京〕《水利经济》2007年第2期。。

（1）水量要素

量是水资源最基本的属性，不同分区、不同用水部门间存在不同的水量要求。因此，需要在系统内进行各分区和用水部门间水资源数量的合理分配。

（2）水质要素

由于各用水部门对水质的要求不同，如果分配给该用水部门的水量不满足水质的要求，水量的供水功能也就降低或消失，因此在进行水量配比的同时还需考虑水质的因素，按照优水优用、促进污水资源化的原则，结合水量进行分质供水。

（3）空间要素

由于水资源的特殊性，其空间分布很不均匀，而且各地区经济、社会和生态发展状况不尽相同，对水资源的需求也不同，因此水资源优化配置在该市的具体实施必然要考虑在空间进行不同层次配置的问题。

（4）时间要素

由于水资源受天然降水的影响比较大，具有很大的不确定性，与用水部门用水的时间和水量存在差异，因此需要通过工程技术措施（拦蓄、储存等）和科学管理手段对水资源进行时间上的配置，使其能够适时适量地满足用水要求[5]杜守建：《区域水资源优化配置研究——以南水北调东线山东受水区为例》，西安理工大学出版社2006年版，第20-23页。。

2.水资源优化配置属性

水资源同时具有自然和社会属性，水资源优化配置是一个多目标（社会、经济、环境）、多水源（地表水、地下水、南水北调水、中水）、多主体（工业用水、农业用水、生活用水、生态用水）的复杂决策系统。

水资源优化配置的实质是实现水资源质和量在时间、空间以及用途上的合理分配，因此它具有多层次、多水源、多主体、多目标的属性。

（1）多水源

以徐州市水资源系统为例，水源包括当地地表水、地下水、南水北调东线调水和中水（污水回收再利用水）。根据徐州市水资源条件、经济发展水平、工程技术水平、社会习俗等因素，在所有水源中优先配置当地地表水资源，其次是地下水、中水，然后是南水北调水。

（2）多要素

水资源具有水量、水质、时间、空间等要素，而水资源的供水、发电、航运等目标正是由这些要素和属性所决定的。水资源具有量质统一性，因为水质不达标而无法满足特定的功能；水量过少或过多都会影响到水能资源的利用；时间、空间分布不均亦会导致不必要的浪费。

（3）多用户

水资源优化配置的实质是通过各种措施和手段将水资源分配到各用水户，因此，掌握各用水户的用水特性、用水需求、用水发展趋势等，对制定用水计划和拟定配置方案都具有重要的作用。本文将用水划分为生活、农业、工业和生态四大类。根据水法规定以及公平、高效为原则，首先满足城乡居民生活用水，并兼顾农业、工业、生态环境以及航运等用水需求。

（4）多目标

水资源的利用具有多目标性，通常分为供水、发电、航运、养殖、生态保护等；从水资源利用效益角度，将其划分为经济目标、社会目标和生态目标，各目标之间往往是矛盾的，而且是不可公度的。传统的水资源优化配置多盲目追求可供水量或经济效益最大化；而可持续发展框架下的水资源优化配置在追求经济效益的同时，还强调了用水公平和环境完整性，是更加复杂的多目标决策问题，宜采取定性与定量相结合的综合集成方法进行。

三、水资源优化配置模型——以徐州市为例

区域水源包括当地水源和外调水源，其中当地水源又分为地表水、地下水、中水，外调水源指南水北调水等。每个水源的特点不同，水价不同，是一个多水源多目标多用户的水资源优化配置与调度问题。本文根据区域水资源现状构建了4水源、3目标、4用户的优化配置模型。

1.区域划分与水源、用户构成

（1）区域划分

徐州市辖5个区（即鼓楼区、云龙区、铜山区、贾汪区、泉山区）、5个县（即丰县、沛县、睢宁县、新沂市、邳州市）。因此本研究按照行政区划将徐州市划分为7个区域，即徐州市区（包括鼓楼区、云龙区、贾汪区、泉山区）、铜山区、丰县、沛县、睢宁县、新沂市、邳州市。

（2）用户级别

在水资源系统中有很多用户，各用户对水资源需求的质和量都不尽相同，因此可根据徐州市的社会经济状况，依据水资源对用户的重要程度，对用户级别进行划分：第一级为生活用水和生态用水，生活用水较其他种类用水更重要；第二级为工业生产用水，工业用水产生的经济价值较其它种类用水高；第三级为农业灌溉用水。当供水不足时，优先供应级别较高的用水户。

（3）水源级别

水资源系统中四种水源的来源不同，其调节能力等也不同，可根据各水源的特性及调剂能力对水源级别进行界定：根据我国水资源实际，供水次序为先地表水，再地下水，后中水，对于南水北调东线水源，根据调水的成本和实际情况，调水成本较高，故最后考虑。当供水发生时，优先考虑级别高的水源。

2.目标函数

水资源优化配置的目的是实现水资源合理配置以实现整个区域资源、社会、经济、环境的可持续发展。一般讲，水资源优化配置的目标应包含经济效益目标、社会目标和生态目标三个方面。由于这三个方面的目标不同，且具有不可公度性，因而考虑采用多目标优化模型，各目标函数分别为：经济目标、社会目标和生态目标。

（1）经济目标：用水产生的经济效益扣除总成本之后的净效益最大

式中：Skij为水源i向k子区j用户的供水量（m3）；akij为水源i向k子区j用户的单位供水量效益系数（元/m3）；ckij为水源i向k子区j用户的单位供水量成本系数（元/m3）。

（2）社会目标：缺水量之和最小

式中：Dkj为k子区j用户的需水量（m3）。

（3）生态目标：生态用水量得到最大满足

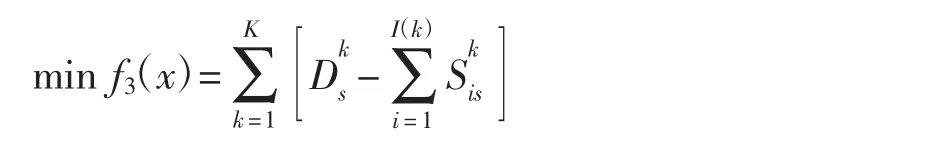
式中：Dks为k子区生态需水量（m3）。

3.约束条件

在进行优化计算的过程中除了要考虑上述三个目标外，还要考虑多方面的约束条件，其中较为重要的为水量约束，包括供水约束与需水约束。供水约束要求某一水源向不同地区不同用水户供应的水量之和不超过其可供给量，需水量约束本着节约的原则，要求不同水源向某一用水户供应的水量之和不超过其需求量[1]E.Kondili，J.K.Kaldellis.Model development for the optimalwater systems planning.Computer Aided Chemical Engineering，2006，21（2）：1851-1856.。

（1）水源可供水量约束

不同水源的特性不同，其供水量约束条件也不同，各水源分别为：地下水、地表水、中水和南水北调水。

①地表水可供水量约束：由于地表水可供给量取决于该地区水利工程规模

和管理方式，不同地区地表水资源可供给量不尽相同。计算时段中，某一地表水源地调出的地表水量之和不超过该地区的地表水可供给量。表示为：

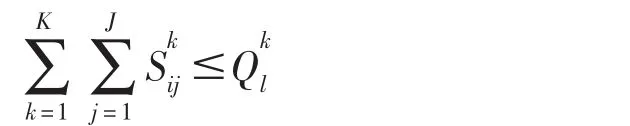
式中：Skij为l地表水供给k子区j用户的水量（m3）；Qkl为k子区l地表水的总供水量（m3）。

②南水北调东线调水量约束：根据南水北调东线的来水情况及供水能力，各分区所用南水北调东线调水总量不能超过该时段供水干渠分水口的可供水量。

式中：Skj为南水北调东线供给k分区j用户的水量（m3）；Wk为k分区南水北调东线的总供水量（m3）。

③地下水、中水可供水量约束：地下水、中水的可供水量约束大体一致，以地下水为例：不同子区不同用户所用地下水总量不能超过各水平年可供的地下水可供水量。

式中：Skj为浅层地下水供给k子区j用户的水量（m3）；Gk为k子区浅层地下水的总供水量（m3）。

（2）需水量约束

需水量约束是指不同水源地向某一用水户供水的总量之和不能超过该用户的需水量。由于工业、农业、生活和生态环境用水户的特点不同，其需水量约束条件也不同。特别是对于生活需水来说，涉及到人的基本生存安全，在进行优化分配前要首先满足保证生活最低需水量。

这里以工业需水量约束为例来说明：不同分区各水源供给某一工业用水户的水量之和不应超过该水平年工业用水户的需水量。

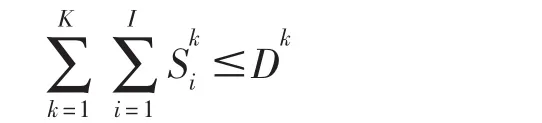
式中：Ski为k子区i水源供给一般工业的水量（m3）；Dk为k子区一般工业总需水量（m3）。

（3）水库蓄水约束

要保证水库的蓄水量在其正常范围内，限制水库的蓄水量范围如下：

Vmin≤Vt≤Vmax

式中：Vt为水库蓄水量（104m3）；Vmin、Vmax分别为水库的最小、最大蓄水量（104m3），最小蓄水量为水库死库容，最大蓄水量当汛期时为汛限水位下蓄水量，非汛期为正常蓄水位下蓄水量。

（4）非负约束

四、模型的求解

1.方法的选择

对于建立的多目标水资源优化配置模型，很难用某种优化方法寻求最优解，因此对于复杂系统的优化问题，我们更多的关注解的不断改进。

遗传算法是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应搜索算法。由于其具有健壮性，特别适合于处理传统搜索算法解决不了的复杂的和非线性问题[1]Goldberg D E.Genetic algorithms in search optimization and machine learning.Reading,MA:Addison_Wesley,1989.。同时，Math－Works公司的矩阵计算软件MATLAB提供了遗传算法与直接搜索工具箱(Genetic Algorithm and Direct Search Toolbox)，用户可以根据需要通过工具箱调用遗传算法函数，大大加大了该方法实用性和便捷性。因此，本论文考虑用遗传算法对该多目标问题进行求解。

MATLAB 7.0中的遗传算法工具箱提供了一个比较友好的界面，用户只需输入必要的参数便可用遗传算法对模型进行优化。

2.参数的确定

（1）单位供水量效益系数（akij）

根据徐州市2010年工业总产值（3114.09亿元）、工业需水总量（32208.6万m3）、农业总产值（514.73亿元）、农业需水总量（342808.2万m3），可测算出工业、农业供水量效益系数为9668.505元/ m3、137.954元/m3。由于生活用水和生态环境用水所产生的效益多为社会效益，目前很难定量化，在本研究中为了体现首先保证生活用水，其次生态用水，再其次其它类型用水的配水原则，我们赋予生活供水量效益系数为20000元/m3，生态环境供水量效益系数为15000元/m3[1]陈南祥、李跃鹏、徐晨光：《基于多目标遗传算法的水资源优化配置》，〔北京〕《水利学报》2006年第3期。。

（2）单位供水成本系数（ckij）

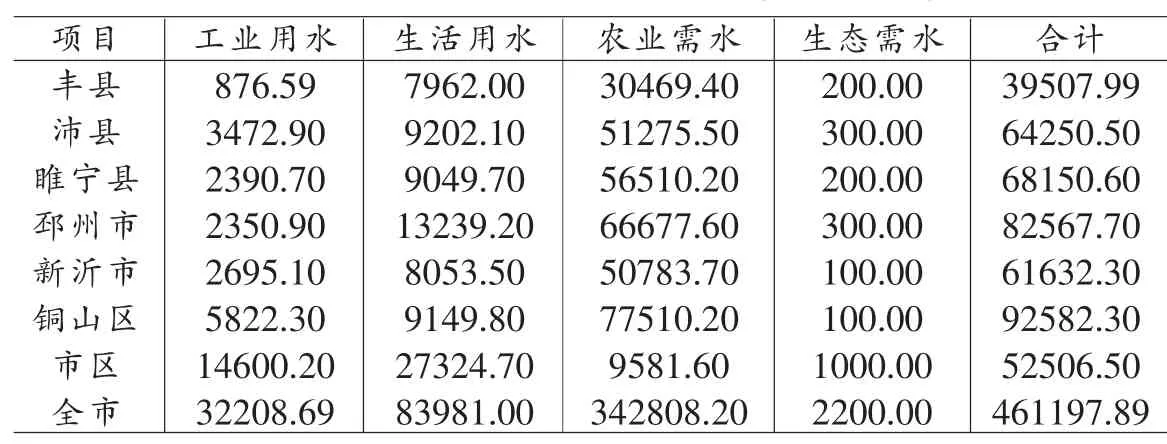
表1 徐州市各行政区域需水量（单位：万m3）

表2 徐州市多年平均水资源总量汇总表（单位：万m3）

表3 2015年徐州市沛县水资源优化配置结果表（单位：万m3）

在本模型中该系数可由水源i向j用户的供水价格来表示，根据徐州市供水价格调查结果及统计资料显示：①地下水、地表水：根据对该市现状自来水厂资料分析，目前该市自来水综合供水价格在3.1元左右，工业用水价格为3.57元/m3，生活用水价格为2.72元/m3。由于徐州境内多为地表引流，本研究假定地表水、地下水价格均为自来水价格。②中水：徐州某开发区新水源再生水厂经过污水处理后的中水成本大约为2.0-2.5元/ m3，向工业用户的出售价格为3.4元/m3，该价格低于目前该市工业用自来水水价3.57元/m3。由此看来，不管是从经济效益来讲还是从节约资源来讲，中水利用都是应该大力提倡的。③南水北调水：在核算调水工程成本的基础上，秦长海（2010）认为资本金利润率为8%的前提下徐州市南水北调东线水价为3.80元/m3[2]高斌：《区域水资源优化配置及供水系统规划研究》，天津大学出版社2009年版，第37-45页。。

（3）各分区不同用户需水量

根据徐州市十二五发展规划，王超（2009）预测2015年徐州市各分区不同用户需水量见表1所示：

（4）各分区不同水源可供水量

根据徐州市十二五发展规划，各分区不同水源可供水量如下表2所示。

3.求解过程——以沛县为例

由于调研过程中数据资料的缺失及时间限制，在此仅以沛县为例用遗传算法进行优化配置算例分析，其它子区域及全市的水资源优化配置方法与此类似。

借助MATLAB的遗传算法工具箱，系统计算得出18种配置方案，我们选取其中6组进行分析（见表3），水量对比结果见表4，各分配方案的目标函数值见表5所示。

表4 优化前后水量对比结果表

表5 各分配方案的目标函数值表（单位：万元）

由表3、4可以看出，优化的地下水、地表水、中水和南水北调水可利用量在6个分配方案中均未超过该地区可利用量。从表5和图3可以看出为决策者选出的6组方案中第二、六方案侧重经济目标，第四方案经济效益最差；第四方案侧重社会目标，其次为第一、三方案，第二方案社会目标最差；第四方案生态目标最为显著，第三、五方案次之，第二方案生态目标最差。结合表5中的数据，决策者可以根据自己的需要做出选择。

五、结论

本文以可持续发展理论为指导思想，构建基于经济、社会、生态环境协调发展的多目标水资源优化模型，借助Matlab工具箱中的多目标遗传算法求得Pareto最优解，并以徐州市沛县为例进行算例分析，得出沛县2015年规划水平年的水资源优化配置方案，为徐州市水资源的高效利用提供理论借鉴和实践依据，以期获得经济、社会、生态环境协调发展的最佳综合效益。由于数据资料收集和时间的限制，本论文的研究仅限于初步，进一步的研究需在以下几个方面进行完善：（1）对优化模型的目标函数和约束条件进一步完善，解决水质型缺水问题；（2）扩大研究区域范围，对整个徐州市（6区6县）的水资源进行系统配置；（3）完善多目标不确定性问题的求解方法，尝试其它方法（如进化算法、PSO粒子算法等）以选择更为合适的。

〔责任编辑：天则〕

Research on Optimal Allocation ofW ater Resources Based on M ulti-Objective Genetic Algorithm—a Case Study of Xuzhou

Zhang Wei Nie Rui Wang Hui

According to sustainable development theory,the present paper constructs a multi-objective optimalmodel of water resource allocation based on the coordinated development of economy,society and ecological environment,which is solved by genetic algorithm of Matlab,expecting comprehensive developmental benefits of economy,society and ecological environment in Xuzhou.Then Peixian of Xu Zhou is app lied to a calculation analysis of samp les,concluding an optimal allocation scheme of water resource in 2015,which verifies feasibility and effectiveness of thismethod,both theoretically and practically supporting highly efficient utility of water resources in Xuzhou.At the same time,this research can promote the imp lementation of South-to-North Water Diversion Project.

water resource allocation;multi-objective;genetic algorithm;Xuzhou

张伟，中国矿业大学管理学院博士研究生 221009

聂锐，中国矿业大学管理学院教授 221009

王慧，中国矿业大学管理学院讲师 221009

教育部人文社会科学研究青年基金项目（11YJC630205），水资源配置中的期权契约设计及其最优策略研究——以南水北调东线为例；中国矿业大学社会科学基金（2009W4），水资源配置中的期权契约设计及其最优策略研究——以南水北调东线为例；中国矿业大学211工程三期重点学科建设项目（A90202），煤炭产业发展战略与煤矿安全管理。