基于相似模型的导管架平台波浪载荷数值模拟

刘 伟，刘金梅

（东北石油大学 机械科学与工程学院，黑龙江 大庆163318）①

海洋平台作为海上油气生产的基地，必须对其安全性进行准确的评估。对于离岸结构，波浪载荷是平台设计的主要载荷，作用在水深100 m平台上的风压力与波浪压力的合力超过1×105k N［1］。结构最主要的交变应力是由于波浪的不规则变化形成的［2］。模拟技术是处理随机海浪与建筑物相互作用的重要手段［3］。在一定的海洋环境载荷作用下，利用有限元软件分析能够快速而又准确地计算分析出桩腿桩靴各个时刻的受力变形情况，得到结构各点的应力历时曲线［4］。本文以导管架平台为研究对象，应用有限元法，根据5阶Stokes波浪理论［5］，对波浪耦合作用下海洋平台的静动力响应进行数值模拟研究，分析结构在波浪作用下的变形及受力状态，为现场工程应用和安全诊断提供参考。

1 模型建立及参数确定

1.1 导管架平台数值建模

试验平台以某导管架海洋平台为原型，按照相似比1∶50研制而成。模型为8桩腿9层结构，平台高4.980 m、长1.735 m、宽1.390 m；甲板长1.689 m、宽1.270 m 。如图1。

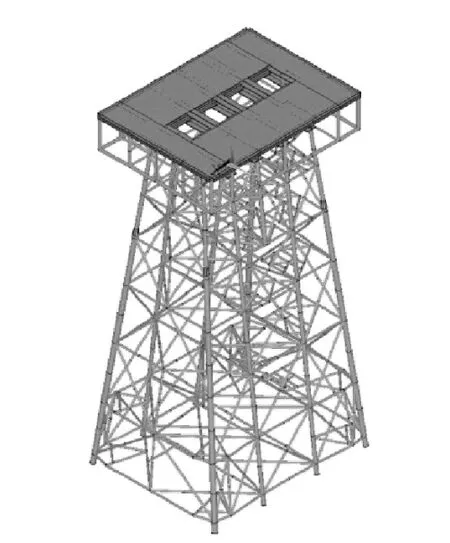
图1 平台数值分析模型

按照有限元分析理论，建立该平台的数值分析模型。平台的各离散单元主要是空间管单元、梁单元以及壳单元，分别模拟结构的导管、甲板横梁以及甲板，模型共有608个节点，964个单元。

1.2 波浪模型比尺及计算参数

在惯性力和重力起重要作用的流动中，欲使2个几何相似的物体满足动力相似条件，必须保证模型和实物的弗劳德数相等［6］，即

由式（1）进行推理变换，可以得到采用正态模型进行模拟试验时的各物理量比尺，如表1。

表1 波浪模型物理量比尺

按照表1中的比尺和实际海洋环境确定计算参数，如表2。

表2 波浪载荷计算参数

2 结果分析

2.1 模态分析

用有限元分析软件中提供的Block Lanzcos法计算提取模型的低阶频率及振型。此法采用Lanzcos算法，将对称矩阵通过正交相似变换变成对称三对角矩阵，并自动采用稀疏矩阵方程求解器，适用于计算某系统特征值谱所包含的一定范围内的固有频率。

通过计算得到前3阶频率分别为22.835、25.423、37.400 Hz。在前3阶频率下的振型如图 2所示。1阶振型表现为y方向弯曲；2阶振型表现为x方向的弯曲；3阶振型表现为xy方向的扭曲。

图2 平台前3阶振型

2.2 波流耦合作用下的静力分析

根据模态分析所得到的前2阶固有频率，可计算得到导管架平台瑞利阻尼系数为：α＝3.024 67，β＝1.318 71×10－4。

2.2.1 相位角搜索

在采用5阶Stokes波浪理论时，相位角的取值对作用于结构的波流载荷值影响明显。在进行结构静力分析时，假定波浪以最大作用力的方式作用于结构物，以此来考虑结构受力的最不利工况。因此，在进行静力分析之前，对相位角从0～360°进行搜索，以找到波流耦合力最大时的相位角取值，以此结果作为静力分析时的输入条件［7］。

根据分析结果数据得到波流耦合力－相位角关系曲线，如图3所示。相位角为224°时，波流偶合力最大，最大值为258.076 N。

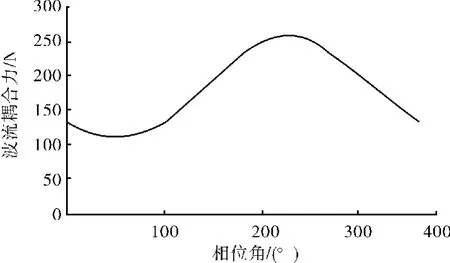
图3 波流耦合力－相位角关系曲线

2.2.2 波浪静力分析

在有限元分析软件中，将相位角搜索结果通过WATERTABLE定义到波浪载荷，通过SOLUTION项进行求解，即可在后处理器中观察结果。分别得到导管架平台的变形云图（如图4）、单元应力云图（如图5）。

图4 平台变形云图

图5 平台单元应力云图

由图4可以看出：结构发生最大位移的位置位于平台顶部，数值为5.29×10－5m。由图5可以看出：结构的最大应力为3.6 MPa，发生在桩腿底部位置。

2.3 波浪载荷下平台结构瞬态动力分析

计算采用5阶Stokes波浪理论，波浪载荷沿x轴方向0°入射，作用于平台，分析所取的作用时间为50 s，时间间隔0.2 s。

分析得到平台甲板中心节点在波浪载荷作用下x、y方向的位移时程曲线，如图6所示。由图6可知，y方向的位移响应明显小于x方向的响应，且在0°附近。因此，后面的分析主要考虑x方向的响应。

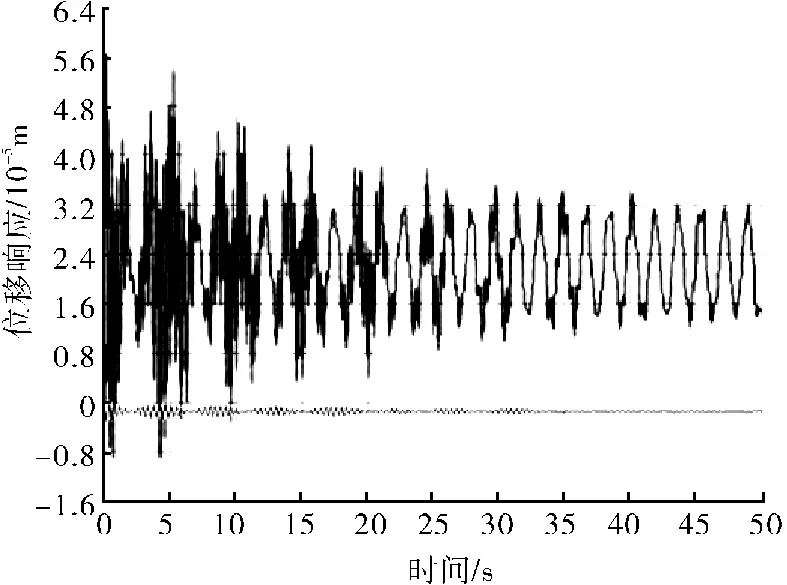
图6 平台甲板中心节点x、y方向位移时程曲线

对平台甲板中心、主导管水面、中部以及泥线处4个节点的位移响应进行分析，得到平台不同位置x方向位移时程曲线，如图7所示。由图7可知：平台不同位置的位移响应不同，从泥线往上，响应值依次增大；平台在波浪作用下，平台从初始位置发生偏移，结构在载荷作用初期的振动没有规律性，一段时间之后，趋于稳定，保持在某一平衡位置作类似周期往复振动，周期约等于波浪周期。

图7 平台不同位置x方向位移时程曲线

对结构弱点应力进行分析，得到应力时程曲线，如图8所示。由图8可知：应力变化也呈现出一定的周期性，在初期应力值较大，平台的运动稳定后，应力值始终维持在约2 MPa。

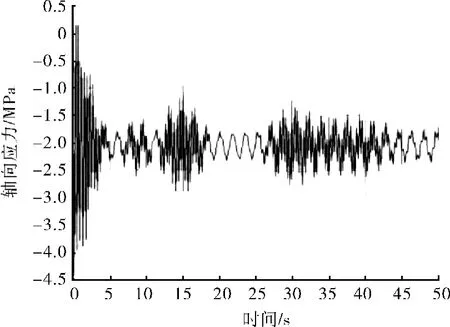
图8 结构弱点应力时程曲线

3 结论

1） 应用5阶Stokes波浪理论描述波浪运动，模拟海洋平台的波浪载荷，可以得到比较满意的结果。

2） 采用数值模拟的方法可以较精确地模拟海洋平台在波浪载荷作用下的静动力响应，确定结构的薄弱部位，为现场安全作业提供参考。

3） 以导管架平台为例进行数值建模和仿真分析，得到平台在波浪载荷作用下产生类周期往复运动，周期与波浪周期基本一致；平台不同位置的响应值不同，从泥线至平台顶端，响应值逐渐增大，平台甲板结构变形明显，最大应力出现在桩腿底部位置。

［1］ 方华灿.海洋石油工程［M］.北京：石油工业出版社，2010.

［2］ 张淑华，徐磊，钱进.海洋导管架平台疲劳问题分析［J］.石油矿场机械，2012，41（11）：16－19.

［3］ 张金平，段艳丽，刘学虎.海洋平台波浪载荷计算方法的分析和建议［J］.石油矿场机械，2006，35（3）：10－14.

［4］ 谢娜娜，马廷霞，刘国昊，等.自升式海洋平台桩腿桩靴有限元分析［J］.石油矿场机械，2013，42（11）：32－38.

［5］ 文圣常，宇宙文.波浪理论与计算原理［M］.北京：科学出版社，1984.

［6］ 孟祥玮，高学平，孙精石.波浪模型试验中水密度对相似性的影响［J］.水道港口，2007，6（28）：391－396.

［7］ 杨进，刘书杰，姜伟，等.ANSYS在海洋石油工程中的应用［M］.北京：石油工业出版社，2010.