设计规范中统一无缝线路稳定性计算公式存在的问题分析
徐玉坡,梁 晨,卢耀荣
(中国铁道科学研究院铁道建筑研究所,北京 100081)
《铁路无缝线路设计规范》(以下简称《规范》)[1]附录B中规定无缝线路稳定性控制采用修改后的“统一无缝线路稳定性计算公式”进行计算,其中变形波长计算式作了实质性修改。“统一无缝线路稳定性计算公式”及其计算参数曾不止一次进行修改,而每次修改后似乎又有新的问题。本文首先简介《规范》中经过修改的统一无缝线路稳定性计算公式,再对公式存在的问题从理论分析和实际计算两方面加以论证。
1 公式简介
《规范》中的无缝线路稳定性计算公式形式如下

式中:Pw为温度力,N;β为轨道框架刚度系数;E为钢轨弹性模量,MPa;Iy为一股钢轨的截面对垂直中和轴线的惯性矩,cm4;f为轨道弯曲变形矢度,采用0.2 cm;foe为轨道原始弹性弯曲矢度,cm;l为轨道弯曲变形半波长,l=l0,l0为轨道原始弯曲半波长,cm;《规范》定义foe/l2为轨道原始弹性弯曲相对曲率;Q为等效道床横向阻力,N/cm;R为曲线半径,cm;1/Rop为轨道塑性原始弯曲曲率,1/cm;《规范》中定义t为轨道原始弹性弯曲相对曲率,t=foe/l20,1/cm。
2 存在问题
无缝线路设计稳定性允许温升的计算,首先应用式(2)计算温度压力作用下无缝线路的弯曲变形波长l,再将计算的l代入式(1)计算温度力Pw,从而计算得允许温升[ΔTu]。式(1)与原“统一无缝线路稳定性计算公式”形式相同,参数取值有所不同,而式(2)是作了实质性修改的变形波长计算公式。
式(2)分子第二项只能>0,则
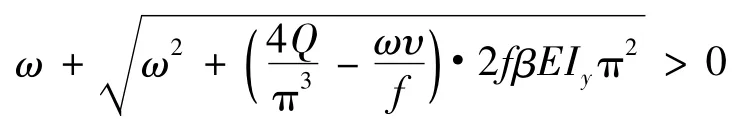
当式(2)分母趋近于0时,计算得l趋近于∞;当式(2)分母<0,则l2<0,可得l为虚数。
显然无缝线路弯曲变形波长的计算结果为∞或为虚数是不合理的。当然还应进一步研究导致这种计算结果的条件及原因,下面就从理论和实际计算两个层面分析存在的条件。
2.1 理论分析
结构平衡稳定理论将失稳现象分为两类:第一类失稳现象以理想中心受压直杆为典型;第二类失稳现象以埋置在弹性介质中具有初始弯曲的长梁为典型,隔水板、输油管道和无缝线路的失稳属于此类。第二类失稳特征是梁一开始就处于同时受压和受弯,随着轴压力增大,梁弯曲变形逐渐增大,即弯曲变形矢度增大、波长增大。当梁弯曲变形处于临界状态,即使轴压力微量增加,或有外力干扰,弯曲变形都会增大而至梁失稳。第二类失稳过程通过结构平衡状态曲线P-f,l-f的计算可描绘出。
从式(1)、式(2)来看,无论 ω,t,Q 的大小,亦即无论线路曲线半径、轨道结构刚度、原始弯曲和道床横向阻力的大小,当无缝线路承受温度压力由小逐渐增大时,相应弯曲变形矢度f也由小逐渐增大,总存在,使l为虚数;当弯曲变形矢度f增大至某一量值时趋近于0,则l为∞;弯曲变形矢度f继续增大,弯曲变形波长l才为实数。从理论层面分析,用式(1)和式(2)计算无缝线路弯曲变形的过程,弯曲变形波长的变化总存在一个无法确定的过程,因此也就无法计算得到P-f,l-f平衡状态曲线和失稳特征,与结构平衡稳定理论相悖。
2.2 实际计算
通过实际计算验证式(2)分母≤0的可能性。首先要求采用计算参数符合实际,则参数取值要以试验为依据,并得到一些专家在文献资料中公开认可。若用式(1)和式(2)进行计算,在钢轨类型和曲线半径一定的情况下,对轨道框架刚度系数β、道床横向阻力Q、原始弯曲相对曲率等的取值分析如下。
1)轨道框架刚度系数β。在《规范》中规定有砟轨道的β为1.0。有砟轨道框架对弯曲变形的阻抗,只考虑2根钢轨的刚度,不计扣件阻矩的作用,这与国内外实测轨道框架的刚度有差异。在广钟岩等编著的《铁路无缝线路》(1995年,第1版)中将混凝土轨枕线路β定为1.5,范俊杰编著的《现代铁路轨道》(2001年,第2版)中将道岔直线轨道框架刚度系数β定为2.0。本文用于公式验算,取β为1.5。
2)等效道床横向阻力Q。在《规范》中规定,Ⅱ型轨枕等效道床横向阻力Q=85 N/cm。道床横向阻力不仅与轨枕类型有关,也与道床状态有关。养护维修作业后道床松散,横向阻力显著降低。参见卢耀荣著《无缝线路研究与应用》[2]、广钟岩等编著的《铁路无缝线路》[3],道床清筛作业后,实测的道床横向阻力Q=45~60 N/cm。文献[3]中用于设计时,Ⅱ型轨枕Q=79.2 N/cm。文献[4]的算例中Q=75 N/cm。本文取Q=80 N/cm。
3)原始弯曲相对曲率。《规范》规定了原始弯曲相对曲率,将其按塑性和弹性进行分解,其中塑性占83%,明显与铁路现状不符。铁道部2013年及2006年颁布的线路维修规章对原始塑性弯曲作了严格限制。通常原始弹性弯曲总大于原始塑性弯曲,若将原始弹性弯曲定为占总量的83%反倒接近实际。即使用于设计,文献[3]中,弹性原始弯曲也占总原始弯曲的50.00% ~58.33%。
下面用经过分析接近实际的参数、具有代表性的轨道,对修改后的公式作计算验证。
1)算例1
CHN60型钢轨、Ⅱ型混凝土枕Q=80 N/cm、β=1.5,初始弯曲相对曲率 f0/l2=2.103 ×10-6cm-1,其中弹性 f0e/l2占 83% 为1.745 49 ×10-6cm-1,塑性f0p/l2占17%,为3.575 1 ×10-7cm-1,f=0.2 cm。代入上述参数后,计算结果如下:
2)算例2
用于设计,偏于安全考虑,原始弯曲相对曲率分解为弹性 f0e/l2占58.33%,为1.226 7 ×10-6cm-1,塑性f0p/l2占 41.67%,为8.763 2 × 10-7cm-1。仍 用CHN60型钢轨,Q=80 N/cm,β=1.5,f=0.2 cm。计算结果如下:
由以上算例结果可知,当采用接近实际的参数时,用式(2)计算无缝线路弯曲变形波长l,存在l为∞或为虚数的情况。即使用于设计将原始塑性弯曲相对曲率偏于保守取值,l为∞或为虚数的可能性仍然存在。
3 结论及讨论
对《铁路无缝线路设计规范》中“统一无缝线路稳定性计算公式”存在的问题进行分析后,提出以下几点看法:
1)理论分析证明,随着无缝线路弯曲变形矢度f由小到逐渐增大,一定范围内必存在弯曲变形波长l为虚数或∞的情况,l存在不确定性,进而P-f,l-f函数关系不确定,也就无法描述失稳特征和过程及求取临界温度力、临界变形矢度和临界变形波长,有悖结构平衡稳定理论。
2)用接近实际的计算参数、具有代表性的轨道,对修改后的公式作计算验证,证明计算的弯曲变形波长l为∞或为虚数并非偶然,有一定的必然性和普遍性。即使设计时参数取值偏于保守,一定的线路平面条件下,计算的l也同样存在为∞或虚数的情况。用修改后的“统一无缝线路稳定性计算公式”,似难完成铺设无缝线路允许温差表的计算。
3)用修改后的公式计算弯曲变形波长l也并非任何计算条件下得出的结果均为∞或虚数。若原始塑性弯曲所占百分比取得很大,就不存在这种情况,但相应的计算条件是实际铁路不允许存在的,参数取值欠缺充分依据。
4)本文讨论尚未涉及重载铁路铺设特重型钢轨、Ⅲ型弹条扣件的无缝线路。若用修改后的公式计算重载铁路无缝线路的弯曲变形量,因ω,β值比本文用于计算验证的值还要大,或经破底清筛的道床变得松散使得Q值显著降低,则l为 ∞或虚数的可能性大为增加。
5)国外列入设计规范的无缝线路稳定性计算公式有很多,如:德国拉波公式、英国萨姆维达公式、俄罗斯别尔申公式、美国考尔公式、日本沼田实公式、匈牙利霍姆公式等。国内许实儒、胡津亚、广钟岩等都曾提出过计算公式。铁科院也提出不等波长稳定性计算公式。尽管各种公式存在不完善之处,但尚未发现计算的无缝线路弯曲变形波长为∞或虚数的情况。作为纳入《规范》中的计算公式理应严谨,建议编制单位对修改后的“统一无缝线路稳定性计算公式”存在问题深入研究,予以纠正。
[1]中华人民共和国铁道部.TB 10015—2012 铁路无缝线路设计规范[S].北京:中国铁道出版社,2012.
[2]卢耀荣.无缝线路研究与应用[M].2版.北京:中国铁道出版社,2010.
[3]广钟岩,高慧安.铁路无缝线路[M].4版.北京:中国铁道出版社,2010.
[4]许实儒,童本浩.铁路轨道基本理论[M].北京:中国铁道出版社,1997.

