无背索独塔斜拉桥静力力学性能试验研究

程 功，伍建强

(1.云南第二公路桥梁工程有限公司，云南昆明 650205;2.江西省交通科学研究院，江西 南昌 330038)

1 工程概况

某大桥主桥为跨径209.601 m(主跨，钢箱梁段)+(50+40)m(副孔，预应力混凝土变截面箱梁段)的无背索独塔斜拉桥。斜拉索共两个索面，横向索间距为0.9 m，均布置在中央分隔带处;顺桥向索距为13 m，呈竖琴形布置。索塔竖直高度111.89 m，在距桥面约30 m处分成两肢，呈人字形。桥面横向布置:0.25 m栏杆+2.0 m人行道+3.0 m非机动车道+0.25 m隔离带+7.50 m机动车道+2.0 m拉索区+7.5 m机动车道+0.25 m隔离带+3.0 m非机动车道+2.0 m人行道+0.25 m栏杆，桥面总宽28.0 m，在主塔处变宽至34 m。主桥下部构造:主塔处采用圆形实体直嵌式基础，辅助墩采用薄壁墩、桩基础。设计荷载等级为公路—Ⅰ级(校核荷载为城—A级)，设计安全等级为一级。大桥立面及试验控制断面布置见图1。

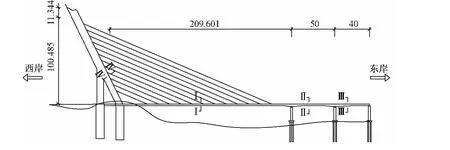
图1 大桥立面及试验控制断面布置(单位:m)

2 试验内容及方法

2.1 试验计算

全桥运营阶段的内力及加载效率按平面杆系模型计算分析［1］，采用有限位移理论(考虑结构非线性)进行斜拉桥初始平衡状态分析，计算中考虑施工过程和实际桥梁的成桥内力状态［2-3］，梁、塔单元截面采用实际截面，索单元采用Enrst公式以考虑其垂度效应，斜拉索在塔、梁锚固的偏心用刚臂单元模拟，求出合理的成桥状态后进行加载计算。各试验工况的理论值采用空间模型计算分析，分析的基础为前一步得出的成桥状态。空间模型采用索单元、梁单元及薄板单元分别模拟斜拉桥的斜拉索、主塔及主梁。平面杆系计算模型如图2所示，空间计算模型如图3所示。

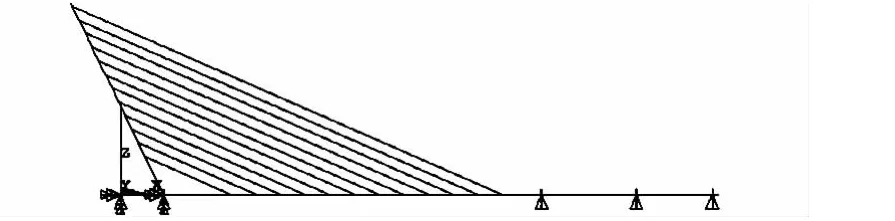
图2 平面计算模型

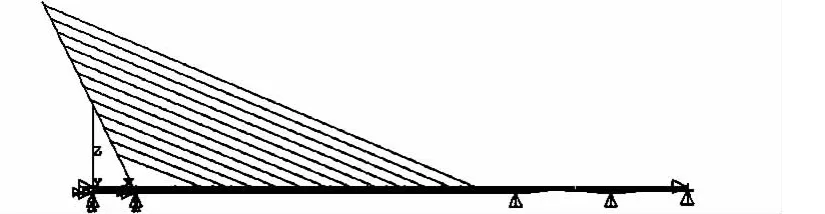
图3 空间计算模型

2.2 试验加载工况及测试内容

试验采用18辆三轴自卸载重车作为加载车辆，各辆重车均在33 t左右。因尚未正式通车，试验前使用部分加载车在桥上缓行几次并停放，进行预压，以消除结构塑性变形，并调试测试系统以进入正常的工作状态。本次试验分8种测试工况:①主跨(钢箱梁段)主梁正弯矩最大;②斜拉索索力最大;③50 m跨主梁正弯矩最大;④40 m跨主梁正弯矩最大;⑤主孔与50 m跨之间墩顶主梁负弯矩最大;⑥50 m与40 m跨之间墩顶主梁负弯矩最大;⑦索塔弯矩最大;⑧塔顶位移最大。

试验时采用偏载与对称两种加载方式，以研究结构偏载和对称加载工作性能。在影响线分析的基础上，为缩短现场试验工作时间，将试验工况①、②合并处理，将工况⑦、⑧合并处理。各试验工况均采用4～5排(共18辆)重车进行加载，通过适当调整车辆纵距，使试验荷载达到加载效率。试验加载分级进行，分级数不少于3级，通过控制加载车数量进行加载分级。

2.3 测点布置

1)主梁应力测点布置

主桥钢箱梁L/2控制截面(Ⅰ-Ⅰ截面)顶板布置6个应变花测点(T1～T6)，U形肋布置10个纵向应变测点(L1～L10);底板外部布置2个应变花测点(B2，B5)、4 个纵向应变测点(B1，B3，B4，B6)，测点布置如图4。

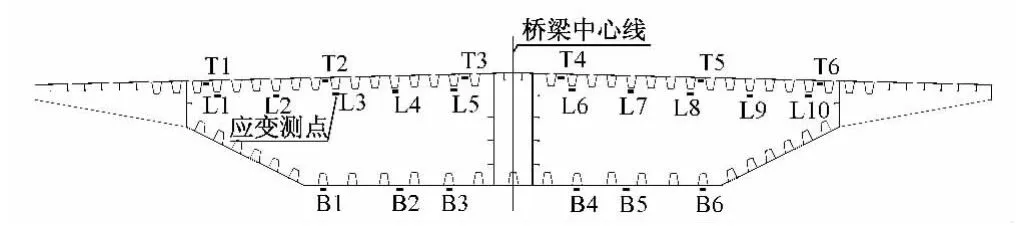
图4 主跨钢箱梁L/2控制截面应变测点布置

50 m跨最大正弯控制截面(0.4L控制截面Ⅱ-Ⅱ)及40 m跨最大正弯控制截面(0.3L控制截面Ⅲ-Ⅲ)梁底布置5个纵向应变测点，如图5所示。主跨与50 m跨之间墩顶及50 m与40 m跨之间墩顶主梁最大负弯矩控制截面梁底布置5个纵向应变测点。

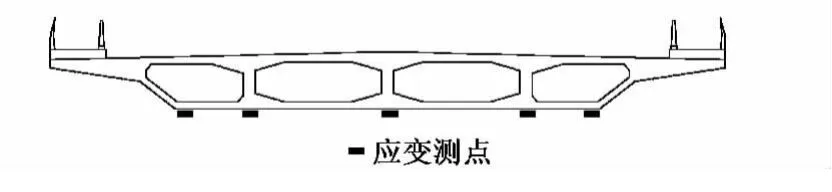
图5 40 m及50 m跨控制截面应变测点布置

2)斜拉索索力测点布置

对全桥拉索在恒载下的索力进行测试，并在工况②下对S5，S6，S7号索进行测试(吊索编号由东岸至西岸依次编号)。

3)主梁挠度及桥面挠度测点布置

在主跨L/2控制截面、50 m跨0.4L控制截面及40 m跨0.3L控制截面处桥面上、中、下游横桥向布置3个挠度测点。在桥面各吊索位置处上下游侧分别布置挠度测点，如图6。

图6 主跨桥面挠度测点布置

4)塔顶位移测点布置

在主塔顶预先设置光学棱镜，用精密全站仪监测塔顶位移。

5)主塔根部截面应力测点布置

在主塔根部截面(Ⅳ-Ⅳ截面)布置2个应变测点，测试主塔控制截面混凝土应变。

3 主要试验成果分析

试验结果表明，各工况下主梁应力校验系数在0.63～0.78，主梁挠度校验系数在0.73～0.97，均满足《大跨径混凝土桥梁的试验方法》中的要求，说明主梁的抗弯强度及刚度均满足设计要求。卸载后弹性恢复非常好，说明主梁、主塔仍处于弹性工作状态。试验应力校验系数η偏低的原因较多，如箱梁剪滞效应的影响、计算模型引起的误差等［4］。偏载试验下，根据实测挠度计算主跨偏载系数为1.12～1.24，略偏大。偏载加载时最大试验荷载下部分试验结果与理论结果的对比如表1所示。工况②测试结果如表2所示，工况⑧测试结果如表3所示。

表1(工况⑦)、表3中试验荷载下实测主塔根部截面应力及主塔塔顶位移均未超过理论值，且应力测试值的绝对值并不大，表明主塔的强度、刚度均达到设计预期。

由表2可见，实测拉索应力增量校验系数在0.94～0.97，与理论计算值较为吻合，表明拉索工作与设计预期一致，拉索工作正常。

工况①主跨L/2测试断面应力变化规律见图7。可见:由于受剪力滞效应及箱梁顶面横坡等因素的影响，顶、底板横向应变分布略有变化。受局部加载的影响，顶板U形肋下缘弯曲正应力在横桥向的分布变化稍大，这主要是因为直接受车轮荷载作用的顶板U形肋下缘应力变化较大。

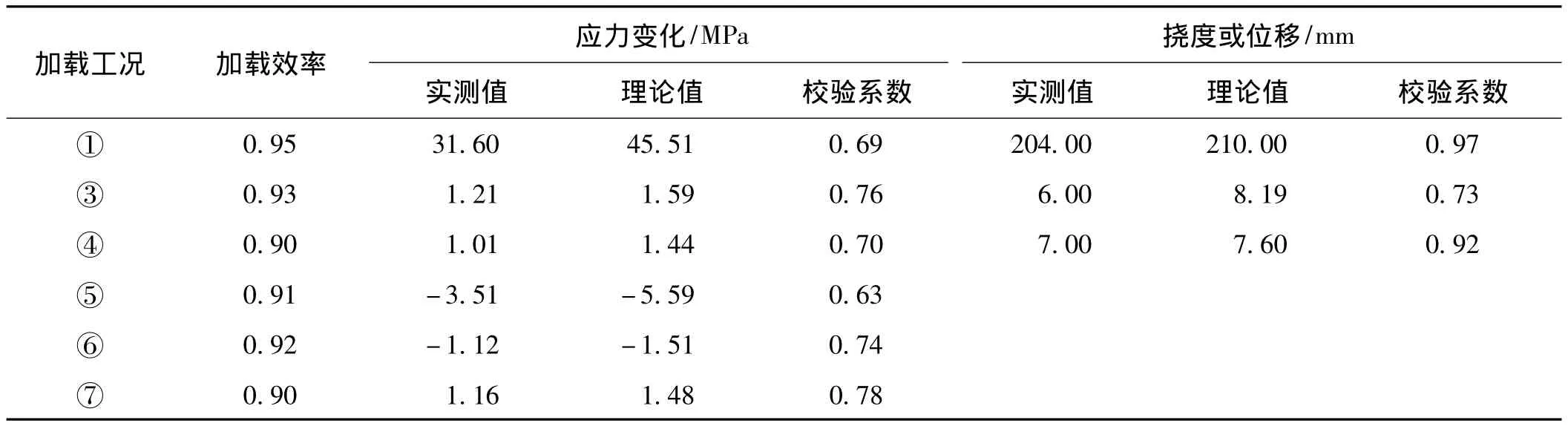
表1 偏载加载时最大试验荷载下部分试验结果与理论结果对比

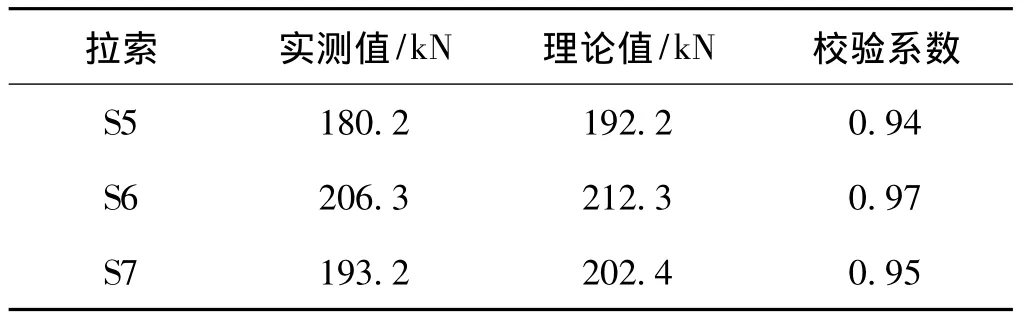
表2 工况②下部分实测索力增量

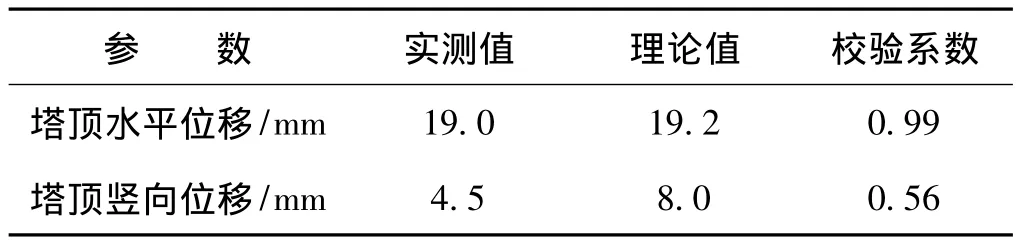
表3 工况⑧下实测位移

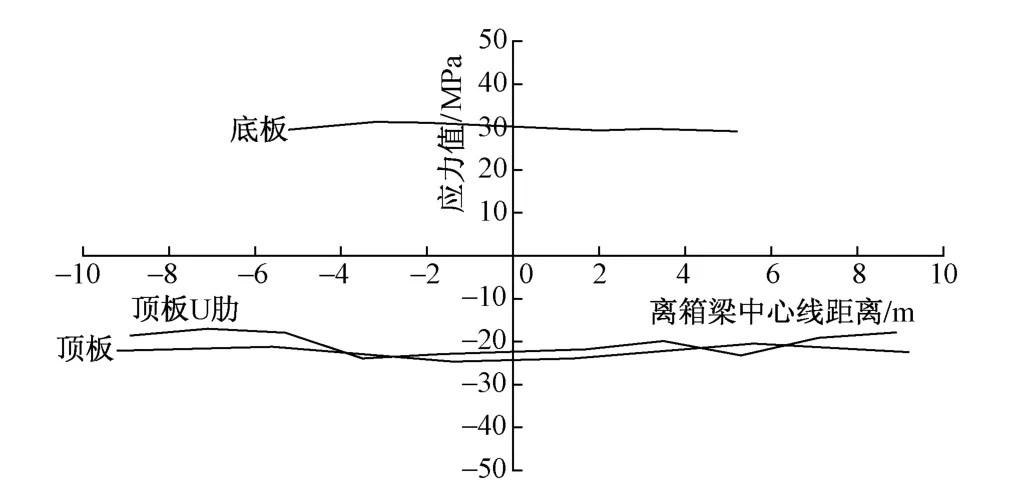
图7 工况1主跨L/2测试断面应力变化规律

工况①主梁变形规律见图8。可知:实测主跨桥梁竖向挠度曲线平顺、光滑，实测值与理论值非常吻合，说明理论计算模型与实桥状态非常接近。实际桥梁索、塔、梁间工作协调与理论预期一致。

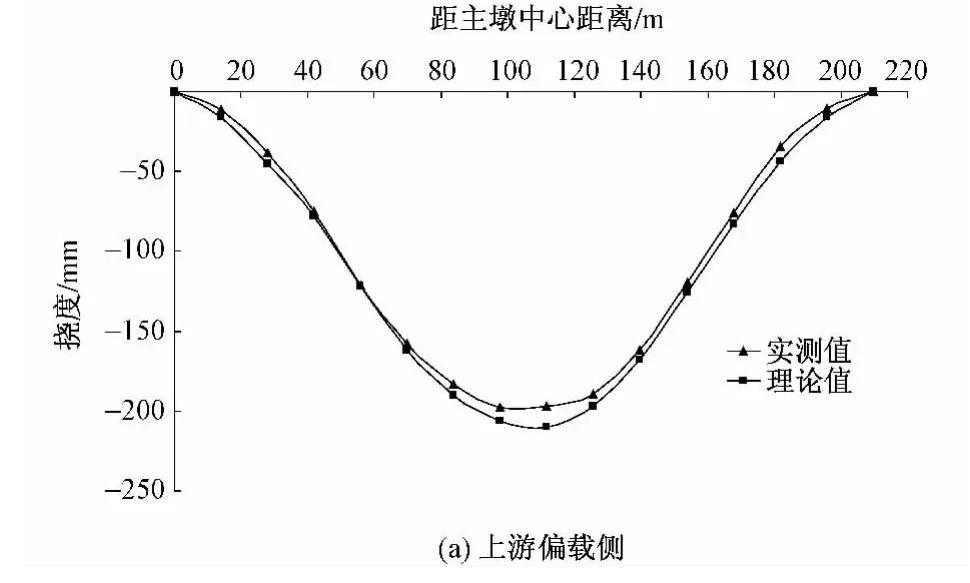
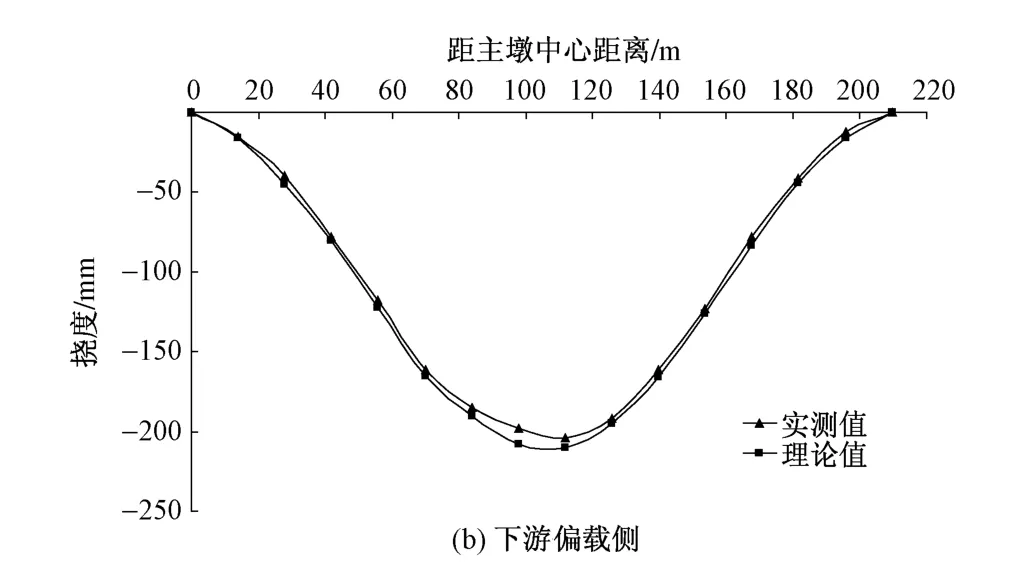
图8 工况①主梁变形规律

4 结论与建议

1)静力试验表明，该桥具有足够的强度、刚度和较好的偏载受力性能，实际结构受力性能与理论计算大致吻合，各试验工况未发现结构工作异常，该桥满足设计荷载标准承载能力要求。

2)主跨L/2测试断面应力横向变化规律表明:钢箱梁顶、底板横向应变受剪力滞效应等因素的影响。因直接受车轮局部荷载的作用，顶板U形肋下缘弯曲正应力在横桥向的分布变化稍大。

3)从桥梁静力受力的情况看，由于没有背索，主塔在使用阶段活载作用下产生较大的朝主跨方向的水平位移，主塔受力不平衡，建议类似桥型推广设计时增设几根背索，以“稀疏背索独塔斜拉桥”作为设计探索方向，以使主塔受力平衡。

［1］交通部公路科学研究所，交通部公路局技术处，交通部公路规划设计院.大跨径混凝土桥梁的试验方法［Z］.北京:交通部公路科学研究所，1982.

［2］林元培.斜拉桥［M］.北京:人民交通出版社，1994.

［3］华孝良，徐光辉.桥梁结构非线性分析［M］.北京:人民交通出版社，1997.

［4］胡强，刘建磊，袁磊.高赞大桥静动载试验研究［J］.铁道建筑，2008(12):18-21.