曲线连续刚构梁桥预应力钢束的简化计算方法

梁新玲，祝 兵，窦胜谭，刘桂满，王俊坪

(西南交通大学土木工程学院，四川成都 610031)

随着我国桥梁工程的蓬勃发展，为获得流畅的桥梁线形修建了大量的曲线梁桥。曲线梁桥能很好地适应地形、地物的限制，而且其结构线条平顺、流畅、明快，给人美的享受。预应力曲线梁桥已广泛地应用于现代公路交通中，在理论研究和工程技术方面已具备了较高的水平。但在高速铁路上应用仍然存在诸多需要完善和改进的地方，预应力的损失就是其中较为典型和突出的问题。

现今很多设计单位在对曲线连续刚构梁桥进行预应力设计时，考虑直接采用直梁代替弯梁进行简化计算。如若设计中对预应力损失估计过低，会导致桥梁在实际运营过程中发生主梁跨中挠度过大、局部开裂等多种问题;如若对预应力损失估计过高，则实际中混凝土必须承受过高的持续压应力，甚至产生过大的反拱度，对结构安全和使用不利［1］。因此，在设计中正确估算预应力损失至关重要［2-4］。

1 工程背景

兰渝铁路黄河特大桥为(80+2×120+80)m曲线连续刚构梁桥。主梁采用单箱单室变截面。箱梁中支点处梁高8.8 m，底板厚120 cm;跨中及边跨现浇段梁高4.6 m，底板厚45 cm，箱梁高度以及底板厚度均按2次抛物线y=0.001 647x2变化。箱梁腹板的厚度按线性变化，中支点处腹板厚100 cm，跨中及边墩支点附近腹板厚50 cm。全桥箱梁顶板厚40 cm，顶宽11.2 m，底宽6.7 m，单侧悬臂长2.45 m，悬臂端厚25 cm，悬臂根部厚65 cm。顶板设90 cm×30 cm的倒角，底板设30 cm×30 cm的倒角。箱梁在刚构墩顶设置了2道厚2 m的横隔墙，在边墩顶设置的横隔墙厚1.4 m。

全桥主梁采用C55混凝土，桥梁下部结构采用双薄壁组合结构，刚构墩墩身采用C40混凝土，墩顶实体段采用C55混凝土。基础采用钻孔灌注桩基础。箱梁采用全预应力理论设计，其预应力施工采用后张法。

2 预应力损失的理论计算

根据设计规范，对于后张法预应力混凝土构件，应考虑以下因素引起的预应力损失:预应力筋与管道壁间摩擦引起的预应力损失(σl1);锚具变形、钢筋回缩和接缝压缩引起的预应力损失(σl2);混凝土弹性压缩引起的预应力损失(σl4);钢筋松弛引起的预应力损失(σl5);混凝土收缩和徐变引起的预应力损失(σl6)。由相关文献［2-3］可得以上5种预应力损失的理论计算公式。

3 模型计算

3.1 模型描述

本文采用有限元软件MIDAS/Civil进行结构的计算分析，计算参数按设计参数取值。

兰渝铁路黄河特大桥的主梁为单箱单室截面的窄长梁，建模时采用单梁截面建立直梁模型与弯梁模型。直梁模型与弯梁模型的预应力钢束布置相同。本文只考虑桥梁的纵向预应力，直梁与弯梁纵向都布设了7组预应力钢束，分别为边跨顶板合龙束N1、边跨底板合龙束N2、边跨顶板束N3、中跨底板合龙束N4、腹板静定束N5，T构静定束N6、中跨顶板合龙束N7。全桥共布置了408根预应力钢筋。均采用φs15.2 mm低松弛钢绞线。其中顶板束沿箱梁顶板布置在边跨端部、边跨合龙段及中跨合龙段;腹板下弯束全部布置在腹板上;底板后期束沿底板线形布置在边跨合龙段及中跨合龙段。T构静定束布置在T构梁段的顶板内，长束布置在上层，短束布置在下层，最上层距顶板0.17 m［5-6］。

3.2 预应力损失获取方法

有限元软件MIDAS/Civil对直梁与弯梁模型进行计算时，各个施工阶段中，对管道摩阻、锚具变形、弹性收缩、预应力筋松弛、混凝土收缩徐变引起的预应力损失都可以提取。本文采用如下方法计算直梁与弯梁的各项预应力损失。

在施工阶段控制选项中关闭收缩徐变和弹性回缩，在钢束特性中关闭松弛和钢束回缩，只保留摩擦系数0.25，偏差系数0.006 6，计算获得管道摩阻损失。锚具变形损失与摩擦有关，所以不关闭摩擦系数，打开钢束回缩，设置为两端各0.006 m，如此获得锚具变形损失。打开施工阶段控制选项中的弹性压缩，计算得到弹性压缩损失。关闭弹性回缩，打开松弛选项，增加时间依存材料，得到松弛损失。关闭松弛，打开施工阶段控制选项中的收缩徐变，用默认的设置处理，计算获得收缩徐变损失。最后打开所有预应力损失，计算得到直梁与弯梁的总预应力损失与有效预应力。

4 计算结果及对比分析

4.1 钢束的各项预应力损失对比分析

按以上预应力损失获取方法对直梁与弯梁的有限元模型进行计算分析，可分别得到直梁与弯梁各组预应力钢束的各项预应力损失。本文以预应力钢束N1，N2，N3，N4，N5，N6 为例，对比直梁与弯梁的各项预应力损失获得两种建模方法在预应力损失上的差值。表1分别给出了各组钢束上直梁与弯梁各项预应力损失的最大差值。

表1 直梁与弯梁各项预应力损失的最大差值 MPa

由表1可知，不同钢束中，弯梁的管道摩阻损失皆大于直梁，其中在预应力钢束N4中直梁与弯梁的管道摩阻损失相差最大，为12.62 MPa，这种差别是由于弯梁预应力钢束的平弯引起的。不同钢束中，直梁与弯梁管道摩阻损失的数值差变化不大，可见钢束的位置对管道摩阻损失的数值差影响较小;钢束的位置对锚具变形损失、松弛损失的数值差影响也不大。直梁与弯梁的锚具变形损失主要集中在两侧锚具处，越远离张拉端，其值越小，这主要是由于反向摩擦力的影响［4］。而且在各组预应力钢束中，除了在钢束 N1，N2，N4的部分区域内，弯梁的锚具损失稍大于直梁，其余钢束中，二者的锚具损失相差很小。直梁与弯梁的松弛损失从钢束的两侧逐渐向中间减小，同时在所有预应力钢束中，直梁的松弛损失都大于弯梁，但是所差甚小。直梁与弯梁的弹性压缩损失受钢束的位置影响较大，在预应力钢束N1，N2中，直梁的弹性压缩损失明显大于弯梁，而在钢束N4，N5，N6中二者的差距很小，甚至在钢束N3的部分区域内，弯梁的弹性压缩损失反而明显大于直梁。由此可见，直梁与弯梁各个部分的弹性收缩变形情况不同，总体上弯梁的弹性收缩变形要弱于直梁;钢束的位置对直梁与弯梁收缩徐变损失的数值差也有较大影响。除了钢束N1，N3的部分区域，弯梁的收缩徐变损失稍大于直梁，其他钢束中，直梁的收缩徐变损失皆大于弯梁。

表1给出的直梁与弯梁预应力损失的最大差值不能避免局部的干扰，无法全面反映出各组钢束中直梁与弯梁各项预应力损失的变化趋势，也无法得出二者所有位置的对比情况。以钢束N2为例，计算出直梁与弯梁各项预应力损失的对比图，发现直梁与弯梁在预应力钢束N2上各项预应力损失的变化趋势与对比情况，能较好地反映出二者各项预应力损失的最终对比结果。在各组钢束中，直梁与弯梁的各项预应力损失的变化趋势是一致的。也可以看出，直梁与弯梁的管道摩阻损失、锚具变形损失、松弛损失都相差很小;弹性压缩损失(图1)与收缩徐变损失(图2)相差较大，而且总体上直梁的损失值要大于弯梁。

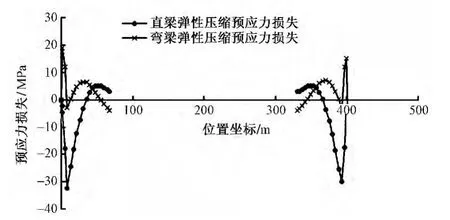
图1 钢束N2的弹性压缩损失对比

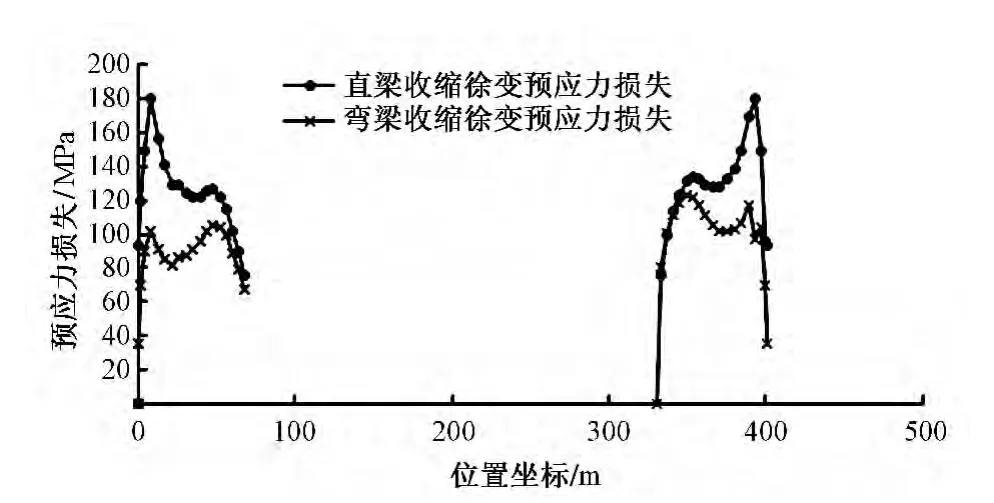
图2 钢束N2的收缩徐变损失对比

4.2 各钢束的有效预应力对比分析

MIDAS/Civil软件考虑所有预应力损失，直接输出直梁与弯梁各组预应力钢束的有效预应力。直梁与弯梁在各预应力钢束上的有效预应力变化趋势是一致的。而且结合表1中直梁与弯梁总预应力损失的比较可得:直梁与弯梁在各预应力钢束上的有效预应力都相差不大。其中在钢束N1的中间部分以及钢束N3的两端(图3)，弯梁的有效预应力略小于直梁，局部最大差值为54.39 MPa，是张拉控制应力的3.40%;在其他预应力钢束中弯梁的有效预应力皆大于直梁，预应力钢束N2在8.25 m和393.25 m处达到最大差值，为47.40 MPa，是张拉控制应力的3.40%。由此可见，直梁的有效预应力稍小于弯梁。

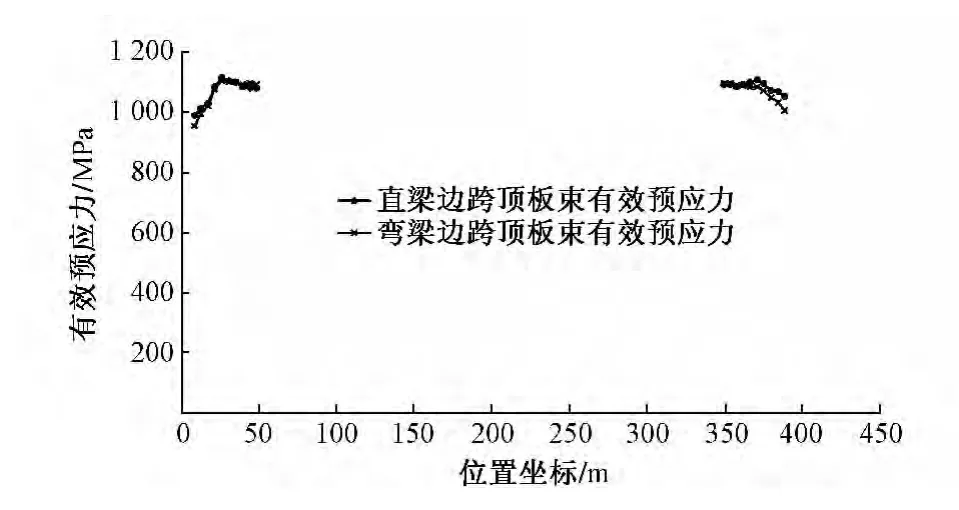
图3 钢束N3的有效预应力对比

5 结论

本文在相同条件下对比直梁与弯梁的预应力损失情况，论证用直梁代替弯梁进行预应力损失简算的可行性。通过对直梁与弯梁各预应力钢束上各项预应力损失，以及总预应力损失与有效预应力的对比分析，得出以下结论:

1)直梁与弯梁各项预应力损失的变化规律相同，而且数值差异不大。其中各钢束的管道摩阻损失，由于弯梁钢束平弯的影响，其值大于直梁，最大相差12.62 MPa，占张拉控制应力的0.92%。此外，直梁与弯梁各钢束的锚具损失与松弛损失都不受钢束平弯的影响，只在局部存在微小差别。各钢束的弹性压缩损失和收缩徐变损失，直梁的值大于弯梁，在底板合龙束中，直梁与弯梁的收缩徐变损失局部相差最大为77.36 MPa，为张拉控制应力的5.55%。所以该桥用直梁代替弯梁进行预应力损失的简算是可行的。

2)直梁与弯梁中不同位置的钢束对二者各项预应力损失的差异影响不同。其中钢束的位置对直梁与弯梁收缩徐变损失与弹性压缩损失的数值差影响较大，而对管道摩阻损失、锚具变形损失以及松弛损失的数值差影响较小。

3)直梁与弯梁的有效预应力变化规律一致。在边跨顶板束和边跨顶板合龙束局部位置，弯梁的有效预应力略小于直梁，其他预应力钢束上弯梁的有效预应力皆大于直梁，由此可见该800 m曲率半径的连续刚构桥采用直梁代替弯梁进行预应力设计是可靠的。

［1］王心顺.非对称高墩大跨曲线连续刚构桥地震反应分析［J］.铁道标准设计，2008(6):55-57.

［2］朱鹏志.连续刚构桥预应力钢束合理布束问题的研究［D］.长沙:长沙理工大学，2007.

［3］郭荣武.连续刚构桥的预应力钢束设计研究［J］.海岸工程，2011(2):22-29.

［4］王阳.大跨度连续刚构桥预应力钢束设计研究［D］.成都:西南交通大学，2011.

［5］朱鹏志.连续刚构桥预应力钢筋合理布束问题的研究［D］.长沙:长沙理工大学，2007.

［6］雷俊卿，王楠.预应力混凝土连续刚构桥施工监测与仿真分析［J］.铁道学报，2006(2):74-78.