Existence and Uniqueness of Strong Solution for Shear Thickening Fluids of Second Grade

BOUSBIH Hafedh and MAJDOUB Mohamed

Universit´e de Sousse,Institut Sup´erieur des Sciences Appliqu´ees et de Technologie de Sousse,Cit´e Ibn Khaldoun,Sousse 4003,Tunisie.

Universit´e de Tunis El Manar,Facult´e des Sciences de Tunis,LR03ES04´Equations aux d´eriv´ees partielles et applications,2092 Tunis,Tunisie.

Existence and Uniqueness of Strong Solution for Shear Thickening Fluids of Second Grade

BOUSBIH Hafedh and MAJDOUB Mohamed∗

Universit´e de Sousse,Institut Sup´erieur des Sciences Appliqu´ees et de Technologie de Sousse,Cit´e Ibn Khaldoun,Sousse 4003,Tunisie.

Universit´e de Tunis El Manar,Facult´e des Sciences de Tunis,LR03ES04´Equations aux d´eriv´ees partielles et applications,2092 Tunis,Tunisie.

Received 25 September 2012;Accepted 24 December 2013

.In this paper we study the equations governing the unsteady motion of an incompressible homogeneous generalized second grade fluid subject to periodic boundary conditions.We establish the existence of global-in-time strong solutions for shear thickening flows in the two and three dimensional case.We also prove uniqueness of such solution without any smallness condition on the initial data or restriction on the material moduli.

Non-Newtonian fluids;generalized second grade fluids;shear rate dependent viscosity;existence;uniqueness;strong solution.

1 Introduction

The theory and the applications of non-Newtonian fluids have attracted the attention of many scientists for a long time since they are more appropriate than Newtonian fluids in many areas of engineering sciences such as geophysics,glaciology,colloid mechanics, polymer mechanics,blood and food rheology,etc.Fluids with shear dependentviscosity, which can exhibit shear thinning and shear thickening and include the power-law fluids as a special case,constitute a large class of non-Newtonian fluids.For instance,see[1–3] for more detailed discussions.

There are many models of non-Newtonian fluids which have recently become to be of great interest.Among these models one can cite fluids of differential type.The secondgrade fluids,which are a subclass of them,have been successfully investigated in various kinds of flows of materials such as oils,greases,blood,polymers,suspensions,and liquid crystals.In the classical incompressible fluids of second grade,it is customary to assume that the Cauchy stress tensor T is related to the velocity gradient∇u and its symmetric part Du through the relation

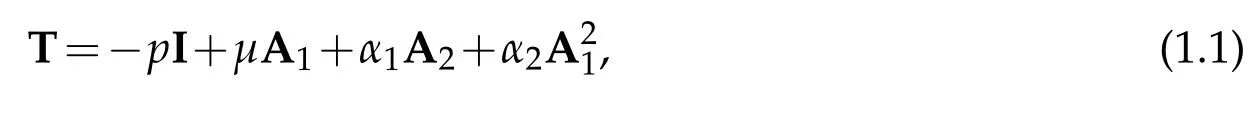
where p is the indeterminate part of the stress due to the constraint of incompressibility, µis the kinematic viscosity,and α1and α2are material moduli which are usually referred to as the normal stress coefficients.The kinematical tensor A1and A2are the first and the second Rivlin-Ericksen tensor,respectively,and they are defined through

where u=(u1,…,ud)and∇u:=(∂jui)1≤i,j≤d(d=2 or 3 is the space dimension)denote the velocity vector field and its gradient.Here∂juistands for the partial space derivative of uiwith respect to xj,i,j=1,…,d.The material derivative is given by

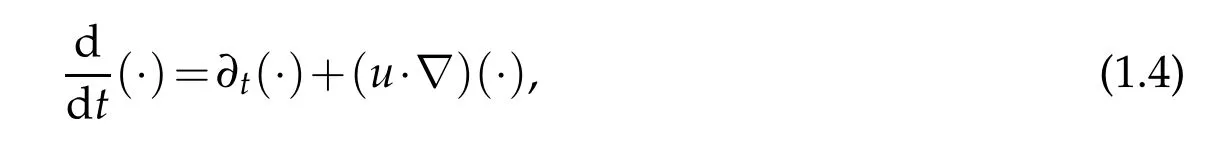
where∂tis the partial derivative with respect to time and(u·∇)the differential operator with respect to the spatial variable defined by

Indeed,in[4],Dunn studied the thermodynamics and stability of second-gradefluids with viscosityµdepending on the shear rate|Du|(i.ep.the Euclidean norm of the symmetric part of the velocity gradient defined byand showed that if the fluid is to be compatible with thermodynamics in the sense that all motions of the fluid meet the Clausius-Duhem inequality and the assumptionthat the specific Helmholtz free energy of the fluid be minimum in equilibrium,thenµ,α1and α2in(1.1)must verify

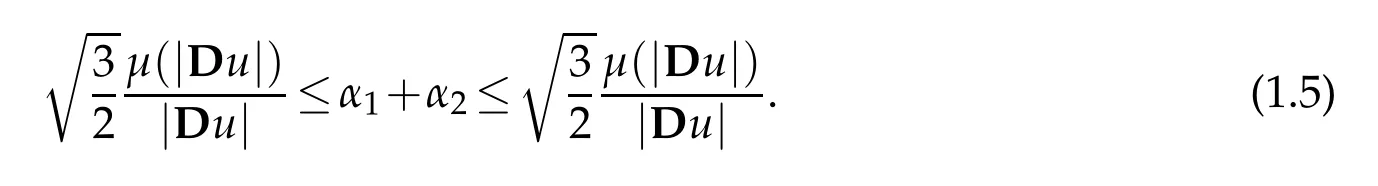
In the 1980s,Man,Kjartanson and coworkers[5]and[6]showed that polycrystalline ice in creeping flow under pressuremetertests can be modeled as an incompressible secondgrade fluid with the viscosity dependingonthe shearrate.The constitutive equationproposed by Man and coworkers,which leads to well-posed initial-boundary-value problems in nonsteady channel flow[7]and can also model the flow of ice in triaxial creep tests[8],is

whereµ(|Du|)=ν|Du|m,with-1＜m＜∞and ν is a material constant.

Man and Massoudi[9]conducted thermodynamic studies on some classes of generalized second-grade fluids,which include the class defined by(1.6).For the case m＞1 of this class,they showed that the viscosity functionµand the normal-stress coefficients must verify the inequality

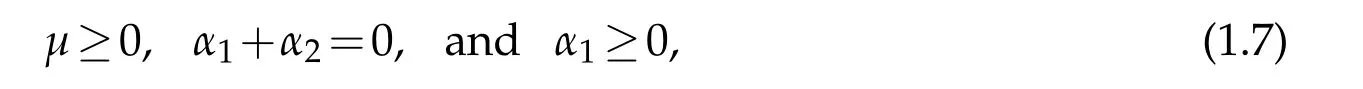
asrestrictionsimposedbythermodynamicsandtheassumptionthatthespecificHelmholtz free energy of the fluid be minimum in equilibrium.

In this paper we study a class of generalized second-grade fluids with constitutive equation given by(1.6),which has its normal-stress coefficients satisfy the equation α1+ α2=0 and has a viscosity functionµ(|Du|)different than that proposed by Man and coworkers.The mathematical assumptions on the viscosity function that we adopt will be given in Section 3.For the class of generalized second-grade fluid in question,the thermodynamic restrictions(1.7)1and(1.7)3are valid[4].

The interested reader can find more about the literature of the generalized fluids of second grade and their applications,for example in[9–11].Henceforth we will adopt (1.7)2and(1.7)3as assumptions.Based on these assumptions and the relations(1.2)-(1.3), one can deduce that the stress tensor(1.6)for generalized fluids of second grade could be written in the following form

Let us mention that by“generalized second grade fluid”we mean a fluid of second grade of type(1.6)(i.e.whose viscosity is a non linear function of the shear rate)as it will be considered in this study,and by word“classical second grade fluid”a second grade fluid (1.1)(i.e.whose viscosity is constant).

Thisworkisdevotedtothemathematical analysis oftheequationsgoverningtheflow of a homogeneous incompressible fluid which occupies all space Rd(d=2;3),the Cauchy stress of which is given by formula(1.8),and the velocity of which is 2π-periodic.We will also assume that the kinematic viscosityµ(|Du|)is a nonlinear function of|Du|. The stress tensor 2µ(|Du|)Du will be denoted by S(Du).Next,we derive the equations modeling our studied system.

Let T be an arbitrary positive real number.We set[0,T]as the time interval and Ω:= (0,2π)dthe periodic box of dimension d.Since the fluid body is taken as incompressible and homogeneous in material,the density of the fluid can be put equal to 1.Then the momentum equation is expressed as

with the condition of incompressibility

Therefore,with the help of relation(1.4),inserting the expression(1.8)and expanding, Eq.(1.9)becomes

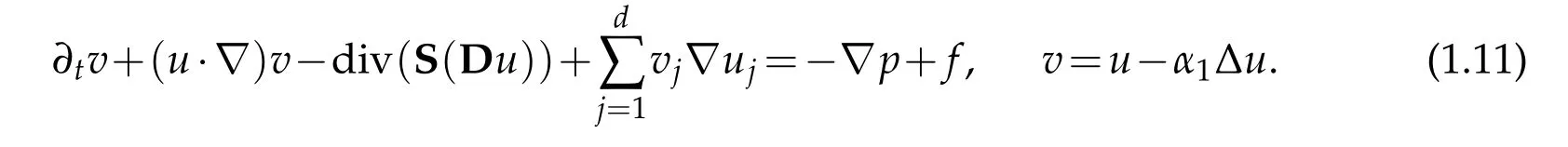
One can look at[12]and more precisely at[13]to verify that the computations in(1.11), holds true.See also[14]and[15]where(1.11)is the adopted form for their analysis. These equations come with the initial data prescription

where u0denotes the initial velocity vector field.We also require that the velocity and the pressure satisfy

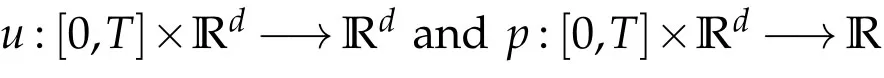
Before proceeding further,let us clarify some expressions involved in the momentum equation(1.11).Recall that u is divergence free.Then,in the distributional sense,the i component of the convective term(u·∇)v is defined by

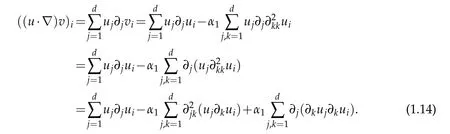
Analogously the i component(i.e.the partial derivative)ofcan explicitly be written as

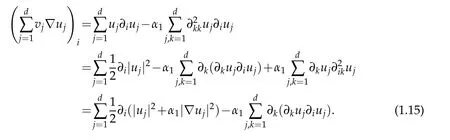
Therefore(1.11)can be differently expressed in the following form

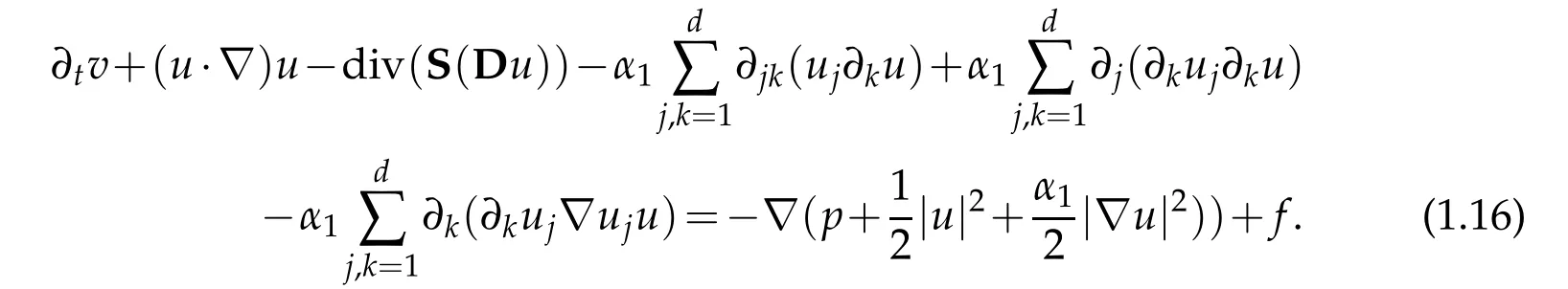
The rest of the paper is planed as follows.In Section 2,we introduce notations and functions spaces.We also outline some technical results that will be used later.In Section 3,we set up the assumptions imposed on the stress tensor S.Moreover,we present the resulted properties that will allow us to prove our main result.We also give a brief explanation of the studied problem and the considered type of viscosities.Later,we state the main theorem and relate it with some previous results that are concerned with the classical second grade fluids and those with shear-rate dependent viscosities.In Section 4,we give the proof of the existence part of our result.Finally,in Section 5 we show the uniqueness of the constructed solution.

The main feature of the proof is based on a construction of a sequence of approximated solutions using a discretization in space of Galerkin’s type and a limit process using compactness arguments in order to control the nonlinear terms.In addition,we will also make sense of the weak formulation introduced in the main theorem and conclude by showing that such a solution is unique via Gronwall’s lemma.

2 Notations and auxiliary results

Given a Banach space X(Ω)then X(Ω)stands for its dual space.We will not distinguishbetweenspaces of scalar,vectorand tensorvalued functions as one can easily makedifference of sense between them.We denote by Lq(0;T;X(Ω))the usual Bochner space consisting of functions which values are in X and are Lqtime-integrable over(0,T)and by Lq′(0,T;X∗(Ω))its dual where q′is the conjugate exponent of q given by q′=q/(q-1). On the other hand,C([0,T];X(Ω))stands for the space of continuous in time functions in[0,T]and with values in X.We also denote by Cw(0,T;X(Ω))the space of functions u which are in L∞(0,T;X(Ω))and continue for almost every t∈[0,T]for the weak topology of X(Ω).

Throughoutthe paper,if we denoteby c apositive constantwithneitherany subscript nor superscript then c is considered as a generic constant whose value can change from line to line in the inequalities and dependsonthe parameters in questionbut has no effect on the solution.On the other hand,we will denote in a bold character tensor functions and in the usual one vector valued and scalar functions.

In the sequel of this section,we review some technical results and classical lemmas on compactness arguments and limiting process.

Since we are dealing with space periodic and divergence-free vector fields,one can enjoy some special identities that will be summarized in the following lemma.

主体要素是以国家司法机关、行政机关为主的全社会力量。要求发动组织和全社会的人关心和参与治理犯罪。［5］科技是总体国家安全观重点涉及的领域，高新技术犯罪将会给国家安全造成巨大隐患。只有动员全社会的力量才能切实有力的预防此类犯罪，使危害国家安全者无处藏身，危害国家安全的行为无法得逞。［6］践行总体国家安全观有利于凝聚预防人工智能犯罪的磅礴力量，构筑起多元主体参与的犯罪预防体系。众人拾柴火焰高，相关主体应积极行动起来，为构筑起多元主体参与的犯罪预防体系添砖加瓦。

Lemma 2.1.Let f:Ω-→R and u,v:Ω-→Rdbe periodic functions.Suppose that u and v are divergence-free,then the following identities hold

Proof.The proof is based on the use of Green’s formula,the divergence-free propertyand the fact that boundary terms vanish due to the periodicity.For details,one can see[17, Lemma 2.9].

The famous Aubin-Lions lemma will play an important role in the sequel.

Lemma2.2(Aubin-Lions).Let 1＜α＜∞,1≤β≤∞and X0,X1,X2beBanach reflexive separable spaces such that

Then

Here,thesymbol→→standsforthecompact imbeddingwhile→forthecontinuous one.Lemma2.2is a generalversionoftheAubin-Lionslemma valid underthefulfillment of the assumption β=1 and is proved in[18]and[19],separately.

Lemma 2.3(Vitali).Let Ω be a bounded domain in Rdand fn:Ω-→R be a sequence of functions.Suppose that

•for all ε＞0,there exists δ＞0 such that

Then

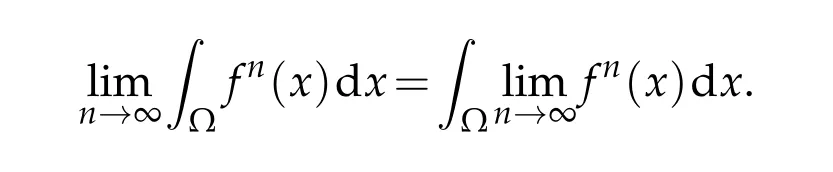
We would like to note that the second assumption stated in the lemma above expresses the equi-integrability of the sequence{fn}.Recall that if{fn}is uniformly bounded in some Lebesgue spaces Lq(Ω)for q＞1 then they are equi-integrable functions.

We finish this section by the Korn’s inequality whose a proof can be found in[17, Theorem 1.10].

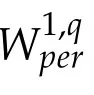
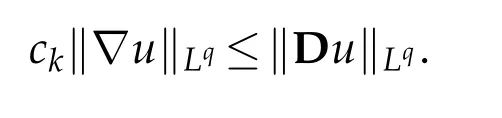
3 Assumptions and main results

Since we consider a variable viscosity depending on the shear rate,this makes the problem strongly nonlinear and brings some complications to its analysis.To deal with this situation,it seems naturally to impose further restrictions on the structure of the stress tensor S.

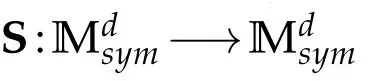
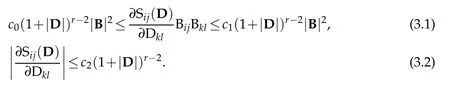
It is worth noticing that the nonlinearity of the tensor S has some useful properties that follows from(3.1)and(3.2).

Lemma 3.1.Let r∈(2,∞)be a fixed real number and the tensor S satisfy the assumptions(3.1) and(3.2).Then,there exist positive constants c3and c4such that,for all

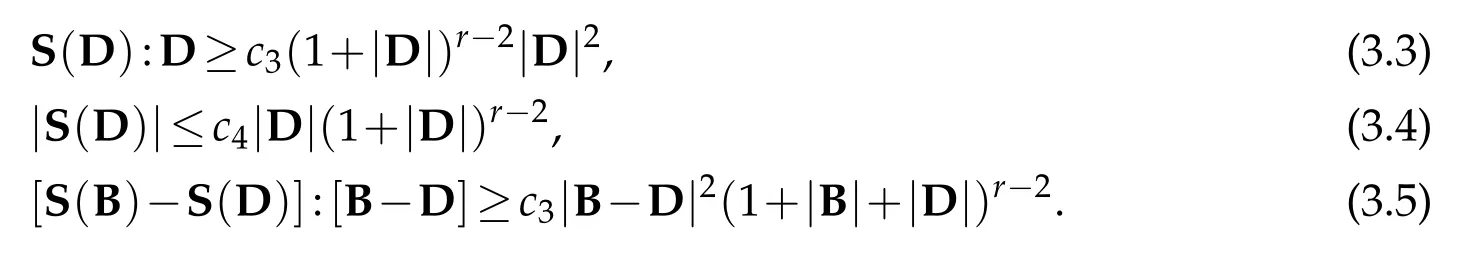
Proof.See[17,Lemma 1.19].

According to this lemma,the inequalities(3.3)and(3.4)express respectively the rcoercivity and the polynomial growth of the tensor S while(3.5)describes the strict monotonicity of this operator.To be more precise,one can give a typical example of stress tensors,where the above structure is satisfied,for example

whereµ0andµ1are positive constants.The models(3.6)constitutea large family ofstress tensors but do not include the proposed model(µ|D|r-2D)by Man and Sun in[8]and later by Man[7].The main results of ourpaperare summarized in thefollowing theorem.

Theorem 3.1.Let r∈[3,∞)and let the stress tensor S verify the assumptions(3.1)and(3.2).

Then there exists a strong solution u to the problem(1.11)-(1.13)such that

and satisfying the following weak formulation

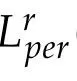
ii)The existence of the pressure can be deduced,with the help of the De Rham’s theorem,from the weak formulation(3.7)and one can assert that there is some distribution p such that(1.11)holds in[0,T]×Rd.

To the best of our knowledge,the question of existence of weak or strong solutions has not been raised for the class of generalized second grade fluids.Furthermore,this work seems to be the first to prove global existence and uniqueness of strong solution without restrictive smallness assumptions on the initial data.

Let us come back to some related results concerning classical second grade fluids whose Cauchy stress is described by the formula(1.1).In[20],Galdi and Sequeiraproved existence and uniqueness of global in time classical solution when the initial data is very small in a bounded regular domain of R3and subject to Dirichlet boundary conditions. Later,Le Rouxin[21]extendedthese results undersuitable regularity and growthrestrictions on the initial data with nonlinear partial slip boundary conditions in a bounded simply-connected domain.We also mention that Cioranescu and Ouazar[22]proved, for the Dirichlet boundary conditions case,existence and uniqueness of W3,2solutions that are global in two dimensions of spaces and local for small data in three dimensions. Further,Cioranescu and Girault[23]improved the three dimensional result by showing global existence under further appropriate assumptions on the data.On the other hand, Bresch and Lemoine[24]established existence and uniqueness of W2,r(r＞3)stationary solution for three dimensional bounded domain of classC2with smallness restrictions on the kinematic viscosityµand the forcing term.

The first results concerning unsteady incompressible flows of Navier-Stokes equations with shear rate dependent material coefficients go back to Ladyzhenskaya[25]and Lions[26],who proved for r≥3d/(d+2)the existence of weak solutions by using the monotone operator theory and compactness arguments.In the last two decades,the mathematical analysis of fluids with shear rate dependent viscosities have known a lot of relevant works dealing with existence of weak and strong solutions and regularity results.One can cite some leaders in this field such as M.Bul´ıˇcek,E.Feireisl,J.Frehse,J. M´alek,J.Neˇcas,K.R.Rajagopal,M.R˙u˘ziˇcka and many others and we refer to[2,3,27] where overviews of theses results are established.

In this work,we prove global in time existence of strong solution(in W1,r,r≥3),for spatially periodic two and three-dimensional flows and for a large class of fluids of second grade with shear rate dependent viscosities.Moreover,in a second part we prove uniqueness of such solution.All our results hold without restricting on the size of theinitial data.

The scheme of the proof is based on the use of Galerkin method.First,we construct the Galerkin approximations(based on the eigenfunctions of the Stokes operator)of the velocity and derive a priori W1,2-estimates.But this is not enough to ensure the convergence of nonlinear terms.That is why we have to look for new estimates of higher derivatives order.More precisely,we derive the crucial estimates that are sufficient to establish the compactness of the velocity gradient for the approximations.

Unlike the classical fluids of third grade,where in the W1,2and W2,2a priori estimates (established in a good way),one benefits from the presence of the term div(|Du|2Du) which has a regularizing effect,this term is absent from the momentum equation of the classical second grade fluids.For this reason there are no existence results of W2,2solutions for the last cited fluid but only W3,2solutions.In our case,one takes advantage from the coercivity of the stress tensor which will allow us to get W1,ra priori estimates in a first step and help us in the absorption operation in order to obtain W2,2estimates.

4 Existence of strong solutions

4.1 Existence of approximate solutions

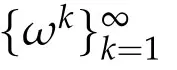
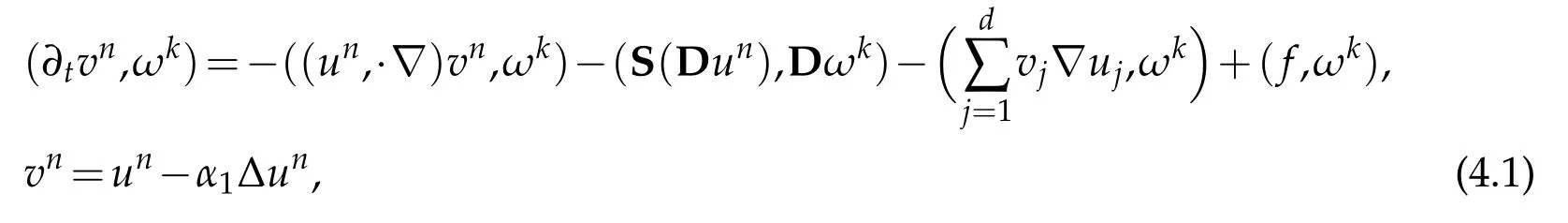
for all k=1,…,n.

To close the system(4.1),we prescribe the initial data as

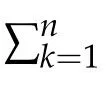
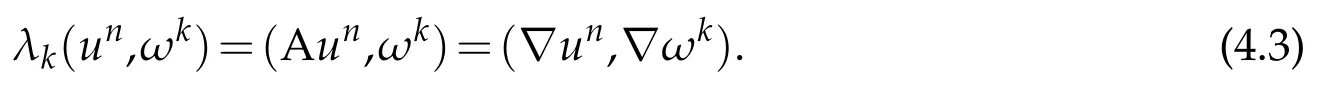
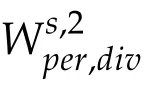
Due to the continuity of the right hand side of(4.1),the local existence of a solution to(4.1)-(4.2)on a short time interval(0,t∗)follows from the Carath´edory theory(see[29] for instance).In order to extend the solution to the whole time interval[0,T],we need to show that the solution remains finite for all positive times which consequently implies that t∗=T.To achieve this goal,we will derive some uniform estimates.

Multiplying the k-th equationin(4.1)by(t)and summing over k=1,…,n,we obtain the following energy equality

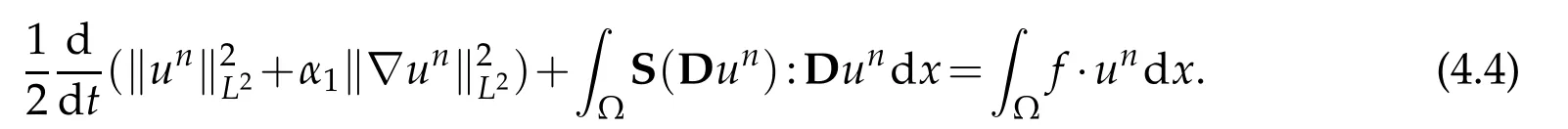
All the other nonlinear terms vanish,it is due to the incompressibility constraint divωk= 0,see the identities(2.1)and(2.2).

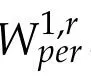
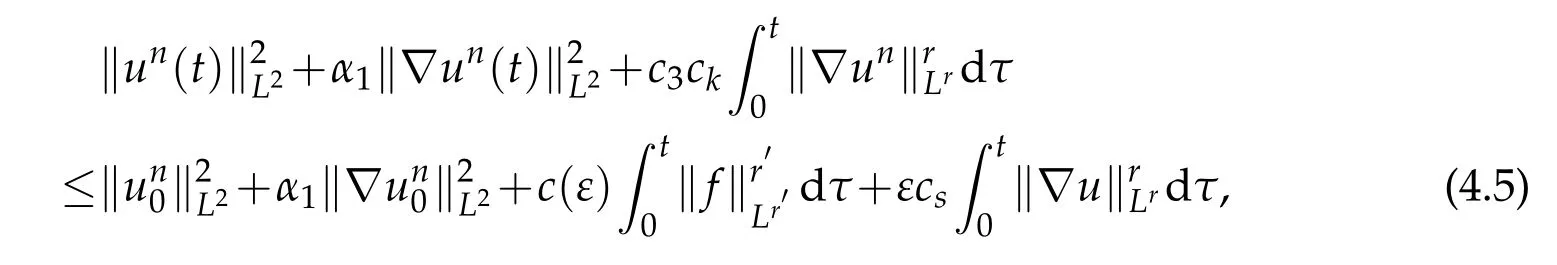
Choosing ε small enough,we obtain the following uniform bounds for all t∈(0,T)

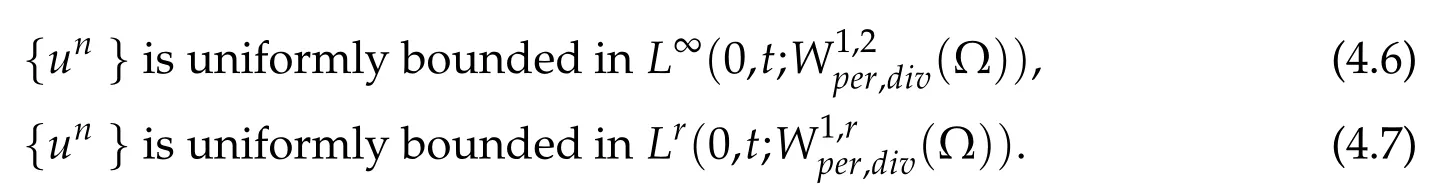
From(4.6)it follows that

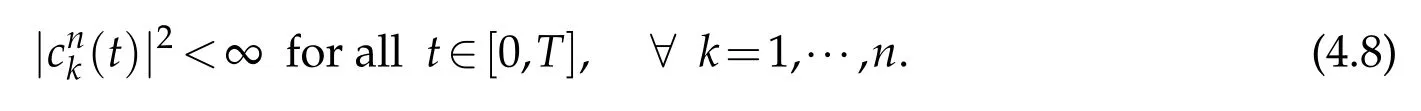
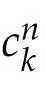
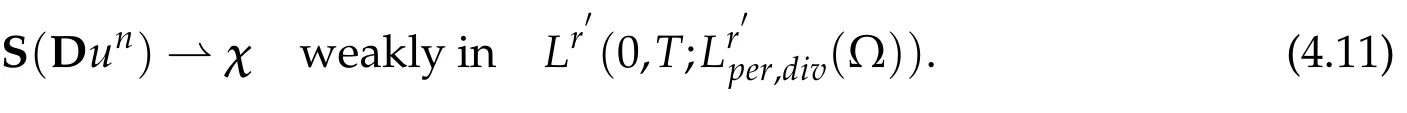
The main difficulty in the limiting process consists in the terms which are nonlinear in∇unand more precisely those with product of spatial derivative of first order.So we are urged to obtain stronger regularity results on the sequence{un}in order to have compactness of the sequence{∇un},and thus consequently the pointwise convergence. The next paragraph will focus on.

4.2 Compactness and limiting process

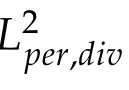
In the following,we will estimate appropriately the different terms appearing in(4.12). Using(3.1)and(3.3)we get from the stress tensor

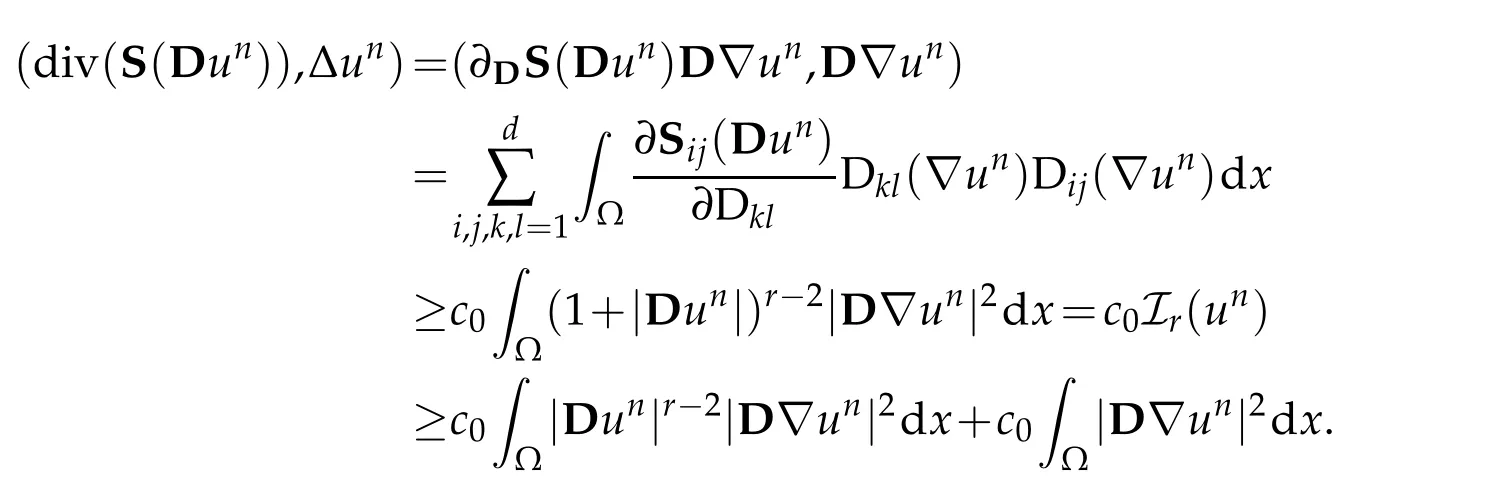
By Korn’s inequality(2.4),we deduce that

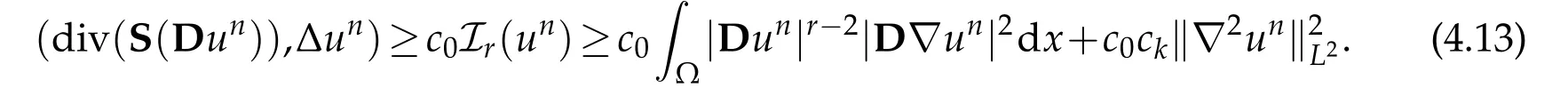
Furthermore,we recall that the quantity

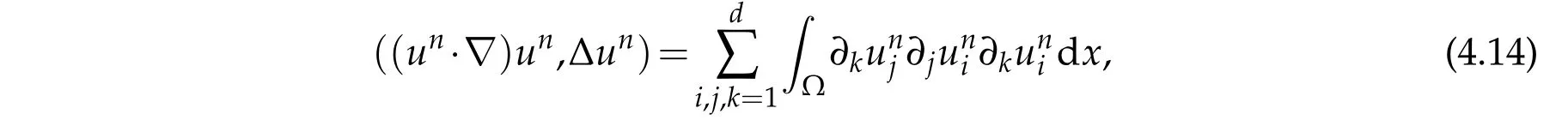
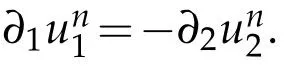
Using integration by parts and the divergence-free condition of un,we see from(1.14) and(2.1)that we have

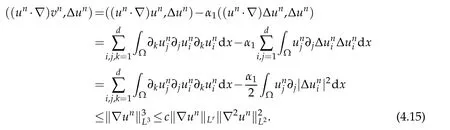
On the other hand,one can deduce from(1.15)that

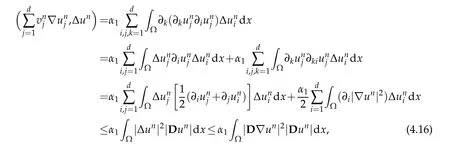
where in the third line of the last estimate we have used the symmetry of the scripts i and j.If r＞3 then by means of the Young’s inequality,one have

which yields that

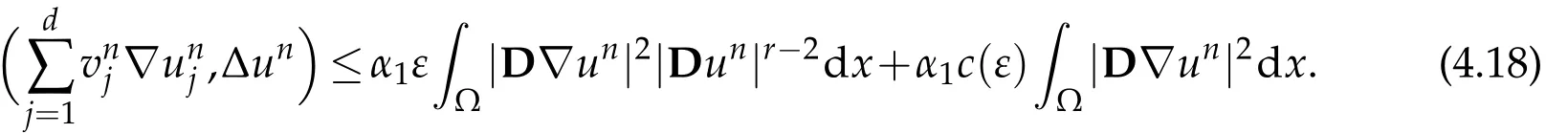
Putting all the estimates(4.13),(4.16)and(4.18)together,the energy inequality(4.12) becomes

Choosing ε≪1 small enough in such a way that α1ε＜c0one can absorb the first term of the right hand side of(4.19)and find that

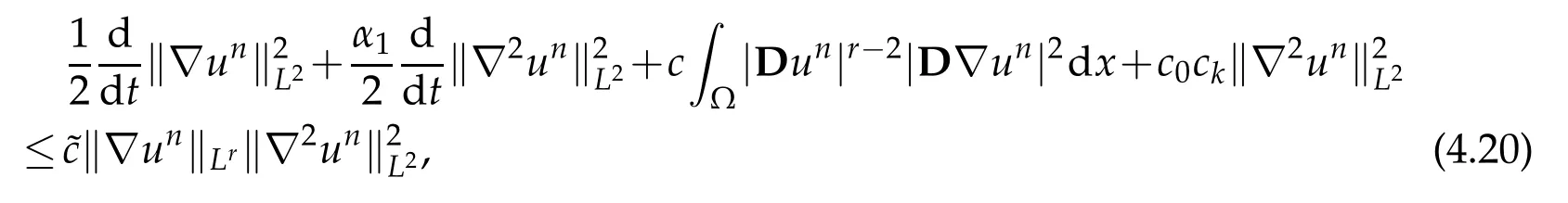
where c and˜c are some positive fixed constants.Note that for r=3,we do not need to use(4.17)and inequality(4.20)remains valid.Consequently,sincek∇unkLr+kfkL2is uniformly bounded in L1(0,T),the Gronwall’s lemma enables us to conclude for both cases d=2 and d=3 that

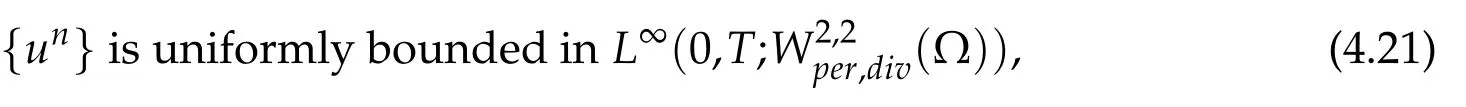
and that for all n

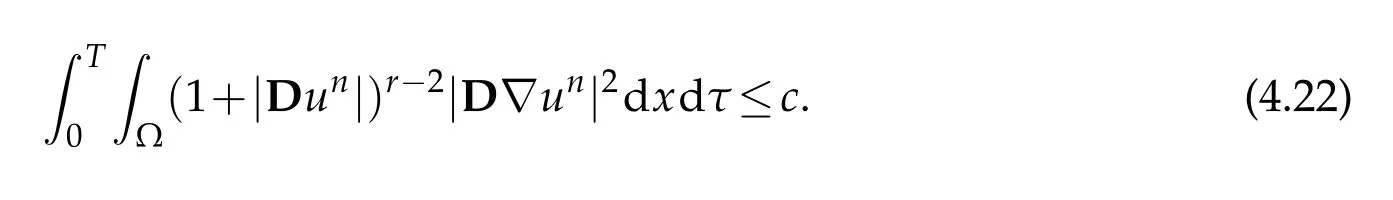
Thus,we have

In order to prove a compactness for the velocity field in some Sovolev spaces,we need uniform estimates for the time derivative∂tun.To do this,observe that for test function

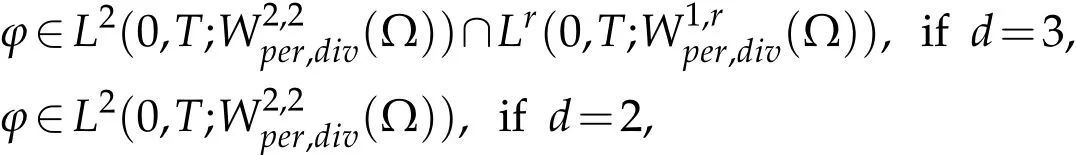
we have

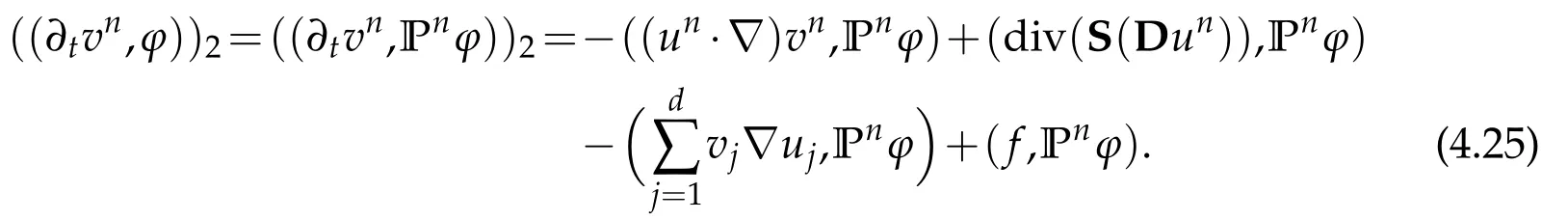
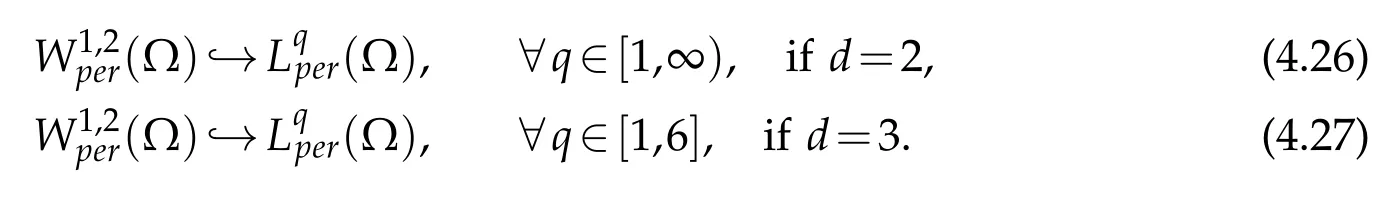
Moreover,it is obvious that

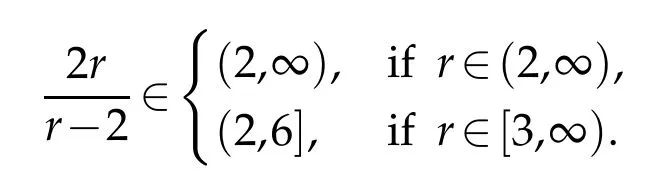
Therefore,by(1.14)and the H¨older’s inequality,we obtain

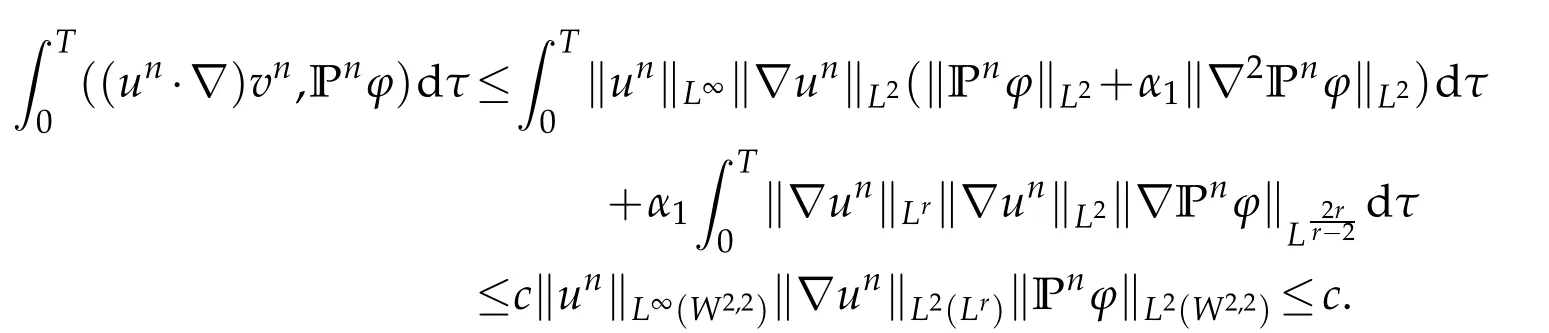
Similarly,using(1.15)and taking into account the divergence-free condition,we get

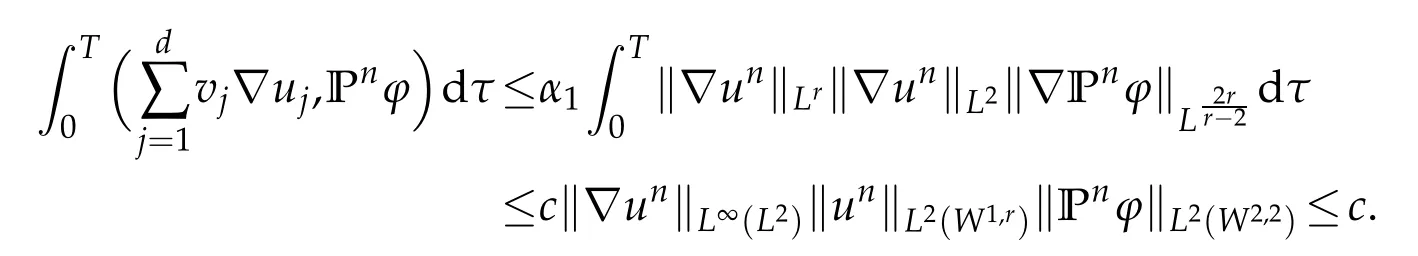
To conclude,we consider now the stress tensorterm.Thanks to the growthproperty(3.4) we have

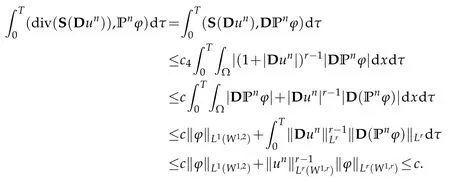
In dimension two we can improve,thanks to(4.26),the last estimate as follows

Now,denoting by

and keeping in mind the last estimates,we infer that

and hence by the classical elliptic regularity we deduce that

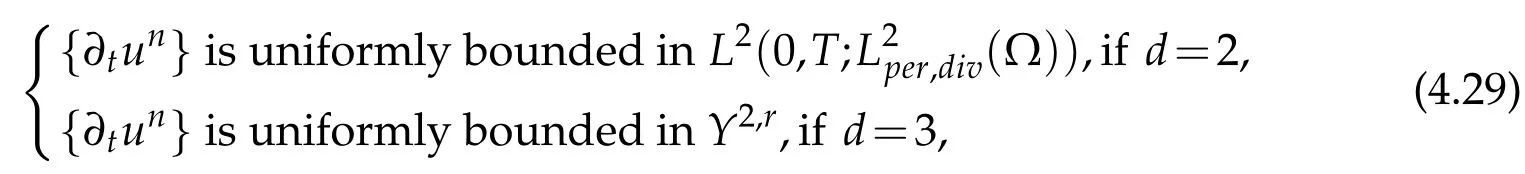
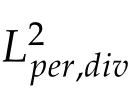
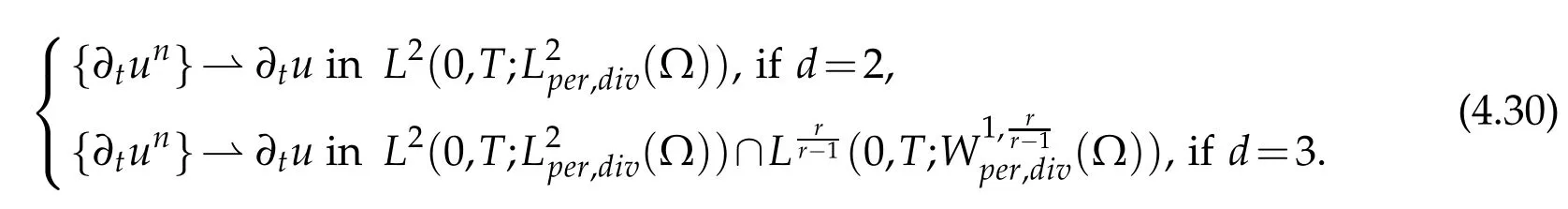
Since the power r lies in[3,∞)then r/(r-1)∈(1,3/2].So,by the Aubin-Lions Lemma 2.2,(4.7)and(4.30),we deduce that

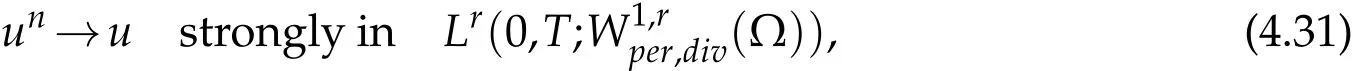
which implies that

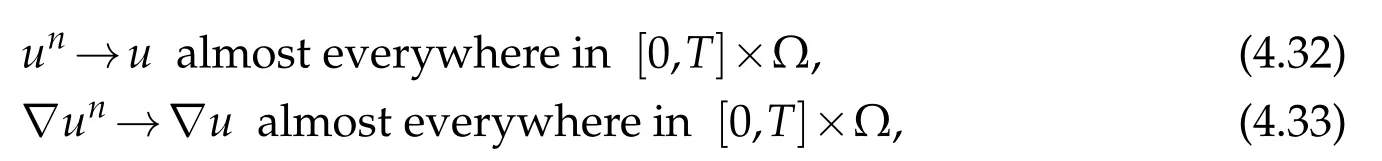
and by symmetry

Since the stress tensor S is continuous

Consequently,by means of Vitali’s lemma we deduce that χ=S(Du)and one have

and almost everywhere in[0,T]×Ω.

Now we outline the passage to the limit in the weak formulation(3.7).Using(4.28) and(4.29),we can pass to the limit in the terms corresponding to the time derivative for Δu and u,respectively.On the other hand,the limiting process in the convective terms involving(1.14)and(1.15)and the stress tensor are ensured by(4.31),(4.31)and(4.36).

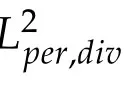
Concerning the weak continuity,it is easy to show

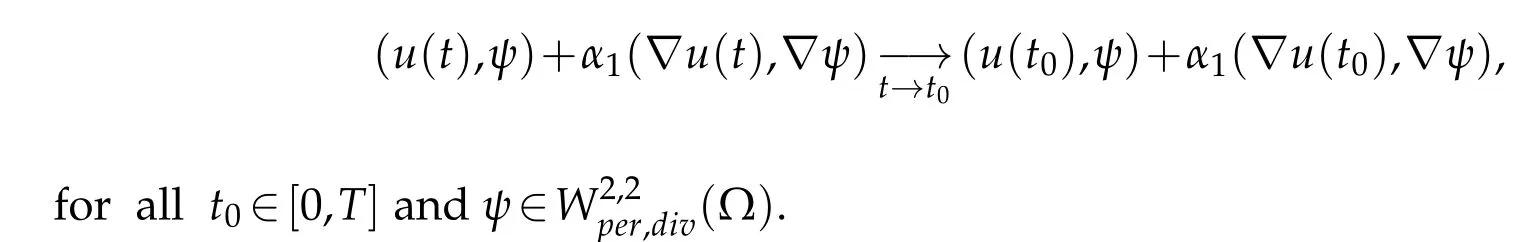
To finish this section,we can easily handle the attainment of the initial data.For more details one can consult paragraph 3.10 in[2].

5 Uniqueness of strong solution

Consider u and¯u(with initial data u0and¯u0respectively)two strong solutions to the problem consisting of Eqs.(1.10)-(1.13)as defined in Theorem 3.1.We set w:=u-¯u their difference.Subtracting the equations relatively to u and¯u we obtain the following system

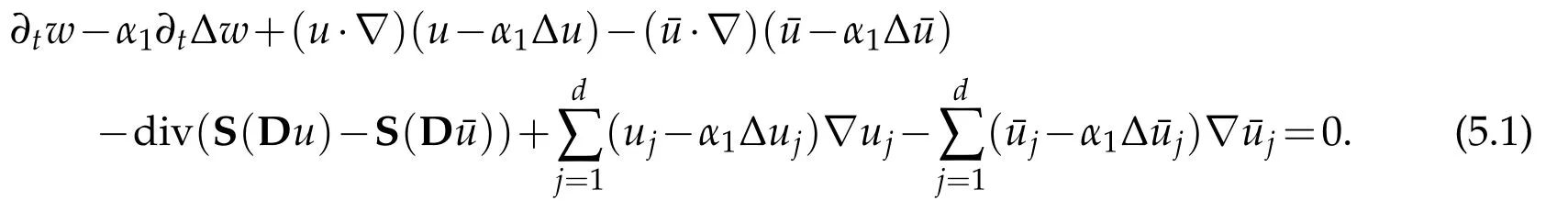
Multiplying(5.1)by w and integrating over Ω,we obtain by(3.5)the following energy inequality

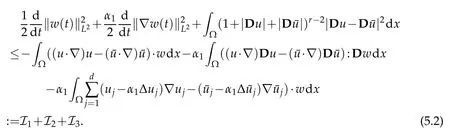
The first term of the right hand side of(5.2)can be handled in the following way

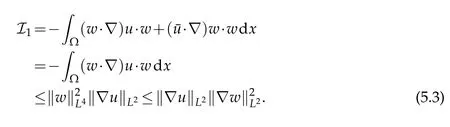
Next,we deal with the last term in(5.2).Using(1.15),we have

By symmetry and integration by parts,we get

In view of all these estimates,we have

where F(u,¯u,w)is a function incorporating

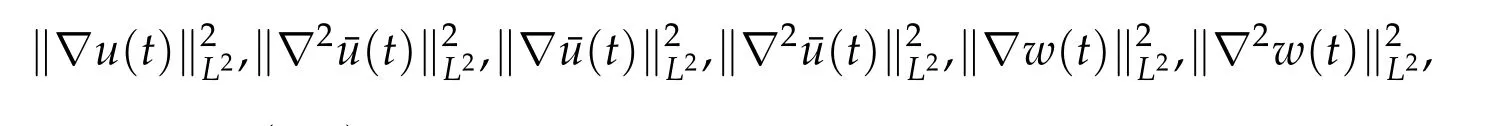
and belonging to L∞(0,T).Therefore,we obtain

Finally,by Gronwall’s inequality we infer that

Acknowledgments

We are grateful to the anonymous referee for a careful reading of the manuscript and fruitful remarks and suggestions.

[4]Dunn J.E.,On the free energy and stability of nonlinear fluids.Journal of Rhealogy,26(1982), 43-68.

[5]Man C.S.,Shields D.H.,Kjartanson B.,Sun Q.K.,Creep of ice as a fluid of complexity 2:the pressuremeter problem.Proceedings of the 10thCanadian Congress of Applied Mechanics, The University of Western Ontario,London,1985.

[6]Kjartanson B.H.,Shields D.H.,Domaschuk L.,Man C.S.,Creep of ice measured with the pressuremeter.Canadian Geotechnical Journal,25(1988),250-261.

[7]Man C.S.,Nonsteady channel flow of ice as a modified second-order fluid with power-law viscosity.Arch.Ration.Mech.Anal.,119(1992),35-57.

[8]Man C.S.,Sun Q.K.,On the significance of normal stress effects in the flow of glaciers.J. Glaciology,33(1987),268-273.

[9]Man C.S.,Massoudi M.,On the thermodynamics of some generalized second-grade fluids. Continuum Mech.Thermodyn.,22(2010),27-46.

[10]MassoudiM.,VaidyaA.,On some generalisations of thesecond gradefluid model.Nonlinear Anal.RWA,9(2008),1169-1183.

[11]Rajagopal K.R.,On the creeping flow of the second order fluid.J.Non-Newton.Fluid Mech., 15(1984),239-246.

[12]Busuioc V.,On second grade fluids with vanishing viscosity.Portugaliae Mathematica,59 (2002),47-65.

[13]Busuioc V.,Sur quelques problmes en mcanique des fluides non newtoniens.Ph.D.thesis, Universitde Piere et Marie Curie(Paris 6),2000.

[14]Busuioc V.,Iftimie D.,Lopes Filho M.,Nussenzveig Lopes H.,Incompressible Euler as a limit of complex fluid models with Navier boundary conditions.J.Diff.Eqns.,252(2012), 624-640.

[15]Iftimie D.,Remarques sur la limite α→0 pour les fluides de grade 2.C.R.Acad.Sci.Paris Srie I Math.,334(2002),83-86.

[16]Massoudi M.,Phuoc T.X.,Unsteady motion of a non-linear viscoelastic fluid.Int.J.Non-Linear Mech.,44(2009),1063-1072.

[19]Simon J.,Compact sets in the space Lp(0,T;B).Annali di Matematica Pura et Applicata,146 (1987),65-96.

[20]Galdi G.P.,Sequeira A.,Further existence results for classical solutions of the equations of a second grade fluid.Arch.Ration.Mech.Anal.,128(1994),297-312.

[21]Le Roux C.,Existence and uniqueness of the flow of second-grade fluids with slip boundary conditions.Arch.Ration.Mech.Anal.,148(1999),309-356.

[22]CioranescuD.,OuazarE.H.,Existenceanduniqueness forfluids ofsecond grade.InNonlinear Partial Differential Equations and Their Applications(Collge de France Seminar,Paris, 1982/1983),4,Boston,178-197.

[23]Cioranescu D.,Girault V.,Weak and classical solutions of a family of second grade fluids. Int.J.Non-Linear Mech.,32(1997),317-35.

[24]Bresch D.,Lemoine J.,Sur l’existence et l’unicitde solution des fuides de grade 2 ou 3.C. R.Acad.Sci.Paris,srie I,324(1997),605-610.

[25]Ladyzhenskaya O.A.,The Mathematical Theory of Viscous Incompressible Flow.Gordon and Breach,New York,1969.

[29]Zeidler E.,Nonlinear Functional Analysis and its Applications.Springer-Verlag,New York, 1990.

[30]Adams R.A.,Sobolev Spaces.Academic Press,New York-San Francisco-London,1975.

10.4208/jpde.v27.n2.1 June 2014

∗Corresponding author.Email addresses:hafedh.bousbih@gmail.com(H.Bousbih),mohamed.majdoub@ fst.rnu.tn(M.Majdoub)

AMS Subject Classifications:76B03,35L60

Chinese Library Classifications:O175.22,O175.27