Global Well-Posedness of Classical Solutions with LargeInitialDatatotheTwo-DimensionalIsentropic Compressible Navier-Stokes Equations

ZHANG Peixin,DENG Xuemeiand ZHAO Junning1School of Mathematical Sciences,Huaqiao University,Quanzhou 3601,China.

1School of Mathematical Sciences,Xiamen University,Xiamen 361005,China.

Global Well-Posedness of Classical Solutions with LargeInitialDatatotheTwo-DimensionalIsentropic Compressible Navier-Stokes Equations

ZHANG Peixin1,2,∗,DENG Xuemei2and ZHAO Junning21School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China.

1School of Mathematical Sciences,Xiamen University,Xiamen 361005,China.

Received 25 April 2013;Accepted 28 February 2014

.We establish the global existence and uniqueness of classical solutions to the Cauchy problem for the two-dimensional isentropic compressible Navier-Stokes equations with smooth initial data under the assumption that the viscosity coefficient µis large enough.Here we do not require that the initial data is small.

Isentropic compressible Navier-Stokes equations;large viscosity coefficient;global classical solutions.

1 Introduction

In this paper,we consider the following compressible Navier-Stokes equations in R2

where ρ,u=(u1,u2)and P=Aργ(A＞0,γ＞1)are the fluid density,velocity and pressure, respectively.The constant viscosity coefficientsµand λ satisfy the physical restrictions:

Let˜ρ be a fixed positive constant.We look for the solutions,(ρ(x,t),u(x,t)),to the Cauchy problem for(1.1)with the far field behavior:

and initial data,

There are huge literature on the large time existence and behavior of solutions to (1.1).The one-dimensional problem has been studied by many people,see[1–4]and the references therein.For the multi-dimensional case,the local existence and uniqueness of classical solutions are known in the absence of vacuum(see[5,6]),for strong solutions and the case that the initial density need not be positive and may vanish in an open sets see[7–10].The global classical solutions were first obtained by Matsumura-Nishida[11] for the initial data close to a non-vacuum equilibrium in the sense of some Sobolev space Hs.Later,Hoff[12,13]studied the problem for discontinuous initial data.The existence of weak solutions with arbitrary initial data was studied(the far field is vacuum,that is˜ρ=0)by Lions[14](see also Feireisl[15]),where he obtains the global existence of weak solutions-defined as solutions with finite energy when the exponent γ is suitably large.The main restriction on initial data is that the initial energy is finite,so that the density vanishes at far fields,or even has compact support.Zhang and Fang established the existence of the global weak solutions in R2with the small initial energy of the initial data and the initial density bounded away from zero(see[16]).Recently,Huang-Li-Xin[17]establish the existence of the global classical solutions to the Cauchy problem for thecompressible Navier-Stokes equationsin 3-D withsmoothinitial data which are small energy.By theinspirationof[17],weestablishthe global existenceof classical solutionsto the Cauchy problem to the 3-D compressible Navier-Stokes equations with general initial data under the assumption that the viscosity coefficientµis large enough(see[18]).

Note that the Gagliardo-Nirenberg-Sobolev inequality in R2is different from the Gagliardo-Nirenberg-SobolevinequalityinR3,forexample,kukL6≤Ck∇ukL2inR3which is a base of the proof in[18],but it is not correct in R2.So the result in[18]can not include the two-dimensional case.In this paper we generalized the result in[18]to the twodimensional case,to study the global existence of classical solutions to Cauchy problem (1.1)for general initial data.We obtain the well-posednessof global classical solutions for large initial data,under the assumption that the viscosity coefficientµis large enough. Here we do not require that the initial energy is small.In this paper some new difficulties are overcame.

Beforestatingthemainresults,weexplainthenotationsandconventionsusedthroughout this paper.We denote

For 1≤r≤∞,we denote the standard homogeneous and inhomogeneous Sobolev

spaces as follows:

The initial energy is defined as follows:

where G denotes the potential energy density given by

It is easy to see

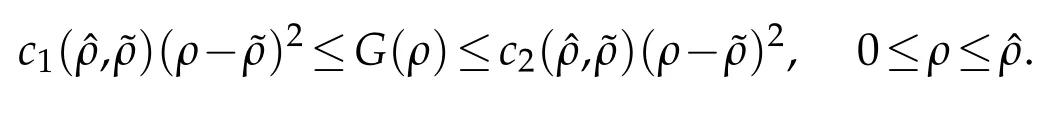
Set N0=λ/µ.Then(1.2)implies N0≥-1 and

The main result in this paper can be stated as follows:

Theorem 1.1.Assume that(1.2)hold.For given positive numbers M1and M2(not necessarily small)andˆρ≥˜ρ+1,suppose that the initial data(ρ0,u0)satisfy

and the compatibility condition

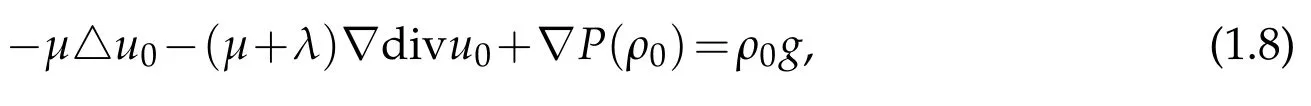
the Cauchy problem(1.1),(1.3)-(1.4)has a unique global classical solution(ρ,u)satisfying for any 0＜τ＜T＜∞,

and

Moreover,the following large-time behavior holds

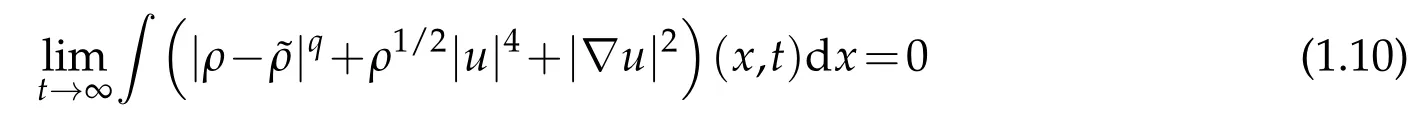
for all q∈(2,∞).

Remark 1.1.It is easy to show that the solution obtained in Theorem 1.1 is a classical solution for positive time.

Remark 1.2.In Theorem 1.1,for simplicity of the description,we assume onlyµis large enough,in fact we can give a quantity estimate for the viscosity coefficientsµfrom the proof of Theorem 1.1.

Remark 1.3.Similar to the Serrin type blow-up criterion for 3-D compressible Navier-Stokes equations(see[19]),there exists the same type blow-up criterion in R2,to prove the existence of the global solutions,we need only to prove that density ρ is uniformly bounded to all t≥0.

The rest of the paper is organized as follows:In Section 2,we state some elementary facts and inequalities which will be needed in later analysis.Section 3 is devoted to deriving the necessary a priori estimates on classical solutions which are needed to extend the local existence of solution to all the time.

2 Preliminaries

In this section,we will recall some known facts and elementary inequalities which will be used frequently later.

Lemma 2.1([20]).Assume that the initial data(ρ0,u0)with ρ0≥0 satisfy(1.7)-(1.8)and˜ρ＞0. Then there exist a small time T∗＞0 and a unique classical solution(ρ,u)to the Cauchy problem (1.1),(1.3)-(1.4)such that for any 0＜τ＜T∗,

Next,the following well-known Gagliardo-Nirenberg inequality will be used later frequently.

Lemma 2.2.For p∈[2,+∞),q∈(1,∞),and r∈(2,∞),there exists some constant C＞0,which may depend on p,q,r,such that for f∈H1and g∈Lq∩D1,r,we have

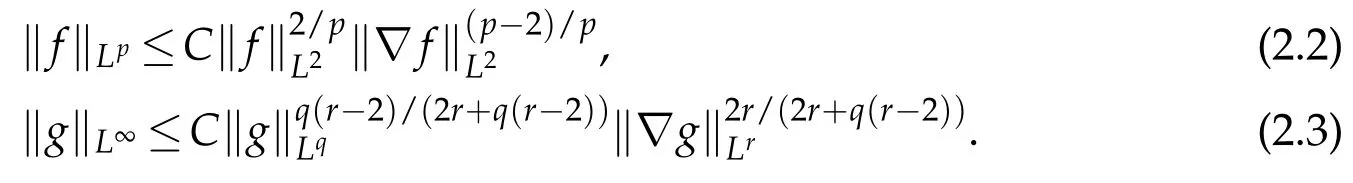
We now state some elementary estimates which follow from Gagliardo-Nirenberg inequalities and the standard Lp-estimate for the following elliptic system derived from the momentum equations in(1.1)

where

are the material derivative of f,the effective viscous flux and the vorticity respectively, here and after

Lemma 2.3.Let(ρ,u)be a smooth solution of(1.1)and(1.3).Then there exists a generic positive constant C such that for any p∈[2,+∞),

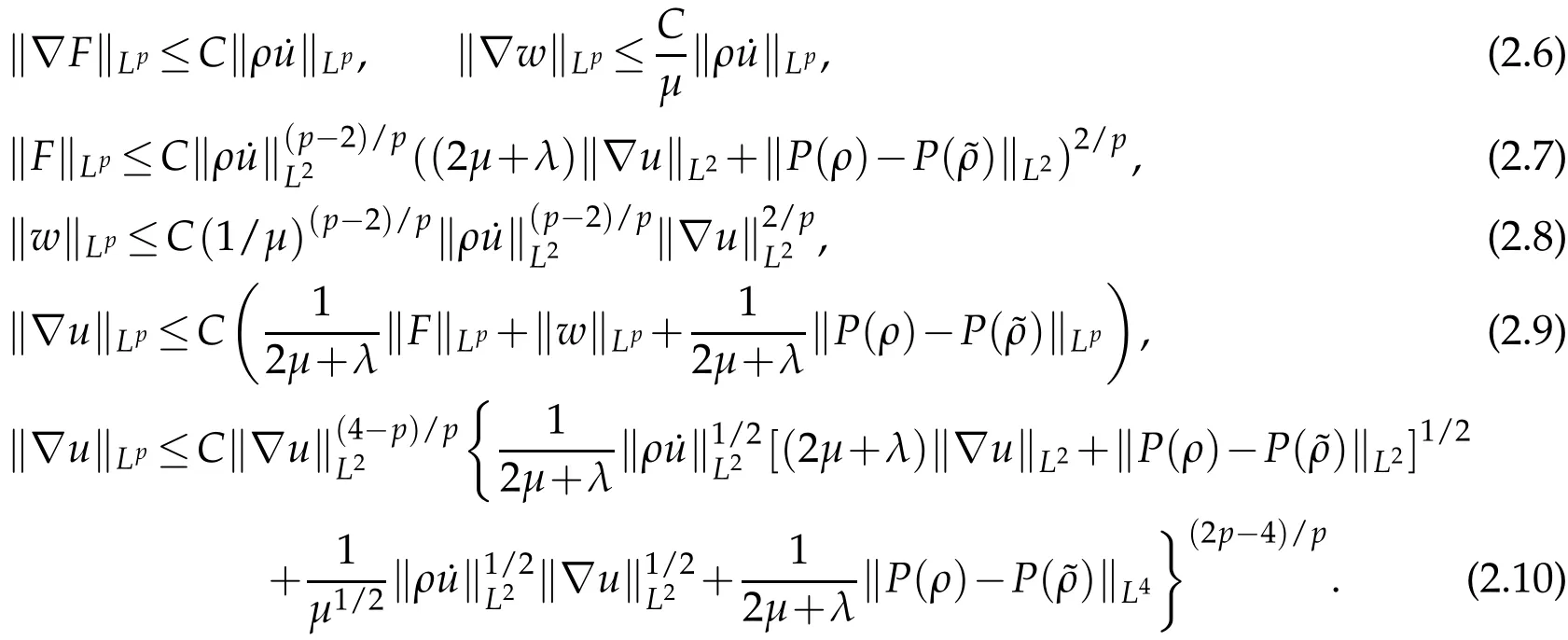
Proof.The standard Lp-estimate for the elliptic system(2.4)yields directly(2.6),which together with(2.2)and(2.5)gives(2.7)and(2.8).

Note that-△u=-∇divu+∇×w,which implies that

Thus the standard Lp-estimates shows that

By the H¨older inequality,(2.2),(2.6)-(2.8),one has

This finishes the proof of Lemma 2.3.

Next,the following Zlotnik inequality will be used to get the uniform(in time)upper bound of the density ρ.

Lemma 2.4([21]).Let the function y satisfy

with g∈C(R)and y,b∈W1,1(0,T).If g(∞)=-∞and

for all 0≤t1＜t2≤T with someN0≥0 andN1≥0,then

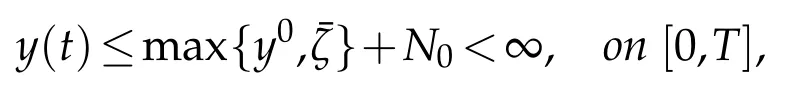
3 A priori estimates

In this section,we will establish some necessary a priori bounds for smooth solutions to the Cauchy problem for(1.1),(1.3)-(1.4)to extend the local classical solution guaranteed by Lemma 2.1.Thus,Let T＞0 be a fixed time and(ρ,u)be the smooth solution to(1.1),

(1.3)-(1.4),on R2×(0,T]in the class(2.1)with smooth initial data(ρ0,u0)satisfying(1.6)-(1.8).To estimate this solution,we define

语言知识与技能是学好商务英语的基础，对于商务英语专业的学生来说，在专门针对商务英语专业的考试推出之前，必须重视并通过英语专业四级、八级考试。据统计，2012年全国独立学院英语专业八级考试通过率不到三分之一，顺利通过专业四级考试是大多数学生更为现实的目标。因此，独立学院商务英语专业教学的重心应主要放在听、说、读、写技能培养和词汇、语法知识的讲授上。

We have the following key a priori estimates on(ρ,u).

Proposition 3.1.For given numbers M1,M2＞0(not necessarily small)andˆρ≥˜ρ+1,assume that(ρ0,u0)satisfy(1.6)-(1.8).Then there exist positive constants K1,K2such that if(ρ,u)is a smooth solution of(1.1),(1.3)-(1.4)on R2×(0,T]satisfying

the following estimates hold

provided that(1.9)holds.

Proof.Proposition 3.1 is an easy consequence of the following Lemmas 3.2,3.3 and 3.5.

Inthe following,we will use the conventionthat C denotesa genericpositive constant dependingon A,γ,C0,˜ρ,ˆρ andtheconstantsinsomeSobolev’sinequalities,and wewrite C(α)to emphasize that C depends on α.

We start with the following standard energy estimate for(ρ,u)and preliminary L2bounds for∇u and ρ˙u.

Lemma 3.1.Let(ρ,u)be a smooth solution of(1.1),(1.3)-(1.4)with 0≤ρ≤2ˆρ.Then there is a constant C such that

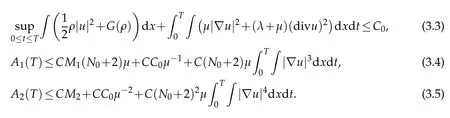
Proof.Multiplying the first equation of(1.1)by G′(ρ)and the second by ujand integrating,applying the far field condition(1.3),one shows easily the energy inequality(3.3).

Multiplying(1.1)2by˙u then integrating the resulting equality over R2leads to

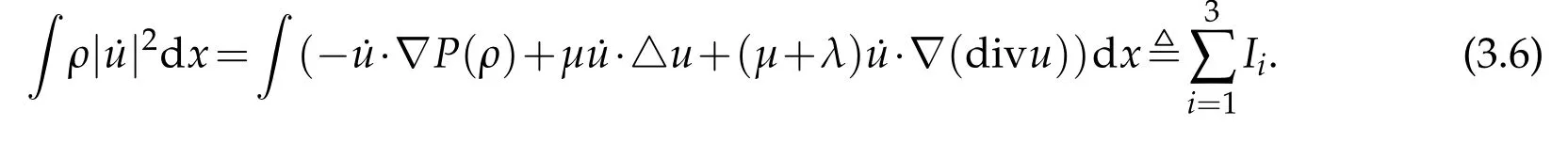
Using(1.1)1and integrating by parts give

Integrating by parts,we have

and similarly,

Collecting(3.7)-(3.9)into(3.6)leads to

where

Integrating(3.10)over(0,T),using(1.5)and(3.3),one has

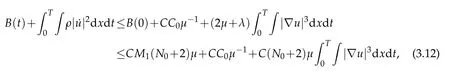
i.e.,(3.4)holds.

Integrating by parts and using the equation(1.1)1,we have

After integrating by parts,we have

Similarly,

Substituting(3.14)-(3.16)into(3.13)shows that for δ＞0 suitably small enough,

Integrating(3.17)over(0,T)gives

where we have used the compatibility condition(we can defineThus one finishes the proof of this Lemma.

Next,the following lemma will give more accurate estimates with respect to A1(T) and A2(T).

Lemma 3.2.There exist positive constants K1,K2depending on A,γ,C0,˜ρ,ˆρ,M1and M2such that,if(ρ,u)is a smooth solution of(1.1),(1.3)-(1.4)satisfying(3.1),then

providedµ≥C1(N0+2),whereC1is a constant depending only on A,γ,C0,˜ρ,ˆρ.

Proof.Using H¨older’s inequality and Young’s inequality,it follows from(3.3)and(3.4) that

Due to(2.9),

It follows from(2.7)that

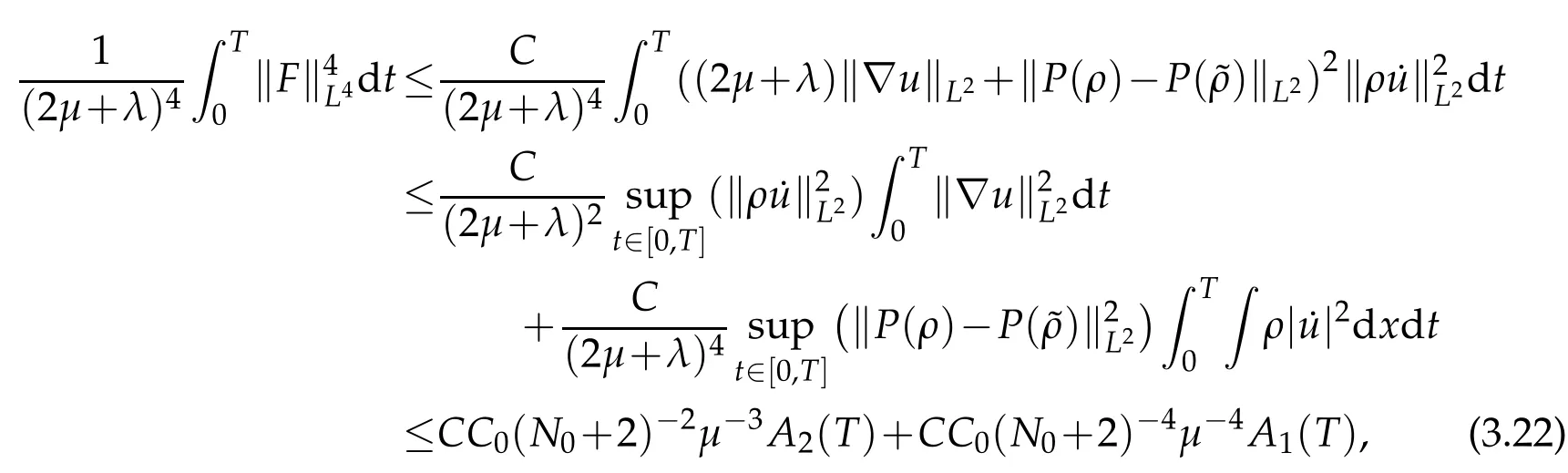
and duo to(2.8),

To estimate the second term on the right side of(3.21),one deduces from(1.1)that P(ρ)-P()satisfies

Multiplying(3.24)by 3(P(ρ)-P())2and integrating the resulting equality over R2,one gets after using divu=(2µ+λ)-1[F+P(ρ)-P()]that

Integrating(3.25)over(0,T),one may arrive at

Therefore,collecting(3.21)-(3.23)and(3.26)shows that

Combining(3.20)and(3.27)leads to

Clearly if choose K1such that

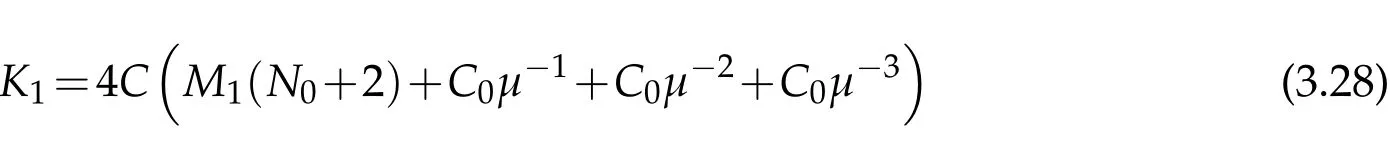
and

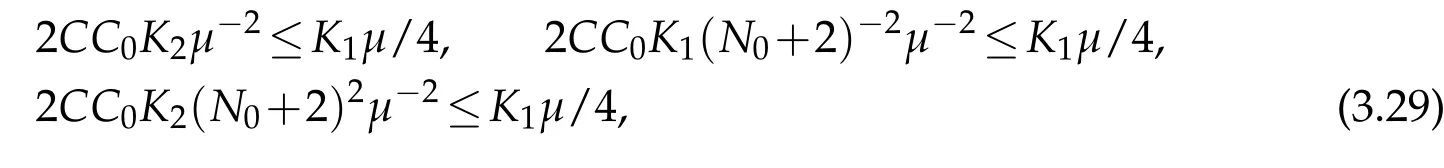
then the first inequality of(3.19)holds.

On the other hand,combining(3.5)and(3.27)gives

Clearly if choose K2such that

and

then the second inequality of(3.19)holds.

Combining(3.29)and(3.31),one has.

Lemma 3.3.Let t∈[0,T]and p∈[2,+∞),we have

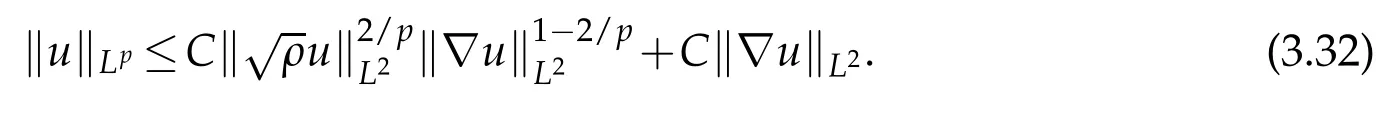
Proof.Since

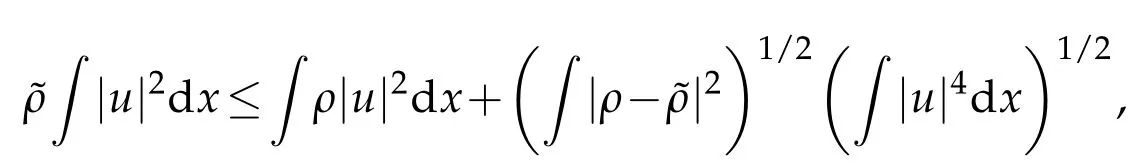
applying(2.2),(1.8)and(3.3),we get

Hence form(2.2)we obtain the inequality of(3.32).

We now proceed to derive uniform(in time)bounds for ρ.

Lemma 3.4.There exists a positive constantCdepending on C0,A,γ,,such that,if

and(ρ,u)is a smooth solution of(1.1),(1.3)-(1.4)as in Lemma 3.2,then

Proof.To prove this lemma,we rewrite the equation of the mass conservation(1.1)1as

where

For all 0≤t1≤t2≤T,one deduces from Lemma 2.2,(3.3),(3.19)and(2.10)that

where(3.28),(3.30),(3.33)and the following estimate is used,choosingCin(3.33)is suitably large.According to(2.6),(2.2)and(3.32),such that

Therefore,one can chooseN1andN0in(2.11)as:

Note that

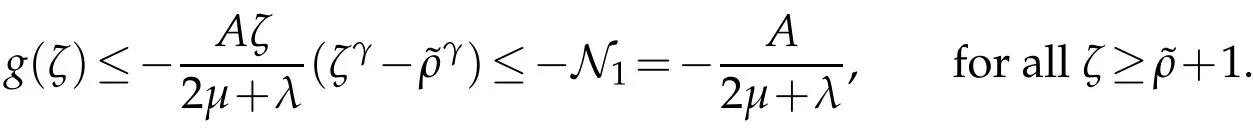
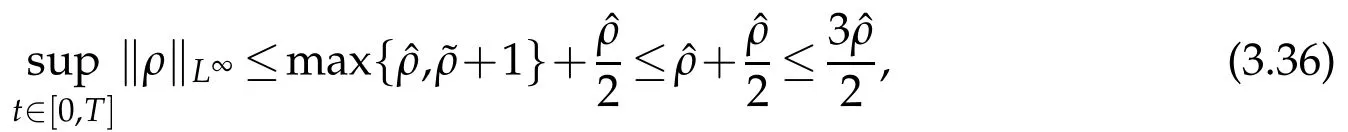
which completes the proof of this Lemma.

Proof of Theorem 1.1.Proposition 3.1 implies that the density ρ and A1,A2are uniformly boundedindependentof t.Hence according to the blow-up criterion for 2D compressible Navier-Stokes equations,which can be obtained easily by the method of[19],the Cauchy problem(1.1),(1.3)-(1.4)has a global classical solution.The large-time behavior of(ρ,u) in(1.10)can be proved in the same way as that in[17].?

Acknowledgments

This work was partially supported by National Natural Science Foundation of China (Grant No.11001090),the Fundamental Research Funds for the Central Universities (Grant No.11QZR16).

[1]Hoff D.,Global existence for 1D,compressible,isentropic Navier-Stokes equations with large initial data.Trans.Amer.Math.Soc.,303(1)(1987)169-181.

[2]Kazhikov A.V.,Shelukhin V.V.,Unique global solution with respect to time of initialboundary value problems for one-dimensional equations of a viscous gas.Prikl.Mat.Meh., 41(1977)282-291.

[3]SerreD.,Solutions faibles globales des´equations de Navier-Stokespour un fluide compressible.C.R.Acad.Sci.Paris S´er.I Math.,303(1986)639-642.

[4]Serre D.,Sur 1’´equation monodimensionnelle d’un fluide visqueux,compressible et conducteur de chaleur.C.R.Acad.Sci.Paris S´er.I Math.,303(1986)703-706.

[5]Nash J.,Le probl`eme de Cauchy pour les´equations diff´erentielles d’un fluide g´en´eral.Bull. Soc.Math.France,90(1962)487-497.

[6]SerrinJ.,On theuniqueness ofcompressiblefluid motion.Arch,Rational.Mech.Anal.,3(1959) 271-288.

[7]Cho Y.,Choe H.J.,Kim H.,Unique solvability of the initial boundary value problems for compressible viscous fluid.J.Math.Pures Appl.,83(2004)243-275.

[8]Cho Y.,Kim H.,On classical solutions of the compressible Navier-Stokes equations with nonnegative intial densities.Manuscript Math.,120(2006)91-129.

[9]Choe H.J.,Kim H.,Strong solutions of the Navier-Stokes equations for isentropic compressible fluids.J.Differ.Eqs.,190(2003)504-523.

[10]Salvi R.,Straskraba I.,Global existence for viscous compressible fluids and their behavior as t→∞.J.Fac.Sci.Univ.Tokyo Sect.IA.Math.,40(1993)17-51.

[11]Matsumura A.,Nishida T.,The initial value problem for the equations of motion of viscous and heat-conductive gases.J.Math.Kyoto Univ.,20(1)(1980)67-104.

[12]HoffD.,Global solutions of the Navier-Stokesequations for multidimendional compressible flow with disconstinuous initial data.J.Differ.Eqs.,120(1)(1995)215-254.

[13]Hoff D.,Strong convergence to global solutions for multidimensional flows of compressible,viscous fluids with polytropic equations fo state and discontinuous initial data.Arch. Rational Mech.Anal.,132(1995)1-14.

[14]Lions P.L.,Mathematical Topics Influid Mechanics.Vol.2.Compressible Models.New York: Oxford University Press,1998.

[15]Feiresl E.,Novotny A.,Petzeltov´a H.,On the existence of globally defined weak solutions to the Navier-Stokes equations.J.Math.Fluid Mech.,3(4)(2001)358-392.

[16]Zhang T.,Fang D.Y.,Compressible flows with a density-dependent viscosity coefficient. SIAM J.Math.Anal.,41(6)(2010)2453-2488.

[17]Huang X.D.,Li J.,Xin Z.P.,Global well-posedness of classical solutions with large oscillations and vacuum to the three-dimensional isentropic Navier-Stokes.Comm.Pure Appl. Math.,65(4)(2012)549-585.

[18]Deng X.M.,Zhang P.X.,Zhao J.N.,Global well-posedness of classical solutions with large initial data and vacuum to the Three-dimensional isentropic compressible Navier-Stokes equations.Sci.China Math.,55(2012)2457-2468.

[19]SunY.Z.,Zhang Z.F.,Ablow-up criterionofstrong solutions to the2DcompressibleNavier-Stokes equations.Sci.China Math.,54(2011)105-116.

[20]Luo Z.,Local existence of classical solutions to the two-dimensional viscous compressible flows with vacuum.Comm.Math.Sci.,10(2012)527-554.

[21]Zlotnik A.A.,Uniform estimates and stabilization of symmetric solutions of system of quaslinear equations.Diff.Equations,36(2000)701-716.

10.4208/jpde.v27.n2.5 June 2014

∗Corresponding author.Email addresses:zhpx@hqu.edu.cn(P.Zhang),dxuemei@gmail.com(X.Deng), jnzhao@xmu.edu.cn(J.Zhao)

AMS Subject Classifications:76N10,35M10

Chinese Library Classifications:O175.28,O357