The Tanh Method for Kink Solution of Some Modified Nonlinear Equation

FOROZANI Gh.and GHORVEEI NOSRAT M.

Department of Physics,Faculty of Science,Bu-Ali Sina University,Hamedan,Iran.

The Tanh Method for Kink Solution of Some Modified Nonlinear Equation

FOROZANI Gh.∗and GHORVEEI NOSRAT M.

Department of Physics,Faculty of Science,Bu-Ali Sina University,Hamedan,Iran.

Received 22 April 2013;Accepted 28 February 2014

.Thetanhmethod isaverypowerfultechnique forcomputation ofexacttraveling wave,in this paper this method has been employed for special modified states of Burger,Klein-Gordon and Fisher-Burger equations and the solitary solution of these equations are derived.

Tanh method;nonlinear equation;solitary solution.

1 Introduction

The nonlinear phenomena are very important in a variety of scientific fields,especially in fluid mechanics,solid state physics,plasma physics,plasma waves,nonlinear optics and etc[1].A variety of powerful method such as the inverse scattering[2],the Backlund transformation[3,4],sine-cos method[5],tanh-sech method[6],Hirota’s bilinear technique[7]and the homogeneous balance method[8]were used to solve nonlinear equations.The tanh method developed by Malfliet et al.[9,10],is a reliable and accurate algebraic method to obtain exact solution of nonlinear equations[11].Wazwaz also used this method for several forms of nonlinear partial differential equations such as

Fisher-Burger equation:

Klein-Gordon equation:

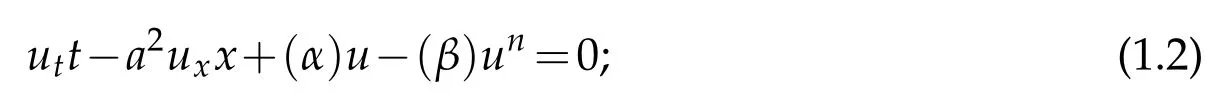
Burger equation:

Fisher-Burger equation has important applications in various fields such as traffic flow, financial mathematics,gasdynamic,appliedmathematics andphysics[12-19].Thisequationshowsaprototypicalmodelfordescribingtheinteractionbetweenthereactionmechanism,convection effect,and diffusion transport[20].In this paper solitary solution of theirs special modified states will be obtained.

2 Tanh method

Apartial differential equation(PDE)can beconvertedtoanordinarydifferential equation (ODE)upon using a wave variable[21]:

Introducing a new independentvariable y=tanhµz that leads to change of derivatives[7]:

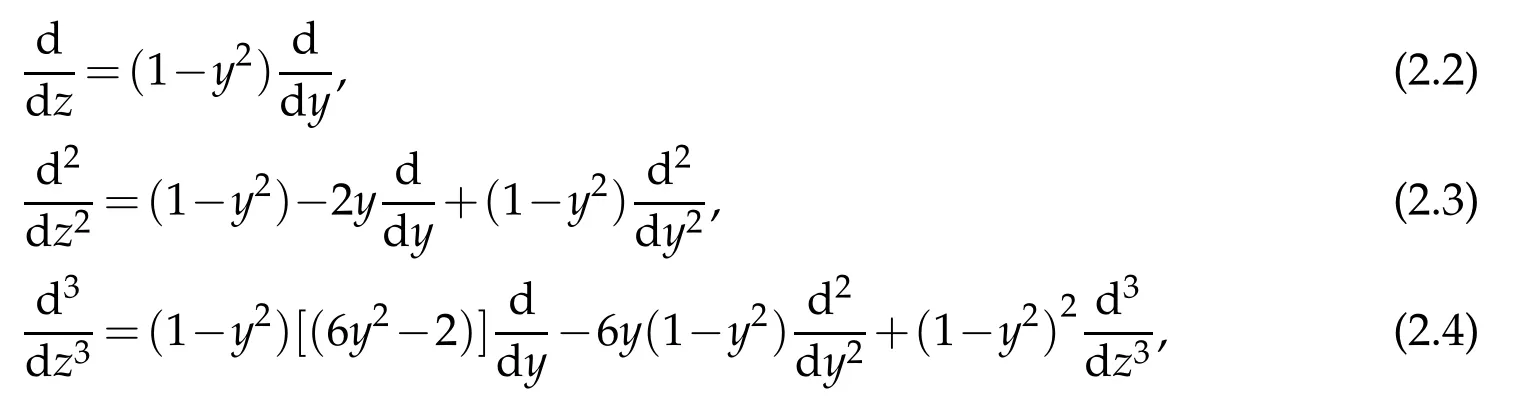
Introduce the ansatz:

where m in most cases is a positive integer.To determine the parameter m we usually balance the linear terms of highest order in the resulting equation with the highest order nonlinear terms.With m determined,equate the coefficients of powerof y in the resulting equation[1].

3 Modified nonlinear Burgers equation

By adding a nonlinear term of the form u(1-u2)to burger’s equation,the modified burger equation is obtained as follows:

Substituting(2.1)into(3.1)gives:

The m value is determined by balancing u3with u′′it is easily to shown that m is equal to 1.So that:

After substituting(3.3)into(3.2)and collecting the coefficients of each power of y,we find the system of algebraic equations for a0,a1,c andµ:

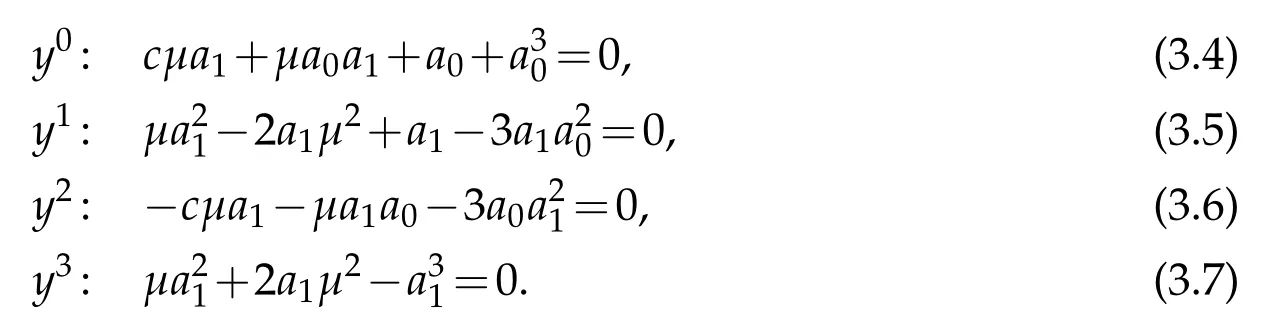
By using a simple computational program,we find:

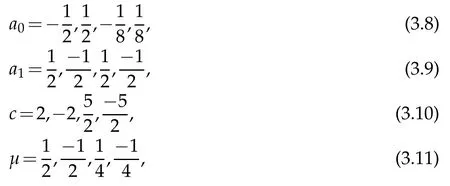
so that:

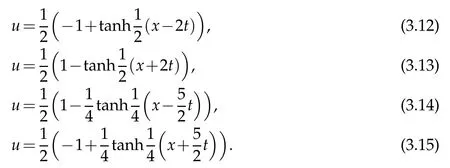
The plot of Eq.(3.5)is shown in Fig.1 and as can be seen it represent a kink.

4 Modified nonlinear Klein-Gordon equation

We now consider the modified nonlinear Klein-Gordon equation by adding a term in form uxxxto nonlinear Klein-Gordon equation:

By using wave variable(2.1)we have:

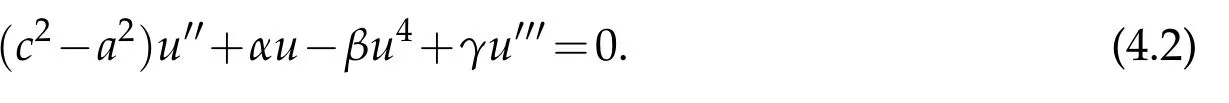
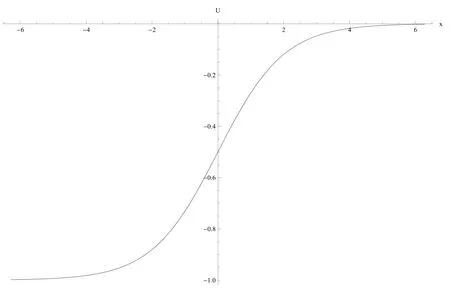
Figure 1:The plot of Eq.(3.5).

Balancing u′′with u4gives m=1 so that:

Proceeding as before we obtain the system of algebraic equations for a0,a1,µand α:

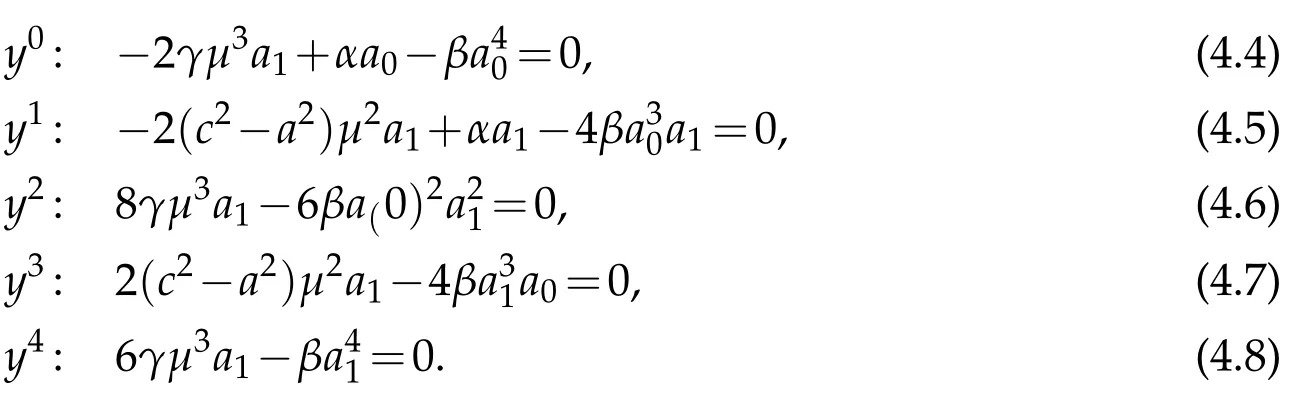
We find:

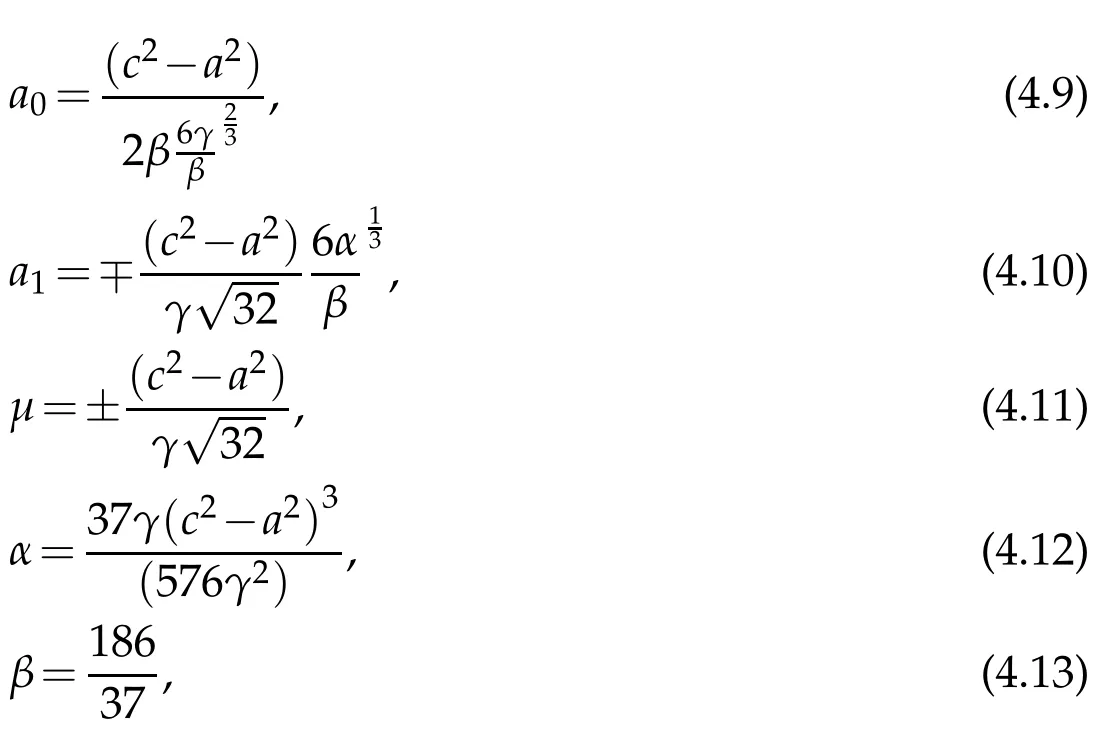
so that:

The diagram of Eq.(4.5)is shown in Fig.2 for c=2,a,α and γ=1.This diagram shown an antikink.

Figure 2:The plot of Eq.(4.5).

5 Modified nonlinear Fisher-Burgers equation

The modified Fisher-burger equation can be obtained by adding also a nonlinear term of the form αu2(1-u2)as follows:

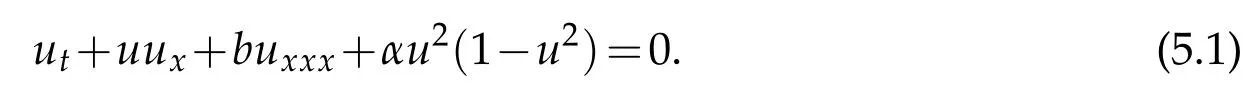
Substituting(2.1)into(5.1)gives ODE:

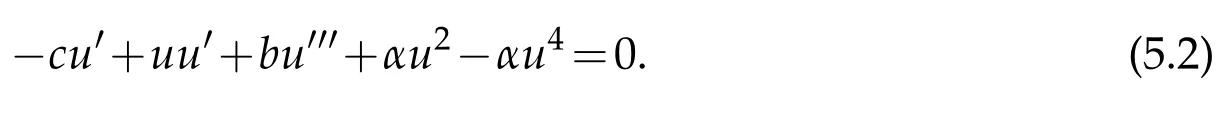
Balancing u′′whit u4gives m=1 so that:

Proceeding as before we obtain the system of algebraic equations for a0,a1andµ:With value ofwe find:

We find:

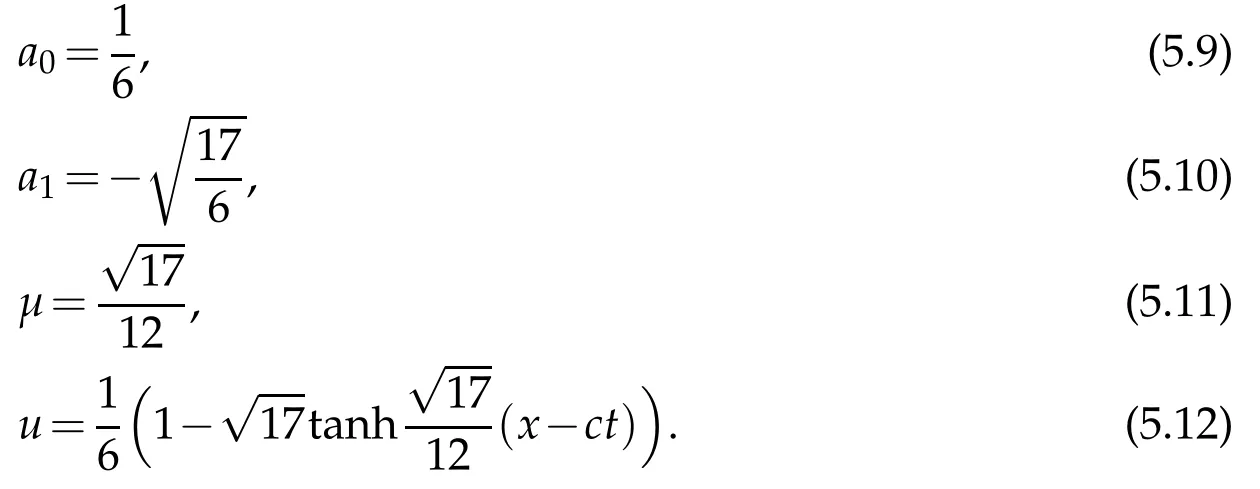
The diagram of Eq.(5.9)is shown in Fig.3.This diagram shown an antikink.

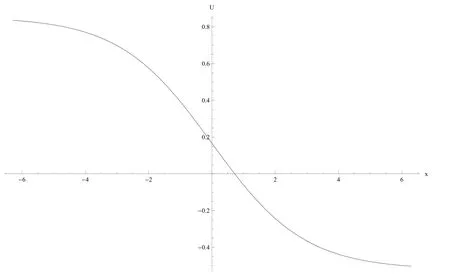
Figure 3:The plot of Eq.(5.9).

6 Discussion

The obtained results clearly demonstrate that the tanh technique is a powerful solution method to find analytical expressions for variety nonlinear equations.

References

[1]Wazwaz M.,The tanh method for traveling wave solutions of nonlinear equation.Appl. Math.Comput.,154(2004)713-723.

[2]GardnerC.S.,GreenJ.M.,KruskalM.D.andMiuraR.M.,Methodforsolving theKortewegdeVries equation.Phys.Rev.Lett.,19(1967)1095-1097.

[3]Coely A.,et al.(Eds),Backlund and Darboux Transformations,American Mathematical Society,Providence,Rhode island,2001.

[4]Ablowitz M.J.,Clarkson P.A.,Solitons,Nonlinear Evolution Equations and Inverse Scattering,Cambridge University Press,Cambridge,1991.

[5]Zhang H.Q.,Yan Z.Y.,Auto-Darboux transformation and exact solutions of the Brusselator reaction diffusion model.Appl.Math.Mech.,22(2000)541-546.

[6]Wazwaz A.M.,The tanh method for compact and noncompact solutions for variants of the KdV-Burger and the K(n,n)-Burger equations.Physica D:Nonl.Phen.,213(2)(2006)147-151.

[7]Hirota R.,Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons.Phys.Rev.Lett.,27(1971)1192-1194.

[8]Wang M.L.,Exact solution for a compound Kdv-Burgers equation.Phys.Lett.,A 213(1996) 279-287.

[9]Malfliet W.,Solitary wave solutions of nonlinear wave equations.Am.J.Phys.,60(7)(1992) 650-654.

[10]Malfliet W.,Herman W.,The tanh method:perturbation technique for conservative systems. Phys.Scr.,54(1996)569-575.

[11]Lai S.,Zheng Y.,A study of three types of nonlinear Klein-Gordon equations.Appl.Algor., 16(2009)271-279.

[12]Wazwaz A.M.,Compactons,solitons and periodic solutions for some forms of nonlinear Klein-Gordon equations.Chaos,Solit.Fract.,28(2006)1005-1013.

[13]Ismail H.N.A.,Raslan K.,Rabboh A.A.A.,Adomian decomposition method for Burger’s-Huxley and Burger’s-Fisher equations.Appl.Math.Comput.,159(1)(2004)291-301.

[14]Javidi M.,Modified pseudospectral method for generalized Burger’s-Fisher equation.Inter. Math.Forum.,1(32)(2006)1555-1564.

[15]Kaya D.,El-Sayed S.M.,A numerical simulation and explicit solutions of the generalized Burgers-Fisher equation.Appl.Math.Comput.,152(2)(2003)403-413.

[16]ChandrasekaranP.,Ramasami E.K.,Painleve analysis of a class of nonlinear diffusion equations.J.Appl.Math.Stoch.Anal.,9(1)(1996)77-86.

[17]Chen H.,Zhang H.,New multiple soliton solutions to the general Burgers-Fisher equation and the Kuramoto-Sivashinsky.Chaos,Solit.Fract.,19(1)(2004)71-76.

[18]Fahmy E.S.,Travelling wave solutions for some time-delayed equations through factorizations.Chaos,Solit.Fract.,38(4)(2008)1209-1216.

[19]Lu J.,Cui G.Y.,Jiang X.S.,Some new exact solutions to the Burger-Fisher equation and generalized Burgers-Fisher equation.Chinese Phys.,16(2007)1009-1963.

[20]Wang X.,Lu Y.,Exact solutions of the extended Burger-Fisher equation.Chinese Phys.Lett.,7 (4)(1990)145-147.

[21]Bekir A.,Cevikel A.C.,The tanh-coth method combined with the Riccati equation for solving nonlinear coupled equation in mathematical physics.J.King Saud University,23(2010) 127-132.

10.4208/jpde.v27.n2.4 June 2014

∗Correspondingauthor.Emailaddresses:g.forozani@gmail.com(Gh.Forozani),m.ghorveei@yahoo.com(M. Ghorveei Nosrat)

AMS Subject Classifications:76B25,37K40,34A34,34G20

Chinese Library Classifications:O175.14