基于复合控制的变频调速系统实验平台

孙铁成，鞠雪强，王 钰，娜仁图亚

（哈尔滨工业大学 电气工程系，黑龙江 哈尔滨 150001）

矢量控制技术，经过复杂的坐标变换，可以将电机的转矩与磁链控制解耦，达到与直流电机调速系统相媲美的调速性能［1－2］。但是矢量控制计算复杂，调速性能还受到转子参数的影响，而且对外界抗干扰能力比较弱。直接转矩控制（direct torque control，DTC）这一高性能控制策略便由此发展起来，并被推广到弱磁调速［3］。该控制方法通过Bang－Bang控制，不依赖电机数学模型的简化，不需要复杂的旋转坐标变换，结构简单，具有较强的鲁棒性［4－7］，且运行性能不受转子参数变化的影响［8］。但是直接转矩控制技术还存在以下问题［9－11］：直接转矩控制在采用 Bang－Bang控制时，会使得转矩产生较大的脉动；滞环的存在，使得系统的开关频率不能固定；低速运行时，定子电阻的压降不可忽略，定子电阻的变化会对此联模型的估算精度产生较大影响。针对直接转矩控制系统存在的问题，文献［12－13］提出了多种解决方案，使得DTC方法的调速性能有了较大的改善。

本文从DTC技术存在的问题出发，对调速系统的控制策略进行优化，提出了一种基于SVM－DTC的控制策略，并设计了一个交流调速实验平台。该实验平台面向学生设计，硬件电路主要由交－直－交变频主电路构成，其中逆变电路部分采用智能功率模块IPM，软件主要靠VC＋＋6.0对整个系统控制策略进行编程，并生成一个人机交互界面，软硬件之间通过基于PCI总线的DSP运动控制卡实现数据传输，实现实验平台的实时性和开放性控制。

1 SVM－DTC控制建模与原理

1.1 感应电机的数学模型

1.1.1 定子磁链模型

定子磁链模型的建立主要靠磁链观测器实现。本文采用鲁棒性强、结构简单易于实现的u－i模型对定子磁链Ψ进行观测，得到如下数学方程：

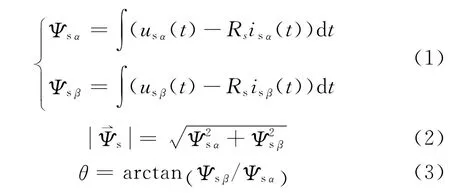
式中θ为磁链位置角。

将（1）式的方程进行组合，可得到定子磁链的u－i模型结构如图1所示。

图1 定子磁链的u－i模型结构图

1.1.2 电磁转矩模型

转矩的观测是在定子磁链观测的基础上获得的。经过坐标变换，电磁转矩Te方程为

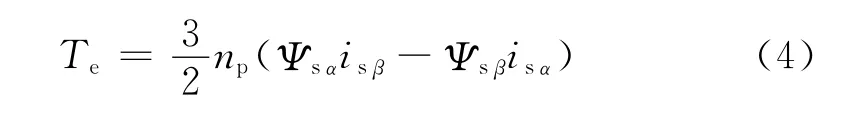
同样，经过转换之后可以得到转矩模型的结构如图2所示。图2中np为电机极对数。

图2 电磁转矩观测模型结构图

1.2 SVM－DTC的原理

如图3所示：霍尔传感器检测电机的电流信号，经过采样并转换成数字信号，由此估算出定子磁链、磁链位置角和电磁转矩的大小。经过磁链PI调节器和转矩PI调节的闭环调节，得到参考电压矢量在定子磁链x－y坐标系中的2个分量Ux和Uy，经过Park逆变换，将Ux和Uy转化为两相静止坐标系中的电压分量，将两电压分量和磁链位置角进行矢量合成便可以得到目标参考电压矢量，并判断此时目标参考电压矢量所在的扇区，计算出各扇区相应矢量的作用时间，由此产生PWM开关信号，实现系统的变频调速。

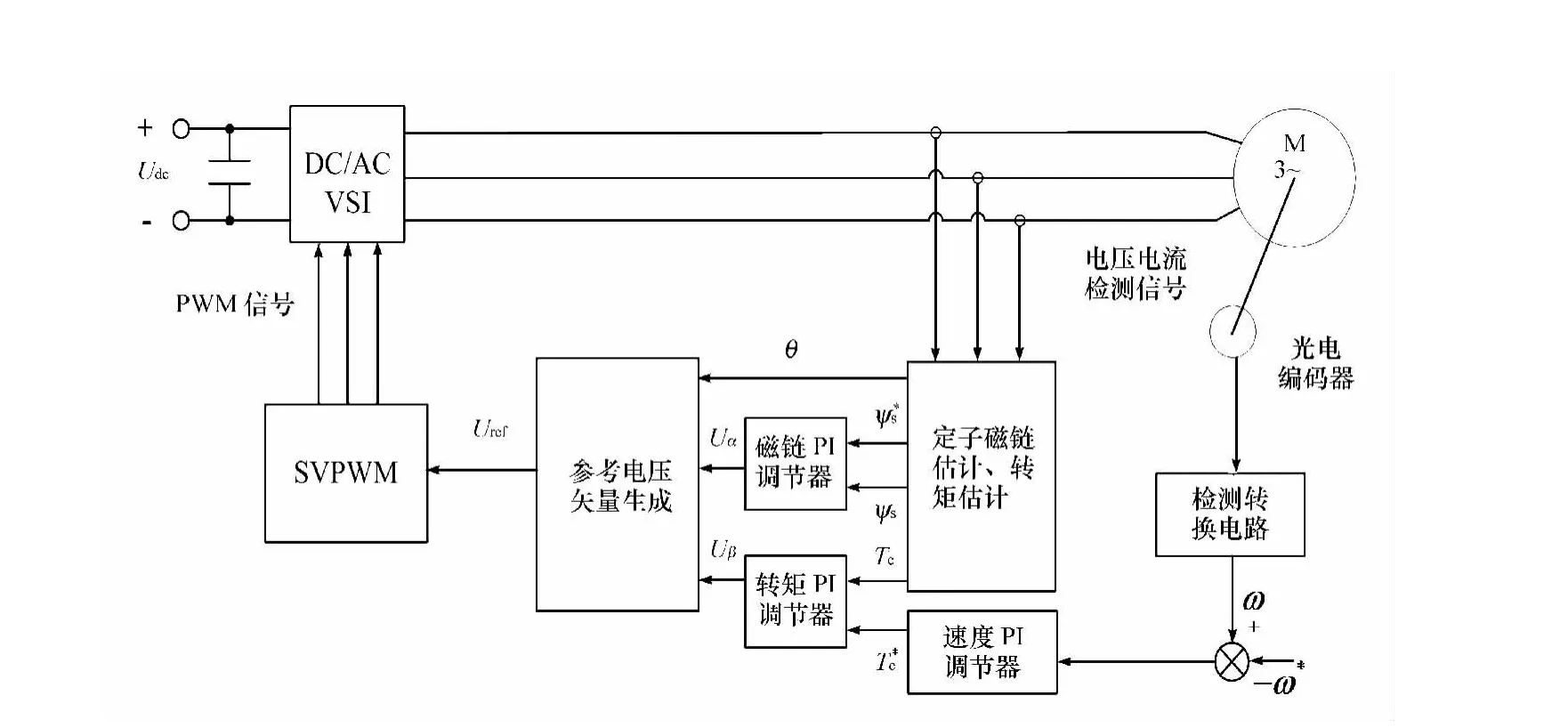
图3 SVM－DTC变频调速原理

2 SVM－DTC控制策略的实现

2.1 目标矢量所在扇区的判断

设目标电压矢量Uref在两相静止坐标系下的电压分量为Uα、Uβ，设A0、A2、A4满足下式：

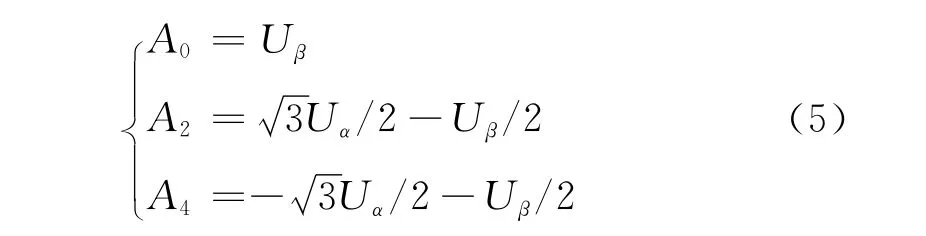
将公式（5）中求得的 A0、A2、A4的值代入下式计算P（中间变量）值，然后根据计算得到的P值查表1获得目标电压矢量所在扇区号。

表1 各P值对应的扇区号

2.2 各扇区相应矢量的作用时间确定

空间矢量调制（SVPWM）是根据目标电压矢量所在位置，选择与其相邻的基本电压空间矢量，设定这两个矢量的作用时间，然后计算并生成功率管的开关信号，从而合成目标电压矢量。如图4所示，当目标电压矢量Uref位于基本电压矢量所划分出的第Ⅰ扇区时，选择U4和U6分别作用T4和T6时间，以合成Uref。其中Ts为采样周期。

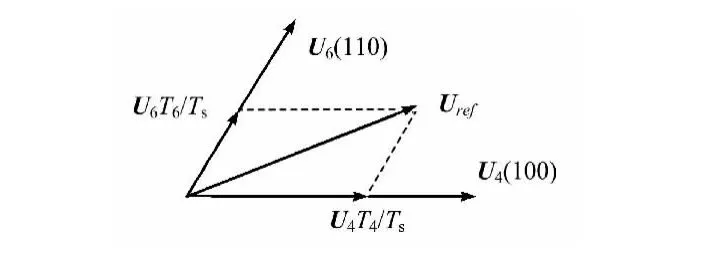
图4 目标电压矢量合成原理

设变频主电路直流母线电压为Udc，根据伏秒平衡原理，可以通过公式（7）计算电压U4、U6和零电压矢量的作用时间T4、T6、T0：

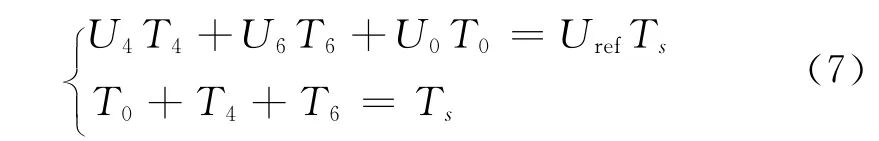
在α－β坐标系下描述为

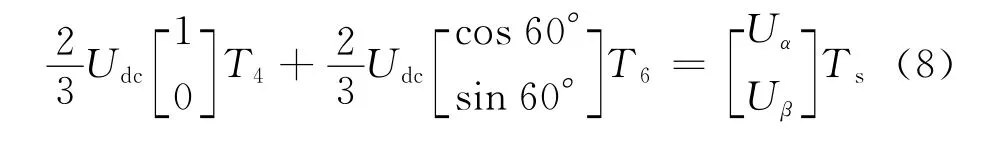
联立公式（7）和（8），可以得出电压U4和U6以及零矢量的作用时间分别为：

据此，可以很容易地计算得到各基本电压矢量的作用时间，故可以利用DSP的时间寄存器数字化实现目标电压矢量的SVPWM合成。

2.3 矢量切换点的计算

设Tcm1、Tcm2、Tcm3分别为与三角波比较生成PWM波形的3个比较值，即对应开关管的开通时刻。令Ta＝ （Ts－Tx－Ty）／2，Tb＝Ta＋Tx，Tc＝Tb＋Ty，则在不同扇区内Tcm1、Tcm2、Tcm3值得大小可以根据表2进行赋值。

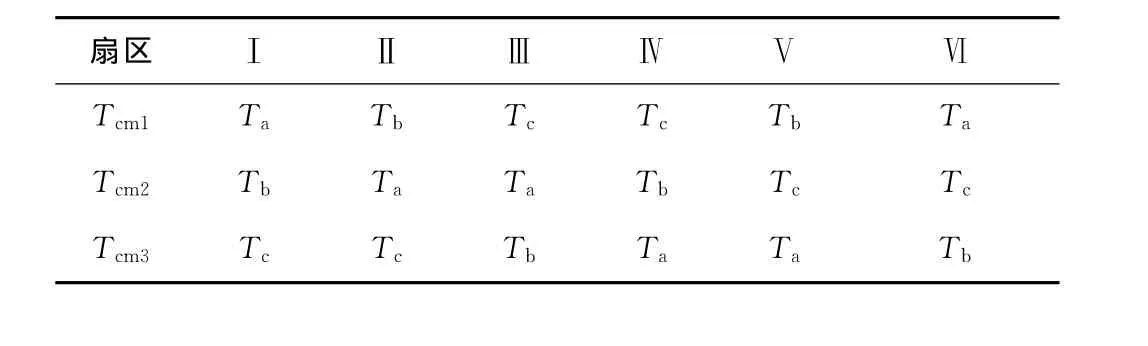
表2 扇区矢量切换点Tcm1、Tcm2、Tcm3

3 硬件电路实现

3.1 交流调速实验平台

该平台的硬件电路如图5所示，由二极管整流电路、智能功率模块逆变电路、电流霍尔传感器检测电路、DSP运动控制卡、电压检测电路、光电编码器转速检测电路，以及过压、过流保护电路和PWM信号隔离电路等组成。

图5 交流变频调速系统硬件结构图

三相交流电经过自主设计的整流电路后，经过智能功率模块IPM进行逆变，实现对感应电机的变压和变频控制。电路中的霍尔传感器、光电码盘等采集的电流、转速、电压信号输入DSP，经过DSP的A／D转换，由PCI总线传送给PC进行控制，从而产生IPM所需的PWM信号，经过光耦隔离后，由施密特反相器进行PWM信号的整形，输入IPM进行逆变。系统中的过电压、过电流保护电路可以在故障出现时关断IPM。

3.2 基于PCI总线的DSP运动控制卡

基于PCI总线的DSP运动控制卡如图6所示，上位机将控制命令和数据通过PCI发送到双端口RAM，并发出中断信号给DSP的中断引脚XINT1，DSP响应中断，去读取双端口RAM中的信息以控制电机的运行；同样，DSP将采集到的电压、电流等信号发送到双端口RAM，并发出中断信号给PCI的中断引脚LINT1，由上位机读取后进行分析和处理，并将相关参数实时显示在控制界面上。

由于PCI输出的高电平在＋2.8V和＋5V之间，而且双端口RAM的数据信号电平为＋5V，而DSP能接受的最高电平为＋3.3V，为了保证DSP及其外围器件工作的安全可靠，这就存在一个DSP与双端口RAM之间的电平转换关系问题，因此需要加总线电平转换电路。

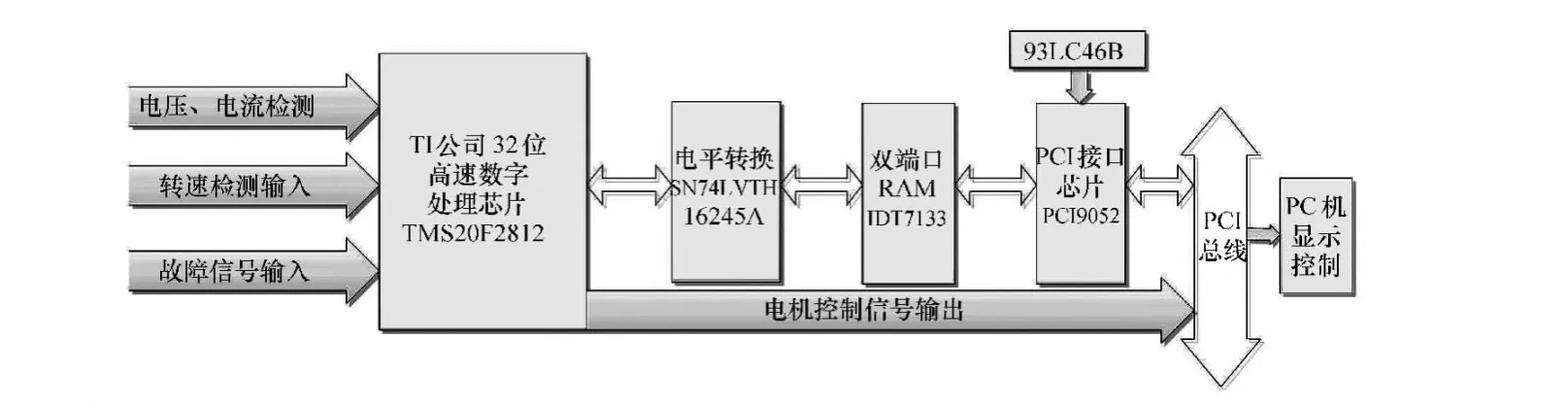
图6 基于PCI总线的运动控制卡结构图

4 人机交互界面设计

使用VC＋＋6.0进行人机交互界面窗口的设计，并对电机控制算法进行编程，本文控制策略的算法就是在此界面下进行编辑的。

图7所示人机交互界面，分为控制算法选择、在线参数修改和波形显示部分。用户可以在此界面中选择不同的电机控制算法，由不同的按钮来控制电机的启停和正反转运行，并将实验过程中采集到的实时波形与设定值进行比较输出。该界面还可以对程序算法进行在线修改，通过PCI总线与DSP进行通信，具有较强的可读性。考虑到面向学生实验，本软件具有较强的安全性和可靠性。

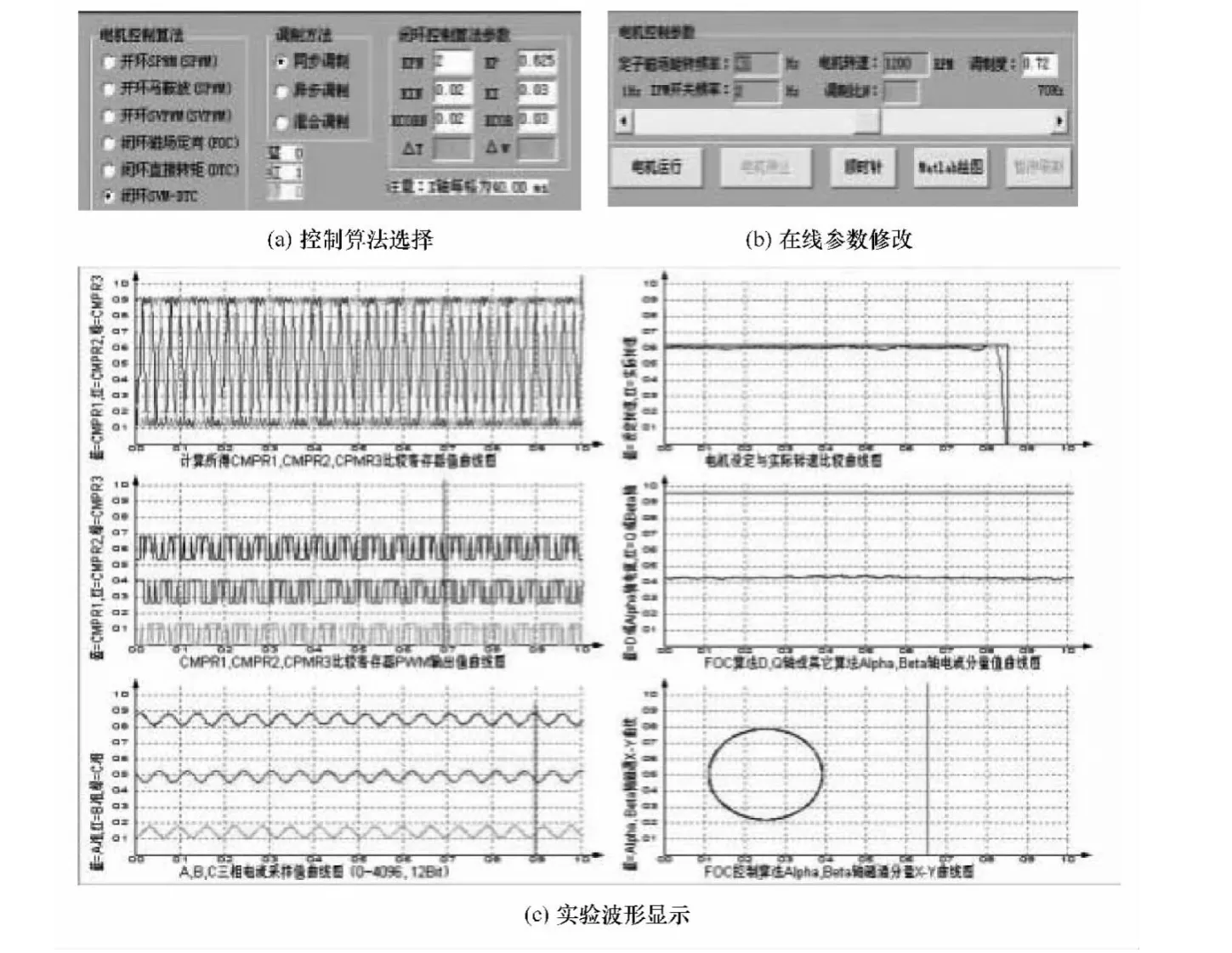
图7 人机交互软件界面

5 实验测试与结果

根据SVM－DTC控制策略的原理，在图5所示的硬件电路上进行电机动静态性能测试。实验室所用电机是三相鼠笼式异步电机，其参数如下：额定电压UN＝220V，额定功率PN＝100W，额定电流IN＝0.48A，额定频率fN＝50Hz，额定转速nN＝1 500 r／min，极对数np＝2。

5.1 静态性能测试

电机在稳定负载条件下运行时，其静态测试结果如图8—图10所示：其中图8显示的三相电流采样波形是以C相电流为基值，A、B两相电流在C相电流基础上都加了一定的数值，便于三相电流的分离显示；图9是电机在稳定负载情况下的转速变化曲线；图10是电机的磁链图。

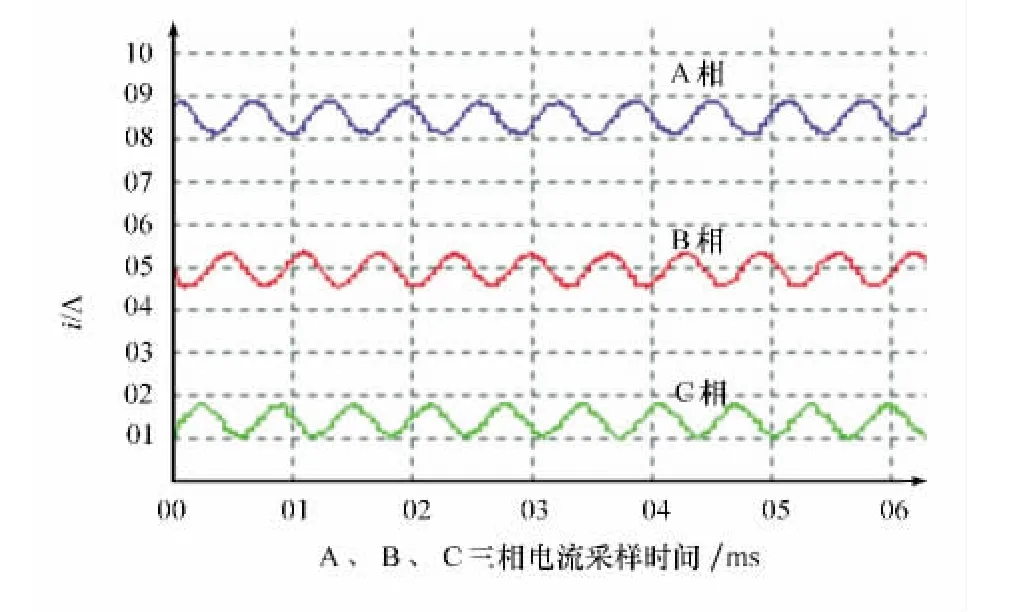
图8 三相电流波形

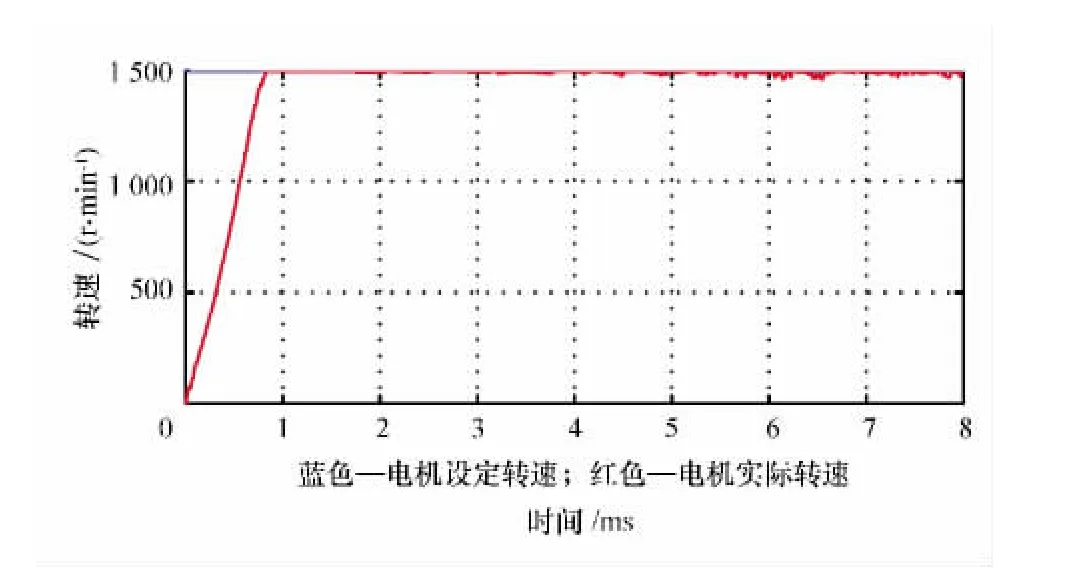
图9 电机运行速度曲线

通过实验结果可以得出：基于空间矢量调制的直接转矩控制策略下的变频调速系统，三相电流为标准的正弦波，谐波含量少；转速运行平稳，无波动；磁链基本上接近圆，静态性能较好。

5.2 动态性能测试

本文针对电机动态特性的测试主要包括：空载起动实验和动态调速实验。空载起动特性实验是在给定频率为50Hz情况下进行的，实验结果如图11所示。动态调速实验，运行频率由50Hz降到40Hz过程中，转速与电流波形变化如图12和图13所示。

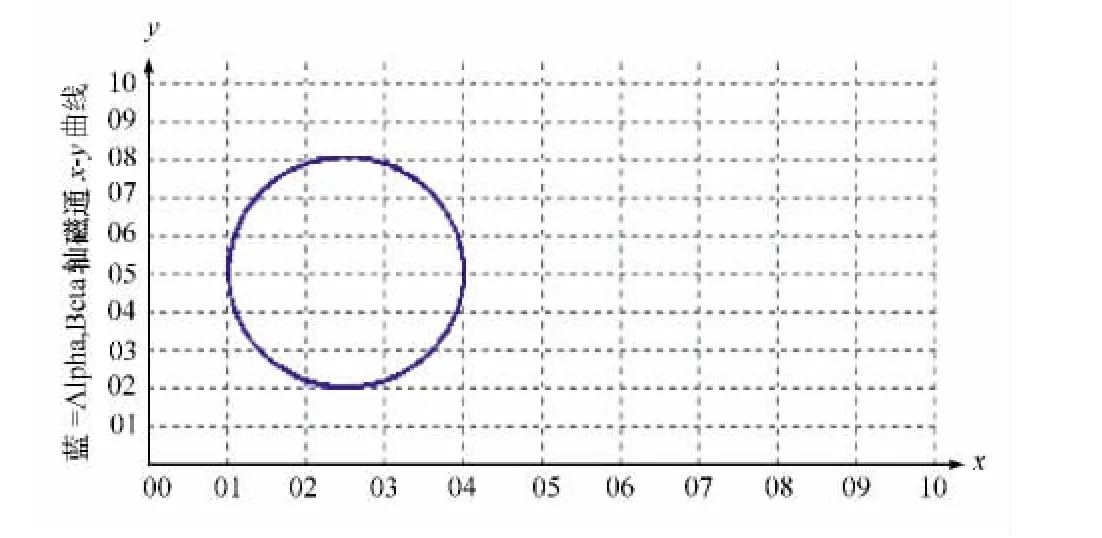
图10 电机运行过程中磁链图

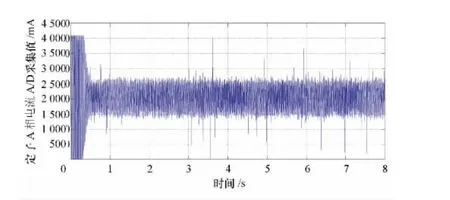
图11 空载起动时定子电流波形

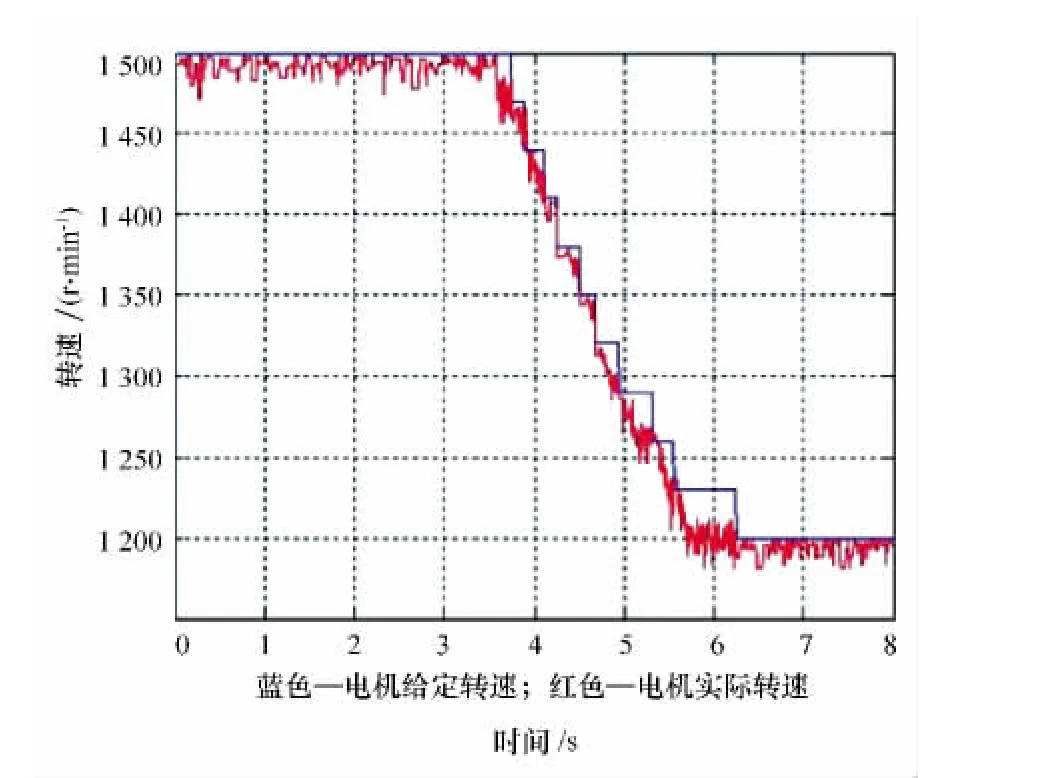
图12 电机减速的转速波形

图13 电机减速的电流波形

电机起动实验结果表明：定子电流在0.2s时间内达到稳定。电机起动后，电流响应速度快，脉动小，稳定性高，动态性能好。

变频调速实验结果表明；当电机运行过程中频率从50Hz变化到40Hz进行动态调速时，实际转速会快速地跟随给定转速变化，最后稳定在1 200r／min，电流波形会跟随转速变化而稍有波动。整个变频调速过程，响应迅速，跟随性好，具有较好的动态性能。

6 结束语

本文对基于SVM－DTC控制策略的变频调速实验进行了研究测试，有效地解决了矢量控制受参数影响，以及传统的直接转矩控制存在的低速运行时转矩和电流脉动大、开关频率不固定、定子电阻变化和磁链估算影响控制精度等问题。实验中分别进行了动静态实验和变频调速实验测试，测试结果验证了该控制策略具有较好的动静态性能，静态稳定性能高，动态响应快。

（

）

［1］唐雪峰.直接矢量控制变频调速系统研究与开发［D］.南京：南京邮电大学，2012：6－11.

［2］徐艳平，钟彦儒，杨惠.永磁同步电机矢量控制和直接转矩控制的研究［J］.电力电子技术，2008，42（1）：60－62.

［3］Emre Ozkop.Direct Torque Control of Induction Motor Using Space Vector Modulation（SVM－DTC）［C］／／Power System Conference.2008：368－372.

［4］Escalante M F，Vannier J C，Arzande A.Flying capacitor multilevel inverters and DTC motor drive applications［J］.IEEE Transactions on Industrial Electronics，2002，49（4）：803－809.

［5］Ahammad T，Bei A R，Al－Hosani K.An Improved Direct Torque Control of Induction Motor with Modified Sliding Mode Control Approach ［J］.IEEE Electric Machines ＆ Drives Conference，2013，46（13）：166－171.

［6］阮毅，陈伯时.电力拖动自动控制系统：运动控制系统［M］.北京：机械工业出版社，2010：214－216.

［7］杨建飞.永磁同步电机直接转矩控制系统若干关键问题研究［D］.南京：南京航空航天大学，2011：5－7.

［8］Aguirre M，Calleja C，Lopez－de－Heredia A，et al.FOC and DTC comparison in PMSM for railway traction application［C］／／Power Electronics and Applications（EPE 2011）.Proceedings of the 2011－14th European Conference on，2011：1－10.

［9］Busca C，Stan A，Stanciu T，et al.Control of Permanent Magnet Synchronous Generator for large wind turbines［C］／／Industrial E－lectronics（ISIE）.2010IEEE International Symposium on，2010：3871－3876.

［10］王湘明，赵旭东，董磊书.基于SVPWM的异步风力发电机直接转矩控制方法的研究［J］.可再生能源，2012，30（2）：18－22.

［11］吴桂贤.基于SVPWM的异步电机直接转矩控制研究［D］.武汉：华中科技大学，2009：3－4.

［12］严殊，肖建.一种无差拍直接转矩控制方法［J］.电机与控制学报，2007，11（2）：125－129.

［13］Lascu C，Boldea I，Blaabjerg F.A modified direct torque control for induction motor sensorless drive［J］.IEEE Trans on Industry Applications，2000，36（1）：122－130.