光干涉法测量Fe－Ni因瓦合金热膨胀系数

邓 文，徐守磊，王 昊，朱彦彦，张文春，黄宇阳

（广西大学 物理科学与工程技术学院，广西 南宁 530004）

Ni含量在35%（原子百分比）附近时二元Fe－Ni合金热膨胀系数几乎为零，具有这种特性的合金称为因瓦合金。Fe65Ni35合金在室温至100℃温度范围内，其热膨胀系数小于1.5×10－6／℃［1］。Fe－Ni因瓦合金的这种特性，能够保持零件尺寸的稳定，可用来制造精密仪器、标准量具、谐振腔、波导管、可变电容叶片、硬盘驱动器等器件，在现代工业的许多领域有广泛的应用［2－5］。因瓦效应的机理仍然是材料物理学尚待解决的难题［6－8］。由于Fe－Ni因瓦合金的热膨胀系数很小，且随温度变化的伸缩量极小。准确地测量因瓦合金的热膨胀系数是该研究的关键问题之一，对探索合金的因瓦效应机理、研发性能优良的因瓦合金十分重要［9－10］。

光干涉法测量微小位移是常用方法之一。迈克耳孙干涉仪是根据光的干涉原理制成的精密测量仪器［11－14］。本文用改装后的迈克耳孙干涉仪测量Fe－Ni因瓦合金的热膨胀系数。

1 样品制备

将纯度为99.999%的金属Fe与纯度为99.99%的金属Ni，按表1所示的化学成分配制成二元Fe－Ni合金，用真空非自耗电弧炉、在氩气保护下进行熔炼。为使成分尽可能均匀，每种合金反复熔化3次以上得到铸锭。在熔化过程中，材料损失的质量分数低于0.01%。这些铸锭在真空炉中作温度为1 000℃、时间为10h的均匀化热处理；用线切割机将铸锭切成直径为6mm、长为20mm的圆柱体，并将圆柱体的上下两切面用金相砂纸磨平、抛光后得到实验样品。

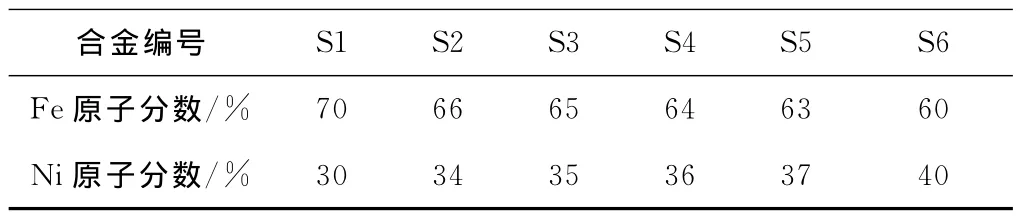
表1 Fe－Ni合金样品的化学成分

2 迈克耳孙干涉仪测量微小位移的方法

迈克耳孙光路原理如图1所示［11］，实验采用He－Ne激光器为光源，M1、M2是两块互相垂直的平面反射镜，放置在相互垂直的两臂上，M2是固定的，M1在精密螺纹杆控制下可沿滑道移动，移动的距离可以由刻度盘读出。G1是一边镀有半反半透银膜的平行平面玻璃板（称为分划板），与两轴成45°角，镀膜的作用是将入射光线分成振幅接近相等的反射光①和透射光②。G2是厚度和折射率均与G1相同的没有镀膜的平行平面玻璃板，与G1平行放置，用来补偿光线①与光线②因穿越G1次数不同而产生的光程差，G2称为补偿板。由于光束①和光束②满足光的相干条件，在光屏上相遇就形成干涉条纹［15］。M′2是 M2被G1反射所成的虚像，光束①和光束②之间的干涉等效于M1、M′2之间空气膜的干涉，M1与M′2间的空气层厚度记为d。

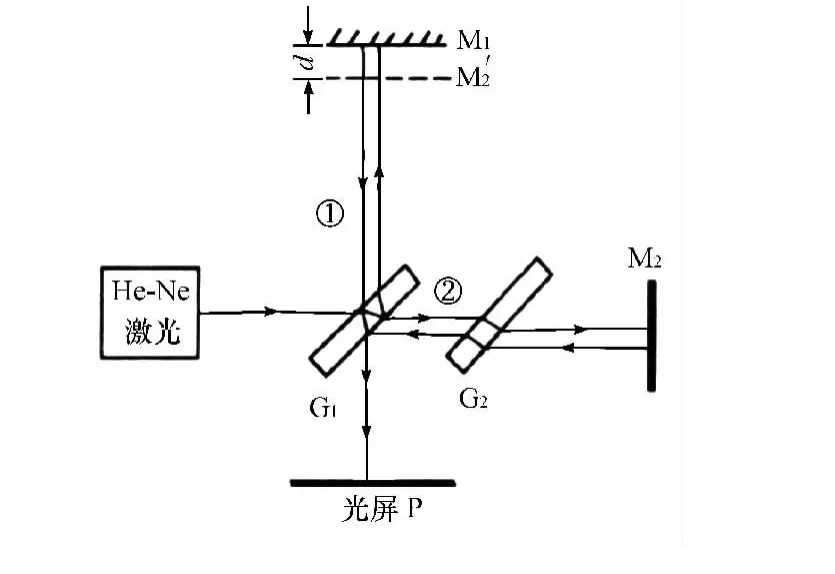
图1 迈克耳孙干涉仪原理图

在光源与G1之间加一扩束镜（图1中未给出），以提供不同角度的入射光。当 M1∥M′2（M1⊥M2）、且平行入射光时，光束1′和2′（见图2）的光程差Δ为

形成等倾干涉。形成亮条纹的条件为

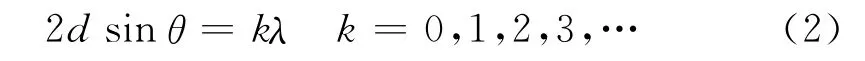
当d逐渐增大时，对任一级干涉条纹，例如k级，必定是以减少sinθ的值来满足式（2）的，故该干涉条纹间距向θ变小的方向移动，即向外扩展。这时，观察者将看到条纹好像从中心向外“冒出”。反之，当间距d由大逐渐变小时，最靠近中心的条纹将一个一个地“湮没”于中心。光程差增加或减少一个波长λ，干涉图样将从中心向外“冒出”或向中心“湮没”一个条纹，d就增加或减少λ／2，即 M1就移动了λ／2。因此，当 M1镜移动时，若有N个条纹从中心向外“冒出”或“湮没”，相当于M1移动了Δd，故有

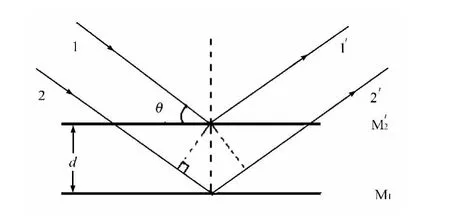
图2 等倾干涉原理图

3 膨胀系数的测量

实验时，把Fe－Ni合金加工成直径为6mm、长为20mm的圆柱体，放进内外径分别为7mm和8mm、长为18mm圆柱形陶瓷管中，圆柱形陶瓷管的外表面均匀绕上加热电阻丝，并将迈克耳孙干涉仪的反射镜M1粘在圆柱形Fe－Ni合金的垂直切面上，而圆柱形Fe－Ni合金的另一个垂直切面粘在直径约为30mm、厚度约为3mm的金属圆片中心位置处，用3颗螺丝把该金属圆片固定在支架上，再将支架紧固在迈克耳孙干涉仪的滑道上，并确保激光束始终与反射镜M1的表面垂直，靠合金的热胀冷缩来控制迈克耳孙干涉仪上全反镜M1的位置。把温度传感器粘在Fe－Ni合金上，控制加热电阻丝的电流，以改变合金的温度。

给电阻丝通上电流，圆柱形Fe－Ni合金圆柱体因被加热而膨胀，光屏上的干涉条纹不断“冒出”或“缩进”，从干涉条纹变化的数量，可以算出合金圆柱的膨胀量Δd，用数显温度计记录温度的变化Δt，根据下式计算Fe－Ni合金的线膨胀系数α［16－18］：

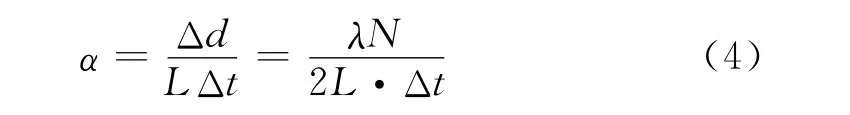
式中，L为待测合金棒原长，可由游标卡尺测得；N为当合金温度变化Δt时，干涉条纹变化的个数；λ为氦氖激光的波长（λ＝632.8nm）。

4 结果与讨论

采用改装后的迈克耳孙干涉仪，测量了不同化学成分的二元Fe－Ni合金在25～65℃的温度范围内的线膨胀系数α。Fe－Ni合金在25～65℃温区的平均热膨胀系数α随Ni含量的变化曲线见图3。

图3显示，化学成分对二元Fe－Ni合金的热膨胀系数有很大的影响，Fe65Ni35合金的热膨胀系数最小；偏离该成分，合金的热膨胀系数升高。已有的实验结果证实，当Fe－Ni二元合金中Ni含量高于35%时，合金为铁基fcc结构；当Ni含量低于20%时，合金是bcc结构；其间是两种结构的混合。铁基fcc结构是铁磁性的，因瓦效应发生在居里点以下的温度范围内［2］。一般认为，因瓦效应与产生磁有序而引起的体积效应密切相关。Weiss等［19－20］认为，Fe－Ni因瓦合金中存在2个磁有序态，一个是铁磁态（HS－high spin），一个是反铁磁态（LS－low spin），它们有着不同的平衡态体积但能量却很相近，温度升高时一些铁磁态向反铁磁态转变，由此产生大的自发体积磁致伸缩，因而抵消点阵的热膨胀。Endoh［3］以及鲜于泽［5］等人发现，在居里点以下呈现因瓦效应时，声子明显软化，因瓦效应来源于费米能级处态密度的增大。

本文结果表明，利用改装后的迈克耳孙干涉仪，可准确并快速地测量固体长度微小变化量，是测量材料热膨胀系数的有效方法。这为探索合金的因瓦效应机理、研发性能优良的因瓦合金提供了重要的实验方法。

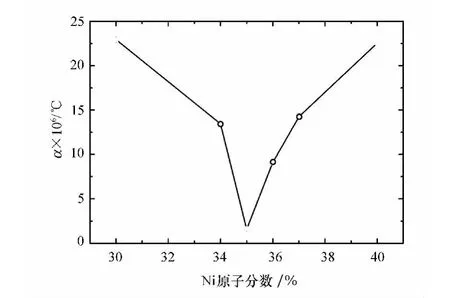
图3 Fe－Ni合金在25～65℃温区的热膨胀系数α随Ni含量的变化曲线

5 结论

（1）利用改装后的迈克耳孙干涉仪，可准确并快速地测量固体长度微小变化量，是测量材料热膨胀系数的有效方法。

（2）化学成分对二元Fe－Ni合金的热膨胀系数有很大的影响，Fe65Ni35合金的热膨胀系数最小，偏离该成分，合金的热膨胀系数升高。

（

）

［1］Masayyuki Shiga.Lattice parameter and magnetic moment in 3d transition metal alloys：The origin of invar effects ［J］.IEEE Transactions on Magnetics，1972，8（3）：851－859.

［2］Gorria P，Martinez－Blanco D，Perez M J，et al.Structure and magnetism of Fe－rich nanostructured Fe－Ni metastable solid solutions［J］.J magn magn mater，2005，294（2）：159－164.

［3］Endoh Y.Lattice dynamics in ferromagnetic invar alloys［J］.J magn magn mater，1979，10（2／3）：177－182.

［4］Ishikawa Y，Ondera S，Tajima K.Magnetic excitations in invar alloys Fe65Ni35and Fe3Pt［J］.J magn magn mater，1979，10（2／3）：183－190.

［5］鲜于泽，卢志超，李际周，等.铁基非晶态因瓦合金的声子谱研究［J］.物理学报，1994，43（1）：99－101.

［6］Schroter M，Ebert H，Akai H，et al.First－principles investigations of atomic disorder effects on magnetic and structural instabilities in transition－metal alloy［J］.Phys Rev B，1995，52（1）：188－209.

［7］Wassermann E F.Invar：moment－volume instabilities in transition metals and alloys［G］／／Buschow K H J，Wohlfarth E P ed.Ferromagnetic Materials， Vol 5， Amsterdam： North－Holland，1990：237.

［8］Gulyaev A A，Svistunova E L.Precipitation process and age－hardenability of Fe－Ni－Be invar alloys［J］.Scripta metallurgica et materiala，1995，9（33）：1497－1503.

［9］Andreev A V，De Boer F R，Jacobs T H，et al.Thermal expansion anomalies and spontaneous magnetostriction in R2Fe17Cxintermetallic compounds［J］.Physica B，1991，175（4）：361－369.

［10］Ono F，Matsushima Y，chimi Y，et al.Irradiation－induced ferromagnetism in Fe－based invar alloys with high－energy heavy ions［J］.J magn magn mater，2007，310（2）：1864－1865.

［11］程守洙，江之永.普通物理学：下册［M］.北京：高等教育出版社，2008：151－153.

［12］陈业仙，周党培，关小泉，等.一种新型迈克耳孙干涉仪条纹计数器的设计［J］.大学物理实验，2009，22（3）：64－67.

［13］张萍，侯晨霞，宋金璠.综合设计性实验教学的研究与探讨：迈克耳孙干涉仪的拓展应用［J］.实验技术与管理，2011，28（8）：157－175.

［14］肖化，漆建军.利用线阵CCD的迈克耳孙干涉仪测量压电材料的压电系数［J］.实验技术与管理，2011，28（2）：24－27.

［15］周菊林，梅孝安，李蓓.微小长度变化量的实验研究［J］.实验室研究与探索，2011，30（10）：24－27.

［16］郑文轩，吴胜举，杨瑛.用迈克耳逊干涉仪测固体线胀系数［J］.实验科学与技术，2007（6）：8－9.

［17］王昆林，朱箭，刘子臣.激光干涉法测定固体线胀系数［J］.实验科学与技术，2004（1）：14－15.

［18］郝久清，王莉.Fe78Si9B13非晶合金薄带线膨胀系数的研究［J］.科学技术与工程，2011，11（20）：4684－4686.

［19］Weiss R J.The origin of the“invar”effects［C］／／Proc R Soc London，1963：281－285.

［20］Abrikosov I A，Eriksson O，Soderlind P，et al.Theoretical aspects of the FecNi1－cInvar alloy［J］.Physical review B，1995，51（2）：1058－1063.