基于应变的X65悬空压力管道失效长度分析
朱亚明,马廷霞,张朋飞,陈红霞
西南石油大学机电工程学院 (四川 成都 610500)
中石油西部管道公司所辖管线沿线地质地貌错综复杂,如兰成渝管道,地形复杂,地震频繁,河流多,且雨季长,经常出现埋地管道在洪水冲刷下形成局部悬空。地质灾害频繁发生,给管道的悬空长度、承载能力造成一定的影响,甚至发生断裂,一旦发生危险,严重的可能造成油气泄露污染环境,甚至可能燃烧爆炸,可见压力管道的完整性直接关系到生产的安全[1-3]。X65管线钢是油气储运中主要的集输工具材料,具有良好的工艺和力学性能,管线钢的应力-应变关系呈显著非线性,因此精确描述管线钢应力应变关系是管线钢结构受力及稳定性分析等相关研究工作的基础。本文对X65管线钢的本构关系进行了研究并对其进行了修正。失效研究大多是基于应力的失效分析,研究表明在地震、滑坡、冻土等特殊工况环境下,悬空管道承受的应变和位移很大,虽已达到或超过应力判别的要求,但管道还能满足输送要求。用Abaqus软件对X65悬空压力管道进行有限元建模,对其进行基于应变的失效分析。
1 对X65管材的本构关系的研究
1.1 X65管材的本构关系
在万能材料试验机上,对X65(L450)钢材试样(10件)进行拉伸试验,得到曲线(图 1(a)),选取其中的一条典型的曲线(图1(b))。
1.2 对X65管材理论本构关系研究及其修正
采用弹塑性理论建立其本构关系。由图1可看出管线钢进入塑性后,其应力应变表现为典型的非线性。在比例变形条件下,通过对增量理论的应力和应变增量关系的积分可得到全量理论的应力—应变关系。在此以全局二段式应力—应变模型为例分析。
第一阶段为应力在条件屈服极限范围内,即ε≤εp0.2(卸载后剩余0.2%的塑性变形所对应的应变,无量纲)时,采用传统的Ramberg-Osgood本构模型来表示单轴非线性应力-应变关系;此模型视总应变ε总为弹性应变εe和塑性应变εp之和,其具体形式为:
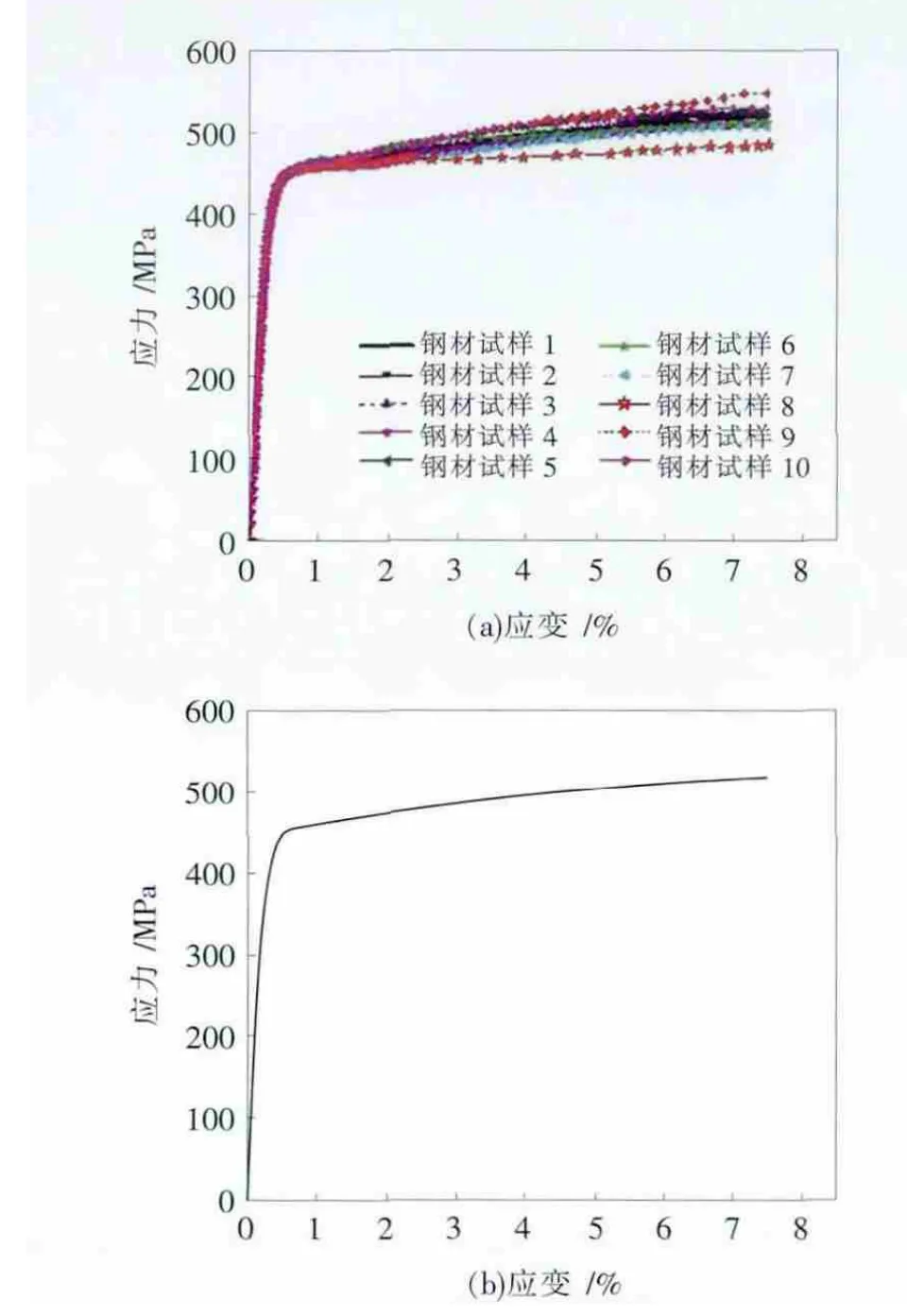
图1 X65(L450)管材的应力-应变关系曲线
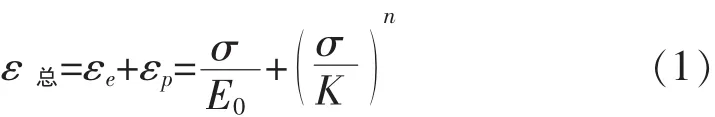
式中:σ为应力,MPa;K为应变硬化相关系数;E0为初始弹性模量,MPa;n为应变硬化指数。
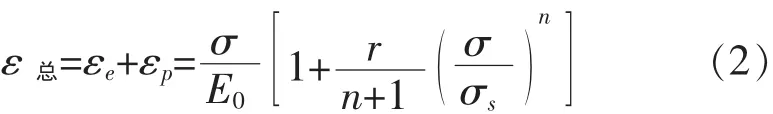
式中:σs为屈服强度,MPa;ε0为初始应变 (ε0=σs/E0);n、r为 Ramberg-Osgood 参数。
X65管材中n=8,r=14,代入(2)得到X65管材的本构关系方程:
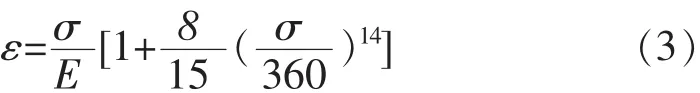
按照Ramberg-Osgood关系建立的曲线与X65管线钢实验本构关系曲线进行对比,如图2所示。
由图2知X65管材的应力—应变曲线在应变值比较低的情况下,方程(3)能够准确地反应。但当应变高于条件屈服极限时的应变εp0.2以后,上述模型所求得的数值误差较大,因此有必要对R-O模型做出修正。
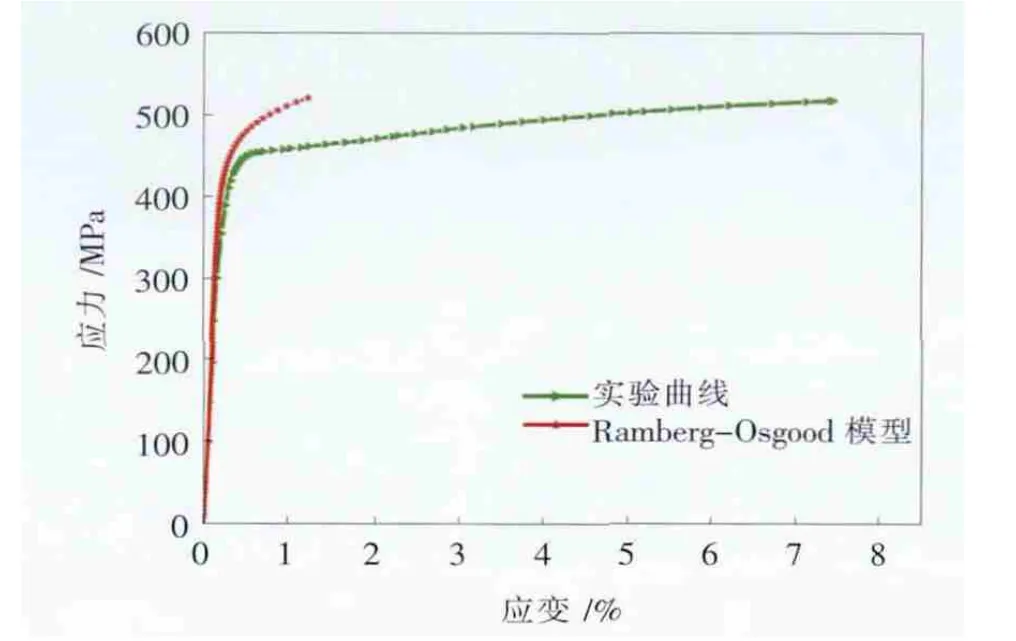
图2 X65管线钢R-O模型与实验实测值应力-应变曲线对比图
第二阶段为应变范围在εp0.2<ε时,根据实验数据,提出用条件屈服极限σp1.0来代替极限应力,在σp0.2和极限应力σp1.0间采用如下表达式[4],即:

式(4)中,E0.2为应力等于σp0.2时的切线模量;εp0.2=0.2%,εp1.0=1%,与之对应的应力分别记为σp0.2和 σp1.0,n0.2,1.0为描述 σp0.2和 σp1.0间曲线段的应变硬化指数,其值可根据模型与实验所得应力-应变曲线的符合程度求出。推导出此阶段的应力应变关系式如下:

因此X65管材的本构关系具体表示为:
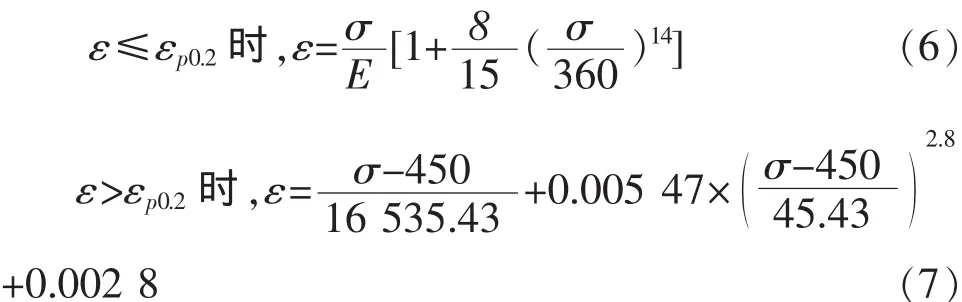
依据上述公式描述的应力-应变本构关系曲线如图3所示。
由图3,可以看到推导的公式与实验曲线很好的拟合,即修正后的X65管材的Ramberg-Osgood关系式与实验数据拟合得很好,此公式可以精确地反应X65管线钢的应力应变关系。
2 悬空管道的应变极限
我国对于建立力学模型及悬空状态下管道的基于应变失效的分析不多,但当管道遇到自然灾害时,管道应力超过比例极限后的继续变形,基于应力的设计已不再适用,此时基于应变的管道安全准则更为合理。挪威、加拿大等一些国家已经开始采用基于应变的设计准则[5]。基于应变的安全评估方法的关键,是确定管道在将要承受的应变及管道本身所能够承受的应变极限,而这个应变极限可以通过有限元分析确定。
图3 X65管线钢实验实测结果与各模型的应力-应变关系
2.1 拉应变极限
当管道存在缺陷时,拉伸应变达到或超过极限值,可能导致管道断裂。为了防止薄膜断裂,一次载荷、二次载荷或二者组合引起的拉伸应变应满足以下因子化的载荷-阻力设计公式[6]:

式(8)中:εtf为纵向或环向的因子化拉伸应变;φεt为拉伸应变的阻力因子,可取0.7;εtcrit为管道的拉伸极限应变,由实验确定,且应考虑缺陷、焊缝及热影响区等,当缺乏具体信息时拉伸极限应变取0.75%,这是保守的取值,海底管线的取值为2%[7]。
2.2 压应变极限
管线局部屈曲表现在管壁出现皱褶起纹,最终产生环管壁的裂缝。通过试验研究 ,Hall和Newmark认为管线屈曲失效时的应变值为0.15t/R~0.20t/R。R为半径 ,t为壁厚[8]。
应用基于应变的悬空管道失效判据,按拉应变极限,将 φεt=0.7,εtcrit=0.75%代入公式(8)得到 εtf≤0.525%;按压应变极限,管线屈曲失效时的应变值为0.196 7%~0.26%。而在实际操作下,只要悬空管道进入塑性变形,就会对管道进行维护和抢修。因此本文采用极限悬空长度对应的最大应变值为0.525%,安全悬空长度对应的应变值为0.2%。
3 失效分析
3.1 工况概述
采用目前国际上先进的有限元分析程序Abaqus进行计算,悬空管道的力学建模借助大挠度梁理论、弹性地基理论、管-土互作用双线性模型、Winkler弹性地基梁模型,考虑管道的几何非线性和土壤的物理非线性[9-11]。由于结构与载荷在轴向与竖直方向具有对称性,因此采用四分之一结构。对管道进行网格划分,管体采用三维4节点减缩壳单元(S4R),土体采用 8节点线性减缩积分单元(C3D8R)。管道及土体和管道接触部分网格划分比较密集,远离管道处的土体单元相对稀疏。
以X65管材为例,建立完全悬空管道的有限元计算模型,计算参数采用新疆乌鄯原油支干线段设计参数。管材塑性阶段的本构关系由修正后的X65管材的Ramberg-Osgood关系式与试验数据拟合的公式(7),代入应力值求得应变,见表1。
3.2 基于应变失效的悬空管道长度分析
本次分析分2组进行对比,2组数据都为X65管材,直径为610mm的管子,在其他工况条件都相同的状况下,第1组以管道内压为变量,管道壁厚均为8mm,分析内压为8MPa和10MPa时,在悬空长度为 50、100、150、200、300、400、520(560)、700m,时,得到应力应变关系,如图4所示。第2组以壁厚为变量,管道内压均为10MPa,分析在壁厚分别取8mm和10mm时的悬空长度与应变的关系,如图5所示。
由图4可以看到在悬空长度超过200m时,应变随着悬空长度的增加呈线性增长,应力曲线斜率逐渐趋于零,这也验证了基于应变的实效判别标准较为合理。在内压为8MPa时,悬空长度为700m时,达到管道的屈服强度520MPa;以应变失效判别时,最大安全悬空长度为250m,极限悬空长度为430m。内压为10MPa时,悬空长度为660m时,达到管道的屈服强度520MPa,以应变失效判别时,最大安全悬空长度为202m,极限悬空长度为350m。同时,由图4知,在其他条件相同的工况下,内压增大,管道应力应变值增加较快,管道的安全悬空长度和极限悬空长度将会减小。
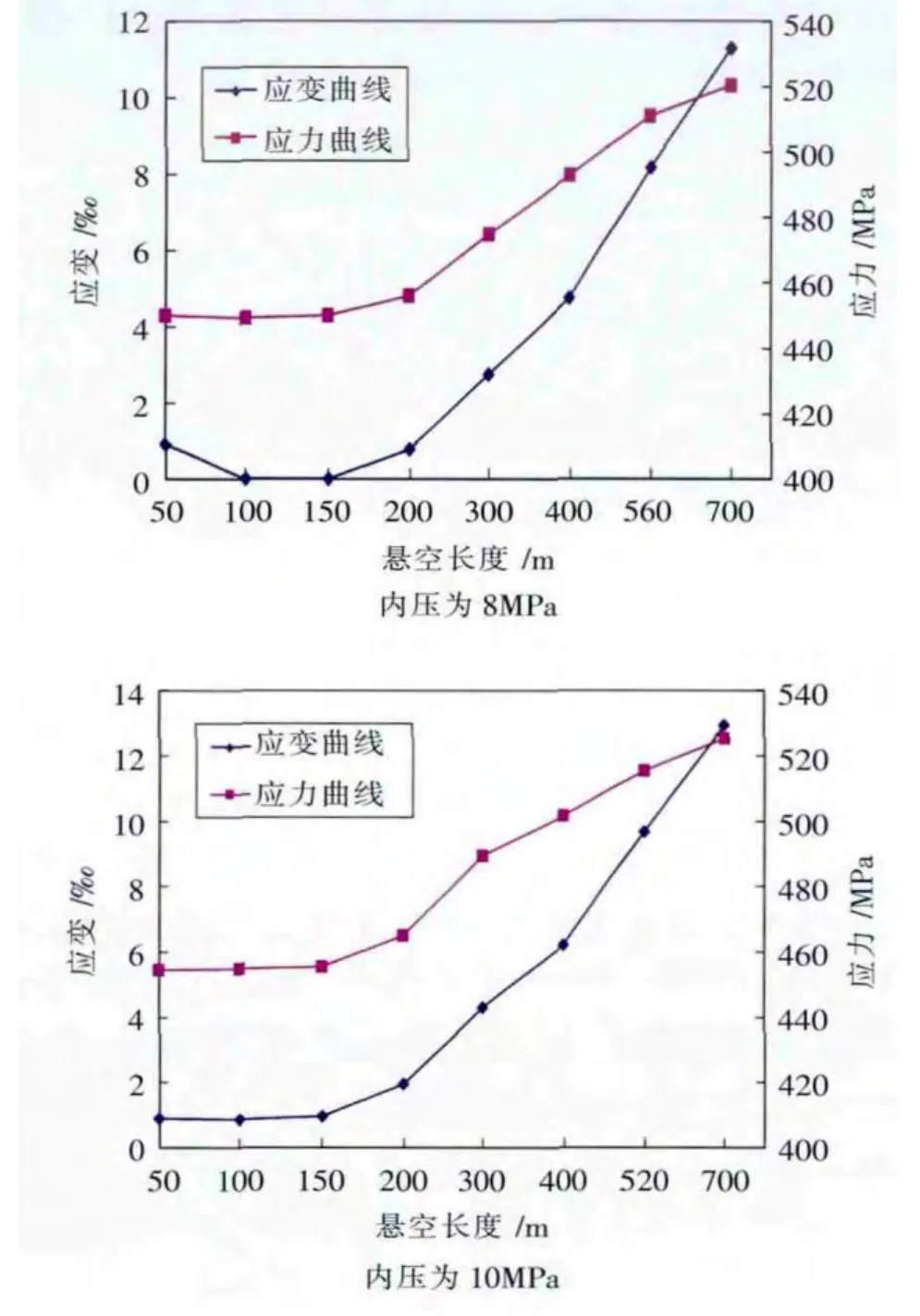
图4 内压不同时悬空长度与应力应变关系图
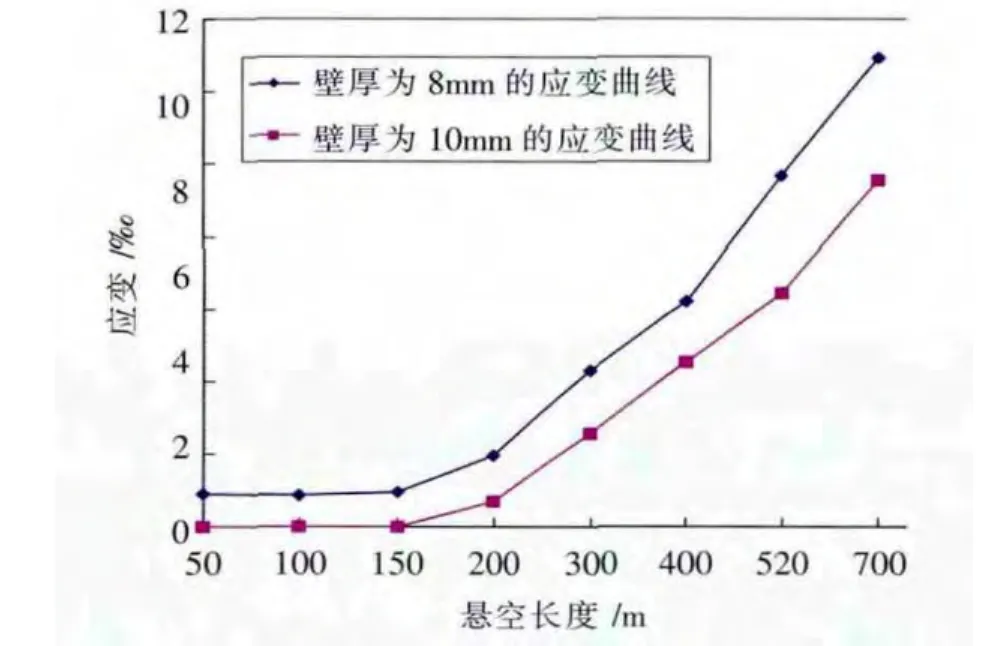
图5 壁厚不同内压相同的悬空长度与应变关系图
由图5同样可以看到应变的增长随着悬空长度的增大呈线性增长,在应变值为2.756‰~14‰间斜率增大使得应变增大更快。且在内压相同的情况下壁厚越薄,应变越大。以应变失效判别,壁厚为8mm时,最大安全悬空长度为202m,极限悬空长度为350m。壁厚为10mm时,最大安全悬空长度为270m,极限悬空长度为431m。同时,由图5在其他条件相同的工况下,壁厚减小,管道应变值增加较快,管道的安全悬空长度和极限悬空长度将会减小。
4 结论和建议
修正后的X65管材的Ramberg-Osgood关系式与实验曲线拟合的很好,通过修正后的关系式可以更准确地得到X65管材的应力应变数据。
通过悬空长度与应力应变的关系曲线,验证了基于应变失效的判别标准的合理性。
通过有限元分析,得到只有壁厚为变量时,最大安全悬空长度和极限悬空长度随着壁厚的增大而增大;只有压强为变量时,最大安全悬空长度和极限悬空长度随着压强的增大而减小。
当管道发生悬空,在安全悬空长度以内的管道可以等自然灾害过后,再进行抢修;如果超出安全悬空长度时,建议立即对管道进行抢修。
[1]王为民,张文伟.黄土地区长输管道地质灾害分析及治理[J].油气储运,2001,20(4):28-31.
[2]冯庆善,陈健峰,艾慕阳,等.管道完整性管理在应对地震灾害中的应用[J].石油学报,2010,31(1):139-143.
[3]O’Donnell H W.Investigation of flood induced pipeline failures on lower San Jacinto River[C].Proceedings of the Pipeline Division SpecialtyConference.New York,United States,ASME,2005.
[4]王孟鸿.钢结构非线性分析与动力稳定性研究[M].北京:中国建筑工业出版社,2005.
[5]刘冰,刘学杰,张宏.基于应变的管道设计准则[J].天然气工业,2008,28(2):129-131.
[6]Canadian Standards Association.CSA Z662-07,Oil and Gas Pipeline Systems[S].
[7]Det Norske Veritas(DNV).DNV-OS-F101,Submarine Pipeline Systems[S].
[8]高建,王德国,何仁洋,等.基于应变的悬空管道性能分析[J].管道技术与设备,2011(6):13-15.
[9]马廷霞,吴锦强,唐愚,等.成品油管道的极限悬空长度研究[J].西南石油大学学报:自然科学版,2012,34(4):165-173.
[10]罗金恒,赵新伟,王峰会,等.地质灾害下悬空管道的应力分析及计算[J].压力容器,2006,23(6):23-26.
[11]杨毅,闫宝东,廖柯熹.输油管道悬空管段应力计算[J].石油学报,2011,32(5):911-914.

