应用灰色模糊马尔科夫链预测海河水质变化趋势

于 慧,孙宝盛,李亚楠,张 燕,齐庚申

(天津大学环境科学与工程学院,天津 300072)

应用灰色模糊马尔科夫链预测海河水质变化趋势

于 慧,孙宝盛*,李亚楠,张 燕,齐庚申

(天津大学环境科学与工程学院,天津 300072)

灰色 GM(1,1)模型在水质预测中得到了较为广泛的运用,但其存在灰色偏差与抗干扰能力弱的局限性,针对这一问题,将马尔科夫链理论与模糊集合理论引入灰色GM(1,1)预测模型,并应用该模型对海河三岔口断面的DO、CODMn和NH3-N 3项指标2012～2016年的浓度变化趋势进行预测.结果表明,2004～2016年,DO及NH3-N浓度大致呈上升趋势,预计2016年分别可达9.15,1.47mg/L;CODMn浓度呈下降趋势,预计2016年可达3.91mg/L.以2012年的数据做验证,灰色模糊马尔科夫链模型的预测精度最高,可作为科学的水质预测方法.

GM(1,1)模型；模糊分类；马尔科夫模型

水质预测是水环境规划、评价和管理工作的基础,通过预测,可以了解当地水域环境质量演变趋势,进而及时发现水质恶化的原因并采取相应的治理措施[1-3].目前,常用的预测方法有数理统计预测法、灰色系统理论预测法、神经网络模型预测法、水质模拟模型预测法、混沌理论预测法等[4].受水文、水质监测条件的限制,水质预测过程中往往缺乏长期的水质资料,而灰色系统分析法对于信息不完整(或不完全)情况,具有良好的适用性[5-8].但灰色模型预测由于其原始数据的起伏性和无序性等,难以将预测带限制在一个较小的范围之内,导致灰色预测模型在大多数情况之下是粗糙的[9].有研究指出,可以通过对灰色预测模型的结果进行马尔科夫链改进来提高其预测的准确性[10-12].因此,本文把模糊集合理论与马尔科夫链理论引入灰色预测算法中,提出灰色模糊马尔科夫链预测方法,并用残差修正模型对计算过程进行优化.一定程度地解决了影响灰色预测精度提高的存在灰色偏差与抗干扰能力弱的问题.本文结合水质标准,应用灰色模糊马尔科夫链预测模型,对海河三岔口段的水质进行预测.

1 区域概况

海河,起自天津下西部的南运河、子牙河相交的的三岔河口西,东至大沽口入海,全长 70km,流域面积达 26.36万 km2,大陆季风性气候区,平均年降水量为548mm,海河水系上游支流繁多分散,下游集中,河道容泄能力上大下小,极易形成洪峰.海河地处津京唐工业区,重工业发达再加上地处华北的水资源紧张地区,气候干燥,降水少,蒸发量大,河流径流量小,海河是一条污染较严重的河流[13-15].海河区域概况示意见图1.

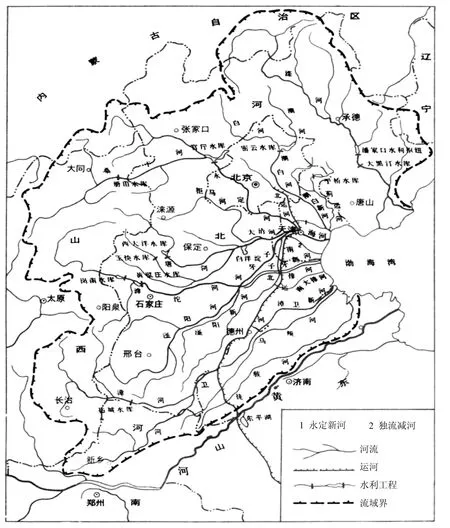
图1 海河流域区域概况示意Fig.1 Regional overview diagram

2 研究方法

2.1 GM(1,1)模型

GM(1,1)模型是最常用的灰色预测模型,它是灰色系统理论中一种动态序列处理方法,将随机量当作在一定范围变化的灰色量,随机过程当作在一定时区变化的灰色过程,并认为微分方程是背景值与各阶灰导数的某种组合.用于数列预测的 GM(1,1)模型的特点是利用单变量时间序列数据进行预测.将无规律的原始数据经生成后,使其变为较有规律的生成数列再建模,因此GM(1,1)模型实际上是生成数列模型,一般用微分方程描述.它是一个单变量预测的一阶微分方程模型,其离散时间响应函数近似呈指数规律.

本文采用2004～2012年监测周报中的数据,对每个监测断面选取溶解氧(DO)、高锰酸盐指数(CODMn) 和氨氮(NH3-N) 3个监测指标作为研究对象,进行年平均计算处理后作为实测数据进行预测.采用 2004～2011年的数据建模,使用2012年份数据验证.以预测DO的变化趋势为例,其浓度见表1.

表1 2004～2012年海河三岔口断面的溶解氧浓度(mg/L)Table 1 The concentration of DO at three fork section of Haihe River during 2004～2012(mg/L)

设原始数据序列为 X(0),则 X(0)=(χ(0)(1), χ(0)(2),…,χ(0)(n))=(9.21,8.16,8.53,9.24,8.18,7.00,8. 55,8.57,9.68)为了减弱极端值的影响,强化原始数列的大致趋势,采用滑动平均法对原始数列进行改造,记原始数列为{χ(0)(t)};t=1,2,…,n,滑动平均值计算公式如下∶

对于两端点的计算用以下公式∶

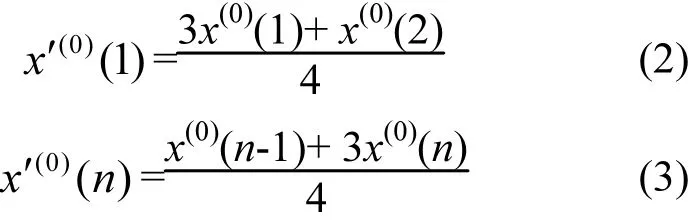
由此可得∶X′(0)= (8.95,8.52,8.62,8.80,8.15, 7.68,8.17,8.84,9.40)

2.1.1 取得累加生成数列[16]对 X′(0)做 1-AGO得累加生成数列X′(1),公式为∶

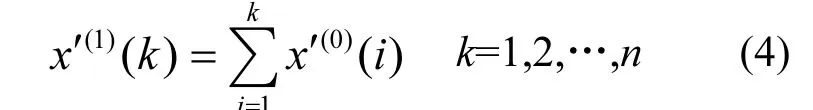
2.1.2 对X′(0)进行光滑性检验 准光滑性检验公式为∶

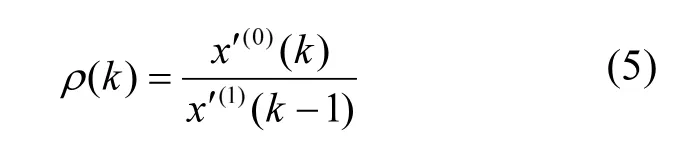
当ρ(k) <0.5时满足光滑条件,其值见表2.

表2 准光滑性检验Table 2 Quasi smoothness test

由表2可以看出,当k>2后满足光滑条件.

2.1.3 检验 X′(1)是否具有指数规律 准指数规律检验公式为∶

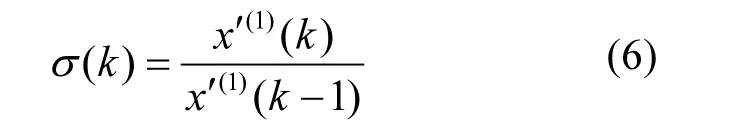
当σ(k)∈[1,1.5]可以建立GM(1,1)模型,其结果见表3.

表3 准指数规律检验Table 3 Quasi exponential law test

由表3可以看出,当k>2后满足准指数规律.

2.1.4 确定数据矩阵B,Y

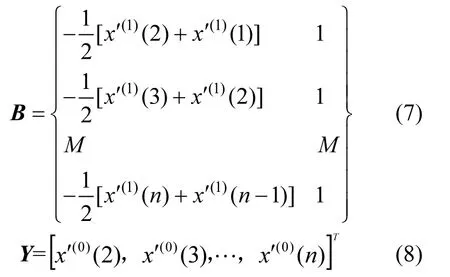
2.1.5 计算参数列ˆa

2.1.6 确定微分方程,求时间响应函数 白化微分方程为∶

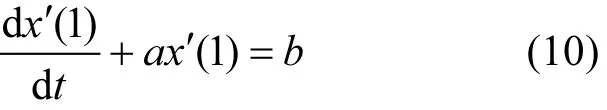
白化微分方程的解,即时间响应函数∶

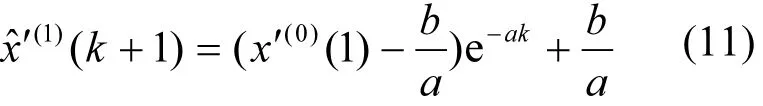
计算可得∶

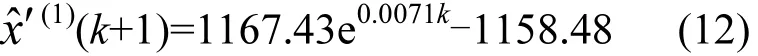
拟合结果见表4.

2.1.7 精度检验 由表4、表5可得,溶解氧的平均相对误差为5.8%为3级精度,采用后验差法对模型群进行均方差比值分析为0.64为3级精度,采用后验差法对模型群进行小误差概率分析为0.89为2级精度.GM(1,1)模型预测精度勉强合格,但有待于改进,因此后续使用马尔科夫链进行修正预测.

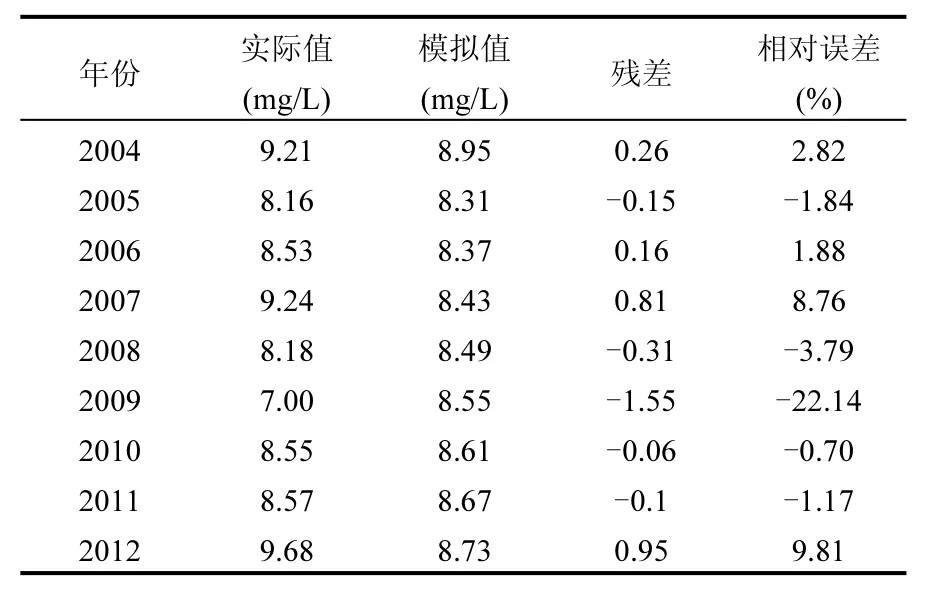
表4 拟合结果Table 4 The fitting results

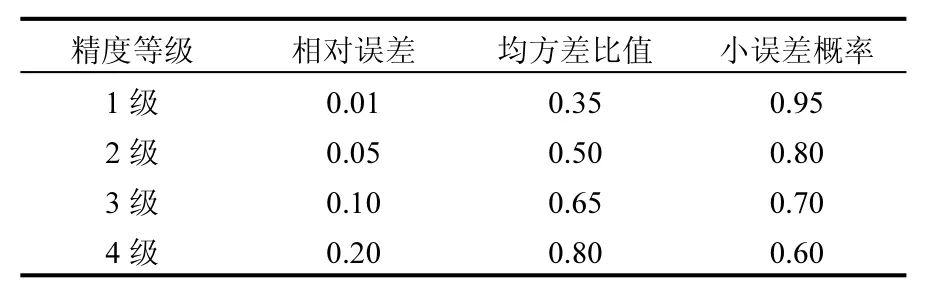
表5 精度检验等级参照Table 5 Testing of the accuracy grade reference table

2.2 马尔科夫链的基本原理

马尔可夫过程是具有所谓马尔可夫性的一类特殊的随机过程.它既适合于时间序列,又适合于空间序列.其基本特征是无后效性,即当系统在某时刻ti所处的状态已知,系统在时刻t,t>ti处的状态只会与系统在时刻 ti处的状态有关,与系统在时刻ti之前的状态无关.

马尔可夫过程称为马尔科夫链.一个n阶马尔科夫链由n个状态集合{E1,E2,…,En}和一组转移概率 pij{i,j=1,2,…,n}确定.转移概率pij{i,j=1,2,…,n}反应了各种随机因素的影响程度,故马尔科夫链可用于随机波动性较大的问题,在这一点上可以弥补灰色模型的不足.

2.3 模糊分类

模糊分类是以模糊集合论作为基础,运用数学模型计算它对于所有集合的隶属度,然后根据隶属度的大小确定分类归属的一种针对不确定事物的分析方法[17].

将原始时序数据与灰色预测曲线的相对残差作为划分标准,将系统划分为m个状态,任意一个状态可以表示为

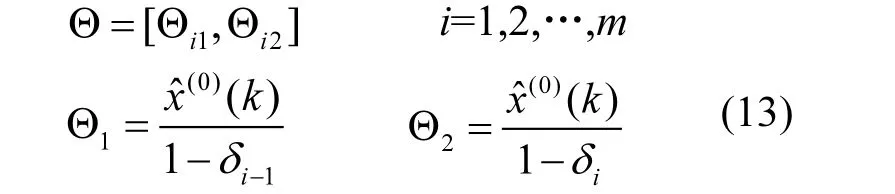
式中,δi-1、δi分别为第 i个划分标准的相对残差上下界限;而Θi-1、Θi分别为第i个状态的取值区域上下界限.

根据马尔科夫链随机过程分析方法的应用经验及相对残差幅度分布情况,可做如下状态划分.

状态 1∶相对残差幅度<-24%,表示极度高估状态,该年为强下降年份.在9年中没有出现这种极端情况.

状态2∶相对残差幅度为-24% ～ -8%,表示高估状态,该年为弱下降年份.

状态3∶相对残差幅度为-8% ～ 8%,表示一般状态,该年为正常年份.

状态4∶相对残差幅度为8%～24%,表示低估状态,该年为弱上升年份.

状态5∶相对残差幅度>24%,表示极度低估状态,该年为强上升年份.在9年中没有出现这种极端情况.

由于不存在处于状态1和状态5的预测点,因此仅考虑状态 2、3、4,将每个状态定义为模糊集,用三角形法构造每个模糊集的隶属函数,如下式.

根据隶属函数计算出每点数据的模糊状态向量,根据最大隶属原则确定每点数据所属状态,统计出系统状态转移情况(表6),并由此得到状态转移矩阵P.

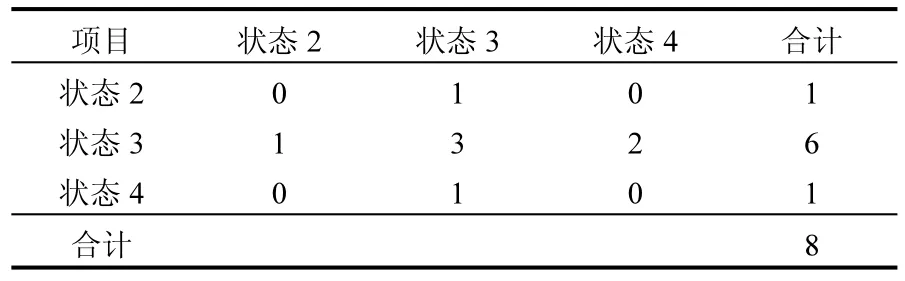
表6 状态一步转移次数统计Table 6 The statistics of state step transfer frequency

状态转移概率∶

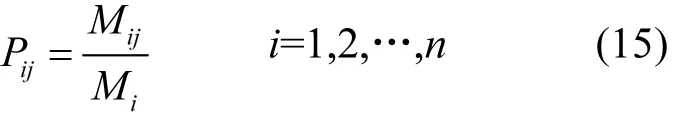
式中,Mij为由状态Θi经过1步转移到状态Θj的原始数据的个数;Mi为处于状态 Θi的原始数据个数;Pij为由状态Θi经过1步转移到状态Θj的概率.

概率状态矩阵∶

故∶

2.4 预测

2011年相对残差为-1.17%,计算的其状态模糊向量为(0.075,0.925,0).应用马尔科夫链计算出2012～2016年模糊状态向量,再通过加权求和法算出相对残差预测值[18-20],最后得到预测结果.预测结果如表7.溶解氧浓度的变化趋势如图2所示.

由图2可以看出,2004～2016年DO的浓度虽有小幅波动,但总体呈上升趋势,且都维持在8mg/L以上,因此该指标优于一级标准(7.5mg/L),预计2016年将达到9.15mg/L.DO浓度上升的原因可能是有关部门采取的一系列治理海河的措施取得了成效使海河水质有所好转.

表7 海河三岔口断面溶解氧浓度预测结果Table 7 Forecasting values of DO at three fork section of Haihe River

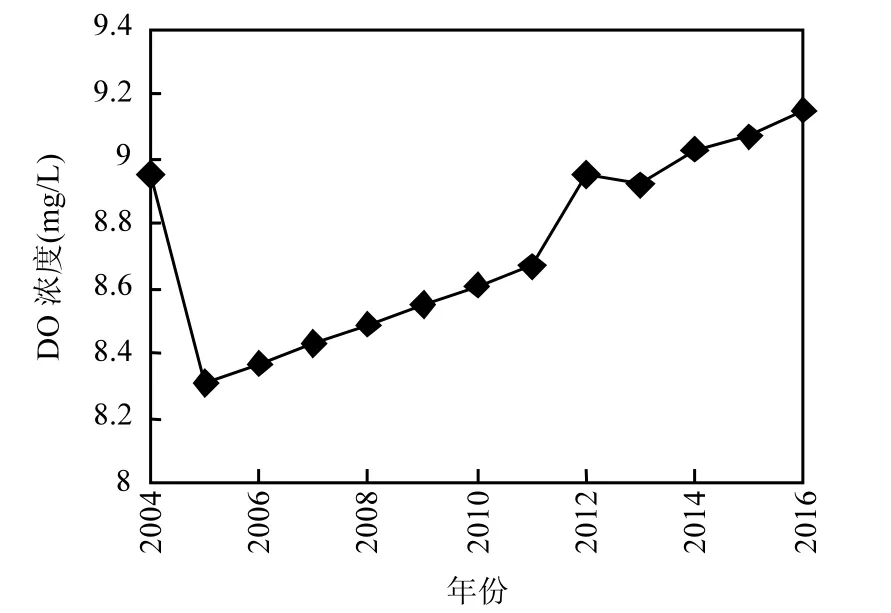
图2 溶解氧浓度变化趋势Fig.2 The tendency change of DO’s concentration

应用灰色模糊马尔科夫链预测海河三岔口断面的CODMn浓度和NH3-N浓度大小,计算过程同上,CODMn的原始数据及 GM(1,1)模型的拟合计算结果见表8,NH3-N的原始数据及GM(1,1)模型的拟合计算结果见表9.

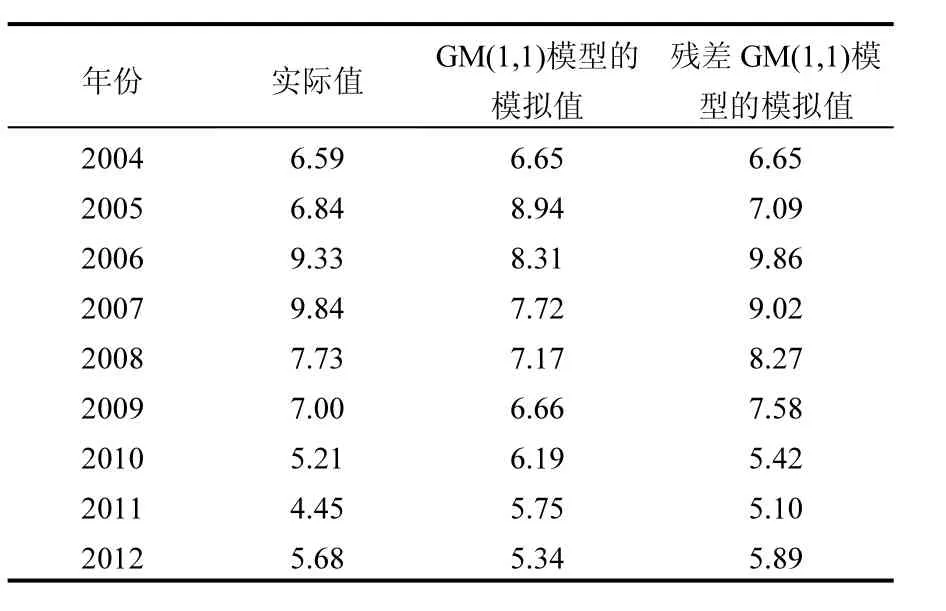
表8 2004～2012年海河三岔口断面高锰酸盐指数的实际值及GM(1,1)与残差GM(1,1)模型的模拟值(mg/L)Table 8 The concentration and the fitting results of CODMnat three fork section of Haihe River during 2004～2012 (mg/L)

其中高锰酸盐指数浓度的模拟结果的平均相对误差为 0.15,氨氮浓度的模拟结果的平均相对误差为 0.22,均不符合精度要求.故采用残差修正模型对原模型进行修正[21].具体过程如下∶

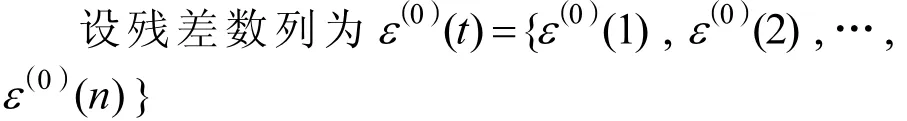
对ε(0)（t） 建立 GM(1,1)模型,其时间响应函数为∶

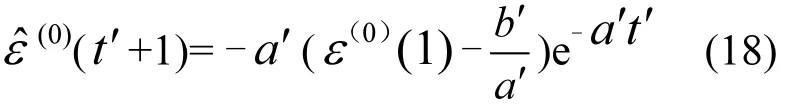
将残差GM(1,1)模型代入原模型∶

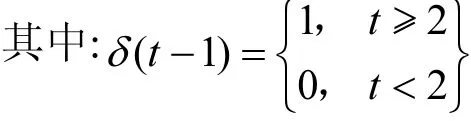
CODMn的残差修正模型的模拟值见表8,NH3-N的残差修正模型的模拟值见表 9.高锰酸盐指数及氨氮浓度的模拟结果的平均相对误差均为0.05,均符合精度要求.马尔科夫链的预测结果如表10所示.

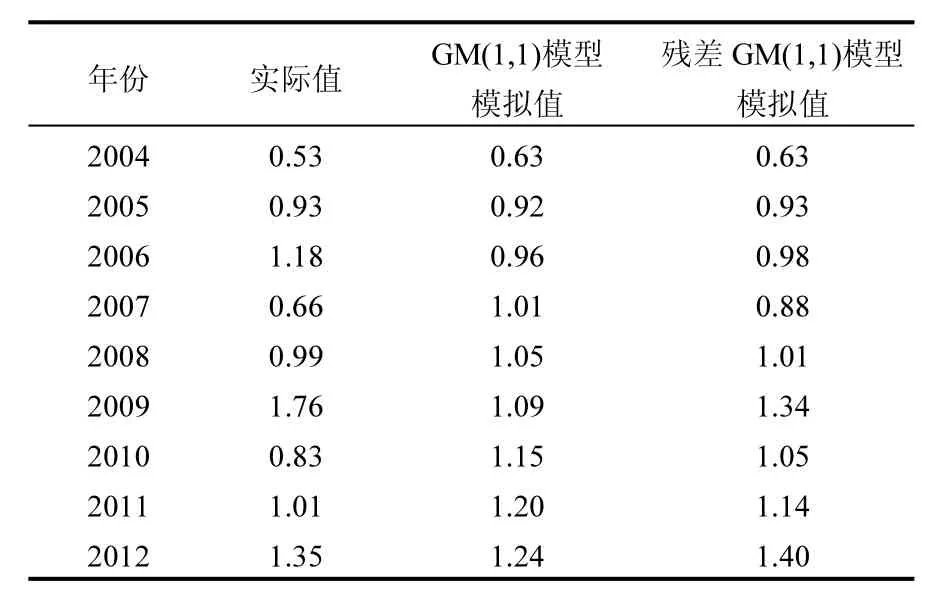
表9 2004～2012年海河三岔口断面氨氮浓度的实际值及GM(1,1)与残差GM(1,1)模型的模拟值(mg/L)Table 9 The concentration and the fitting results of NH3-N at three fork section of Haihe River during 2004～2012 (mg/L)

高锰酸盐指数浓度和氨氮浓度的变化趋势如图3所示.

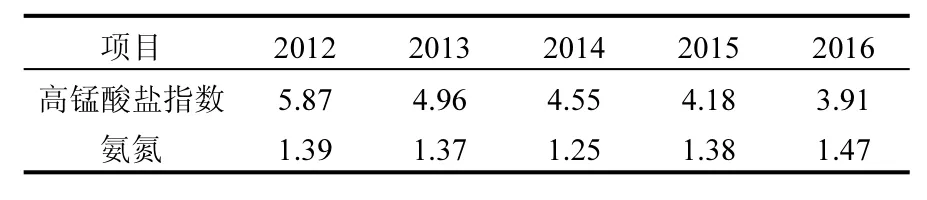
表10 海河三岔口断面的高锰酸盐指数及氨氮浓度马尔科夫链预测结果(mg/L)Table 10 Forecasting values of CODMnand NH3-N at three fork section of Haihe River (mg/L)

图3 高锰酸盐指数浓度和氨氮浓度的变化趋势Fig.3 The tendency change of CODMnand NH3-N’s concentration

由图 3可以看出,2004～2016年 CODMn和NH3-N的浓度均有小幅波动,但总体上 CODMn浓度呈下降趋势,NH3-N 浓度呈上升趋势. CODMn浓度一直保持在远低于一级标准规定的15mg/L,预计2016年将达到3.91mg/L,由于不可能无限降低,预计几年后将会趋于一较小值. NH3-N浓度一直在0.5mg/L以上,劣于国家一级标准,若不加以控制,预计 2016年将达到1.47mg/L.CODMn浓度下降的原因也应是治理海河的措施取得了良好效果,NH3-N浓度上升的原因可能是所采取的措施主要是针对点源污染,而海河水体中的氨氮还有很多来自非点源污染,这部分污染源并未得到有效控制.

用2012年的数据对模型精度进行对比验证,由表4及表7计算可得,DO的GM(1,1)模型与GM(1,1)-马尔科夫链预测模型模拟结果的相对误差分别为 9.81%,7.5%;由表 8及表 10可得, CODMn的 GM(1,1)模型,残差 GM(1,1)模型与GM(1,1)-马尔科夫链预测模型的相对误差分别为5.99%,-3.7%,-3.35%;NH3-N的GM(1,1)模型,残差 GM(1,1)模型与 GM(1,1)-马尔科夫链预测模型的相对误差分别为 8.15%,3.7%,2.96%.3项指标均为 GM(1,1)-马尔科链夫预测模型的相对误差最低,预测精度最高,其结果更具有效性.

3 结论

3.1 使用 GM(1,1)预测模型对海河三岔口断面的 DO、CODMn和 NH3-N 3项指标进行模拟时,DO的模拟结果勉强符合精度要求,CODMn和NH3-N均不符合精度要求.分析原因可能是原始数据波动性较大,且灰色预测存在灰色偏差与抗干扰能力弱的问题.

3.2 通过对模型精度进行对比验证,GM(1,1)-马尔科夫链预测模型的相对误差最低,预测精度最高,说明其预测结果更具有效性、合理性.分析原因是马尔科夫链可用于随机波动性较大的问题,这一点上可以弥补灰色模型的不足.

3.3 经预测,海河三岔口断面的 DO浓度及NH3-N浓度呈上升趋势,CODMn浓度呈下降趋势.DO及 CODMn一直优于国家一级标准,而NH3-N一直劣于国家一级标准.预计 2016年DO、CODMn和NH3-N浓度分别可达9.15,3.91, 1.47mg/L.虽然海河的治理措施取得了一定效果,但仍需进一步整治,尤其是对NH3-N浓度的控制,不仅针对点源污染,非点源污染也应采取相应治理措施.

[1] 刘子岩,罗固源,吕青峰,等.灰色模型理论对长江次级河流水质污染的短期预测模拟 [J]. 三峡环境与生态, 2011,33(3)：47-50.

[2] 冉延平,何万生,雷旭晖.应用灰色GM(1,1)模型及其改进模型预测渭河天水段水质 [J]. 水资源与水工程学报, 2011,22(5)：88-91.

[3] 邱 林,黄 鑫,李洪良.基于模糊权马尔可夫模型的综合水质预测 [J]. 人民长江, 2007,38(1)：75-77.

[4] 李如忠.水质预测理论模式研究进展与趋势分析 [J]. 合肥工业大学学报, 2006,29(1)：26-30.

[5] 邹志红,王乐娟.湖泊富营养化趋势的灰色马尔柯夫预测 [J].环境科学学报, 2009,29(2)：427-432.

[6] 王泽斌,马 云,叶 珍,等.应用 GM(1,1)模型预测阿什河水质变化趋势 [J]. 环境科学与管理, 2011,36(4)：24-39.

[7] 邓 婵,张新政,罗作煌,等.灰色神经网络组合模型在区域水质预测中的应用 [J]. 科学技术与工程, 2009,9(9)：2457-2458.

[8] LIU S F,DENG J L.The rang suitable for GM(1,1) [J]. Journal of Grey System, 1999,11(1)：34-37.

[9] Deng J L. Spectrum mapping in grey theory [J]. The Journal of Grey System, 2000,12(2)：116-120.

[10] 孙盼盼,李洪波.基于灰色模糊马尔可夫链的中国出境旅游规模预测 [J]. 乐山师范学院学报, 2010,25(12)：39-42.

[11] 高 蔚.基于 Markov理论的改进灰色 GM(1,1)预测模型研究[J]. 计算机工程与科学, 2011,33(2)：159-163.

[12] Wang Z X, Hipel K W, Wang Q, et al. An optimized NGBM(1,1) model for forecasting the qualified discharge rate of industrial wastewater in China [J]. Applied Mathematical Modelling, 2011, 35(12)：5524-5532.

[13] 王 宏,杨霓云,沈英娃,等.海河流域几种典型有机污染物安全性评 [J]. 环境科学研究, 2003,16(6)：35-37.

[14] Gao X L, Chen C T A. Heavy metal pollution status in surface sediments of the coastal Bohai Bay [J]. Water Research, 2012, 46(6)：1901-1911.

[15] Liu Jia Hong, Qin Da Yong, Wang Hao, et al. Dualistic water cycle pattern and its evolution in Haihe River basin [J]. Chinese Science Bulletin, 2010,55(16)：1688-1697.

[16] 郭锐利,郑钦玉,刘 娟,等.基于熵值法和 GM(1,1)模型的重庆城市生态系统健康评价 [J]. 中国环境科学, 2012,32(6)：1148-1152.

[17] 谢建文,张元标,王志伟,等.基于无偏灰色模糊马尔可夫链法的铁路货运量预测研究 [J]. 铁道学报, 2009,31(1)：1-7.

[18] 赵琳琳,夏乐天.灰色马尔可夫链模型的改进及其应用 [J]. 河海大学学报, 2007,35(4)：487-490.

[19] 游 珍,杜传亮,李永涛.基于灰色-马尔可夫耦合模型的区域建设用地需求预测 [J]. 生态环境, 2007,16(5)：1528-1532.

[20] Wei H, Yang H S, Tian D P, et al. Dam safety monitoring model mased on Markov Chain [J]. Advanced Materials Research, 2011,255(4)：3626-3631.

[21] 尚晓锶,林卫东,唐艳葵,等.指数平滑和 GM(1,1)组合法在水质预测中的应用—以邕江水源地铁、锰浓度为例 [J]. 环境科学与技术, 2011,34(1)：191-195.

Water quality prediction of Haihe River using grey-fuzzy-markov chain model.

YU Hui, SUN Bao-sheng*, LI Ya-nan, ZHANG Yan, QI Geng-shen
(School of Environmental Science and Engineering, Tianjin University, Tianjin 300072, China). China Environmental Science, 2014,34(3)：810～816

The GM(1,1) model has been widely used in the prediction of water quality. But it had the disadvantages of grey bias and weak anti-jamming capability. To solve this problem, the markov chain theory and fuzzy classification were introduced into the grey forecasting model and a new method named the Grey-Fuzzy-Markov Chain Model was proposed. In this paper, the tendency changes of DO,CODMnand NH3-N’s concentration were predicted in Haihe River from 2012 to 2016. The results showed that from 2004 to 2016 the concentration of DO and NH3-N would increase to 9.15 and 1.47mg/L respectively in 2016. Meanwhile the CODMnwould decrease to 3.91mg/L in 2016. The concentration of DO,CODMnand NH3-N in 2012 were forecasted to check the precision of this model. The precision of the Grey-Fuzzy-Markov model was better than the GM(1,1) model and it would be a scientific method for the prediction of water quality.

GM(1, 1) model；fuzzy classification；Markov Mode

X824

：A

：1000-6923(2014)03-0810-07

于 慧(1989-),女,山东德州人,天津大学硕士研究生,主要从事环境影响评价研究.

2013-07-10

天津市自然科学基金重点资助项目(07JCZDJC02100)

* 责任作者, 副教授, baosheng_sun@sina.com