基于环境基尼系数最小化模型的水污染物总量分配优化——以张家港平原水网区为例

田 平,方晓波,王飞儿,朱 瑶

(1.浙江大学环境与资源学院,浙江 杭州 310012；2.浙江农林大学环境与资源学院,浙江 临安 311300；3.浙江卓锦工程技术有限公司,浙江 杭州 310004)

基于环境基尼系数最小化模型的水污染物总量分配优化
——以张家港平原水网区为例

田 平1,3,方晓波2*,王飞儿1,朱 瑶1

(1.浙江大学环境与资源学院,浙江 杭州 310012；2.浙江农林大学环境与资源学院,浙江 临安 311300；3.浙江卓锦工程技术有限公司,浙江 杭州 310004)

本文通过应用 WASP模型计算出研究区域环境容量及其在各镇的空间分布,在此基础上确定整个区域的污染物目标总量.结合研究区域实际情况,提出并开发了基于经济、社会和资源禀赋的综合环境基尼系数最小化模型,用于污染物目标总量分配的最优化求解.最终分配方案相比污染物现状排放、容量分配两种情形而言,COD的基尼系数分别下降15.1%和8.4%,氨氮的基尼系数分别下降11.0%和13.7%,分配方案更加公平、合理.在最终优化分配所得的COD削减方案中,长泾镇削减比率最高,达到20%,削减量为231.74t/a;在相应的氨氮削减方案中,祝塘镇削减比率最高,达到59.9%,削减量为59.74t/a.

基尼系数；最小化；总量分配；环境容量；WASP模型

在过去的几十年里,总量控制技术被广泛应用于发达国家水质管理领域,对于改善水环境质量起到了明显的作用,如莱茵河的 RAP(Rhine Action Programme)[1]、多瑙河的DRBPRP (Danube River Basin Pollution Reduction Programme)[2]、日本的TPLCS(Total Pollutant Load Control System)[3]以及美国的TMDLs(Total Maximum Daily Loads)[4].我国将总量控制技术与水污染防治规划相结合,逐步形成了以污染物目标总量控制技术为主,容量总量控制和行业总量控制为辅的水质管理技术体系,为我国水环境管理基本制度的建立奠定了基础[5].

污染物目标总量在特定的时间和区域内是一定的,可将其视作一种与水、土地等同样稀缺的资源,在经济发达地区,这种稀缺性更加明显

[6-9].在我国现行的水环境管理体制下,还无法完全实现按照水环境容量进行污染物目标总量的分配,在实际实施过程中还需要综合考虑经济、社会等因素,是一个主客观相结合的决策过程.如何通过一些技术手段使这个决策过程中主观因素更小,污染物目标总量更公平、合理地分配到各个行政单元显得尤为重要,直接影响了总量控制方案的可操作性.

流域污染物目标总量分配往往以经济最优化为目标,以公平性与效率性为决策准则进行污染负荷分摊,常用方法包括等比例分配、模糊多目标、基尼系数等[10].在以经济最优化为目标的分配中,由于片面强调整体的经济效益性,忽视了区域间客观存在的差异性,导致分配结果不公平,影响目标总量控制工作顺利开展[11],而基于基尼系数的污染物目标总量分配以公平性为原则,能合理地将污染物分配到各个行政单元,成为一种推广应用的的污染物分配方法,并成功应用于巢湖[11]、松花江[12]、海河流域[13]、汤逊湖[14]等流域污染物分配研究,为流域污染物优化分配提供参考.

我国太湖流域近年来水污染问题尤为突出

[15].国家于 2008年 5月出台了《太湖流域水环境综合治理总体方案》[16],其实质是一个针对太湖流域的新型总量控制计划.张家港河流域属于太湖流域的沿江水系,对太湖水质产生一定的影响,然而未见该流域污染物总量分配文献报道.本研究以太湖流域典型的平原水网区—江阴市张家港河流域为研究对象,在基于WASP模型水环境容量计算基础上,结合该区域的自然、社会、经济等特点,提出并开发了基于GDP、人口、土地面积和环境容量的综合环境基尼系数最小化模型,基于该模型确定最优的目标污染物总量分配及削减控制方案.

1 研究区概况

图1 研究区域示意Fig.1 Sketch map of the study area

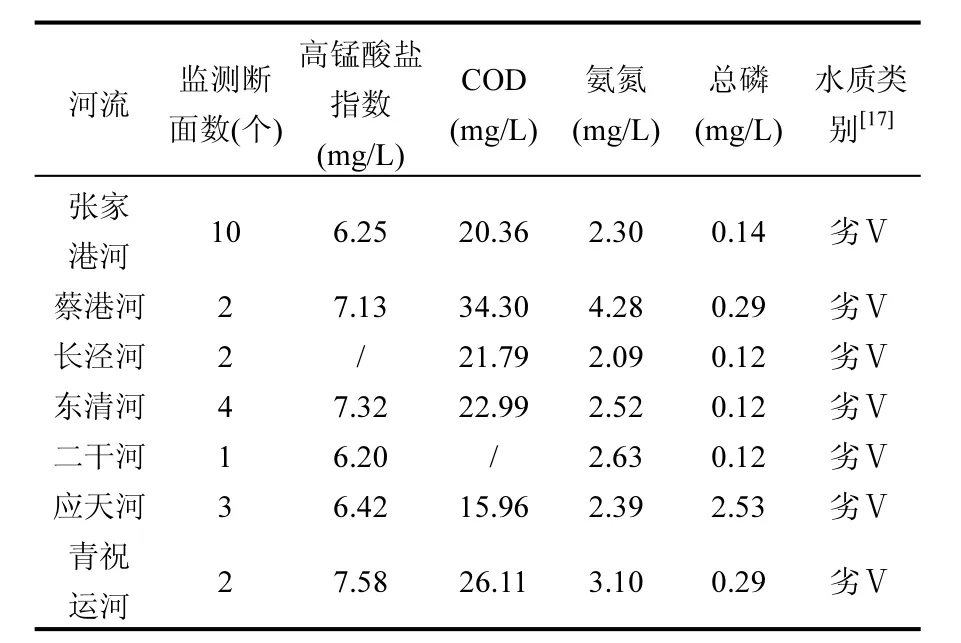
表1 研究区域水环境质量监测结果Table 1 Environmental quality of the water bodies in the study area based on routine monitoring data (2009)

研究区域位于江苏省江阴市东部,主要由张家港河、蔡港河、长泾河、应天河、二干河、青祝运河、东清河等河流组成,包括江阴市周庄、华士、新桥、顾山、长泾和祝塘等乡镇(图1).张家港河为该水系干流,北起长江,经张家港市、江阴市入常熟市,连接“引江济太”骨干通道望虞河.研究区域总面积332.6km2,属典型的平原河网区,地势平坦、河流密度大,年平均降水量 1057mm,年平均气温15.24℃,多年平均径流深431mm,属多水带.区域城镇化水平高、人口密集,经济发展迅猛,2008年末,总人口 38.57万,地区生产总值474.49亿元,人均生产总值12.3万.伴随着社会经济的快速发展,大量污染物排入水体,导致区域水环境质量堪忧,根据江阴市环境监测站2009年的监测数据显示,张家港河干流及主要支流水质超标严重,尤以氨氮指标最为突出(表1).

2 研究方法

2.1 基于环境基尼系数的污染物总量优化分配模型

2.1.1 环境基尼系数 环境基尼系数原理与基尼系数[18-19]基本一致,其体现了人口、GDP、环境容量等指标与污染物排放量之间的比值,该比值越小则污染物排放分配越公平[20].在经济学上,基尼系数小于0.4作为收入分配差距的警戒线,小于0.4认为分配合理. 在环境问题中,由于所选取指标存在无资源冲突、无不平等前提,因此环境基尼系数可能趋于 0[20-21].借鉴相关文献[12,20-21]报道,本研究环境基尼系数合理范围界定为0～0.2.

2.1.2 环境基尼系数评价指标确定 合适评价指标的选取是保障基尼系数污染物总量分配公平合理的前提,经济、生态、社会等因素都会影响污染物总量分配.本研究针对张家港市实际情况,选取地区生产总值(GDP)、人口数量(P)、土地面积(S)和环境容量(C)这4项指标来评估污染物分配方案的公平性[22].

人口是一个代表社会发展水平的指标.选择人口作为评价指标,一方面流域中每个人都有享受向周围水体排放污水的权利,另一方面江阴市近 60%的 COD排放来源于城市生活污水,因此该指标基尼系数越小表明该流域人民享受向周围水体排放污染物的权利越均等.

GDP是一个反映当地经济发展水平的指标.GDP增长会导致该区域污染物排放量增加,同时,GDP增速快的区域能投入更多财力保障污染物削减方案及管理措施的实施,因此,降低单位 GDP污染物排放量能有效地降低该指标基尼系数.

环境容量是一个代表资源禀赋及反映环境承受及自净能力的指标.本论文涉及的水环境容量是指水体在规定的水质目标下所能接纳的污染物最大量.从“效率”角度而言,水环境管理中水体自净能力利用得越充分,污染物对水环境总体影响越小,因此,该指标基尼系数越小,则水环境自净能力利用越充分.

土地面积是一个代表资源禀赋的指标.该指标被纳入评价指标有以下几方面原因∶土地面积与面源污染直接相关,土地面积越大降雨径流带入地表水体的面源污染物越多;土地有自净能力,能去除污水中的污染物;土地面积越大,人口增长、工业发展和经济增长潜力越大;该指标基尼系数越小表明污染物分配越公平.

2.1.3 环境基尼系数计算模型 本研究以张家港河流域各乡镇为环境基尼系数计算基本单元.先将各乡镇各环境指标所承载的污染物按照由低到高的顺序排列,采用梯形面积法计算环境基尼系数,公式如式(1)[20]∶

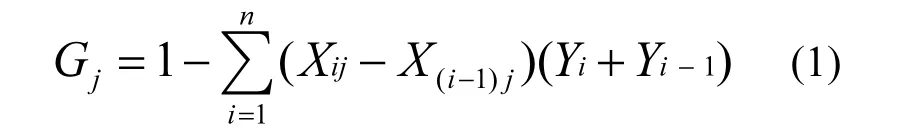
式中∶j为 GDP、人口、土地面积和环境容量 4个指标编号;i为乡镇编号,i=1,2,…,n; Gj为基于环境指标j的基尼系数;Xij为第i个乡镇环境指标j的累积比例,%;Yi为第 i个乡镇排放或分配污染物量的累积比例,%;当i=1时,X(i-1)j=0,Yi-1=0.

2.1.4 综合环境基尼系数最小化模型构建 基于对研究区域污染现状的分析和政府总量控制的要求,本研究选取 COD和氨氮作为目标总量控制污染物来构建环境基尼系数模型,以GDP、P、S和C为评价指标,在权重设置和各项指标环境基尼系数模型构建基础上,再构建综合环境基尼系数最小化模型. 并在Excel平台上进行二次程序开发以求解,其主要思路是对决策变量即污染物目标总量在各单元的分配设置一个步长,在一定的边界条件下,以设定步长为单位进行循环计算,直至使综合基尼系数最小为止.

根据江阴市污染源普查结果,结合未来产业规划的需要,确定在 COD的分配中,各项指标权重分别为 GDP(0.3)、P(0.3)、S(0.1)和 C(0.3);在氨氮的分配中,各项指标权重分别为GDP(0.2)、P(0.3)、S(0.2)和C(0.3).

由于程序开发基于循环运算的思路,因此需要设定决策变量循环步长、取值范围等边界条件来控制计算量.根据研究区域目标总量结果和现状排放量数据,确定边界条件如下∶

(1) 各镇相对现状排放削减比例,COD不超过20%,氨氮不超过60%.即∶

式中,Tk表示分配到第 k个镇的污染物目标总量,T0k表示第k个镇目前污染物的排放量(下同).

(2) 研究区域内目标总量一定,即污染物目标总量=基于WASP模型的环境容量× (1-安全临界值),即 COD目标总量=6604.49×(1-5%)=6274,氨氮目标总量=291.91×(1-5%)=277.

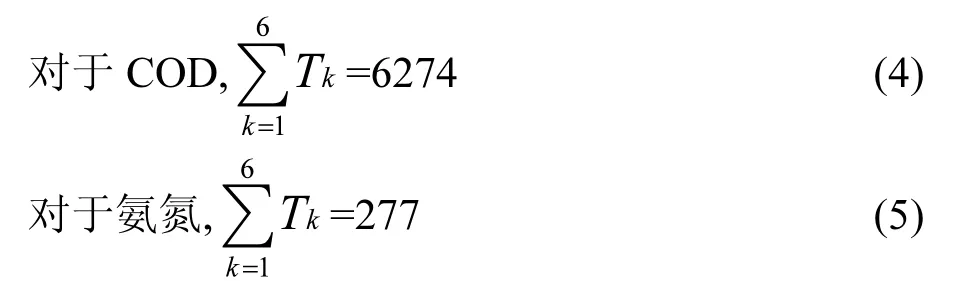
(3) 决策变量COD的循环步长设置为20t/a,氨氮的循环步长设置为10t/a.

根据环境基尼系数的原理,即基尼系数越小、分配越公平,确定以综合基尼系数最小为目标函数,即∶

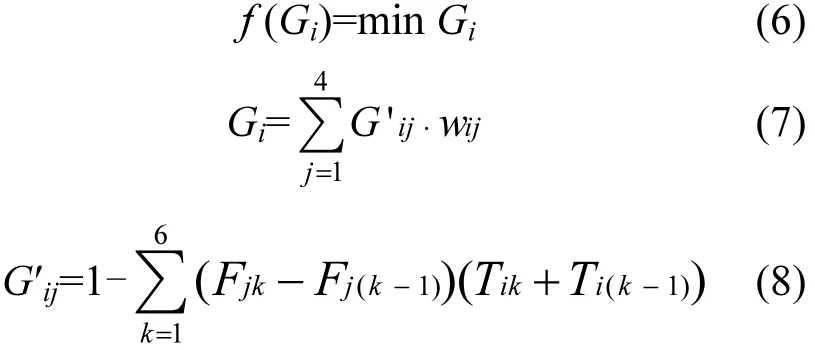
式中,f为目标函数,即综合基尼系数最小值;G为总量污染物综合基尼系数;G′为总量污染物对于各指标的单项基尼系数;w为综合基尼系数中各单项基尼系数的权重;F为单项指标;i为总量污染物的编号;j为单项指标的编号.

2.2 基于WASP的水环境容量分析模型

水环境容量不仅是污染物目标总量分配的重要参考指标,也是用以确定污染物目标总量的基础. 其原理是在选定水质模型及其参数率定的前提下,建立负荷——水质响应关系,输入限制条件,计算划定水域的水体纳污能力.本研究选用美国环保署(USEPA)推荐的 WASP7.3模型为水环境容量计算工具.WASP水质模型被称之为“万能水质模型”[23],能实现河流、河口、湖泊等不同水体一维、二维、三维水质模拟,在土耳其布尔萨Uluabat湖[24]、台湾高雄Salt-water河[25]、浙江省湖州市太湖河网区[26]等水体环境容量估算及负荷削减等流域水质管理中得以应用.

2.2.1 WASP模型 WASP模型由DYNHYD、EUTRO和TOXI 3个子模型组成,DYNHYD模型用于模拟河流流量和流速,EUTRO模型用于模拟氧、碳、氮和磷等富营养化指标迁移转化规律,TOXI模型可以模拟水体中悬浮固体、盐和重金属等迁移转化[27].WASP模型模拟步骤如下∶首先通过N天DYNHYD模型模拟,明确模拟河段流量、流速、河段水体体积和上游来水等相关信息,在此基础上分别采用EUTRO和TOXI子模型进行相应水质模拟[27].本研究根据张家港河水体实际污染情况,选择COD和氨氮为环境容量计算指标,采用WASP模型中EUTRO子模型对张家港河水质进行模拟.为简化研究区模拟计算过程,模型运行过程中进行一些假定,具体假定内容见文献[26].

2.2.2 基于WASP模型的水环境容量计算 张家港河流域为平原河网区,河道流速较缓慢且流向不定,借鉴往复流河道水环境容量计算方法,基于WASP7.3模型,以张家港平原河网区域90%水文保证率流量及地表水Ⅳ类水质要求为基础,采用试错法进行水环境容量计算. 水环境容量计算公式见文献[26].

2.2.3 污染物入河量估算 研究区污染源包括工业点源、城市污水处理厂、规模化畜禽养殖场等点源,以及农村生活污染、分散养殖、种植业、水产养殖等面源. 污染物入河量估算,点源按照就近原则排入相应河道,面源采用排污当量系数法估算,并结合地表径流流向根据河道长度均匀地进入相应河道[26].污染物入河量计算公式、污染物排污当量、污染物入河系数借鉴文献[26,28]. 2.2.4 数据来源 容量计算所需污染源基础数据来源于江阴市污染源普查和江阴市环保局环境统计资料;水质数据来源于江阴市环境监测站 2005～2009年实测数据;河道及水文资料来源于江阴市水利局;降雨量及其气象资料来源江苏省气候中心.

3 结果与讨论

3.1 水环境容量

3.1.1 WASP参数率定结果 根据张家港河流域水力学特征及支流、概化后排污口位置,把研究区域河网划分为244个400～500m的河段.自此基础上,选用水质监测数据较为完整的凤凰、陆桥、北国大桥、北新桥4个断面作为率定和验证断面,在参数取值范围内,输入2005～2008年枯水期(12月、1月及2月)COD和氨氮实测值,不断调整模型参数直到模拟值接近实测值. 由于污染负荷以 CODCr作为输入条件,而水质以CODMn作为模型率定和验证条件,两者必须进行转化,根据流域内实测资料确定CODCr和CODMn之间的转化系数为 3.44.优化后参数取值如表 2所示,表2中未列出参数为模型默认值.

表2 研究区域WASP模型水质参数值Table 2 Parameters of the WASP model for the study area

图2 90%保证率COD、氨氮率定结果Fig.2 Calibration results of COD and ammonia nitrogen under the 90% hydrological guarantee rate

在参数率定基础上,以2009年枯水期COD和 氨氮实测值,采用线性回归法和一致性指数法[31]评价模型率定效果,一致性指数(d)按下式计算∶

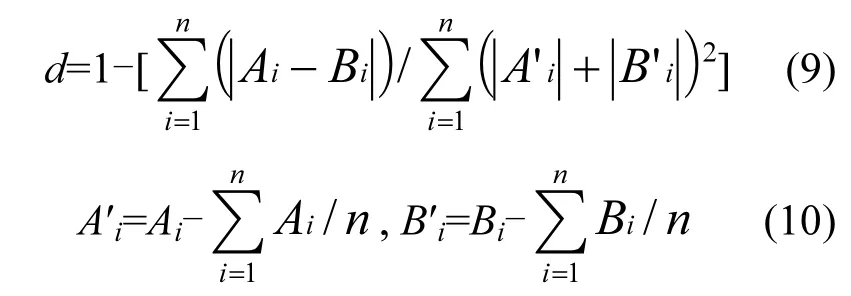
式中,n为样本总数,Ai为模拟值,Bi为实测值.

表3 率定结果误差分析Table 3 Error analysis of calibration results

由图3可知,在趋势线截距为0的预设条件下,模拟值与实测值的相关性较好(相关性系数>0.85).一致性评价结果显示(表 3),一致性指数(d)均在0.9以上,表明模拟值与实测值接近,COD、氨氮的总体相对误差为 8.48%、14.28%,也均较低,说明优化后的模型参数可用于此流域总量控制研究.

3.1.2 区域水环境容量 根据对该区域几十年的降雨及水文资料的频率分析,经比较选择1971年2月作为90%的水文保证率流量.研究区域河网密布,河流数量众多,不利于容量计算,为此,根据河网概化的一般原则[26,32],结合掌握的水文资料,以区域内张家港河等13条主干河流为基础进行概化.经计算,本区域内 COD和氨氮的总环境容量为 6604.49t/a,291.91t/a,其在各镇的具体情况见表 4.根据对江阴市污染源普查及环境统计数据的分析计算,本研究区域2009年COD和氨氮的入河量分别为 6894.03t,492.34t,均超过环境容量值(COD 6604.49t/a,氨氮 291.91t/a),氨氮入河量更是超环境容量的 69%,这与研究区域水质氨氮超标严重的现状相吻合.

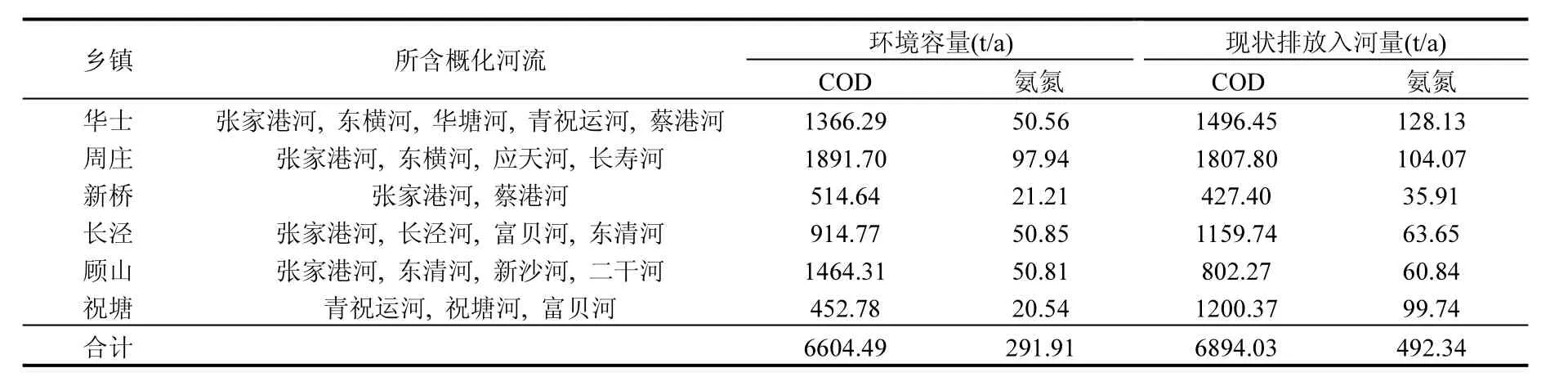
表4 研究区域各镇环境容量及污染物现状排放入河量Table 4 Environmental capacity and output load of the 6towns in the study area

3.2 目标总量分配

表5 研究区各镇污染物目标总量及削减比率Table 5 Aimed total pollutant load and reduced rate of every town in research area

根据WASP模型容量计算结果,借鉴TMDL的做法,考虑安全临界值(MOS)[33],确定本区域污染物目标总量.根据区域实际特点,取模型计算环境容量的 5%作为安全临界值,考虑模型计算方便,将结果进行取整,最终确定区域污染物目标总量为 COD 6274t/a,氨氮277t/a.在此基础上,结合区域经济发展水平和实际承载能力,同时确保实现总量削减目标,确定各乡镇COD削减上限不超过20%,氨氮削减上限不超过60%,并保证基于GDP、P、S和C 4个指标的基尼系数总和最小,基于综合环境基尼系数最小化模型,并通过Excel平台上二次开发的程序,把污染物目标总量合理地分配到各乡镇.

根据模型运行结果,研究区域污染物目标总量(COD 6274t/a,氨氮277t/a)在6镇的分配结果如表5所示.该分配方案与基于容量的总量指标分配、污染物现状排放入河量2种情形下环境基尼系数的对比情况如表6所示.

表6 不同阶段总量控制污染物分配的单项及综合基尼系数比较Table 6 Comparison of the single and integrated Gini Coefficients of the allocation of total pollutants in different phases

3.3 讨论

由表4可知,各乡镇COD环境容量大小依次为∶周庄镇>顾山镇>华士镇>长泾镇>新桥镇>祝塘镇;氨氮环境容量大小依次为∶周庄镇>长泾镇>顾山镇>华士镇>新桥镇>祝塘镇. 通过综合环境基尼系数最小化模型优化分配,各乡镇目标总量有所变化(表 5),COD目标总量大小依次为∶周庄镇>华士镇>祝塘镇>长泾镇>顾山镇>新桥镇;氨氮目标总量大小依次为∶周庄镇>华士镇>顾山镇>祝塘镇>长泾镇>新桥镇.由表5可知,基于目标总量的各乡镇减排任务,长泾镇COD减排任务最重,占总削减量的20%,这跟其以印染、造纸为主的产业特征及较小的目标总量有关;而华士、顾山两镇COD无需减排,这主要是由于华士镇的环境容量较高,经济、社会指标较为领先,导致其目标总量较高;而顾山镇主要是由于目标总量较高,污染物现状排放入河量较小所致.相比COD指标,各镇的氨氮削减任务都比较艰巨,这也从另一个侧面反映了研究区地表水中该指标值高、污染严重的现状.各乡镇氨氮削减比例大小依次为∶祝塘镇>华士镇>长泾镇>新桥镇>周庄镇>顾山镇.祝塘镇和华士镇削减比例大于 50%,为氨氮削减重点镇,祝塘镇由于畜禽养殖业、农业等比较发达,氨氮现状排放量较大,而河流环境容量最小,故其削减任务最为艰巨;而华士镇由于印染、化工等企业众多,氨氮现状排放量最大,导致其削减任务较重.基于综合环境基尼系数最小化模型的最终分配方案并非污染负荷量越大削减比例越高.以氨氮为例,排污大镇周庄镇排放入河量占研究区总量的26.0%,而削减量占总削减量的30.7%;祝塘镇氨氮排放入河量占研究区总量的 7.3%,而削减量却占总削减量的27.7%.虽然周庄镇的氨氮入河量占总量的比例比祝塘镇高出18.7%,但两镇氨氮所需削减量占总削减量的比例接近,主要归因于祝塘镇人口、GDP、环境容量等单位指标所承载的氨氮污染物排放入河量高于周庄镇,这一结果与文献报道研究结果吻合[20]. 因此,本研究所构建的综合环境基尼系数最小化模型综合考虑研究区经济、社会和资源禀赋等客观因素,基于该模型所得到的分配结果更公平合理.

由表 6可知,现状排放基尼系数、容量分配基尼系数和目标总量基尼系数存在差异性. (1)现状排放基尼系数.对 COD而言,基于人口、土地面积的现状排放基尼系数值小于 0.1,而基于GDP、环境容量的现状排放基尼系数值大于0.2,4个指标基尼系数值介于 0.062～0.285之间;对氨氮而言,同样基于人口、土地面积的现状排放基尼系数值小于0.1,而基于GDP、环境容量的现状排放基尼系数值大于0.2,4个指标基尼系数值介于 0.059～0.264之间;表明研究区人均和单位土地面积承载的 COD、氨氮现状排放入河量较均衡,而单位GDP和环境容量所承载的COD、氨氮现状排放入河量不够均衡,存在不公平因素. (2) 容量分配基尼系数.由于Gc与环境容量为同一个指标,因此该值为 0,属于绝对公平;基于GDP-环境容量、人口-环境容量、土地面积-环境容量的COD和氨氮基尼系数值均接近或大于0.2,表明人均 COD和氨氮环境容量以及单位GDP、单位土地面积COD和氨氮环境容量分配不够均衡. (3) 目标总量基尼系数.对COD而言,基于 GDP、土地面积的目标总量基尼系数值小于0.1,而基于人口、环境容量的目标总量基尼系数值接近或大于 0.2,4个指标基尼系数值介于0.041～0.251之间;与现状排放基尼系数进行比较,除了人口-目标总量基尼系数值有明显增大,其余 GDP-目标总量、土地面积-目标总量、环境容量-目标总量3个指标基尼系数值都有不同程度减小,其中 GDP-目标总量基尼系数值减小幅度最大,减少 0.244,并且 4个指标基尼系数值范围,从基于现状排放的 0.062～0.285,变为基于目标总量的0.041～0.251,表明4个指标基于目标总量的基尼系数值范围比基于现状排放趋于更合理区间. 对氨氮而言,基于 GDP、土地面积的目标总量基尼系数值小于 0.1,基于环境容量的基尼系数值为0.14(介于0.1-0.2之间),而基于人口的目标总量基尼系数值大于0.2,4个指标基尼系数值介于 0.076～0.228之间;与现状排放基尼系数进行比较,人口-目标总量基尼系数值有明显增大,土地面积-目标总量基尼系数值略微增加,而GDP-目标总量和环境容量-目标总量2个指标基尼系数值都有减小,GDP和环境容量2个指标基尼系数值分别减少0.171和0.124;4个指标基尼系数值范围从基于现状排放的 0.059～0.264变为基于目标总量的 0.076～0.228,最大值从0.264降为0.228,相对而言4个指标基于目标总量的基尼系数值范围比基于现状排放更为合理.基于GDP、P、S和C 4个指标的COD和氨氮基尼系数总和大小依次均为∶现状排放>容量分配>目标总量. 4个指标基于目标总量的基尼系数总和,相比于基于现状排放、容量分配两种情形而言,COD的基尼系数值分别下降 15.1%和8.4%,氨氮的基尼系数值分别下降 11.0%和13.7%,分配方案更加公平、合理,更易为各镇所接受,操作性也更强.

本研究以基于GDP、P、S和C 4个指标的基尼系数总和最小为优化目标,以各乡镇 COD削减上限不超过20%,氨氮削减上限不超过60%为约束条件,各指标的基尼系数在优化过程中出现了不同程度的变化,但未实现 4个指标基于目标总量的基尼系数都小于基于排放现状的基尼系数,这一结果与相关研究结果一致[11,20].笔者认为,由于优化目标和约束条件所限,在追求基尼系数最优和全局分配最为合理的情况下,出现没有使单个或者几个指标达到最优的情况是合理的,若过分强调单个指标基尼系数优化,而忽略全局,必将影响整体分配方案的合理性.目标总量控制是一项长期工程,不能一蹴而就,应充分考虑研究区的社会、经济以及资源禀赋等实际情况,循序渐进,逐步调整优化.

4 结论

4.1 本研究开发了综合环境基尼系数最小化模型,该模型以地区生产总值、人口数量、土地面积和环境容量为评价指标,并融合TMDL总量控制理念,使各指标目标总量基尼系数值更为合理.各指标 COD目标总量基尼系数值大小依次为∶人口数量(0.251)>环境容量(0.196)>土地面积(0.055)>地区生产总值(0.041);各指标氨氮目标总量基尼系数值大小依次为∶人口数量(0.228)>环境容量(0.140)>土地面积(0.096)>地区生产总值(0.076). 基于地区生产总值、人口数量、土地面积和环境容量4个指标的COD和氨氮基尼系数总和,相比于基于现状排放,分别下降 15.1%和11.0%,分配方案更为合理,更易为各镇所接受.

4.2 通过综合环境基尼系数最小化模型,可实现张家港流域各乡镇2009年COD和氨氮排放入河量的优化分配,结果表明∶对 COD排放入河量而言,长泾镇削减比率最高,达到 20%,削减量为231.74t/a;对氨氮排放入河量而言,祝塘镇削减比率最高,达到 59.9%,削减量为 59.74t/a.基于综合环境基尼系数最小化模型的目标总量分配最优化求解,跟以往只是用基尼系数来判断总量分配方案是否合理的做法相比,保证了在一定约束条件下分配方案的最优性.

[1] International Commission for the Protection of the Rhine (ICPR). Upstream Outcome of the Rhine Action Programme [EB/OL]. (2009-06-18) [2012-4-12]. http：//www.iksr.org/index.php?id= 258&L=3&pdfPage=1.

[2] Niemeyer R. Danube river basin pollution reduction programmereport [EB/OL]. (1999-7) [2012-4-10]. http：//www.icpdr.org/ icpdr-pages/dprp.htm.

[3] Matsuda O. Environmental management of coastal seas in Japan [DB/OL]. (2008-10-2) [2012-4-13]. http：//www.cearac-project. org/2ndCEAWS/presen_PDF/.

[4] Hoornbeek J, Hansen E, Ringquist E, et al. Implementing total maximum daily loads： Understanding and fostering successful results [EB/OL]. (2008-12) [2012-4-15]. http：//www.epa.gov/ owow/tmdl/results/pdf/12kentst_tmdl_rpt.pdf.

[5] 孟 伟,张 楠,张 远,等.流域水质目标管理技术研究(Ⅰ)——控制单元的总量控制技术 [J]. 环境科学研究, 2007,20(4)：1-8.

[6] Zhu Y H, Drake S, Lü H S, et al. Analysis of temporal and spational differences in Eco-environmental carrying capacity related to water in the Haihe River basins, China [J]. Water Resources Management, 2010,24(6)：1089-1105.

[7] 夏华永,李绪录,韩 康.大鹏湾环境容量研究Ⅱ：环境容量规划[J]. 中国环境科学, 2011,31(12)：2039-2045.

[8] 张东菊,刘百桥,田秉晖.海河流域各地区水环境容量紧缺度分析 [J]. 河北师范大学学报(自然科学版), 2011,35(1)：98-102.

[9] 许庆明.环境保护和环境容量产权的合理界定 [J]. 中国环境科学, 1999,19(4)：377-380.

[10] Burn D H, Yulianti J S. Waste load allocation using genetic algorithms [J]. Journal of Water Resources Planning and Management, 2001,127(2)：121-129.

[11] 李如忠,舒 琨.基于基尼系数的水污染负荷分配模糊优化决策模型 [J]. 环境科学学报, 2010,30(7)：1518-1526.

[12] 吴悦颖,李云生,刘伟江.基于公平性的水污染物总量分配评估方法研究 [J]. 环境科学研究, 2006,19(2)：66-70.

[13] 王 媛,牛志广,王 伟.基尼系数法在水污染物总量区域分配中的应用 [J]. 中国人口·资源与环境, 2008,18(3)：177-180.

[14] 肖伟华,秦大庸,李 玮,等.基于基尼系数的湖泊流域分区水污染物总量分配 [J]. 环境科学学报, 2009,29(8)：1765-1771.

[15] 马荣华,孔繁翔,段洪涛,等.基于卫星遥感的太湖蓝藻水华时空分布规律认识 [J]. 湖泊科学, 2008,20(6)：687-694.

[16] 李家才.总量控制与太湖流域水污染治理——《太湖流域水环境综合治理总体方案》述评 [J]. 环境污染与防治, 2010, 32(4)：96-100.

[17] GB3838-2002 地表水环境质量标准 [S].

[18] Stefano B, Thomas S. Optimal cycles and social inequality： What do we learn from the Gini index?[J]. Research in Economics, 2006,60(1)：35-46.

[19] Druckman A, Jackson T. Measuring resource inequalities： The concepts and methodology for an area-based Gini coefficient [J]. Ecological Economics, 2008,65(2)：242-252.

[20] 秦迪岚,韦安磊,卢少勇,等.基于环境基尼系数的洞庭湖区水污染总量分配 [J]. 环境科学研究, 2013,26(1)：8-15.

[21] 刘 耀,吴仁海,廖瑞雪.大气污染物总量分配公平性评价研究[J]. 环境科学与管理, 2007,32(9)：159-162.

[22] Sun T, Zhang H W, Wang Y, et al. The application of environmental Gini coefficient (EGC) in allocating wastewater discharge permit： The case study of watershed total mass control in Tianjin, China [J]. Resources, Conservation and Recycling, 2010,4(9)：601-608.

[23] 姜 雪,卢文喜,张 蕾,等.基于 WASP模型的东辽河水质模拟研究 [J]. 中国农村水利水电, 2011,(12)：26-30.

[24] Firdes Y, Aysegul A. Comparison of phosphorus reduction alternatives in control of nutrient concentrations in Lake Uluabat (Bursa, Turkey)： Partial versus full sediment dredging [J]. Limnologica, 2013,43(1)：1-9.

[25] Lin C E, Chen C T, Kao C M, et al. Development of the sediment and water quality management strategies for the Salt-water River, Taiwan [J]. Marine Pollution Bulletin, 2011,63(5—12)：528-534.

[26] 史铁锤,王飞儿,方晓波.基于水质分析模拟程序的湖州市环太湖河网区水质管理模式 [J]. 环境科学学报, 2010, 30(3)：631-640.

[27] Lindenschmidt K E, Fleischbein K, Baborowski M. Structural uncertainty in a river water quality modelling system [J]. Ecological Modelling, 2007,204(3/4)：289-300.

[28] 乔 飞,孟 伟,郑丙辉,等.长江流域污染负荷核算及来源分析[J]. 环境科学研究, 2013,26(1)：80-87.

[29] Wool T A, Ambrose R B, Martin J L, et al. Water Quality Analysis Simulation Program (WASP) Version 6.0DRAFT： User’s Manual [M]. Georgia： USEPA Environmental Research Laboratory, 2006.

[30] Bowie G L, Mills W B, Porcella D B, et al. Rates, constants, and kinetics formulations in surface water quality modeling [M] 2ndEdition. Georgia： USEPA Environmental Research Laboratory, 1985.

[31] Willmott C J, Ackleson S G, Davis R E, et al. Statistics for the evaluation and comparison of models [J]. Journal of Geophysical research, 1985,90(C5)：8995-9005.

[32] 杨松彬,董志勇.河网概化密度对平原河网水动力模型的影响研究 [J]. 浙江工业大学学报, 2007,35(5)：567-570.

[33] Dilks D W, Freedman P L. Improved consideration of the margin of safety in total maximum daily load development [J]. Journal of Environmental Engineering, 2004,130(6)：690-694.

Use of a minimum environmental Gini Coefficient model on optimizing the allocation plan of total pollutant load in water bodies： a case study at Zhangjiagang river-network plain.

TIAN Ping1,3, FANG Xiao-bo2*, WANG Fei-er1, ZHU Yao1
(1. College of Environmental and Resource Sciences, Zhejiang University, Hangzhou 310012, China；2. School of Environmental and Resource Sciences, Zhejiang Agricultural and Forestry University, Lin’an 311300, China；3. Zhejiang Zone-king Engineering and Technology Limited Company, Hangzhou 310004, China). China Environmental Science, 2014,34(3)：801～809

A Gini Coefficient model was developed in an attempt to optimize the total pollutants load allocation plan at the study area, Zhangjiagang river-net plain, where the environmental capacity of target pollutants and spatial distribution at six different towns in this region have been well addressed via WASP model. The local social, economic and resource factors were integrated and processed in developing this Gini Coefficient model, by which the best solution to the allocation pollutant plan was successfully figured out. As a consequence, the COD Gini Coefficients were decreased by 15.1% and 8.5% while ammonia Gini Coefficients were decreased by 11.0% and 13.7% in terms of pollutant discharge and capacity allocation respectively. The largest reduction rate of COD,approximately 20%,was achieved at Changjing town by the optimized load reduction strategy with an annual reduction, of 231.74tonnes. As to the ammonia pollutant load reduction, Zhutang Town showed the largest reduction rate of 59.9% with an annual reduction amount of 59.74tonnes.

Gini coefficient；minimum；total pollutant load allocation；environmental capacity；WASP model

X196;X52

：A

：1000-6923(2014)03-0801-09

田 平(1980-),男,浙江湖州人,工程师,博士,主要从事环境规划与管理研究.发表论文11篇.

2013-07-10

国家水体污染控制与治理科技重大专项课题(2008ZX07101-006);江阴市张家港河河道综合整治规划项目;浙江省教育厅项目(Y201120673);浙江农林大学发展基金预研项目(2010FK042);浙江农林大学人才启动项目

* 责任作者, 讲师, xbfang487@gmail.com