卫星遥感监测近地表细颗粒物多元回归方法研究

贾松林,苏 林,陶金花,王子峰,陈良富,尚华哲

(1.中国科学院遥感与数字地球研究所,遥感科学国家重点实验室,北京 100101；2.中国科学院大学,北京 100049)

卫星遥感监测近地表细颗粒物多元回归方法研究

贾松林1,2,苏 林1*,陶金花1,王子峰1,陈良富1,尚华哲1,2

(1.中国科学院遥感与数字地球研究所,遥感科学国家重点实验室,北京 100101；2.中国科学院大学,北京 100049)

对地基监测PM2.5和气象数据、MODISAOD卫星数据与NCEP FNL数据进行了处理分析,在与一元简单线性模型(模型1)进行对比的基础上,建立了适应于北京及其附近地区遥感监测近地面颗粒物(PM2.5)浓度的多元线性(模型 2)和非线性(模型 3)回归模型,并对模型进行了评价验证和遥感监测初步应用.结果表明：模型1,2,3分别能够解释PM2.532.5%,56.1%,62.7%的变异.反演的PM2.5浓度与站点监测值相关性分别为 0.5488(R2=0.3012), 0.7449(R2=0.5549), 0.7431(R2=0.5523).对于站点监测 PM2.5浓度 63.1652μg/m3的均值,反演均方根误差RMSE分别为43.5562, 35.3321, 36.8450μg/m3.模型2和3中气象因子分别能够解释PM2.523.6%和12.6%的变异,说明了气象因子影响北京地区春季PM2.5-AOD关系的显著性.3种模型整体上都不同程度地存在着低值高估和高值低估的现象.

近地表细颗粒物浓度(PM2.5)；卫星遥感监测；多元回归模型；气象要素；气溶胶光学厚度(AOD)

随着我国大气污染形势的日益严峻,特别是京津冀、长江三角洲、珠江三角洲等重点城市群出现了严重的复合型污染.遥感监测具有空间连续、探测范围大、受地面条件限制少、能在不同尺度上反映污染物的宏观分布和传输路径等优势,从而能为全方位立体监测大气污染提供重要的信息来源.近年来,各国学者对基于卫星遥感估算近地面颗粒物浓度和监测区域污染进行了广泛的研究,主要的思路都是直接或间接地借助其他参数建立气溶胶光学厚度 AOD(Aerosol Optical Depth)与近地面颗粒物浓度间的相关模型.Chu等[1],Slater等[2]将地基观测AOD与近地面PM10和PM2.5浓度进行了初步的相关分析,证明了由 AOD估算近地面颗粒物浓度的可行性. Wang等[3]、Koelemeijer等[4]、Engle-Cox等[5]、李成才等[6]、Guo等[7]直接将卫星遥感的 AOD与近地面颗粒物浓度进行相关比对,取得了较好的效果.Wang等[8]、Tao等[9]、Donkelaar等[10]将气溶胶垂直分布和相对湿度影响引入 PM2.5-AOD简单相关模型,经过垂直和湿度订正,有效减少了AOD和近地面颗粒物浓度间的不确定性.由于近地面颗粒物浓度与局地环境气候条件、地表类型、季节、污染状况有关,Gupta[11]、Pelletier等[12]、Liu等[13]、Tian等[14]进一步将上述各种环境气候因子引入AOD与近地面细颗粒物浓度间的相关模型中,以提高二者的相关水平.

本文将边界层高度、对流层底部相对湿度廓线均值、近地表相对湿度、近地表气温等气象因子引入到 PM2.5-AOD简单相关模型中,探索建立了适应于北京及其附近地区遥感监测近地面颗粒物浓度的多元线性和非线性回归模型,考察了气象要素对北京地区 PM2.5-AOD关系的影响,对比了两种多元回归方法反演 PM2.5的效果.

1 数据及其处理

1.1 地基PM2.5质量浓度数据

图1 北京地区PM2.5监测站点分布Fig.1 Distribution of PM2.5monitoring sites in Beijing

选择北京市环境保护监测中心向公众实时发布的北京地区35个站点的空气质量数据,对这些发布的数据进行了及时的跟踪记录并提取了PM2.5数据用于分析处理.

1.2 MODIS AOD卫星数据

美国国家航空航天局NASA的中分辨率成像光谱仪MODIS具有多光谱、宽覆盖和分辨率高等特点,搭载在TERRA和AQUA两颗卫星上,广泛用于大气气溶胶监测.NASA每日发布的二级气溶胶产品分辨率为星下点 10km,陆地 AOD波长在0.47,0.55,0.66μm,反演方法有暗像元算法和深蓝算法.本文下载了 2013年 1～4月下午星AQUA 的MODIS气溶胶产品,然后将暗像元算法和深蓝算法波长为0.55μm的AOD进行了融合提取以用于本研究.

1.3 地基气象数据

根据中国气象科学数据共享服务网向公众实时发布的北京地区28个气象站点观测的气象数据,对这些数据及时地跟踪记录并提取了气温和近地表相对湿度用于本研究的分析处理.

1.4 NCEP FNL全球分析数据

美国国家环境预报中心(NCEP)/美国国家大气研究中心(NCAR)为广大科研工作者提供了FNL 全球分析资料(Final Operational Global Analysis,以下简称为“FNL资料”).FNL资料空间分辨率为 1.0°×1.0°,时间分辨率为 6h.本文下载了20013年1～4月的FNL资料数据并提取了其中的边界层高度数据和对流层底部 7层(1× 105,9.75×104,9.50×104,9.25×104,9×104,8.50×104,8× 104Pa)大约2km以下相对湿度廓线数据并加以平均以用于本研究的分析.

所介绍的数据源中提取的数据总结如表1示.

1.5 数据处理与匹配

本文对上述数据进行了处理和匹配以便于建模、验证和分析,数据匹配的原则是空间上以PM2.5监测站点为准,时间上以卫星过境时间为准.

空间上∶地基气象数据与 PM2.5站点的匹配采用就近匹配.MODIS AOD则采用以PM2.5站点为中心 15km为半径的非零象元的均值.对于FNL资料的处理则是对离PM站点较近的4个格点进行反距离权重插值以作为该站点的 FNL资料数据.时间上∶由于采用 MODIS下午星AQUA(过境时间约为13∶30)的AOD数据,所以地基PM2.5数据和气象数据采用13∶00～14∶00点值的平均,FNL资料采用 UTC-6∶00(北京时间14∶00)的数据.

表1 本文研究用数据变量信息Table 1 Information of data variables in this paper

结果 PM 站点与气象站点匹配上的共有站点26个.本文将这些站点随机分成了建模站点和验证站点两部分,其中建模站点 18个,验证站点有8个占匹配站点总数的约1/3.经匹配的后的样点数据共 996例,其中建模站点样点例数为 663例,验证样点例数为332例,时间在2013年1月24日～4月29日.

2 模型方法与建模分析

2.1 方法介绍

本文拟探索建立适应于北京及其附近地区遥感监测近地面颗粒物浓度的多元线性和非线性回归模型,考察气象要素对北京地区 PM2.5-AOD关系的影响,对比两种多元回归方法反演PM2.5的效果.为便于对比分析,也建立了仅考虑PM2.5-AOD简单线性关系的模型.

模型1即仅考虑PM2.5-AOD简单线性关系的模型形式为∶

模型 2即考虑了气象要素的多元线性回归模型形式为∶

模型 3即基于一定物理意义的形式上为幂指函数的多元回归模型形式为∶

经对数变换后,其形式为∶

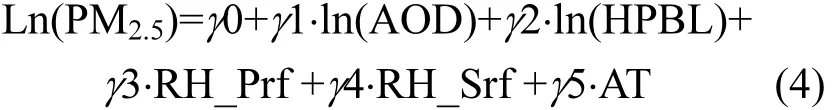
式(1)～(4)中,PM2.5是指地基监测的近地表PM2.5质量浓度小时均值(μg/m3);AOD是指波长0.55μm处的MODIS气溶胶光学厚度值(无单位); HPBL是指 FNL资料提取的边界层高度(km); RH_Prf为 FNL资料提取的对流层底部 7层(1×105～8×104Pa)约 2km之下的相对湿度的平均值(%);RH_Srf为地基测量的近地表相对湿度(%);AT为地基测量的近地表气温(℃);α0、α1、β0、β1、β2、β3、β4、β5、γ0、γ1、γ2、γ3、γ4、γ5为各模型中相应参数的回归系数.

模型 2和 3中各气象因子的加入是由PM2.5-AOD之间的相关关系理论决定的.地基监测近地表颗粒物浓度的测量在较为干燥的空气状态(相对湿度≤40%)进行,其公式为∶

PMχ为近地表空气动力学粒径小于等于X的颗粒物质量浓度,n(r,0)为近地表气溶胶粒子谱分布函数,ρ为近地表颗粒物密度.边界层内的气溶胶光学厚度(AOD(H))的公式可表达为∶

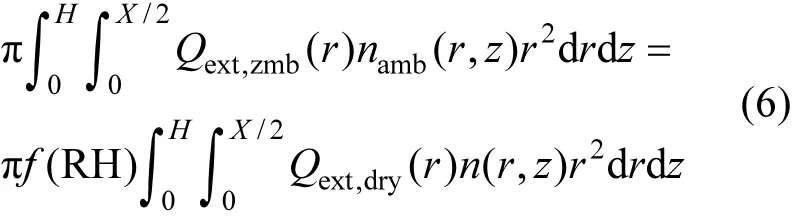
式中∶H为边界层高度;Qext,amb为环境状况下消光效率;namb(r,z)为环境状况下高度z处的颗粒物谱分布函数;Qext,dry为干燥状况下消光效率;ndry(r,z)为干燥状况下高度 z处的颗粒物谱分布函数;f(RH)是边界层内相对湿度廓线的函数,是对边界层内相对湿度廓线对颗粒物谱分布和消光效率影响的描述.根据 Hansen等[15]研究成果,定义归一化颗粒物消光效率()和有效半径(reff)两个参数∶

假定边界层高度内对流混合作用充分进行并且对流层之上颗粒物的垂直分布是相对平滑的,那么边界层高度内气溶胶粒子的属性(谱分布n(r)、密度ρ等)在不同高度的分布将趋于均一.这个假定在白天陆地上有充分的表面加热时尤其成立[16].机载和地基测量也表明了大气柱内颗粒物大部分存留在较低的对流层内,并且由于垂直混合的作用边界层内的颗粒物质量分布较均一[17].根据公式(5-8)和上述假定可推得∶

根据上述假定还可得出边界层内气溶胶光学厚度(AOD(H))占了整个大气柱气溶胶光学厚度(AOD)的大部分,设AOD(H)与AOD的比值为α,进而得∶

于是便可得出经边界层高度(H)和边界层内相对湿度廓线订正(f(RH))订正的气溶胶光学厚度AOD*=AOD/[H⋅f(RH)]将与近地表颗粒物浓度有更好的相关性.Koelemeijer等[4]在研究欧洲地区MODIS AOD与PM的时空变化特征对比时发现了这一点并进行了类似的理论推导.模型2和3中HPBL和RH_Srf的加入正是基于上述PM2.5-AOD相关关系理论的考虑.颗粒物的组成、谱分布以及垂直廓线是影响近地表PM2.5浓度和AOD关系的关键性因子[13],模型2和3中加入的近地表相对湿度RH_Suf和气温AT则被视为影响这些关键因子的区域敏感性因子.

2.2 建模数据统计特征描述

对1.5中处理和匹配后的663例建模数据统计特征进行了简要的描述和分析,表2是建模数据中各参数的统计特征描述参量,图2是建模数据中各参数的频率分布直方图.

表2 建模数据中各参数的统计特征描述Table 2 Description of statistical characteristic of all variables in modeling data

PM2.5和AOD的频率分布直方图具有相似性,可初步判定PM2.5与AOD之间存在着一定的相关性.PM2.5的最小值为 3μg/m3,最大值为 196μg/m3,均值为62.2775μg/m3,这表明了北京地区春季较高的PM2.5背景值.RH_Prf的最小值是12.67%,最大值为 64.69%,均值为 29.94%.RH_Srf的最小值是7.00%,最大值为63.00%,均值为23.91%,这表明了北京地区春季较为干燥的气候特征.

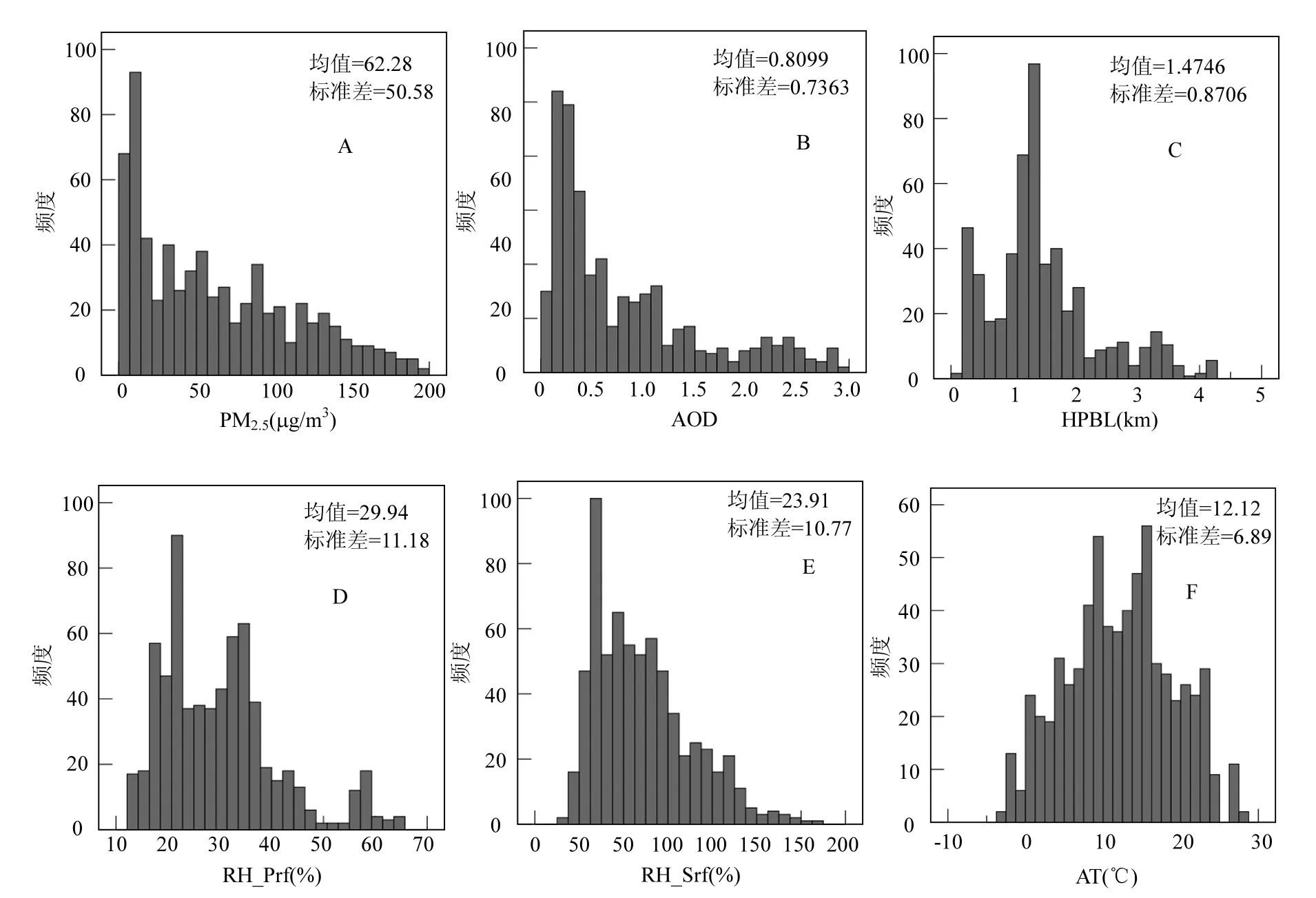
图2 建模数据中各参数的频率分布(N=663)Fig.2 Frequency distribution histogram of all variables in modeling data (N=663)

2.3 建模结果与分析

将2.2中描述的建模数据分别应用于2.1中所介绍的模型1,2,3并进行回归分析得到3种模型的回归系数如表3,表4和表5所示.

表3 模型1回归系数(N=663,R2=0.325,P<0.001)Table 3 Regression coefficients of Model1 (N=663,R2=0.325,P<0.001)

从总体上来看,对3个模型进行方差分析的P值都小于0.001,说明了3个模型整体的合理性和模型中各影响因子整体上对 PM2.5变异影响的显著性.相比于模型1能够解释PM2.532.5%的变异(R2=0.325),模型2能够解释 PM2.556.1%的变异(R2=0.561),提高了72.62%,也说明了气象因子(HPBL、RH_Prf、RH_Srf、AT)在模型2中解释了PM2.523.6%的变异.相对于PM2.5的地表监测均值 66.2275µg/m3,模型 1的均方根误差RMSE为 41.5310µg/m3,模型 2的 RMSE为 34.6079µg/m3,比模型1降低了16.67%.从模型1和 2整体指标的对比可以看出模型 2在预测PM2.5的优异性,也说明了气象因子(HPBL、RH_Prf、RH_Srf、AT)综合影响PM-AOD关系的显著性.

表4和表5中显示模型2,3回归分析中对各影响因子(AOD、HPBL、RH_Prf、RH_Srf、AT)进行T检验的p值都小于等于0.001,表明了这些因子分别对PM2.5影响的显著性.

模型 3能够解释 ln(PM2.5)62.7%的变异(R2=0.627),逐步回归显示 AOD 能够解释ln(PM2.5)50.1%的变异,气象因子能够解释ln(PM2.5)12.6%的变异.相对于地表监测ln(PM2.5)的均值3.6442,拟合ln(PM2.5)的均值为3.6321、RMSE为 0.6958,经过对数变换反变换即指数变换后,相对于地表监测 PM2.5的均值 66.2275µg/ m3,预测PM2.5的均值为55.5879µg/m3, RMSE为37.0082µg/m3.

表4 模型2回归系数(N=663,R2=0.561,P<0.001)Table 4 Regression coefficients of Model2 (N=663,R2=0.561,P<0.001)

表5 模型3回归系数(N=663,R2=0.627,P<0.001)Table 5 Regression coefficients of Model3 (N=663,R2=0.627,P<0.001)

3 验证

将2.3中建立的模型1,2,3分别应用于验证数据,并与地基观测的 PM2.5浓度进行比对,结果见图3和图4.

将模型1,2,3分别应用于验证数据,产生的回归方程的斜率分别是 0.3041,0.5928,0.6902,截距分别是 43.695,31.866,12.811;反演值和观测值的相关系数R分别是0.5488(R2=0.3012),0.7449(R2= 0.5549),0.7431(R2=0.5523);对 于 平 均 值 为64.0316µg/m3的 PM2.5观测值,3种模型反演的PM2.5均值分别为64.0316,69.8211,57.0073µg/m3,均方根误差 RMSE分别为 43.5562,35.3321, 36.8450µg/m3.

图3 模型1、2、3反演PM2.5质量浓度与近地表监测PM2.5质量浓度散点图(A,B,C,N=332)Fig.3 Scatter plots of the model 1,2,3estimated PM2.5concentration vs. the observed PM2.5concentration (A,B,C,N=332)

从斜率和截距来看,3种模型的斜率均小于1,截距均大于 0,说明都存在这一定程度的低值高估和高值低估的现象,模型1尤为明显,如图4所示.与模型 1相比较,模型 2的斜率提高了94.94%,截距降低了 27.87%,有效缓解了低值高估和高值低估的现象,如图4所示;模型3的斜率提高了126.96%,截距降低了70.68%,进一步缓解了低值高估和高值低估的现象,尤其是在 PM2.5观测值的低值区,模型 3的低值高估现象的缓解作用更为显著,反演效果较好,如图4所示.

图4 模型1、2、3反演PM2.5质量浓度与近地表监测PM2.5质量浓度关系(N=332)Fig.4 Line chart of the model 1, 2, 3estimated PM2.5concentration vs. the observed PM2.5concentration (N=332)

从反演相关性、均方根误差这些整体表征反演精度的指标来看,与模型1相比,模型2,3的反演相关性分别提高了 35.73%,35.40%,反演均方根误差分别降低了 18.88%,15.40%.由此从独立数据验证的角度再次说明了气象要素(HPBL, RH_Prf, RH_Srf, AT)对PM2.5-AOD关系影响的显著性,是在近地面 PM2.5浓度卫星反演中必须考虑的重要因子.

4 模型实现与遥感监测初步应用

以2013年3月27日为例,本文将3个模型应用在了卫星遥感监测京津冀地区细颗粒物(PM2.5)质量浓度的监测实践中.首先下载了NASA下午星AQUA的AOD产品,并对因云覆盖而无值的区域进行了反距离权重插值处理,如图5(A)示,然后将NCEP FNL全球分析数据中的相关气象数据内插到AOD产品相应的网格中,最后将2.3中建立的3个模型分别应用于NASA AOD产品数据和FNL资料相关气象数据,从而得到了2013年3月27日京津冀地区细颗粒物(PM2.5)质量浓度的遥感监测图,如图5示.

由图5中可见,3个模型遥感监测的细颗粒物(PM2.5)质量浓度整体上分布具有一致性,且与AOD的分布也呈现出整体的一致性∶高值主要分布在区域的东东南南部,低值主要分布在区域的西北北部.区域的西北部为太行山北缘,北部为燕山山脉,人为污染源较少,所以区域的西北北部地区细颗粒物(PM2.5)质量浓度分布较低;而区域的东中南部属华北平原,又处于京津唐经济发展带,人为颗粒物污染源(日常发电、工业生成、汽车尾气排放等)较多,所以区域东东南南部地区细颗粒物(PM2.5)质量浓度分布较高.

部分3的验证分析中已指出,模型1存在着明显的低值高估和高值低估的现象,如图5(B)示,模型2和3有效地改善了这个问题,如图5(C、D)示,尤其是模型3在低值区反演效果较好,如图5(D)所示区域西北部.在高值区,模型2和模型3也都能进行较好的反演,如图5(C、D)所示区域东南部.

图5 2013年3月27日京津冀地区NASA AQUA AOD与模型1,2,3遥感监测PM2.5浓度分布Fig.5 Distribution of NASA AQUA AOD and the model 1, 2, 3estimated PM2.5concentrationin Beijing-Tianjin-Hebei region on Mar. 27, 2013

5 结论

5.1 从建模的结果来看,模型 1,2,3分别能够解释PM2.532.5%,56.1%,62.7%的变异.

5.2 在用独立数据进行验证中,模型 1,2,3反演的PM2.5浓度与站点监测值相关性分别为0.5488(R2=0.3012),0.7449(R2=0.5549),0.7431(R2=0.5523 );对于站点监测PM2.5浓度63.1652µg/m3的均值,反演均方根误差RMSE分别为43.5562, 35.3321, 36.8450µg/m3.

5.3 说明了气象因子(边界层高度HPBL、对流层底部相对湿度廓线均值 RH_Prf、近地表相对湿度 RH_Srf、近地表气温 AT)影响北京地区春季PM2.5-AOD关系的显著性,模型2和3中气象要素分别能够解释PM2.523.6%和12.6%的变异,因而气象要素是在近地面PM2.5浓度卫星反演中必须考虑的重要因子.

5.4 3种模型整体上都不同程度上存在着低值高估和高值低估的现象∶模型1问题较明显,模型2问题得到较大的改善,模型 3问题也得到较大的改善,尤其是在低值区反演效果较好,但高值区反演偏差波动性较大.

5.5 将3个模型初步应用在了京津冀地区PM2.5质量浓度的遥感监测实践中,相比于模型 1,模型2和模型3取得了较好的效果.

[1] ChuD A, Kaufman Y J, Zibordi G, et al. Global monitoring of air pollution over land from the Earth Observing System-Terra Moderate Resolution Imaging Spectroradiometer (MODIS) [J]. Journal of Geophysics Research, 2013,108(D21)：1-18.

[2] Slater J F, Dibb J E, Campbell J W, et al. Physical and chemical properties of surface and column aerosols at a rural New England site during MODIS overpass [J]. Remote Sensing Environment, 2004,92：173-180.

[3] Wang J, Christopher A. Inter-comparison between satellitederived aerosol optical thickness and PM2.5mass： Implications for air quality studies [J]. Geophysics Research Letters, 2003,30：1-4.

[4] Koelemeijer R B, Homan C D, Matthijsen J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over Europe [J]. Atmospheric Environment, 2006,40：5304-5315.

[5] Engle-Cox J A, Holloman C H, Coutant B W. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality [J]. Atmospheric Environment, 2004,38：2495-2509.

[6] Li C C, Mao J T, LauA K, et al. Application of MODIS aerosol product in the study of air pollution in Beijing [J]. Science in China — Ser. D Earth Science, 2005,35：177-186.

[7] Guo J, Zhang X, Che H, et al. Correlation between P M concentrations and aerosol optical depth in eastern China [J]. Atmospheric Environment, 2009,43：5876-5886.

[8] Wang Z F, Chen L F, Tao J H, et al. Satellite-based estimation of regional particulate matter (PM) in Beijing using vertical-and-RHcorrecting method [J]. Remote Sensing of Environment, 2010,114(1)：50-63.

[9] Tao J H, Zhang M G, Chen L F, et al. Method to estimate concentration of surface-level particulate matter from satellite-based aerosol optical thick-ness [J]. Sci. China Earth Sci., 2013,43(1)：143-154.

[10] Donkelaar A V, Martin R V, Park R J. Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing [J]. Journal of Geophysics Research, 2006, D21201,111：1-10.

[11] Gupta P, Christopher S A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products： Multiple regression approach [J], J. Geophys. Res., 2009,114(D14)：1-13.

[12] Pelletier B, Sater R, Vidot J. Retrieving of particulate matter from optical measurement： A semi-parametric approach [J]. Journal of Geophysics Research, 2007,112：1-18.

[13] Liu Y, Sarnat J A, Kilaru V, et al. Estimating ground-level PM2.5 in the eastern United States using satellite remote sensing [J]. Environmental Science and Technology, 2005,39：3269−3278.

[14] Tian J, Chen D, A semi-empirical model for predicting hourly ground-levelfine particulate matter (PM2.5) concentration in southern Ontario from satellite remote sensingand ground-based meteorological measurements [J]. Remote Sensing of Environment, 2010,114：221-229.

[15] Hansen J E, Travis L D. Light scattering in planetaryatmospheres [J]. Space Science Reviews, 1974,16：527—610.

[16] Holton J R. An introduction to dynamic meteorology [M]. London： Elsevier Academic Press, 2004.

[17] Clarke A, PorterJ, Valero F, et al. Vertical profiles, aerosol microphysics, and optical closure during the Atlantic Stratocumulus Transition Experiment： Measured and modeledcolumn optical properties [J]. J. Geophys. Res., 1996,101：4443-4453.

致谢：感谢陈兵老师和余超老师对论文中英语部分的修改.

A study of multiple regression method for estimating concentration of fine particulate matter using satellite remote sensing.

JIA Song-lin1,2, SU Lin1*, TAO Jin-hua1, WANG Zi-feng1, CHEN Liang-fu1, SHANG Hua-zhe1,2
(1.State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China；2.Graduate University of Chinese Academy of Sciences, Beijing 100049, China). China Environmental Science, 2014,34(3)：565～573

In comparison with the simple linear model (Model 1), we developed two multiple regression modelslinearmodel (Model 2) and nonlinear model (Model 3)-to estimate the ground PM2.5concentration using satellite observationsover Beijing and its surrounding area based on the analysis of the PM2.5data, the meteorological data, the MODIS AOD dataand the NCEP FNL data. Results showed that Model 1, Model 2 and Model 3 could explain 32.5%, 56.1%, 62.7% of the variability in ground-level PM2.5concentration respectively. Correlation coefficients (R) of the three model estimated values of PM2.5mass concentration with the actual observations were 0.5488, 0.7449, 0.7431 respectively. With an average PM2.5concentration of 63.1652 µg/m3, their RMSEs were 43.5562, 35.3321,36.8450µg/m3respectively. Meteorological factors in Model 2 and Model 3 could separatelyexplain 23.6%, 12.6% of the variability in ground-level PM2.5concentration, which indicatedtheir significant influenceson the PM2.5-AOD relationship. In addition, there were low-value overestimation and high-value underestimation phenomenon in the three models.

concentration of fine particulate matter (PM2.5)；satellite remote sensing；multiple regression method；meteorological factors；aerosol optical depth (AOD)

X87

：A

：1000-6923(2014)03-0565-09

贾松林(1990-),男,河南商丘人,中国科学院遥感与数字地球研究所硕士研究生,主要从事大气遥感方面的研究工作.

2013-06-28

国家“973”项目(2010CB950801);中国科学院战略性先导科技专项资助项目(XDB05020100)

* 责任作者, 研究员, sulin@irsa.ac.cn