基于神经网络验证压电方程的正确性

葛振庭 施伟辰

(上海海事大学 物流工程学院，中国 上海201404)

0 研究背景

材料从使用性能上可以分为结构材料和功能材料两大类[1]，其中结构材料以其强度、韧性、硬度、弹性等力学特性为 应用依据，功能材料以其电、磁、光、声、热等物理性能为基础，用以制作有特殊功能的器件。压电材料是实现机械能与电能相互转换的功能材料[2]，是一类对机、电、声、光、热敏感的电子材料，外力和电场之间的耦合为压电材料提供了一种机制，用于感测力学载荷所诱发电位变化，并通过外部电场改变结构应。压电材料的结构可靠性已引起越来越多的关注，因为它们大多是被应用在微机电系统中,而微机电系统的大量应用也决定了研究压电材料的重要意义。

1 压电材料的本构方程

在线性压电材料的情况下,我们可以构建横向的等方性压电材料的六角形晶体模型,从而得出以下本构方程组[3]：

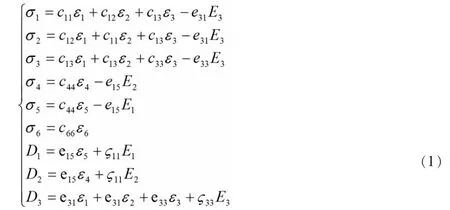
其中σ表示应力大小,ε表示应变大小,E表示电场强度大小，D表示电位移的大小，c与ζ为此本构方程的常系数，下标1，2，3表示空间坐标系中的三个方向，坐标系表示分别为x1，x2，x3。以下关系式（2）说明了方程（1）中具体应力应变的方向及含义：

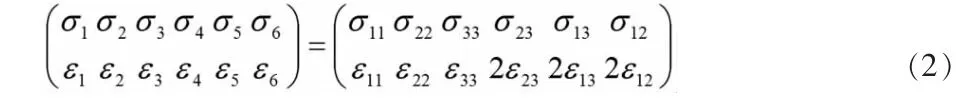
2 神经网络

人工神经网络(简称神经网络)是由人工神经元互连组成 的网络，是一种非线性动力学系统，它采用类似于“黑箱”的方法，通过学习和记忆而不是假设，找出输入、输出变量之间的非线性关系（映射），在执行问题和求解的时候，将所获取的数据输入给训练好的网络，依据网络学习的知识进行网络推理，得出合理的答案与结果。其中BP神经网络是目前发展比较成熟的一种人工神经网络，约有80%的神经网络系统采用BP网络。它是一种反馈式全连接多层神经网络，具有结构简单，工作状态稳定等优点，并且具有较强的联想、记忆和推广能力，可以以任意精度逼近任何非线性连接函数[4]。

3 压电陶瓷平面方程验证

本文将针对PZT-4压电陶瓷的本构方程进行研究。对于此种压电材料，本构方程里面的常系数c与ζ均为已知常数。此压电材料属于线性压电材料的范畴，为减少数据量的运算，方便神经网络的预测，本文将着重针对该材料的二维平面方程进行验证。对于平面问题，不妨设坐标x2方向上的应力大小为0，则根据弹性力学中平面应力基本模型，此时可知坐标系x2方向上的电位移D2=0，且凡是下标带有x2的应力与应变大小均为0。故可以得出以下关系式（3）。

故根据式（1）（2）（3）可得 x1，x3的平面本构方程如下：

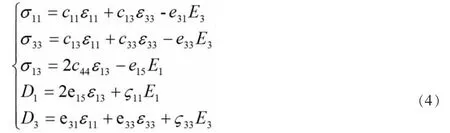
其中常系数的含义及数值单位如右所示：弹性常数：c（1010N/m2），压电常数 e（10C/m2），ζ（10-9C/Vm），具体数值见式（5）：

根据式（3）（4）（5）分别给应变 ε11ε13ε33以及电场强度 E1E3这五个量赋值，将输入值带入方程（4）从而得到应力电位移σ11σ33σ13D1D3这五个输出值。从而再将输入值ε11ε13ε33E1E3作为训练神经网络的输入样本，由于此方程的准确系数已经根据实验测出，故输出值可以认做是准确数据，将此处的输出值σ11σ33σ13D1D3作为训练神经网络的输出样本。考虑到神经网络对输入数据区别的要求，此处带入的输入样本值均将小于1，省去了输入前归一化的步骤，即此处输入数据可以直接当做样本数据来使用。为了保证网络的训练精度，在此使用9组样本数据进行神经网络训练，见下表1。每列从上到下的数据分别为 ε11ε13ε33单位为：10-5，E1E3单位为：10-5N/C，σ11σ33σ13单位为：10-5N/m2,D1D3单位为：10-5C/m2。

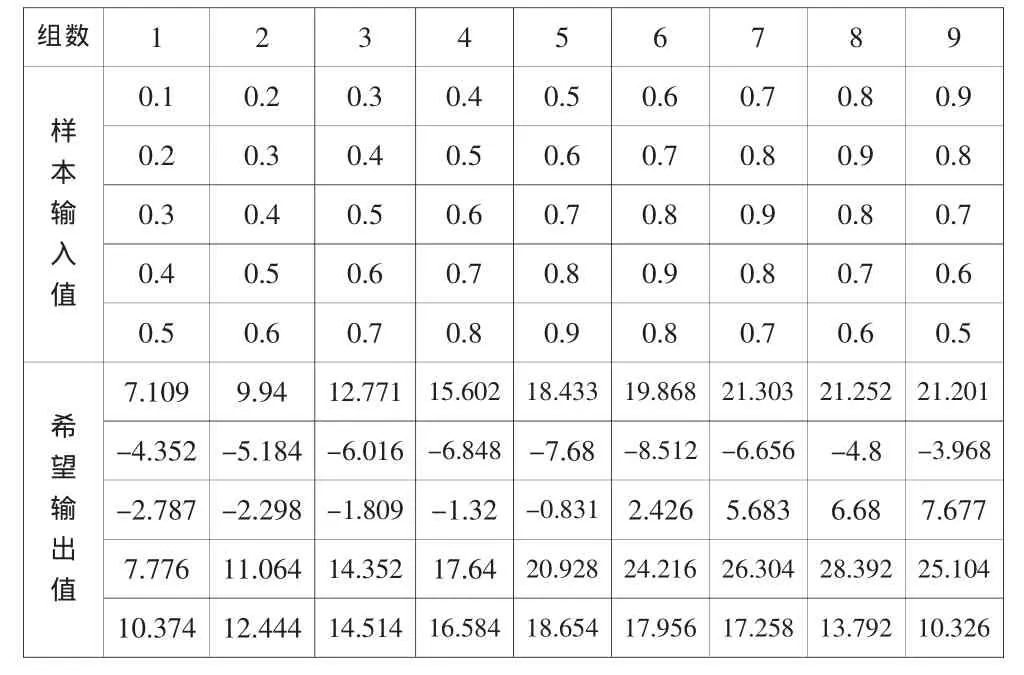
表1 训练神经网络样本输入输出数据

利用Matlab里内置的神经网络工具，在了解了BP网络的工作原理后，建立具体网络模型。此例中输入层有5个节点，分别是ε11ε13ε33E1E3这五个输入值,隐含层设置了9个节点,输出层有5个节点,即识别方程的输出值σ11σ33σ13D1D3。本例中应用了logsig训练函数，且表1中的样本数据差异大，可以直接用Matlab进行训练，经过10000次训练后网络的目标函数精度为1.337×10-10，迭代过程见下图1。

为了验证方程的准确性，任选一组ε11ε13ε33E1E3作为输入数据，分别为 0.1,0.2,0.4,0.5,0.7;将其带入到方程（4）中，则可以得到一 σ11σ33σ13D1D3数据分别为：9.248，-5.696，-4.425，8.376，14.526 此组数据为真实的输出数据。再将这组输入数据带入已训练好的神经网络，从而得 出 网 络 的 预 测 输 出 值 分 别 为 9.2594，-5.6982，-4.4196，8.3878，14.5338。此处数据的单位均如上文所述。比较输出数据的值，将这两组输出数据分别作在同一坐标系内，见上右图2，其中实际值为红色六角星标注，预测值为黑色星号标注，发现实际值与预测值误差很小，可以说明该神经网络具有较高的预测精度，至此，运用神经网络的方法可以证明此压电本构方程线性

关系的准确性很高，即可验证此压电平面本构方程是正确的。

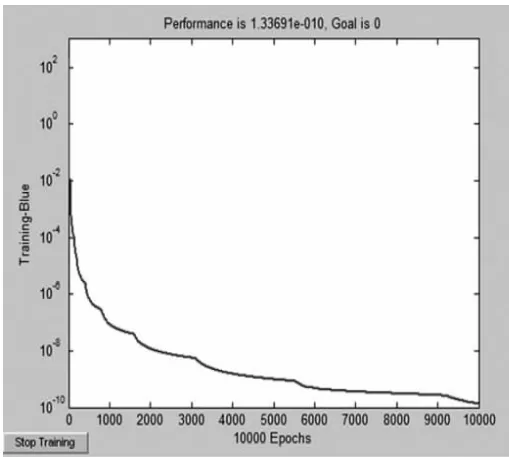
图1

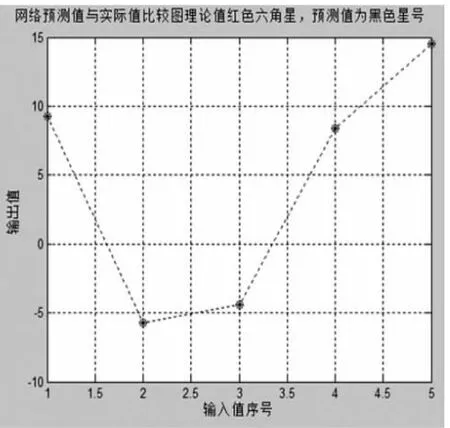
图2

4 结论

平面压电本构方程中的线性常数已经给出，通过输入多组输入数据根据本构方程得到准确的输出数据作为神经网络的样本训练数据，借由神经网络极强的模拟映射关系，训练好的网络可以预测出任意数据关系模型，包括此处的线性关系模型。本文通过神经网络验证压电方程中数据之间的线性关系，是一种很好的验证方法，具有一定的使用意义。

［1］盖学周.压电材料的研究发展方向和现状[J].中国陶瓷，2008，5（44）：9－13.

［2］裴先茹，高海荣.压电材料的研究和应用现状[D].郑州：郑州师范学院.

［3］Fuqian Yang.Department of Mechanical Engineering,University of Rochester,233 Hopeman Building,Rochester,NY 14627-0132,USA Received 13 October 1999;in revised form 21 May 2000[Z].

［4］贾艳春.人工神经网络应用于地下洞室围岩参数识别[J].模式识别与人工智能，1996，9（1）：71-77.