基于G-K模糊聚类的故障诊断方法研究
郑庆利
(中国人民解放军91604部队,山东 龙口 265700)
0 引言
近年来,随着故障诊断技术理论研究的不断深入,各种方法相互渗透借鉴,目前该领域我国在大系统故障诊断、多元统计分析、基于信息融合方法、基于神经网络的方法、基于专家系统方法等方面取得了一系列的研究成果,其中部分领域处于国际领先地位[1-2]。尽管故障诊断技术的相关研究不断深入,取得了很多成果,但工业技术的整体进步迅猛,使得故障诊断技术理论及应用研究都急需加强。目前该领域的研究热点问题有[3]:复杂系统多故障检测;基于人工智能的故障推理机制;多信息融合故障诊断方法;强扰动系统故障诊断;实用化工程故障诊断软件的开发。
聚类分析是近二十年发展起来的一种新的数学方法,聚类就是将一个数据集划分为若干组或类的过程并使同一组内的对象具有较高相似度,而不同组的对象之间相似度较差,组内对象之间的相似度越高而不同组对象之间的差别程度越大,聚类的质量也就越高。故障诊断领域应用最多的是基于模糊理论衍化的各种模糊聚类分析方法[4],因为对故障的识别问题往往伴有模糊性,即需要确定的不仅是定性的有或者无,更重要的是相识程度,这些问题用模糊语言来表达更为自然和符合实际。
1 模糊聚类故障诊断模型
Gustafson-Kessel(G-K)算法是距离自适应动态聚类算法的模糊推广,可以用于搜索椭圆型、平面和线型的数据模式的聚类。G-K算法在模糊模型的识别中对数据类的几何结构特征刻划要好于其他算法。
G-K算法中,定义vi为第i个原型类的中心,Mi为与第i个聚类中心的协方差矩阵Fi相关的正定对称矩阵,n为输入输出成绩空间的维数。则点xj到聚类Ci的距离可以定义为

设U=[uik]为待进行处理的数据集X{x1,x2…,xN}的模糊划分矩阵,则将X划分成c个模糊类别的最小化目标函数可以表示为

m∈(1,∞)为模糊指数,决定着所得分类的模糊程度(对于清晰模型,m=l;模糊模型m>1,大多数情况下取 m=2)。 Lagrange乘子 λk可以将上述目标函数及其约束转化成新的目标函数
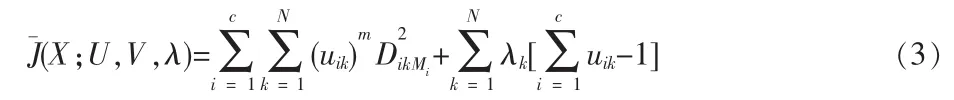

在某种程度上,第i类的形状可以用下述的散点矩阵来描述

如果数据集围绕中心点形成椭圆形聚类,那么椭圆的主轴将由Si的特征向量近似给出,而轴的相对长度等于其特征值。由于G-K算法使用了各模式类Ci的模糊协方差矩阵Fi的估计信息,而Fi的特征结构能够提供其相应模糊类Ci的形状和方向信息,因此G-K模糊聚类能够在同一个数据集中识别出不同形状和方向的模糊模式类,对数据集中的模式类原型具有一定的自适应性。
G-K算法可以表述如下[5]。
给定一组数据 X{xj|j=1,2,…,N},首先假定聚类中心为 vi,协方差矩阵为Fi,模糊划区矩阵为U=[uij],迭代执行以下步骤
1)计算距离

如果对某些 i=k,存在 d2(xj,Ci)=0,则令 ukj=1,而且∀i≠k,uij=0
3)计算新的聚类中心

使用G-K算法对数据集X进行聚类,实际上是对输入数据空间进行与数据集中的原型相适合的、随数据集的变化而精细可调的“软”划分,原来的数据集被分成了一组模糊类Ci(1≤i≤c),其聚类中心为vi(1≤i≤c),模糊划分矩阵为 U=[uik](1≤i≤c,1≤k≤N)。
2 基于G-K模糊聚类的故障诊断模型
当将G-K模糊聚类用于输入输出乘积空间的故障数据时,相应于不同质量的故障诊断模型,一些特有的聚类结果就产生出来。
假设x∈Rn是输入数据向量,y∈R是故障类别,即输出数据为整数。记Zk=[,yk]T,k表示第k个数据点,定义模糊聚类Ci的类型为相应聚类中心 Vi=[vi1,vi2,…,vi,n+1]T类型分量 vi,n+1。
命题1 高质量的故障诊断模型意味着每一个聚类具有很高的分类精度,这在聚类结果中直观地表现为类Ci的几乎所有的数据点的类别值是相等的,而且它们几乎等于聚类中心Vi=[vi1,vi2,…,vin]T的类型分量 vi,n+1,即 vi,n+1=yik。 这样聚类 Ci的模糊协方差矩阵 Fi具有下面的形式
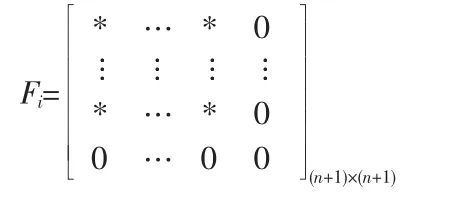
Fi的最后一行和最后一列对应着聚类Ci的类型。上式表明:
1)故障类别变量y与其它数据点的协方差近似为零,即cov(x,y)=0;
2)聚类Ci的故障类别变量夕的方差近似为零,即
D(vi,n+1)=cov(y,y)=Fi(n+1,n+1)≈0
那么,聚类Ci(1≤i≤c)的高斯隶属函数是一些窄脉冲,它们的中心等于聚类中心的类型分量vi,n+1,如下图1所示。

图1 高质量故障诊断模型类Ci中的类型vi,n+1隶属函数
命题2低质量的故障诊断模型意味着大部分聚类的分类精度是很低的,在聚类的结果中表现为大多数聚类Ci的数据点的类别值具有很大的差异,而且,它们远远偏离聚类中心Vi=[vi1,vi2,…,vin]T的类型分量 vi,n+1。 这 表 明:
1)故障类别变量y与其它数据点的协方差通常为非零值,即cov(x,y)>0;
2)聚类Ci的故障类别变量的方差是一大的数值,即,
D(vi,n+1)=cov(y,y)=Fi(n+1,n+1)>0
因此,相应于低质量的故障诊断模型,其聚类的高斯隶属函数具有一些平坦的
曲线,它们的中心偏离于它们真实的类别值,如图2所示。

图2 低质量故障诊断模型类Ci中的类型vi,n+1隶属函数
由此这样在乘积空间中使用G-K算法进行聚类后,我们实际上获得了一组模糊类Ci(i=1,2,…,C)在以上的模型中,对积空间中C个聚类中心的方差D(vn+1)设立了一个容差向量,tolSig2>0,∈RC,其中C是类数量。只有所有聚类中心的方差都满足
D(vi,n+1)<tolSig2(i)(i=1,2,…,C)
的聚类结果才被接受用来建立故障诊断模型;否则,增加聚类数目C,再一次执行模糊聚类算法。
3 G-K模糊聚类故障诊断方法
模糊聚类Ci在输入空间中可以用它的中心向量[vi1,vi2,…,vin]和方差向量[]来表征。如果对每一个聚类分量指定一个高斯型隶属函数
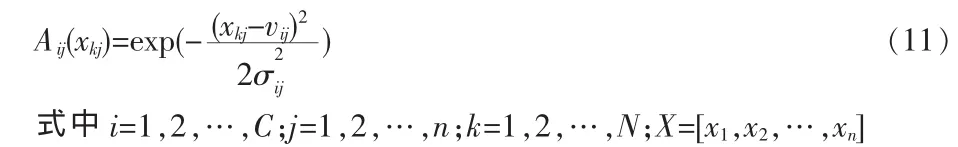
这些隶属函数可以通过将聚类Ci投射到它的每一维上获得,那么可以得到一组模糊故障诊断规则,规则中的每一个前件命题表示成单变量模糊集命题的逻辑组合,单变量模糊集是针对X的各个分量定义的,并且通常以下面逻辑与的形式给出
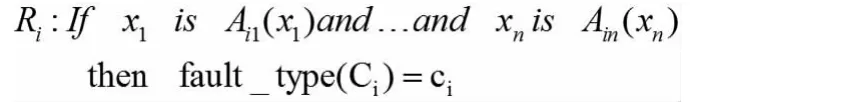
在这种情况下,数据xk相对于故障聚类Ci的故障度DoFi(xk)可被定义为投射空间中各隶属度的乘积

而在笛卡尔乘积空间中,DoFi(xk)可以被简单地定义为多维模糊集Ci的隶属度

总结以上可以得出以下结论:
对于任意数据 Data(i),如果{DoFj(Data(i))≥TH(j),(j=1,2,…,C)}(TH为预先定义的一个常数阀值向量),那么Data(i)∈Cj;否则Data(i)∉Cj。 通过 DoFj(Data(i))j=1,2,…,C,数据样本 Data(i)的最终类型综合为下面的两种情况:
1)存在一个或多个 DoFj(Data(i)),使
DoFj(Data(i))≥TH(j),j=1,2,…,C
这种情况下,如果所有聚类规则的后件值(即聚类中心的vi,n+1和分量)都相等或近似相等 那么取具有最大DoF(Data(i))值的聚类,j作为数据Data(i)所属的类;否则,数据Data(i)就被看成是无法识别的数据点。
2)不存在 DoFj(Data(i)),使得
DoFj(Data(i))≥TH(j),j=1,2,…,C
这意味着没有检测到故障,系统工作状态正常。
4 实例分析
采用某装置电源系统的故障诊断进行本文算法的仿真研究。表1为由故障仿真平台产生的测量数据集,共15组采样数据,最后一列是故障类型:1-能量衰减故障,2-线性分路电流控制器故障,3-无故障。

表1 电源系统故障诊断的数据集
对该数据集选择属性Icna和Icnb建立故障诊断模型,得到7个故障模式类,如表2所示。于是,根据表2,获得电源系统的故障诊断规则如下:
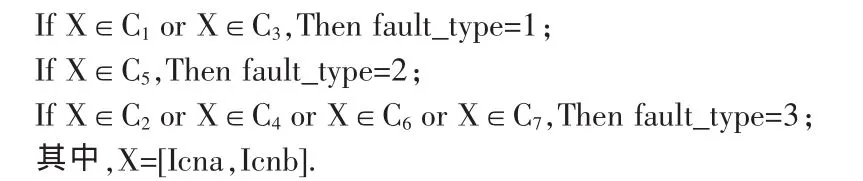
当设定tolV=0.01及tolSig2=0.01时,上述模糊故障诊断模型对训练数据表1的识别精度达到100%。由故障仿真平台另外产生15组数据样本作为测试数据集,所获得的故障诊断模型的有效识别精度可达93.3%,实验结果表明该方法是有效的。
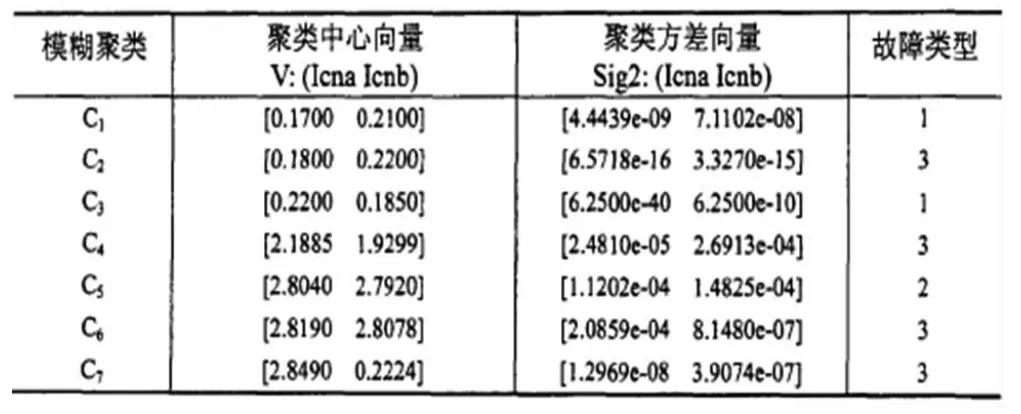
表2 用于故障诊断模型的模糊聚类
5 结束语
利用G-K算法提出了一种在输入输出乘积空间中,通过模糊聚类获得基于知识的故障诊断模型的方法。该方法可以发现数据集中不同形状和方向的故障模式,同时该方法比传统的故障诊断模型更具柔性,具有更强的处理噪声数据的能力。
[1]周东华.国内动态系统故障诊断技术的一些最新进展[J].自动化博览,2007(10):16-18.
[2]于春梅,杨胜波,陈馨.多元统计方法在故障诊断中的应用综述[J].计算机工程与应用,2007,43(8):205-208.
[3]BO-SUK YANG,XIAO DI,TIAN HAN,Random forests classifier for machine fault diagnosis[J].Journal of Mechanical Science and Technology,2013,22(9):16-25.
[4]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004:2-40.
[5]杜运成,石红瑞,杨晓波.控制系统故障诊断方法综述[J].工业仪表与自动化装置,2008(5):9-13.
[6]Lv Ning,Qiao Yu-jing,Yu Xiao-yang,et al.Building of fault diagnosis model based on Custafson-Kessel fuzzy clustering.Harbin Institute Technology Publishers[C]//Proceedings of the 3th International Symposium on Instrumentation Science and Technology,2004,1:511-516.

