改进EZW算法及其应用

赵双双

(金乡县人民医院，山东 金乡 272200)

改进EZW算法及其应用

赵双双

(金乡县人民医院，山东 金乡 272200)

数据压缩；小波变换；EZW算法；改进算法；EEG信号

近年来脑电图已广泛应用于脑疾病的诊断，对脑电现在一般是采取长时间监测，这就使得要存储或传输的数据量较大。因此，有必要对EEG信号压缩进行研究，并取得了一定进展[1-3]。数据压缩就是减少必须分配给指定消息集合或数据采样集合的信号空间的数值，数据压缩属于信源编码的范畴[4]。目前对脑电的压缩方法有矢量量化、多项式拟合、差分脉冲编码调制、小波变换编码等方法，其中小波变换在时域和频域具有良好的压缩特性，尤其适合于这种非平稳信号的数据分析和压缩，适用于生物医学信号的分析与处理[5]。Shapiro提出的嵌入式零树编码算法是一种较为成功的二维图像小波压缩算法[6]，本文在探讨小波变换和嵌入式零树小波算法的基础上，给出一种改进算的嵌入式零树小波算法，对改进算法进行分析并将其应用于一维EEG信号传输压缩中，以期对一维数据压缩技术发展有所裨益。

1 基础理论

1.1 小波变换 小波分析属于时频分析的一种。传统信号分析是建立在傅立叶变换基础上，而小波分析则克服了短时傅立叶变换在单分辨率上的缺陷，具有多分辨率分析的特点，在时域和频域都有表征信号局部信息的能力，时间窗和频率窗都可以根据信号的具体形态动态调整。目前小波已经成为科学研究和工程技术应用中涉及面极其广泛的研究方向。它在数据压缩、信号分析、语音合成、图像识别、计算机视觉、海洋分析等方面的研究取得了有科学意义和应用价值的成果。

小波变换的含义是：把某一被称为基本小波(也叫母小波（motherwavelet)的函数φ(t)作位移b，再在不同尺度a下与待分析信号系统f(x)作内积：

小波变换在频域的等效表示如下：

式中 f(ω)，ψ(ω）分别是 f(ω)，ψ(x)的傅立叶变换。

小波变换具有多分辨率的特点，可以由粗及精逐步观察信号。也可以看成用基本频率特性为ψ(x)的带通滤波器在不同尺度a下对信号作滤波。这组滤波器具有品质因数恒定，即相对带宽(带宽与中心频率之比)恒定的特点。a越大相当于频率越低。适当地选择基本小波，使ψ(x)在时域上为有限支撑，ψ(ω)在频域上也比较集中，便可以使在时频域都具有表征信号局部特征的能力，因此有利于检测信号的瞬态或奇异点。正是由于上述特性，小波变换才被誉为分析信号的数学显微镜。

理论上分析，只要基本小波满足一定容许性条件的均可作为小波变换的母小波。对于不同的要求，应当使用相应的母小波。采用不同的小波对信号进行分析，其效果存在差异，甚至差异较大。选择母小波时一般应具有紧支性、正交性、对称性、正规性、高阶消失矩、理想带通滤波器等特点。

1.2 嵌入式零树小波 基于小波变换的主要编码方法有嵌入式零树小波编码[7](EZW，Embedded ZerotreeWaveletCoding)算法、多级树集合分裂算法(SPIHT，SetPartitioning in Hierarchical Trees)，可逆的嵌入小波压缩法(CREW，Compression with reversible embedded wavelets)等。其中，零树小波编码的成功之处在于合理地利用了零值小波系数具有的零树结构，使得大量树结构的零系数只用一个零树根符号来表示，从而其编码效率大大超过了基于DCT变换的JPEG压缩标准。EZW不仅具有高的压缩比，还满足渐进编解码和算法复杂度低特点。

嵌入式零树小波编码的完整过程如下：1)找出子波系数的最大值，得到最大门限T，作为首次扫描阈值[8]。2)主扫描：按照前述的扫描顺序，用当前阈值分别扫描判别各子像系数的节点类型，最高分辨率子像系数的节点类别只有3类(零树根-ZT、正值-P、负值-N)，此外，其他子像系数的节点类型分为4类(零树根-ZT、正值-P、负值-N、孤立零点-IZ)。将节点类型存入主表。对重要系数的节点，将其绝对值和当前阈值存入副表(阈值作为有效值所在区间的起点)，并将该点的小波系数置为“0”。3)副扫描：所有的子波系数均分类完毕后，用各有效值所在区间的起点加上当前阈值的一半，分别对副表中绝对值进行细化，将其不确定区间减为当前阈值的一半。处在不确定区间高端的有效值编码为“1”，低端的编码为“0”。4)对主表节点类型和副表细化编码进行自适用算术编码输出。5)根据细化后副表中各有效值所在的区间将它们从高到低排序。6)用阈值的一半作为新的当前阈值，重复(2～4)，直到达到所需的比特率和图像质量。

在译码恢复图像的过程中，对系数的恢复也是“一节一节”进行的。首先恢复最重要的系数，再恢复出阈值减半后的控制输出的系数，依次重复，也可以根据图像的质量随时停止译码。例如，译码恢复时，当发现阈值为Tk=t0/2k时，图像效果己很好，则可以抹去其后的码字，保留Tk之前的码字作为压缩代码文件。

EZW算法是针对二维图像，在对一维EEG信号进行小波变换后发现，一维EEG信号的小波域同样存在相互对应的关系。一维信号小波变换后的系数呈金字塔结构，每个较粗尺度上的系数看作父结点，它在较细一尺度对应位置上有两个子结点，而低频系数在下一尺度上只有一个子结点，从而构成一个一维小波系数的树结构。

2 改进EZW算法

小波系数之间具有一定的关联性，可以通过构建小波树结构的方式来加快我们对重要系数的筛选，而在信号压缩中我们要做的就是在一定的压缩比下优先选出最能代表整个信号特征的那些点，所以可以利用小波树的特点来筛选这些点，使筛选出来的这些点能有效的反映整个信号的特征。改进EZW算法描述如下：1)输入压缩倍数和小波系数矩阵，求出压缩后需要的小波系数数据长度。2)找出小波系数的最大值，得到最大门限T，作为首次扫描阈值。3)扫描过程。按照Morton扫描顺序，用当前阈值分别扫描判别各子像系数的节点，对重要系数的节点，将其值和在原矩阵中的位置坐标存入重要系数列表，弱重要系数列表的元素个数达到了所要求的压缩倍数则停止扫描，否则继续扫描，若扫描次序表扫描结束，则将阈值减半后再进入下一次扫描，最终得到的此表就是压缩后的数据。4)还原过程。构造一个与原矩阵大小相同的零矩阵，扫描重要系数列表并根据其各元素在原矩阵中的坐标位置将各元素的值赋予所构造的零矩阵。5)重构过程。赋值完成后，对此矩阵进行小波重构，即得到压缩数据。算法流程如图1。

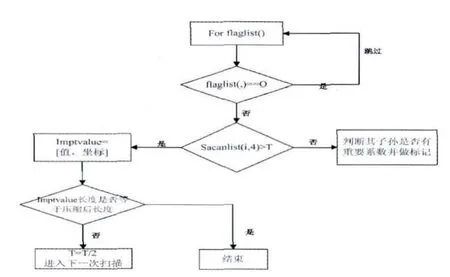
图1 改进EZW算法流程图

3 实例分析

3.1 试验场景 数据来自某医院EEG信号，其系统架构见图2。首先通过传感器采集原始EEG信号，从数据源将源信号以十进制的形式读取出来，以便做进一步分析。然后分析源信号得到采样频率、数据长度、幅值系数及时域信号等所需数据，存入本地数据库。最后当客户端发出请求时，服务器按照设定好的压缩方法对相应数据进行压缩并传输到客户端。本文其研究重点其数据传输过程中的压缩方法。

图2系统结构图

3.2 压缩技术评价指标 评价恢复信号保真度的方法之一就是找出原始信号和重建信号之间的差别。大多数算法采用数字指标，主要原因是数字指标易于定义和计算，无主观因素干扰，能客观地进行比较。压缩比(Compression Ration,CR)是评价压缩效率的常用指标，能较准确地反映压缩前后数据量的变化。

在相同压缩算法情况下，CR的大小受到原始数据采样率、量化精度等影响，有时不能做出很客观的衡量。另一种比较客观的评价方法是恢复后数据占原数据的剩余能量百分比。其中，g(x)为恢复后数据，f(x)为原数据。

3.3 方法对比 为比较三种算法的压缩效果，抽取两组不同测试数据，一组为数据含有较大噪声的EEG信号（简称MN）使用的小波基为bior3.1；另一组为含有较少噪声的EEG信号（简称LN），使用的小波基为db3。用三种方法分别对其进行压缩，结果见表1、2。

表1 对MN信号进行压缩(bior3.1)

表2 对LN信号进行压缩(db3)

通过以上分析可知，对含有较大噪声的EEG信号压缩，在压缩比较大时，改进算法要比小波算法剩余更多的能量，在压缩比较小时，改进算法在剩余能量方面依然优势显著，但在两种情况下其运行时间相对较长，而EZW算法的最大压缩比仅为4，虽然它保存了较多的剩余能量，但其运行时间比起前两种算法长得多。

当对含有较小噪声的EEG信号进行压缩时，三种算法都能对数据进行大幅压缩，在较高压缩比下都保持了较多的剩余能量，但相比较而言，小波算法在时间和剩余能量上都有较大优势，而EZW算法相对效果较差。当进一步加大压缩比后，EZW算法已经无法胜任，小波算法剩余能量下降明显，而改进算法则依然能够保持较高的剩余能量。

分析可知，小波算法时间效率最高，适宜在数据量大，硬件条件有限的情况下使用，而且对噪声小的数据效果更好。改进算法是剩余能量最多，但时间效率相对较低，适宜在数据量不是很大，但对数据精确度要求高的情况下使用，它对不同噪声的数据压缩效果相对来说都不错。EZW算法时间效率和剩余能量相对前两种算法都没有优势，但它确可以得到不同恢复精度的数据，在对压缩比和数据精度要求都不高时可以尝试使用。

本文在研究小波分析和嵌入式零树小波算法的基础上，给出一种改进EZW算法。改进EZW算法能够在保证信号主要特征基本不变的前提下提高其压缩比，减少数据量，改善其存储、传输、检索及分类等问题。改进算法实现简单，运行速度快，可根据需要选择不同的压缩比，对日益发展的一维EEG信号数据的大规模存储和远程传输等有一定的应用价值。对一维信号的压缩算法所做的研究尚处于不断发展中，新的理论、方法会不断涌现。对于小波数据压缩方法而言，如何进一步结合信号特性，提高压缩比等方面，如何找到更加合适的小波基，实现一维信号的近无损压缩有待进一步研究。

[1]Antoniol G,Tonella P.EEG data compression techniques[J].IEEE Transon Biomed Eng,1997,44(2):105-114.

[2]SHI Liying, WANG Youyun. EEG data compression by high- order polynomials approximation [J]. Space Medicine ＆ Medical Engineering,1995,8(4) :168-272.

[3]路淼,周卫东.基于嵌入式零树编码（EZW）的脑电信号压缩算法[J].航天医学与医学工程，2004,17(3）:232-234.

[4]陈仲英,巫斌.小波分析[M].北京:科学出版社,2007.

[5]李良成,刘秋宏,张璟.小波变换在生物医学信号中的应用[J].2008,14(8):24-25.

[6]Shapiro JM. Embedded image coding using zerotrees of wavelet coefficients[J]. IEEE Transactions on Signal Processing,1993,41 (12):3445-3462.

[7]李世雄.小波变换及其应用[M].北京：高等教育出版社,2000.

[8]Rosanna MR. Silveira. A genetic algorithm to compress electrocardiograms using parameterized wavelets[C]. IEEE international symposium on signal processing and information technology,2007.

TP301.6

A

1008-4118（2014）01-0069-04

10.3969/j.issn.1008-4118.2014.01.39

2013-12-27